Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
“Donut-Planeten”
von Isabella
Ich bin 17 Jahre alt und besuche die 8. Klasse (12. Schulstufe) eines Gymnasiums in Salzburg.
Normalerweise sind Planeten rund. Ok – sie sind keine perfekten Kugeln, aber die meisten sind schon sehr nahe dran. Natürlich gibt es auch welche, die stark von der Kugelform abweichen und eine eher elliptische Form angenommen haben. Dennoch würde man spontan wohl kaum an eine andere Form denken. Trotzdem könnte es durchus Planeten geben, die ein bisschen anders aussehen. Sie könnten z.B. noch ein wenig flacher sein als ein elliptischer Planet und ein Loch in der Mitte haben – wie ein Donut.
Man hat zwar noch keinen solchen „Donut-Planeten“ entdeckt (und man wird in naher Zukunft vermutlich auch keine finden), sie könnten aber, rein theoretisch, tatsächlich existieren. (Der mathematisch korrekte Fachbegriff für ein donut-förmiges Objekt lautet übrigens „Torus“.) Um wirklich ein Loch in der Mitte zu bilden benötigt der Planet eigentlich nur eins – eine extrem hohe Rotationsgeschwindigkeit. Die würde dazu führen, dass die sogenannte Zentrifugalkraft (also jene Kraft, die bei einer Drehbewegung nach außen wirkt) die Materie vom Mittelpunk etwas weg drückt und sich ein Loch in der Mitte bildet. Das funktioniert aber nur, wenn die Zentrifugalkraft genau gleich stark ist wie die Gravitation. Wäre sie größer würde der Planet einfach wieder auseinanderfallen. Genauso wenig darf sie auch nicht kleiner sein, da der Planet sonst wieder eine ganz normale Kugelform annehmen würde.
So könnten Planeten auch aussehen. (Urheber Oleg Alexandrov, public domain)
Der „Ring“, also der eigentliche Planet, kann dabei aber nicht beliebig groß werden. Ein Torus hat zwei Radien. Einen „major Radius“ R und einen „minor Radius“ r. Dabei muss major Radius / minor Radius < 3 sein. Ist es größer als 3, dann wäre der Planet unstabil und würde zerbrechen.
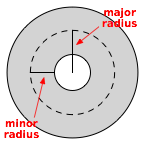
Torus mit eingezeichneten Radien (Urheber Jamis Buck, Creative Commons BY 4.0)
Auf einem solchen Planeten gäbe es zwei Äquatoren. Einen inneren, welcher dem Umfang des Lochs entspricht, und einen äußeren, der den Umfang des eigentlichen Planeten darstellt. Geht man von einem Planeten aus, der die gleiche Masse wie unsere Erde hätte, dann wäre die Gravitation an den Äquatoren mit 0,3 g am schwächsten und an den Polen mit 0,65 g am stärksten. Das ist zwar an beiden Stellen weniger als auf der Erde, entspricht aber einem Unterschied von 216%. Unser Gewicht wäre also stark davon abhängig wo genau wir uns befinden.
Durch die enorm hohe Rotationsgeschwindigkeit würde ein Tag nur mehr ein paar Stunden dauern. Dennoch hängt auch viel von der Stärke der Achsenneigung ab. Geht man davon aus, dass der Planet nicht geneigt ist, würde kein Licht in den inneren Kreis vordringen. Beim inneren Äquator wäre es somit immer dunkel. An den Polen wäre die Sonne am Horizont sichtbar und ein kleines Stückchen näher am inneren Äquator herrscht ständige Dämmerung. Am äußeren Äquator hingegen würde sich ein „Donut-Planet“ nicht von unserer Erde unterscheiden. (Außer natürlich durch die Tageslänge.)
Geht man aber von der gleichen Achsenneigung wie bei unserer Erde aus, also ca. 23 Grad, dann ändert sich die Situation ein wenig. Im Frühling und Herbst würde sich nicht viel verändern. Am inneren Äquator wäre es immer noch ständig dunkel, am äußeren Äquator hingehen bleibt der Tag-Nacht-Rhythmus ganz normal bestehen. Im Sommer und im Winter sieht die Sache jedoch ein wenig anders aus. Dann kommt das Licht nämlich bis zum inneren Äquator. Aber natürlich nur auf die Seite, die ein Stückchen weiter von der Sonne entfernt ist. Die andere Seite wäre ja von der Sonne abgewandt. Wenn der Planet eine ähnliche Atmosphäre wie unsere Erde hätte, dann wäre diese Seite aber trotzdem nicht ganz dunkel. Wenn das Licht die Atmosphäre durchdringt, wird es dabei gebrochen und somit kann das gesamte Loch ein wenig ausgeleuchtet werden. Dadurch wird diese Seite zwar nicht besonders hell, sie bleibt aber auch nicht komplett dunkel. An den Polen würde die Sonne für ein halbes Jahr nicht untergehen und danach würde sie für ein halbes Jahr nicht aufgehen.
Viele Planeten haben einen oder sogar mehrere Monde. Ein „Donut-Planet“ wäre ebenfalls dazu in der Lage einen Mond in einer Umlaufbahn zu halten. Es gäbe sogar mehr als nur eine Möglichkeit für das Aussehen der Bahn. Eine Möglichkeit wäre z.B. eine ganz normale elliptische Umlaufbahn.
Aber durch das Loch in der Mitte ergeben sich noch ganz andere Möglichkeiten für eine Umlaufbahn. Eine etwas andere Variante wäre eine Bahn direkt durch das Loch. Doch dazu gibt es auch wieder verschiedene Möglichkeiten. Eine davon wäre eine gerade Linie, an der sich der Mond einfach auf und ab bewegt. Die Linie muss nicht mal gerade sein. Sie könnte genauso gut eine kleine Biegung aufweisen. Wenn sich der Mond dann auch noch in dem Loch dreht, (nicht um seine eigene Achse, sondern in einer Kreisbewegung das Loch quasi „umkreist“) dann würde die Bahn aussehen wie ein Hyperboloid.
Eine Umlaufbahn in Form einer Acht, wäre theoretisch natürlich auch möglich. Dabei würde sich der Mond zuerst durch das Loch bewegen. Dann würde er eine Seite des Planeten umrunden und sich wieder durch das Loch bewegen. Anschließend würde er die andere Seite umrunden und wäre somit wieder an seiner Ausgangsposition. Dreht er sich dabei auch noch um den Planeten herum, dann würde die Bahn wie eine Hülle um den Planeten aussehen.
Wir werden dennoch in naher Zukunft wohl kaum solche „Donut-Planeten“ finden. Die Wahrscheinlichkeit, dass sie überhaupt existieren ist verschwindend gering, aber trotzdem sind sie nicht unmöglich.
Verwendete Quellen
Kommentare (68)