 Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Newtons „Opticks“ – ein bahnbrechendes Werk der Physik
von Lercherl
Ich habe Chemie und Physik studiert, beschäftige mich beruflich mit Supercomputing und privat mit allem möglichem, mit Vorliebe aber mit Wissenschaftsgeschichte. Ich bin ein großer Fan des Internet Archive, das zahllose Klassiker der Wissenschaft zugänglich macht. Ich kann ziemlich wenig mit Science Fiction anfangen und kann Star Trek und Star Wars nicht auseinanderhalten.
Mehr als hundert Jahre nach Newtons Werk zur Optik erschien Goethes „Farbenlehre“, in der Goethe Newtons Theorie zur Farbentstehung heftig angreift und seine eigene Lehre propagiert. Von der Mehrzahl der Forscher wird Goethes Farbenlehre heute für weitgehend wertlos für die Erklärung der Farbentstehung gehalten. Eine Minderheit ist aber der Meinung, dass Goethes Farbenlehre auch tiefe Einsichten enthält, die Newton verborgen geblieben sind. Ursprünglich wollte ich in diesem Artikel Newtons und Goethes Theorien gegenüberstellen, aber beim Schreiben ist der Teil über Newton immer mehr angewachsen, sodass das Material über Newton alleine für einen Blogartikel mehr als ausreicht. Vielleicht schreibe ich später noch einen Artikel über Goethe und seine Farbenlehre, und einen dritten mit einer Gegenüberstellung der beiden, so wie Plutarch in seinen Parallelbiographien: Demosthenes. Cicero. Vergleich Demosthenes-Cicero.
Newtons Werk trägt den etwas sperrigen Titel „Opticks: or, a Treatise of the Reflections, Refractions, Inflections and Colours of Light,“ es wird meist kurz als Opticks bezeichnet. Dieser langatmige Titel beschreibt recht genau, worum es primär geht: um Spiegelung, Brechung und Beugung als die wesentlichen Mechanismen der Entstehung von Farberscheinungen. Die erste Ausgabe der Opticks erschien 1704, es folgten später noch eine lateinische Ausgabe in der Übersetzung von Samuel Clarke (1706) und mehrere überarbeitete englische Ausgaben, die vierte Ausgabe, die ich im Folgenden zitiere, erschien postum 1730. Mit passablen Englischkenntnissen und Grundkenntnissen der Physik sind die Opticks auch heute noch relativ flüssig zu lesen, sobald man sich an das umständliche und antiquierte Englisch und die ungewohnte Nomenklatur gewöhnt hat. Ganz anders die 1687 erschienenen Principia mathematica: die wurden auf Latein verfasst und verlangen mit ihrer anspruchsvollen Mathematik den Lesern Einiges ab. Eine deutsche Übersetzung der Opticks von William Abendroth erschien 1898 als Band 96 und 97 von Ostwalds Klassikern der exakten Wissenschaften.
Euklid und Newton
Wer die Opticks liest, dem fällt sofort auf, dass Newton sich im Aufbau an Euklids Elementen orientiert hat. Natürlich nur, wenn er oder sie die Elemente kennt. Wer sie nicht kennt, sollte sie unbedingt kennenlernen, finde ich. Sie sind beispielsweise hier, hier und hier zu finden, oder auch hier: letztere Ausgabe ist für das heutige Publikum wohl schwerer zu verstehen, aber das Buch ist unvergleichlich schöner. Ich hätte sehr gern ein Exemplar davon – auch wenn ich schon eine schöne Euklid-Ausgabe besitze, nämlich diese hier:
Es ist anzunehmen, dass Newton diese Ausgabe gekannt hat, sie erschien 1703, ein Jahr vor den Opticks. Auch war er mit dem Herausgeber, dem schottischen Mathematiker David Gregory befreundet – sofern Newton überhaupt je mit jemandem befreundet war; jedenfalls ist nicht überliefert, dass die beiden gestritten hätten. Für die Opticks hat er diese Ausgabe aber wohl nicht benutzt, seine Arbeiten zur Optik erfolgten schon viel früher.
Mit Euklid hat sich Newton kein schlechtes Vorbild ausgesucht. Euklid, der Vater der mathematischen Strenge, beginnt mit Definitionen (Punkt, Gerade, Kreis usw.) und Axiomen, den nicht beweisbaren, als wahr angenommenen Grundsätzen. Der Rest des Buches besteht ausschließlich aus einer Reihe von Sätzen (Theoremen) und Aufgaben. Ein Satz ist beispielsweise: „In jedem Dreieck ist die Summe zweier beliebiger Winkel weniger als zwei rechte Winkel“ (I.17). Nach jedem Satz folgt der Beweis: Aus den Axiomen und vorher bewiesenen Sätzen wird Schritt für Schritt der zu beweisende Satz hergeleitet. Jeder Beweis schließt mit den Worten: „was zu beweisen war“, auch in der lateinischen Form „quod erat demonstrandum“, abgekürzt q.e.d., bekannt, obwohl Euklid natürlich griechisch schrieb: ὅπερ ἔδει δεῖξαι. Ein Beispiel einer Aufgabe ist „In einen Kreis ein gleichseitiges und gleichwinkeliges Fünfeck einschreiben“ (IV.11). In ähnlicher Weise werden die einzelnen Konstruktionsschritte hergeleitet, bis die Aufgabe fertiggestellt ist, die Konstruktion schließt mit dem weniger bekannten „quod erat faciendum“ (was zu tun war).

Euklids Konstruktion des regelmäßigen Fünfecks. Diese Übersetzung aus dem 12. Jahrhundert des Adelard von Bath verwendet die Formulierung „hoc est quod proposuimus“ statt „quod erat demonstrandum“.
Newtons Opticks, genauer gesagt, das erste Buch der Opticks, sind formal genau so aufgebaut wie die Elemente: am Anfang Definitionen und Axiome, dann nacheinander Satz/Beweis, Satz/Beweis, Aufgabe/Lösung usw. Was er als „Axiome“ bezeichnet, sind Sätze aus der geometrischen Optik, beispielsweise das Axiom I: The Angles of Reflexion and Refraction lie in one and the same Plane with the Angle of Incidence. Dass Newton diese Sätze als Axiome einführt, kann man durchaus kritisieren: Sie müssen nicht von vornherein als wahr angenommen werden, sie lassen sich ohne weiteres experimentell verifizieren. Anscheinend wollte Newton mit geometrischer Optik, um die es in diesem Buch nicht vorrangig geht, keine Zeit verlieren und sie als bekannt voraussetzen: I have now given in Axioms and their Explications the sum of what hath hitherto been treated of in Opticks. Bei den Erläuterungen zu Axiom VII gibt Newton auch eine im Wesentlichen korrekte Erklärung über das menschliche Sehvermögen: When a Man views any Object […] the Light which comes from the several Points of the Object is so refracted […] as to converge […] in the bottom of the Eye, and there to paint the Picture of the Object. And these Pictures, propagated by Motion along the Fibres of the Optick Nerves into the Brain, are the cause of Vision.
Bei den zu beweisenden Sätzen gibt es aber einen wesentlichen Unterschied zu Euklid: Der „Beweis“ erfolgt durch Experimente. Newton beschäftigt sich mit Physik und Euklid mit Mathematik: an einem korrekten mathematischen Beweis ist nicht zu rütteln; dass es unendlich viele Primzahlen gibt, wie Euklid im Satz IX.20 bewiesen hat, ist unumstößlich und kann durch keine wie auch immer geartete neue Erkenntnis widerlegt werden. In der Physik gibt es hingegen keine solchen Beweise, wenn ein physikalisches Gesetz auch durch noch so viele Experimente und Beobachtungen untermauert ist, kann uns die Natur immer noch ein Schnippchen schlagen und uns zeigen, dass unter speziellen Umständen das Gesetz nicht gilt. In Newtons Ankündigung „The Proof by Experiments“ ist das Wort „Beweis“ daher nicht als mathematischer Beweis zu verstehen. Er schreibt dazu am Ende des dritten Buches: And although the arguing from Experiments and Observations by Induction be no Demonstration of general Conclusions; yet it is the best way of arguing which the Nature of Things admits of […].
Eine solche Art von Beweis war zu Newtons Zeit noch recht neu, und es galt, manche Vorbehalte gegenüber einem experimentellen Zugang und festgefahrene Denkweisen, die teils noch aus der Antike übernommen wurden, zu überwinden. Die euklidische Strenge hat der griechischen Mathematik zu ihrer Blüte verholfen, aber ihre unkritische Anwendung auf die Physik hat mehr Schaden als Nutzen angerichtet. Aristarch von Samos beispielsweise berechnete das Verhältnis der Abstände von Sonne und Mond zur Erde. Seine mathematische Methode ist absolut korrekt, trotzdem kommt er zu vollkommen falschen Zahlen (zwischen 18 und 20, der wahre Wert liegt nahe bei 400), weil seine verwendeten Messwerte ungenau sind. Alle beobachteten und experimentell ermittelten Größen formuliert er als „Hypothesen“ und verliert kein Wort darüber, wie er darauf kommt.
Das erste Buch: Auf Spiegeln und Brechen
Zurück zu Newtons Opticks. Das erste Buch enthält, in zwei Teile gegliedert, insgesamt 19 „Propositions“, davon sind elf Sätze (Theorems) und acht zu lösende Probleme. Von den Sätzen möchte ich hier die wichtigsten im Wortlaut wiedergeben. In Teil I:
Theor. I. Lights which differ in Colour, differ also in Degrees of Refrangibility.
Heute bezeichnet man diesen Effekt, d.h. die Abhängigkeit des Brechungsindex von der Farbe (Wellenlänge) als Dispersion. Die Stärke der Dispersion hängt vom Material ab.
Theor. II. The Light of the Sun consists of Rays differently Refrangible.
Newton verwendet viel Mühe auf den experimentellen Beweis dieses Satzes: auf mehr als 30 Seiten beschreibt er 10 Experimente.
Theor. VI. The Perfection of Telescopes is impeded by the different Refrangibility of the Rays of Light.
Dieser Satz ist zwar nicht essentiell für die Theorie, aber er gibt einen Einblick in die Motivation Newtons, sich mit Optik und vor allem mit Farberscheinungen zu beschäftigen: er hat sich über die Unzulänglichkeiten der damaligen Teleskope geärgert. Dieser Ärger brachte ihn dazu, ein Spiegelteleskop zu erfinden, den Newton-Reflektor: Seeing therefore the Improvement of Telescopes of given lengths by Refractions is desperate, I contrived heretofore a Perspective by Reflexion, using instead of an Object-glass a concave Metal. So verzweifelt wie Newton sind wir heute nicht: im 18. Jahrhundert wurde entdeckt, dass durch geeignete Abfolge von Gläsern mit unterschiedlichen Dispersionseigenschaften (Flint- und Krongläser) die chromatische Aberration und andere Linsenfehler recht gut kompensiert werden können.
Unter den Sätzen in Teil II des ersten Buches finden sich:
Theor. II. All homogeneal Light has its proper Colour answering to its Degree of Refrangibility and that Colour cannot be changed by Reflexions and Refractions.
In moderner Sprache formuliert: monochromatisches Licht hat eine wohldefinierte Wellenlänge und damit eine wohldefinierte Farbe, die sich durch Spiegelung und Brechung nicht ändert. Geneinsam mit Theorem II aus dem I. Teil ist dieser Satz die wichtigste Erkenntnis Newtons zur Theorie der Farbentstehung. Verschiedene Materialien erscheinen uns in unterschiedlichen Farben, weil sie die einfallenden Lichtstrahlen je nach Farbe unterschiedlich stark reflektieren.
Heute kennen wir einige Effekte, die dennoch die Wellenlänge monochromatischen Lichts ändern können, etwa den Doppler-Effekt oder inelastische Streuung (Raman-Streuung).
Theor. III. Colours may be produced by Composition which shall be like to the Colours of homogeneal Light as to the Appearance of Colour but not as to the Immutability of Colour and Constitution of Light. […]
Eine Begründung für dieses Phänomen kann nur die Physiologie liefern, nicht die Physik: es besteht kein physikalischer Grund, warum etwa gelbes Licht dasselbe sein sollte wie eine Mischung aus Rot und Grün. Das menschliche Auge kann keinen Unterschied zu erkennen, weil es für den gesamten Wellenlängenbereich nur über drei Farbrezeptoren verfügt, die von gelbem und gemischt rot-grünem Licht in gleicher Weise angeregt werden. Das war zu Newtons Zeit noch nicht bekannt. Newton stellt richtig fest, dass es sehr wohl Unterschiede in der „Beschaffenheit“ des Lichts geben kann, auch wenn kein Farbunterschied ersichtlich ist: so kann gelb erscheinendes Licht mit einem Prisma in seine roten und grünen Bestandteile zerlegt werden, sofern es aus solchen Teilen besteht, nicht aber monochromatisches gelbes Licht.
Theor. V. All the Colours in the Universe which are made by Lights and depend not on the Power of Imagination are either the Colours of homogeneal Lights or compounded of these […].
Heute würden wir diese Erkenntnis vielleicht so formulieren: Jede elektromagnetische Welle ist durch die Abhängigkeit der Intensität I von der Wellenlänge λ charakterisiert; die Funktion I(λ) im sichtbaren Bereich bestimmt, welche Farbempfindung dadurch im menschlichen Auge ausgelöst wird.
Das zweite Buch: Farben in dünnen Schichten
Dünne Schichten, etwa Seifenblasen oder Ölfilme auf Wasser, schillern in allen Farben des Regenbogens. Newtons Theorie der Farbentstehung aus Buch I kann diese Farben nicht erklären. Heute wissen wir, dass es sich dabei um Interferenzerscheinungen handelt: Licht, das am oberen Rand reflektiert wird, interferiert mit den Reflektionen vom unteren Rand: sind die beiden Lichtstrahlen „in Phase“, so ist die Interferenz „konstruktiv“; ist die Phasendifferenz hingegen gleich der halben Wellenlänge, so kommt es zu „destruktiver Interferenz“, und die beiden Strahlen löschen einander aus.
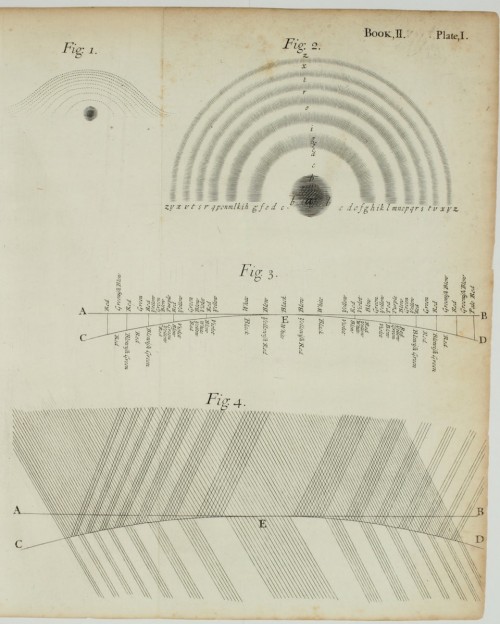
Newton untersuchte Farben an dünnen Schichten mit Hilfe zweier aneinandergepresster Linsen, von denen die obere unten flach ist, die untere eine sphärische Oberfläche mit sehr großem Radius hat. Mit dieser Versuchsanordnung hat er eine dünne Luftschicht zwischen den beiden Linsen, deren Dicke mit dem Abstand vom Mittelpunkt zunimmt und sich aus diesem Abstand und dem Radius der sphärischen Linse berechnen lässt. Um den Mittelpunkt erscheint eine Abfolge farbiger Ringe, die heute noch als Newton’sche Ringe bekannt sind. Newton illustriert seine Experimente mit folgender Zeichnung:
Er beschreibt die beobachteten Phänomene als eine Abfolge von „Fits of easy Reflexion“ und „Fits of easy Transmission“. Was er genau mit „Fit“ meint, lässt sich schwer ausmachen, das Wort ist außerordentlich vieldeutig. Abendroth übersetzt es mit „Anwandlung“. Dass es keine besonders zufriedenstellende Theorie ist, abwechselnde Helligkeit und Dunkelheit darauf zurückzuführen, dass das Licht gerade solche Anwandlungen hat, ist wohl auch Newton selber aufgefallen. Man möchte fast meinen, er vermeidet mit Gewalt das Wort „Welle“ – was würde eine periodische Abfolge von Licht und Dunkelheit besser beschreiben als eine Welle? Newton hatte dafür seine Gründe, gute Gründe und auch weniger gute. Zu den guten Gründen zählte, dass Wellenphänomene seiner Korpuskulartheorie zu widersprechen schienen. Erst mit dem Welle-Teilchen-Dualismus der Quantenmechanik wurde im 20. Jahrhundert gezeigt, dass diese beiden Betrachtungsweisen einander nicht ausschließen, sondern ergänzen. Das konnte Newton natürlich nicht wissen. Auch heute fällt es uns sehr schwer, diesen Dualismus zu verstehen: „Verständnis“ bedeutet eher, dass wir uns schon daran gewöhnt haben. Zu den weniger guten Gründen zählte, dass Erklärungen von Licht als Wellenphänomenen von seinen Konkurrenten Robert Hooke und Christiaan Huygens stammten – und so etwas konnte Newton nicht anerkennen.
Im Gegensatz zum ersten Buch präsentiert das zweite keine Theorie nach dem euklidischen Schema von Satz und Beweis. Die große Leistung liegt hier weniger in einer schlüssigen Theorie, sondern in der Sorgfalt seiner Experimente und in der Genauigkeit seiner Messungen. Diese Genauigkeit möchte ich an einem einzigen Beispiel illustrieren, nämlich Proposition XVIII:
If the Rays which paint the Colour in the Confine of yellow and orange pass perpendicularly out of any Medium into Air, the Fits of easy Reflexion are the 1/89000th part of an Inch. In moderne Sprache übersetzt und in SI-Einheiten umgerechnet bedeutet das: die halbe Wellenlänge von gelb-orangem Licht beträgt 285 nm. In Wahrheit entspricht eine Wellenlänge von 2*285 = 570 nm rein gelbem Licht: Newtons Messfehler beträgt daher nur wenige Nanometer.
Buch 3: Beugen und Fragen
Bis hierher hat Newton noch kein Wort über Beugung verloren, obwohl Beugung („Inflexion“) im Titel seines Werkes vorkommt. In einem relativ kurzen Abschnitt beschreibt Newton einige Experimente zu Beugungserscheinungen. Der interessantere – und auch längere – Teil von Buch 3 enthält eine lange Liste von Fragen zur Optik, zu denen Newton keine Antwort hat: I shall conclude with proposing only some Queries, in order to a farther search to be made by others. Ich zitiere hier einige der interessantesten Fragen:
Qu. 5. Do not Bodies and Light act mutually upon one another; that is to say, Bodies upon Light in emitting, reflecting, refracting and inflecting it, and Light upon Bodies for heating them, and putting their parts into a vibrating motion wherein heat consists?
Qu. 8. Do not all fix’d Bodies, when heated beyond a certain degree, emit Light and shine and is not this Emission perform’d by the vibrating motions of their parts
Qu. 25. Are there not other original Properties of the Rays of Light, besides those already described?
Qu. 26. Have not the Rays of Light several sides, endued with several original Properties?
Qu. 29. Are not the Rays of Light very small Bodies emitted from shining Substances?
Qu. 30. Are not gross Bodies and Light convertible into one another, and may not Bodies receive much of their Activity from the Particles of Light which enter their Composition?
Nr. 5 und 8 sind Fragestellungen zur Theorie der Wärmestrahlung, die im 19. Jahrhundert weiterentwickelt wurde (Wien’sches Verschiebungsgesetz, Stefan-Boltzmann-Gesetz) und im Jahr 1900 durch Max Planck ihre heutige Form erhielt; Planck legte damit den Grundstein zur Quantentheorie.
Nr. 25 und 26 sind durch das Phänomen der Doppelbrechung, für die Newton keine Erklärung hat, begründet. Die unbekannte Eigenschaft des Lichtes, die diesen Effekt verursacht, ist die Polarisation, wie wir heute wissen.
Nr. 29 und 30 sind tiefgründige Fragen zur Natur von Licht und Materie und ihrer Wechselwirkungen, auf die erst die Quantenmechanik einigermaßen zufriedenstellende Antworten geben kann.
Newtons „Regulae philosophandi“
Am Ende des dritten Buches findet sich ein interessanter Abschnitt zur Erkenntnistheorie, von dem ich oben im Abschnitt über experimentelle Beweise einen Ausschnitt zitiert habe. Seine Grundsätze der Erkenntnistheorie hat Newton schon in den Principia mathematica als Regulae philosphandi formuliert, was man nicht als „Regeln des Philosophierens“ übersetzen sollte. Newtons „Naturphilosophie“ ist Naturforschung im weiteren und Physik im engeren Sinn. Ich habe ja das Glück, eine schöne Ausgabe der Principia zu besitzen:
Diese sogenannte „Jesuitenausgabe“ wurde 1760 in Genf von Thomas Le Seur und François Jacquier veröffentlicht, ein irreführender Name, denn die Herausgeber waren beide Franziskaner. Sie bringen ausführliche Erklärungen und Erläuterungen, die in Summe wesentlich länger sind als Newtons Text. Newton hat sich wohl im Grab umgedreht, denn sie verwenden die Nomenklatur des verhassten Leibniz. Vor dem dritten Buch schreiben sie, dass sie jetzt so tun müssen, als glaubten sie, dass sich die Erde bewegt – aber sie befolgen in dieser Frage gewiss die Anweisungen des Papstes.
Aber zurück zu Newtons Regeln, ich will hier ja nicht mit meinen schönen Büchern angeben (oder nur ein wenig). Ich widerstehe der Versuchung, die Regeln im lateinischen Original zu zitieren und bringe daher die etwas hölzerne Übersetzung von Jakob Philipp Wolfers:
Regeln zur Erforschung der Natur
1. Regel. An Ursachen zur Erklärung natürlicher Dinge nicht mehr zuzulassen, als wahr sind und zur Erklärung jener Erscheinungen ausreichen.
Diese Regel ist das Sparsamkeitsprinzip, einer der wichtigsten Grundsätze der Wissenschaftstheorie. Es ist auch als Ockhams Rasiermesser bekannt und hat eine lange Geschichte seit der Scholastik.
2. Regel. Man muss daher, so weit es angeht, gleichartigen Wirkungen dieselben Ursachen zuschreiben.
Diese Regel ist ein Sonderfall der ersten: Es ist die einfachste und plausibelste Annahme, die beibehalten werden soll, solange nicht gewichtige Gründe dagegensprechen.
3. Regel. Diejenigen Eigenschaften der Körper, welche weder verstärkt noch vermindert werden können und welche allen Körpern zukommen, an denen man Versuche anstellen kann, muss man für Eigenschaften aller Körper halten.
Hier muss man wohl ein bisschen grübeln, was gemeint ist: Newtons Motivation für diese Regel sind hauptsächlich Himmelskörper, mit denen man nicht so leicht Versuche anstellen kann. Unveränderliche Eigenschaften irdischer Körper (etwa Trägheit), gelten wohl auch für Himmelskörper.
4. Regel. In der Experimentalphysik muss man die, aus den Erscheinungen durch Induction geschlossenen, Sätze, wenn nicht entgegengesetzte Voraussetzungen vorhanden sind, entweder genau oder sehr nahe für wahr halten, bis andere Erscheinungen eintreten, durch welche sie entweder grössere Genauigkeit erlangen, oder Ausnahmen unterworfen werden.
Trotz der umständlichen Formulierung ist hier klar, worum es geht: aus Einzelbeobachtungen kann man durch Verallgemeinerung physikalische Gesetze formulieren. Die gelten so lange, bis sie aufgrund weiterer Beobachtungen verfeinert oder modifiziert werden müssen. Newton war nicht der erste und einzige, der so einen Grundsatz verfochten hat, aber er hat wesentlich dazu beigetragen, dass Beobachtung und Experiment die gebührende Wertschätzung erfuhren. Viele gelehrte Diskussionen wurden damals ausschließlich von abstrakten Grundsätzen ausgehend geführt und verloren so leicht den Bezug zur Realität.
Fazit
Obwohl Newtons Beschäftigung mit Optik nur ein Nebenprodukt seiner astronomischen Forschungen war und das Buch manchmal etwas unfertig wirkt, sind die Opticks ein bahnbrechendes Meisterwerk:
1. Newton gelingt es, eine einfache und konsistente Theorie der Entstehung von Farben durch Brechung und Spiegelung zu formulieren. Diese Theorie wird durch eine große Zahl an Beobachtungen und Experimenten gestützt. Die Beschreibungen der Experimente sind so detailliert und ausführlich, dass sie nachvollzogen werden können.
2. Er beschreibt sorgfältige Beobachtungen an Farberscheinungen durch Beugung und Interferenz (nach moderner Sprachweise), für die er Erklärungsmöglichkeiten, aber keine konsistente Theorie anbietet.
3. Er wendet konsequent wissenschaftstheoretische Prinzipien an, wie er sie in den Principia mathematica formuliert hatte. Diese Prinzipien zeichnen auch heute noch gute wissenschaftliche Praxis aus.
4. Er erkennt offen an, welche Phänomene er nicht erklären kann und formuliert offene Punkte als Fragen, die noch weiter erforscht werden müssen und weist damit der weiteren Forschung den Weg.













Kommentare (18)