Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Der Kampf des (19.) Jahrhunderts
von MZ
Ich bin gelernter Hadronenphysiker und zur Zeit in der industriellen Forschung tätig. Dies ist mein erster populärwissenschaftlicher Text, mit dem ich testen will, ob mir wissenschaftliches Schreiben Spaß macht. Tut es.
Wie ist eigentlich Vektorrechnung entstanden? Was waren die Vorraussetzungen und die historischen Umstände? Was haben Quaternionen damit zu tun?
Stellt euch vor, ihr seid Raumfahrer (oder wenigstens Raumfahrtingenieur) und möchtet mit einem Raumfahrzeug einen Asteroiden besuchen. Dazu müsst ihr wissen, wo das Gefährt relativ zum Asteroiden ist und wie ihr es ausrichten müsst, damit es am Ziel ankommt. Oder ihr seid Grafikentwickler und wollt ein Computerspiel mit 3D-Grafik basteln. Das funktioniert nur, wenn die Objekte im Spiel sich korrekt bewegen und drehen, nachdem der Spieler z.B. die Maus bewegt und damit die Sichtperpektive ändert. Auch der Automobilentwickler braucht ein gutes Verständnis von Position und Orientierung von Objekten in der Ebene und im Raum, wenn er selbstfahrende Autos entwickelt.
Den Ort eines Objekts kann man ja mit der x-, y- und z-Koordinate angeben, aber wie sieht das mit der Richtung aus? Beim Auto kann man zum Beispiel sagen, es fährt Richtung Nordwesten. Beim Raumgefährt und bei den Computerspielobjekten reicht das aber nicht, weil diese noch einen Winkel gegen die Horizontale und um die eigene Längsachse haben können. Eine Möglichkeit ist die Angabe von Euler-Winkeln. Es gibt unterschiedliche Systeme von Euler-Winkeln, aber einer gängigen Konvention nach nennt man die drei Winkel Roll-, Gier- und Nickwinkel. Eine Benennung, die ganz gut mit der Anschauung zusammenpasst.
Dann gibt es aber auch Menschen, die Stein auf Bein schwören, dass Quaternionen heutzutage das Wundermittel sind, Rotationen im Raum zu beschreiben. Als ich darüber gelesen habe, war ich erstaunt. Quaternion? Das ist doch eine Erweiterung der komplexen Zahlen, die im vor- oder vorvorletzten Jahrhundert gefunden wurden. Und jetzt sind die wieder ausgegraben worden und vollbringen wundersame Dinge in mathematischen Anwendungen? Toll! Aber irgendwie fand ich das merkwürdig. Ist das wirklich so eine tolle Erkenntnis, dass ein in die Tage gekommenes, staubiges Zahlensystem besser geeignet ist, Rotationen im Raum zu beschreiben als Winkel, sprich Drehmatrizen, sprich “moderne” lineare Algebra?
Quaternionen sind zu einer Zeit entstanden, in der auch die Theorie der Elektrodynamik entstand. Die Grundgleichungen der E-Dynamik wurden von James Clerk Maxwell in den 1860er Jahren entwickelt und veröffentlicht (und heißen heute Maxwell-Gleichungen). Diese Gleichungen, sowie die ganze Theorie der E-Dynamik basiert auf dem Rechnen mit Vektoren, mathematische Objekte, die in den 1880er Jahren entstanden. Richtig gelesen: Da stimmt schon wieder was nicht mit der zeitlichen Abfolge der Dinge! Was ist denn historisch tatsächlich passiert? Weil ich neugierig war, habe ich mir ein Buch gekauft und bin der Sache nachgegangen.
Der Status quo im Jahr 1830
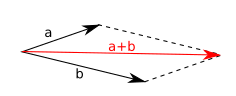
In den Jahrzehnten um und vor 1830 waren die Mathematiker bemüht, den drei-dimensionalen Raum zu beschreiben. Aus heutiger Sicht suchte man damals die Mathematik der Vektoren. Man kannte nur “einfache” Zahlen. Drei Zahlen sind nötig, um eine Position im Raum anzugeben, aber wie verhalten sich verschiedene Positionen, also Punkte, zueinander? Wie können Linien, Flächen, Räume beschrieben und erzeugt werden, die beliebig orientiert sind? Bekannt waren damals schon ein paar Eigenschaften, die diese neue Mathematik haben musste. Unter anderem von Isaac Newton war die Idee des Kräfteparallelograms bekannt.
Kräfteparallelogramm zur Addition zweier Kräfte.
Im Gegensatz zu einer zahlenartigen Größe hat eine Kraft nicht nur einen Betrag sondern auch eine Richtung. Hat man zwei Kräfte, die an einem Körper zerren, dann passiert das Gleiche, wie wenn nur eine Kraft wirkt, deren Betrag und Richtung der Diagonalen des von den beiden Kräften aufgespannten Parallelograms entspricht. Aus heutiger Sicht beschreibt das haargenau die Addition von zwei Vektoren. Bezüglich Linien, Flächen und Räume hatte man folgende Idee: Eine Linie, im heutigen Sprachgebrauch Strecke, ist charakterisiert durch zwei Punkte. Zwei Strecken, die nicht parallel sind und die einen gemeinsamen Punkt haben, spannen ein Parallelogramm auf, dessen Flächeninhalt entweder durch den Winkel oder mit den Koordinaten der Punkte berechnet werden kann. Das wird heute auch noch so gemacht und entspricht dem Kreuzprodukt zweier Vektoren. Im damaligen Bild hat man also zwei Linien multipliziert und bekam dabei eine Fläche. Der logisch nächste Schritt ist es, noch eine Linie an diese Fläche zu multiplizieren und ein Volumen zu bekommen (ein Parallelepiped, aufgespannt durch die drei Vektoren).
Strecke mal Strecke ergibt Fläche, Fläche mal Strecke ergibt Volumen.
Die Strategie bei der Suche der drei-dimensionalen Algebra war eine Verallgemeinerung der Rechnerei im zwei-dimensionalen. Die war nämlich damals schon bekannt. Komplexe Zahlen waren seit dem 16. Jahrhundert bekannt und 1799 wurde von Caspar Wessel ein “Paper” veröffentlicht, in dem beschrieben ist, dass sich komplexe Zahlen prima eignen, geometrische Vektoren in der Ebene, also in 2D, zu beschreiben, inklusive Addition, Subtraktion, Multiplikation und Division. Über dieses Thema gab es letztes Jahr hier beim Schreibwettbewerb einen sehr guten Überblick. Ausgehend von der 2D-Darstellung suchte man (unter anderem der große Carl Friedrich Gauss) eine Erweiterung der komplexen Zahlen, um damit im 3D zu rechnen – und scheiterte. Heute weiß man, dass so eine Verallgemeinerung von 2D auf 3D, die die reellen und komplexen Zahlen als Grenzfall enthält, nicht funktionieren kann.
Hamilton und Grassmann
Die weitere Geschichte der Vektoren wird zunächst von zwei sehr interessanten und unterschiedlichen Persönlichkeiten bestimmt. Fangen wir mit William Rowan Hamilton an. Hamilton wurde 1805 in Dublin, Irland geboren und war ein echtes Wunderkind. Mit 13 Jahren konnte er 13 unterschiedliche Sprachen sprechen. Während seiner Studienzeit ist er vielfach ausgezeichnet worden und noch vor seinem Abschluss ist er mit 21 Jahren zum Professor für Astronomie und zum königlichen Astronom von Irland ernannt worden. Mit 30 ist er zum Ritter geschlagen worden und war einer der berühmtesten Mathematiker seiner Zeit. Auch Hamilton hatte zunächst erfolglos nach den 3-dimensionalen Zahlen gesucht, dann aber 1843 die Quaternionen entdeckt.
Quaternionen sind vier-dimensionale Zahlen. Während komplexe Zahlen neben der reellen Zahl noch eine imaginäre Einheit besitzen (i), haben Quaternionen eine reelle Zahl und gleich drei imaginäre Einheiten (i, j, k). Ein Quaternion x sieht also so aus:
x = (x0, x1, x2, x3) = x0+i·x1+j·x2+k·x3
Man kann mit diesen Zahlen “ganz normal” rechnen und sie als Gleichung mit drei Unbekannten i, j und k betrachten. Jedes mal, wenn man ein Produkt zweier dieser Unbekannten hat, kann man es nach folgenden Regeln ersetzen (um dadurch nur Terme mit höchstens einer Unbekannten zu bekommen):
i·i = j·j = k·k = -1
i·j = -i·j = k, j·k = -k·j = i, k·i = -i·k = j
Was hat das Ganze jetzt mit Vektoren zu tun? Nun, zunächst wurde historisch der Teil x0 als skalarer Part bezeichnet. Der Rest, also der Teil mit den imaginären Einheiten, wurde als vektorieller Part bezeichnet. Addiert man zwei Quaternionen x und y und ordnet danach das Produkt wieder in Skalar- und Vektorteil bekommt man:
x = x0 + i·x1 + j·x2 + k·x3
y = y0 + i·y1 + j·y2 + k·y3
x + y = (x0+y0) + i·(x1+y1) + j·(x2+y2) + k·(x3+y3)
Da ist schon recht kompliziert, aber zwei Quaternionen zu multiplizieren ist fast schon qualvoll:
x·y = x0·y0 + i·x0·y1 + j·x0·y2 + k·x0·y3
+ i·x1·y0 + ii·x1·y1 + ij·x1·y2 + ik·x1·y3
+ j·x2·y0 + ji·x2·y1 + jj·x2·y2 + jk·x2·y3
+ k·x3·y0 + ki·x3·y1 + kj·x3·y2 + kk·x3·y3
An dieser Stelle erinnern wir uns an die Produktregeln von oben und fassen alle Produkte von zwei imaginären Einheiten zu einer oder keiner zusammen und stellen danach wieder nach i, j und k um:
x·y = (x0·y0 – x1·y1 – x2·y2 – x3·y3)
+ i·(x0·y1 + x1·y0 + x2·y3 – x3·y2)
+ j·(x0·y2 + x2·y0 + x3·y1 – x1·y3)
+ k·(x0·y3 + x3·y0 + x1·y2 – x2·y1)
Der Zusammenhang mit Vektoren ergibt sich, wenn wir nur Quaternionen x und y betrachten, die keinen Skalarteil haben (x0 = y0 = 0). Dann ergibt sich für die Addition:
x + y = i·(x1+y1) + j·(x2+y2) + k·(x3+y3)
Und für die Multiplikation:
x·y = -(x1·y1 + x2·y2 + x3·y3) + i·(x2·y3 – x3·y2) + j·(x3·y1 – x1·y3) + k·(x1·y2 – x2·y1)
Wenn man jetzt im Geiste frech i, j und k gegen die aus dem Schulunterrucht bekannten Einheitsvektoren ex, ey und ez ersetzt, sieht die Addition von 2 Quaternionen aus, wie die Addition von Vektoren:
x + y = ex·(x1+y1) + ex·(x2+y2) + ex·(x3+y3)
Die Multiplikation beinhaltet das (negative) moderne Skalarprodukt im Skalarteil und das moderne Vektor- oder Kreuzprodukt im vektoriellen Teil des Quaternionenprodukts:
x·y = -(x1·y1 + x2·y2 + x3·y3) + ex·(x2·y3 – x3·y2) + ey·(x3·y1 – x1·y3) + ez·(x1·y2 – x2·y1)
Andere Vektoroperationen, wie z.B. Rotationen lassen sich ähnlich mit Quaternionen durchführen, wodurch klar ist, dass hier endlich ein zufriedenstellendes System vorliegt, Objekte im Raum zu beschreiben und damit zu rechnen. Aufgrund Hamiltons Eifer und seiner Autorität wurden Quaternionen damals weltweit ein Kassenschlager und Hamilton hat den Rest seiner 22 Lebensjahre damit verbracht, sein System zu propagieren und zu erforschen. Aus heutiger Sicht ist das tragisch, weil ein zweifelsfrei genialer Geist so viel Zeit für eine im Nachhinein intellektuelle Sackgasse investiert hat. Was hätte Hamilton wohl noch für die Menschheit leisten können, wenn er nicht so überzeugt von seiner Schöpfung gewesen wäre?
Kommen wir nun zu Hermann Günther Graßmann aus Stettin im preußischen Pommern. Er wurde vier Jahre nach Hamilton geboren und hatte einen Lebenslauf, der unterschiedlicher zu diesem nicht sein könnte. Als Kind fiel er durch “eingeschränkte geistige Spannkraft” auf, später studierte er Theologie und Philologie und entwickelte ein großes Interesse an Mathematik, die er sich autodidaktisch aneignete. Während des Studiums hat er nie eine mathematische Vorlesung gehört. Zeit seines Lebens arbeitete er als Lehrer in Stettin.
Graßmann veröffentlichte “Die lineale Ausdehnungslehre” im Jahr 1844, ein Jahr nach Hamiltons Entdeckung der Quaternionen. Dieses Werk beschreibt die moderne Vektorrechnung und zeugt von Graßmanns tiefem Verständnis für die Mathematik. Sein Vektorsystem ist eingebettet in ein fundamentaleres System, worin n-dimensionale Räume beschrieben und sechzehn verschiedene Produkte zwischen Vektoren, Zahlen und anderen Dingen (inkl. modernem Skalar- und Kreuzprodukt) definiert werden. Damit gilt Graßmann als eigentlicher Begründer der Vektor- und Tensorrechnung und einer der ersten, die sich höherdimensionalen Konzepten widmeten.
Das Problem war allerdings: Seine Arbeit war sehr anspruchsvoll, kein Mensch kannte Graßmann und er verwendete eine selbst erdachte, von üblichen Konventionen abweichende Notation. Niemand wollte das Buch lesen, geschweige denn einen Kommentar dazu schreiben. 15 Jahre nach Erscheinen gab es drei veröffentliche Kommentare. Einer von Graßmann selbst, einer von Möbius und einer von Hamilton im Vorwort eines Lehrbuchs über Quaternionen (immerhin Hamilton hat die Bedeutung von Graßmanns Arbeit verstanden). 20 Jahre nach Erscheinen wurden 600 Kopien des Buchs als Schmierpapier verwendet. Graßmann hat in all der Zeit frustriert um Anerkennung gekämpft und 1862 eine Überarbeitung veröffentlicht, die verständlicher war. 1877, in seinem Todesjahr, schrieb Graßmann darüber: “Diese Arbeit hat noch weniger Aufmerksamkeit erregt als die erste.”
Die Stunde der Quaternionen
Wir schreiben das Jahr 1865, das Jahr in dem Hamilton starb. Quaternionen waren in der Fachwelt als tolle Errungenschaft bekannt und erforscht, aber sie wurden wenig benutzt. Das Graßmannsche System, das der heutigen Vektorrechnung sehr ähnelte, war unbekannt und Graßmann hatte sich mittlerweile einer anderen Disziplin zugewandt: Sprachwissenschaft, wo er ebenso bedeutende Beiträge geleistet hat und auch zu Lebzeiten dafür gewürdigt wurde. Hamiltons “Nachfolger” als Schutzpatron und Erforscher der Quaternionen wurde in dieser Zeit der Schotte Peter Guthrie Tait, ein Kindheits- und Studienfreund von Maxwell. Er hat wichtige Werke geschrieben und großen Wert auf die physikalische Anwendung der Quaternionen gelegt (für Profis: Tait hat intensiv den Nabla-Operator erforscht, der damals auch als Quaternion dargestellt wurde). Es war die Zeit, in der die Elektrodynamik entstand und Maxwell hat seine Gleichungen auch in Quaternionenform angegeben, beeinflusst durch die Arbeiten von Tait. Er hat seine Theorie aber nicht auf Grundlage von Quaternionen entwickelt, weil er kein großer Fan davon war. Seine Meinung zu Quaternionen war, dass die Methoden, räumliche Größen behandeln zu können unschätzbar seien, aber Quaternionen in ihrer Anwendung dabei wenig pragmatisch. Meinungen wie diese sorgten daraufhin, dass sich allmählich das System der modernen Vektoren aus den Quaternionen schälte.
Die Stunde der Vektoren
Was war denn das Problem mit Quaternionen? Es gibt im Wesentlichen zwei große Kritikpunkte. Man kann zwar mit Quaternionen alles machen, was man auch mit modernen Vektoren machen kann, weil Skalar- und Vektorprodukt in der Multiplikation zweier Quaternionen enthalten sind, aber diese Produkte treten in der Rechnung nur gemeinsam auf, wie oben in der Gleichung zu sehen ist. In der physikalischen Bedeutung sind Skalar- und Vektorprodukt aber völlig verschieden und kommen auch in den meisten Fällen nicht gemeinsam zur Anwendung. Auch ergeben sich die beiden Produkte nur, wenn die Skalarteile der beteiligten Quaternionen 0 sind, das komplette Quaternionenprodukt ist für physikalische Anwendung überflüssig. Das Quaternion als vierdimensionale Zahl hat zudem keine anschauliche Bedeutung. Der zweite Kritikpunkt ist das Vorzeichen des Skalarprodukts. In der Formel oben sieht man, dass sich beim Multiplizieren zweier Quaternionen das negative Skalarprodukt ergibt. Das ist unpraktisch, weil sich dadurch alle Gleichungen, wo ein Skalarprodukt berechnet wird, ein Minus einfangen. Als Beispiel sei hier die klassische Definition der kinetischen Energie E eines Körpers mit Masse m genannt:
E = m·v²/2
Das v ist die Geschwindigkeit und eine Größe mit Richtung. Nach damaliger Lesart also ein Quaternion. Die Gleichung der kinetischen Energie lautete also
E = -m·(v²).S/2
Dabei bedeutet (v²).S: Der Skalarteil des Quaternionenprodukts v·v. Das Minus in der Gleichung ist leider notwendig, um das Minus des negativen Skalarprodukts auszugleichen. Das Vorzeichen von einigen Formen von “Energie” ist zwar oft Konvention, aber eine stets negative kinetische Energie ergibt einfach keinen Sinn.
Wie konnte man die Probleme mit Quaternionen lösen? Im Jahr 1881 kamen der amerikanische Physiker Josiah Willard Gibbs und 1883 unabhängig davon der Engländer Oliver Heaviside auf die Idee, die Quaternionen um den Skalarpart zu reduzieren (der ist sowieso in allen Anwendungsfällen 0). Das Quaternionenprodukt spalteten sie in zwei unabhängige Produkte auf, Skalarprodukt und Vektorprodukt. Das Skalarprodukt bekam zudem das umgekehrte Vorzeichen verpasst (v² ≥ 0), sodass die physikalischen Gleichungen wieder intuitiver werden. Gibbs und Heaviside haben ihre Vektormethoden verbreitet und immer mehr Forscher auf ihre Seite gezogen. Die Quaternionen hielten sich noch eine Zeit hartnäckig. Zwischen 1890 und 1910 herrschte ein wahrer Kampf der beiden Systeme, der teils mit harten Worten ausgefochten wurde. Insbesondere Heaviside hatte aber großen Enfluss auf die Verbreitung der Vektoren, weil er als Nachfolger Maxwells in der Entwicklung der Elektrodynamik gilt und dort natürlich sein System verwendete. 1910 hatten sich die Vektoren endgültig durchgesetzt und die Quaternionisten waren überzeugt oder verstorben (eher letzteres).
Interessant ist, dass weder Gibbs noch Heaviside die Arbeit Graßmanns kannten bevor sie die Vektoren erfanden. Obwohl also streng genommen Graßmann als eigentlicher Erfinder des Vektorsystems gilt, ist seine Arbeit von keiner Bedeutung für die Entwicklung des modernen Vektorsystems. Viel wichtiger waren dagegen Hamiltons Quaternionen, die quasi unfreiwillig Schützenhilfe für die Vektoren geleistet haben.
Und heute?
Wenn man mal beide Systeme nebeneinander legt und vergleicht, sieht man das Quaternionen den Vektoren mathematisch eigentlich überlegen sind. Bevor er die Quaternionen entdeckte, suchte Hamilton ein Zahlensystem, das die gleichen Eigenschaften wie die reellen und komplexen Zahlen hat: Assoziativität (A·[B·C] = [A·B]·C) unter Multiplikation, Kommutativität unter Addition und Multiplikation (A·B = B·A), Distribution (A·[B+C] = A·B + A·C), Unzweideutigkeit der Division (A·B = A·C -> B = C), und das sogenannte Gesetz der Moduli (sinngemäß: |A|·|B| = |A·B|). Bis auf die Kommutativität der Multiplikation (zu sehen an i·j = -j·i) besitzen Quaternionen alle diese Eigenschaften.
Bei modernen Vektoren sind zwei verschiedene Multiplikationen definiert. Beim Skalarprodukt ist Assoziativität irrelevant, Division ist nicht eindeutig und das Gesetz der Moduli gilt auch nicht. Das Kreuzprodukt ist zusätzlich noch nicht mal kommutativ. Während das Produkt zweier Quaternionen eigentlich ziemlich intuitiv und gemäß Standardregeln der Algebra definiert ist, sind Kreuz- und Skalarprodukt der Vektoren am Anfang ziemlich verwirrend (zumindest war’s bei mir so). Es sei noch erwähnt, dass es kein Problem ist, Quaternionen mit reellen oder komplexen Zahlen zu addieren oder multiplizieren. Einen Vektor kann man nicht einfach an eine Zahl addieren. Die Vektoren haben sich aber trotzdem durchgesetzt, weil sie einfach anschaulicher sind. Quaternionen sind zwar nette mathematische Spielobjekte, aber das Konzept eines Vektors im Raum versteht wahrscheinlich jedes Kind.
Als kleinen “Bonus” für alle, die bis hierhin durchgehalten haben, gibt es hier die Anleitung, wie man Rotationen mit Quaternionen durchführt: Um einen Vektor (x1, x2, x3) im Raum um den Koordinatenursprung zu drehen, “verpackt” man ihn in ein Quaternion x = (0, x1, x2, x3) und multipliziert dieses von beiden Seiten mit einem Quaternion p:
x’ = p·x·p*
Das Quaternion p = (cos(φ), a1·sin(φ), a2·sin(φ), a3·sin(φ)) beinhaltet den Drehwinkel φ und den Vektor a der Drehachse. p* ist das konjugierte Quaternion von p.
Zum Schluss wollen wir noch klären, warum es trotzdem heute Menschen und technische Zweige gibt, die Quaternionen verwenden. Oben habe ich als Beispiel Computergrafik und Raumfahrt genannt. Das sind Bereiche, wo es auf präzise Berechnungen von Drehungen ankommt und wo unter anderem Geschwindigkeit und Genauigkeit relevant sind. Es werden sehr oft und sehr viele Drehungen berechnet und da ein Computer Zahlen immer runden muss, werden auch kleinste Rechenungenauigkeiten irgendwann ein Problem. Quaternionen sind hierbei numerisch einfacher zu korrigieren (bzw. normieren) als z.B. Drehmatrizen und werden daher gerne bei Computerberechnungen benutzt. Ob Vektoren anschaulicher sind, ist einem Computer völlig egal.
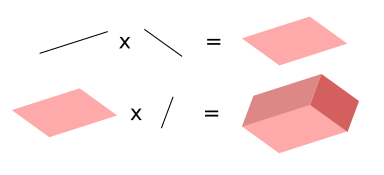
Kommentare (26)