Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Umformen – quick and dirty
von Benjamin Remmers
Ich bin Maschinenbaumechanikergeselle und -ingenieur, wissenschaftlicher Mitarbeiter, Familienvater, podcastabhängig.
In einem Laborpraktikum im ersten Semester des Maschinenbaustudiums führe ich mit Studierenden einen Laborversuch an einer Reibradspindelpresse durch. Da die Studierenden zu diesem Zeitpunkt noch keine einschlägigen Vorlesungen gehört haben, muss ich auf die Schnelle die benötigte Formel herleiten und dabei die Grundlagen anreißen. Die wissenschaftliche Tiefe bleibt dabei natürlich ein wenig auf der Strecke, daher: quick and dirty und mit viel Augenzwinkern.
Im diesem Laborversuch soll aus der Formänderung einer Probe das Arbeitsvermögen einer Reibradspindelpresse bestimmt werden. Dieses Vorgehen kann man z. B. bei einer Maschinenprüfung im Rahmen einer regelmäßigen Wartung benutzen.
Eine Reibradspindelpresse ist eine sogenannte arbeitsgebundene Maschine. Das bedeutet in diesem Fall, dass das Arbeitsvermögen in Form von Bewegungsenergie vorliegt. Bei einem Umformprozess wird nun der Hauptteil dieser kinetischen Energie in die Umformung gesteckt und damit letztendlich in Wärme umgewandelt. Warum? Unsere Probe, ein Zylinder aus einer Aluminiumlegierung (AlMg3 H22), ist aus Kristalliten aufgebaut. Wenn jetzt auf die Kristallite eine Kraft wirkt, können die Atome im Gitter entlang der Gleitebenen gegeneinander verschoben werden, dabei entsteht Reibung und dabei entsteht Wärme. Auch durch die Messung der Wärmemengen-Änderung könnte man die Umformarbeit bestimmen. Doch ich schweife ab…
Je mehr Energie zur Verfügung steht, desto stärker wird sich die Probe umformen. Doch was heißt eigentlich “umformen”? Für uns Produktionstechniker heißt “umformen”, dass sich bei einem Werkstück die äußere Form ändert, ohne dass sich gewollt andere Eigenschaften verändern (auch wenn das praktisch natürlich anders ist). Im Speziellen spricht man von Volumenkonstanz (auch wenn Massenkonstanz eigentlich richtiger wäre). Drücke ich nun bei unserer zylindrischen Probe von den Stirnseiten aus auf die Probe, wird sie flacher und damit auch breiter. Wenn ich nun über die Umformung die Arbeit bestimmen möchte, brauche ich zunächst einmal eine Größe, mit der ich die Umformung darstellen kann.
Das erste, was den meisten Leuten einfällt, ist die Höhendifferenz, also
Der geneigte Leser fragt sich nun: Benötige ich für die Verkürzung einer Probe von 20mm auf 10mm die gleiche Energie wie für die Umformung einer 1000mm-Stange auf 990mm?
Vom Bauchgefühl her scheint diese Lösung unbefriedigend. Was soll man also tun? Man versucht es mit der Punktrechnung. Man könnte ja ein Verhältnis bilden und die Ausgangslänge miteinbeziehen:
Diese Formel definiert die Dehnung. Sie findet sich prominent in einem der Diagramme, ohne die man nicht Maschinenbau studieren kann, dem Spannungs-Dehnungs-Diagramm:
An diesem Diagramm kommt im Maschinenbaustudium niemand vorbei. Urheber: B. Remmers, CC0
Dieses Diagramm ist werkstoffspezifisch und stammt aus dem Zugversuch. In diesem Versuch aus der Werkstoffkunde wird eine Probe mit bekanntem Querschnitt an ihren Enden in eine Zug-Prüfmaschine eingespannt und in die Länge gezogen. Dabei werden die Längenänderung und die wirkende Zugkraft gemessen. Die in der Probe herrschende Spannung wird berechnet, indem man die momentane Kraft durch die Querschnittsfläche teilt.
Beginnt man zu ziehen, befindet man sich zunächst im linken Bereich auf der Hookeschen Geraden. Hier ist die Formänderung elastisch, d.h. noch ist keine bleibende Umformung passiert. Wer schon einmal mit einer Büroklammer gespielt hat, kennt das als Rückfedern. Zieht man weiter, passiert häufig etwas Seltsames: Die Gerade knickt ab und beginnt zu flattern. Dies ist die ausgeprägte Streckgrenze. Danach beginnt nun die plastische Formänderung, es gibt also kein Zurück mehr in den Ausgangszustand. Dass die benötigte Kraft jetzt noch weiter ansteigt, liegt an der Kaltverfestigung. Diesen Effekt kennt man ebenfalls von der Büroklammer: Versucht man den Knick von eben wieder wegzubekommen, stellt man fest, dass der Draht sich lieber neben der eben gebogenen Stelle biegen möchte. Das liegt daran, dass der Werkstoff fester wird, je weiter ich ihn umforme (Versetzungen, die sich behindern und so).
Aber irgendwann werden die Spannungen in der Zugprobe wieder weniger. Wer lügt denn nun: Ich mit der Kaltverfestigung oder das Diagramm?
Das Diagramm lügt. Ab dem Spannungsmaximum beginnt sich die Probe einzuschnüren (wir erinnern uns an die Volumenkonstanz). Da für die Bestimmung der Spannung aber munter weiterhin durch den Ausgangsquerschnitt der Probe geteilt wird, entspricht die dargestellte (Ingenieurs-)Spannung gar nicht mehr der wahren Spannung.
Für unseren Versuch scheint das Spannungs-Dehnungs-Diagramm also aus zwei Gründen nicht geeignet zu sein: Erstens interessiert uns Umformer die elastische Formänderung nicht und zweitens stimmt die Kurve im relevanten Bereich nicht.
Und auch die Dehnung als Kennwert für die Umformung ist anzuzweifeln. Stellen wir uns eine Probe von 100mm Länge vor, die wir um 10mm zusammendrücken, so bekommen wir eine Dehnung von 10%. Machen wir die Umformung durch Ziehen wieder Rückgängig, erhalten wir eine Dehnung von 11%. Und eine Kenngröße, die für Hin- und Rückweg unterschiedliche Beträge annimmt, können wir hier nicht gebrauchen.
Was tut der geneigte Wissenschaftler, wenn die Punktrechnung versagt? Er logarithmiert.
Dies ist der Umformgrad. Für ihn bekommen wir bei dem Beispiel für Hin- und Rückweg denselben Betrag nur mit unterschiedlichen Vorzeichen (die verraten uns dann, ob gerade eine Dehnung oder eine Stauchung vorliegt). Passt.
Das für uns interessante Diagramm ist die Fließkurve. Sie ist die bildliche Darstellung der Kaltverfestigung. Auf der x-Achse ist der Umformgrad, auf der y-Achse die Formänderungsfestigkeit (die wahre Spannung) aufgetragen. Je weiter man umformt, desto fester wird der Werkstoff.
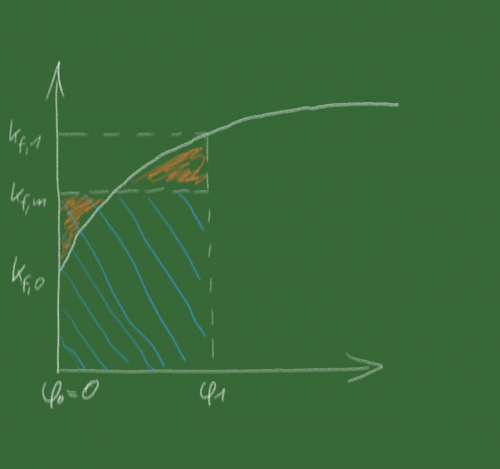
Eine Fließkurve mit mittlerer Formänderungsfestigkeit, Urheber: B. Remmers, CC0
Das, was wir nun zur Berechnung der Umformarbeit benötigen, findet sich wie so oft in der Fläche unter der Kurve. Mathematisch gesprochen ist es das Integral der Fließkurvenfunktion in den Grenzen vom Zustand vor der Umformung (0) bis zum Zustand nach der Umformung (1). Aus dem Zugversuch fällt aber nur das Diagramm heraus. Und abgesehen davon ist das Integrieren sowas von oldschool. Und wir Fertigungstechniker sind normalerweise eher pragmatisch.
Man könnte jetzt das Diagramm in ein doppelt-logarithmisches Koordinatensystem eintragen und von der dann entstandenen Geraden einen Stützpunkt und die Steigung bestimmen…
Oder wir erlauben uns eine kleine Annäherung: Schaut man sich die Kurve an, stellt man fest, dass man die unregelmäßige Fläche auch durch ein Rechteck ersetzen kann, wenn man die mittlere Fließspannung verwendet und dann das Flächenstück über der oberen Seite benutzt, um die Lücke unter der Seite zu füllen. Eine Rechteckfläche lässt sich sehr leicht berechnen. HAbe ich schon erwähnt, dass Fertigungstechniker eher faul pragmatisch sind?
Jetzt brauchen wir für die Formel der Umformarbeit nur noch die Erkenntnis, dass wir mehr Arbeit benötigen, je mehr Material wir umformen. Da es ja die Grundregel der Volumenkonstanz gibt, bietet sich dafür das Zylindervolumen an.
Die Formel für die theoretische Umformarbeit ergibt sich nun zu:
Die Rechteckfläche aus der Fließkurve multipliziert mit dem Volumen der Probe.
Ich hoffe, ich konnte Euch einen kleinen Einblick in die Theorie der Umformtechnik bieten. Denkt daran, wenn Ihr das nächste Mal eine Münze, eine Getränkedose oder eine Autotür in der Hand habt, denn alle diese Teile sind mittels Umformverfahren hergestellt und vorher so oder so ähnlich (z. B. FEM basiert auf diesen Diagrammen und Formeln) berechnet worden.
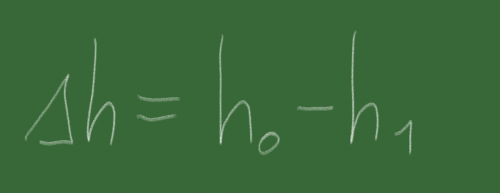
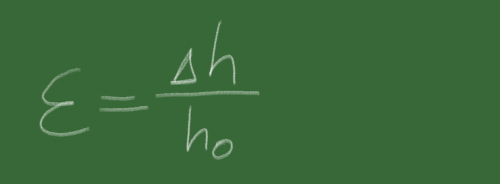
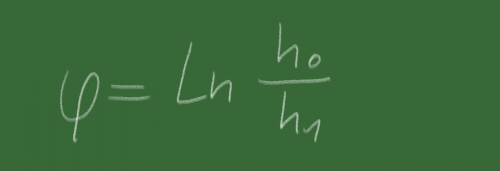
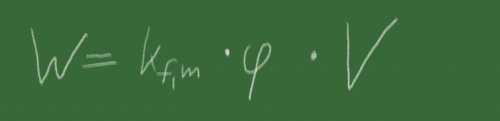
Kommentare (26)