Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
————————————————————————————————————–
Wie Computer intelligent(er) wurden
von Jörg D.
Ich habe theoretische Physik im wunderschönen Jena studiert. Heute schreibe ich aber über meine zweite große Leidenschaft: Neuronale Netzwerke und künstliche Intelligenz
Neuronale Netzwerke sind in aller Munde. Sie besiegen Weltmeister im Go, sie malen Bilder, sie hören uns zu und übersetzen unsere Sprache. Das sind alles Tätigkeiten, die recht komplex erscheinen, sind neuronale Netzwerke (NNs) also super-komplizierte Gebilde, die nur die intelligentesten 0,1 % der Weltbevölkerung jemals verstehen könnten? In diesem Beitrag möchte ich zeigen, dass dies nicht ansatzweise stimmt, dass jeder zumindest die Grundlagen neuronaler Netze verstehen kann.
Ich stand vor einiger Zeit vor der Aufgabe, eine Software zu entwickeln, die entscheiden kann, ob in einem Bild ein Mensch, ein Auto oder ein Hund zu sehen ist. Diese Aufgabenstellung ist viel älter als der aktuelle Hype um künstliche Intelligenz und man findet viele Arbeiten zu diesem Thema. Ich habe auch zunächst mit „klassischen“ Ansätzen wie Haarfiltern (hat nichts mit Haaren zu tun), HOGs (hat nichts mit Wildschweinen zu tun) und Supportvektormaschinen (hat zwar mit Supportvektoren zu tun, aber das Wort Maschine ist hier sehr frei benutzt) experimentiert und deren Ergebnisse waren zwar durchaus gut, aber längst nicht gut genug für mich. Ich hatte zwar zu dieser Zeit schon von NNs gehört, aber ich dachte, dieses Thema wäre doch viel zu groß für mich und ich müsste nochmal 5 Jahre studieren, um die verstehen zu können. Ich hätte nicht falscher liegen können!
Als die Frustration zu groß wurde, aber auch die Neugier stieg, habe ich doch mal einen Wikipedia-Artikel gelesen, dann noch ein paar weitere Artikel und schließlich innerhalb einer Woche ein sehr schönes Online-Buch verschlungen und plötzlich hatte ich ein recht gutes Verständnis von NNs. Hier möchte ich meine Erkenntnisse teilen.
Vorweg: Ich werde über einen recht einfachen Typ von NNs schreiben, die lediglich ein Bild entgegennehmen und dann entscheiden, ob es zu einer vorher festgelegten Kategorie gehört. Netzwerke, die die in der Einleitung genannten Aufgaben meistern, sind nochmal eine Stufe umfangreicher, aber mit diesem Artikel hat man, hoffe ich, zumindest genug Grundlagen, um sich auch darin einzulesen.
Der Input
Wir geben dem Computer also ein Bild. Dieses Bild ist für den Computer aber nur eine Menge aus Zahlen, darüberhinaus sieht er nicht so, wie wir Menschen dies können. Jeder Pixel des Bildes besteht aus Zahlen, und zwar 3: Eine für den Rot-Anteil, eine für den Blau-Anteil und eine für den Grün-Anteil. Aus diesen Informationen kann der Bildschirm dann später berechnen, welches Licht er abstrahlen muss.
Der Einfachheit halber möchte ich mich hier auf Graustufenbilder beschränken, die an jedem Pixel nur eine Zahl haben, die die Helligkeit angibt. Meistens sind die Zahlen dann auf den Bereich von 0 bis 255 normiert, sodass 0 schwarz und 255 weiß bedeutet und die Zahlen dazwischen die entsprechenden Graustufen sind. Diese Ansammlung aus Zahlen, die ja im Falle zweidimensionaler Bilder in Zeilen und Spalten angeordnet sind, kann man dabei gut und gerne als Matrix interpretieren.
Der erste Filter
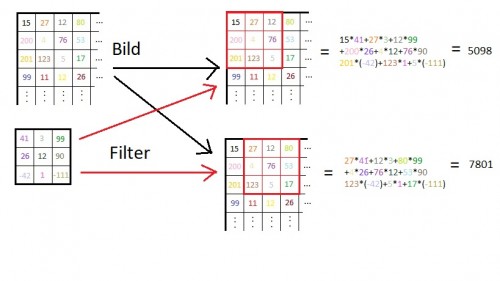
Diese Matrix wird nun analysiert. Dazu werden Filter über die einzelnen Einträge gelegt. Ein Filter ist nur eine weitere Matrix, zum Beispiel mit 3×3 Einträgen. Legt man diese über unsere Bild-Matrix wie in Abb. 1 angedeutet, kann man die Einträge, die „aufeinanderliegen“ miteinander multiplizieren und zum Schluss alles addieren.
Das klingt alles sehr theoretisch und mathematisch-langweilig. (Das ist natürlich ein sehr schlechter Witz. Mathe ist niemals langweilig!) Interessant wird es aber, wenn wir uns den Filter genauer ansehen: Es gibt positive und negative Einträge. Wann erzeugt der Filter das größte Ergebnis? Dann, wenn die Einträge der Bild-Matrix, die dort liegen, wo der Filter positiv ist, möglichst groß sind (255 ist ja das Maximum) und die Einträge der Bild-Matrix, die bei negativen Filter-Einträgen liegen, möglichst klein sind (0 ist das Minimum).
Abb.1 Allgemeiner Ablauf der Filterung (Ausgeburt meiner Paint-Künste)
Nun kann man den Filter auch wieder als Bild interpretieren (die negativen Einträge setzen wir dann zu 0). Das heißt, der Filter erzeugt ein großes Ergebnis, wenn die Bild-Matrix an dieser Stelle ihm möglichst ähnlich sieht. Sieht die Bild-Matrix ganz anders aus, wird das Ergebnis sehr klein, vielleicht 0 oder sogar negativ.
Abb. 2 Verschiedene Bilder mit dem gleichen Filter (Noch ein Produkt meines Paint)
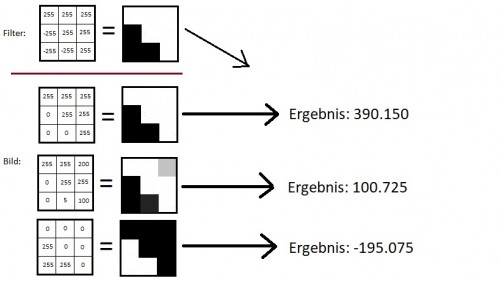
In Abbildung 2 habe ich mal ein paar Beispiele gezeigt: Der Filter sieht aus wie eine schräge Kante. Wenn das Bild auch wie eine schräge Kante aussieht, bekommen wir ein sehr großes Ergebnis. (in der Praxis teilt man übrigens noch durch alle möglichen Werte und arbeitet mit kleineren Zahlen) In der zweiten Zeile im Bild (oder der dritten, aber da Programmierer bei 0 anfangen, zu zählen, ist „zwei“ auch in Ordnung) sieht das Bild ein wenig nach schräger Kante aus, aber sie ist nicht ganz perfekt. Wir bekommen aber immer noch ein recht hohes Ergebnis. Das ist sinnvoll, da die reale Welt ziemlich schmutzig ist und Schatten, schlechte Kameras oder Hindernisse eine perfekte Kante schnell zunichte machen können.
In der dritten Zeile haben wir dann das genaue Gegenteil unseres Filters (eigentlich ist es ja auch eine schräge Kante, aber in die umgekehrte Richtung), entsprechend wird das Ergebnis sehr negativ.
Zwei Details sind dabei noch zu beachten: Zum einen wird auf das Ergebnis des Filters immer noch ein Wert addiert (oder subtrahiert, falls der Wert negativ ist). Auf diese Art kann man bestimmte Filter, z.B. gerade Kanten, „wichtiger“ machen und andere Arten von Kanten quasi unterdrücken. (Beispiel: Wir wollen mit unserem Netzwerk Bälle finden. Es ist zwar schon, wenn wir dabei gerade Kanten finden, aber eigentlich haben Bälle nur runde Kanten, also bekommen die geraden Kanten eine kleinere Wichtigkeit)
Das andere Detail ist, dass negative Ergebnisse tatsächlich nicht einfach behalten werden, sondern zu 0 gesetzt werden. Das bringt die nötige mathematische Nichtlinearität und damit Kompliziertheit, um so komplizierte Aufgaben wie Objekterkennung wirklich meistern zu können. (das war jetzt ein wenig schwammig, aber tatsächlich steckt die ganze Theorie hinter NNs noch ziemlich in den Kinderschuhen. Viele Sachen werden gemacht, weil sie funktionieren)
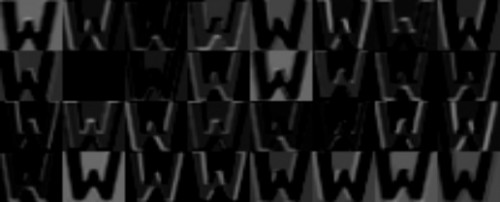
Nun können wir unseren Filter über jede Stelle unseres Bildes fahren lassen und jedes Mal das Ergebnis notieren. So wie der Filter dann über die Zeilen und Spalten des Bildes fährt, können wir die Ergebnisse wieder in Zeilen und Spalten anordnen. Wir erhalten also eine neues Bild, das eine hohe Zahl hat (und damit besonders weiß erscheint), wo das alte Bild dem Filter ähnlich war. Wenn der Filter also z.B. aussah wie eine schräge Kante, dann ist das Ergebnis eine Art Karte, die zeigt, wo im Bild schräge Kanten waren. In Abbildung 3 und 4 habe ich dies mal für mehrere Filter aus einem von mir selbst erstellten Netzwerk gezeigt. (Ich habe Buchstaben genommen, weil man dort Kanten besonders schön sieht und man diese gut verkleinern kann, um alles in ein Bild zu bekommen, und trotzdem noch etwas erkennt) Man sieht stellenweise sehr schön, wie das Ergebnis besonders „hell“ ist, wo eine Kante bestimmter Richtung zu sehen ist. Stellenweise ist das ganze Bild mehr oder weniger hell, wird an Kanten aber erst richtig weiß. Im zweiten Bild von links in der zweiten Zeile sieht man jeweils – nichts. Da war wohl nichts da, was den Filter angesprochen hätte.
Ein Bild von einer 8, nachdem 32 Filter darübergelaufen sind (Produkt meines höchst-eigenen Python-Skipts und eines selbstgemachten NNs)
Noch ein Bild von einem W mit den gleichen Filtern (ebenfalls 100% von mir)
Nun verwendet man für ein NN nicht nur einen solchen Filter, sondern viele. Wie viele genau, das ist nicht festgelegt. Im Zweifelsfall findet man durch experimentieren heraus, mit welcher Anzahl man die besten Ergebnisse erhält. Im oben erwähnten Beispiel habe ich 32 Filter benutzt, hatte nach dem ersten Schritt also 32 „Kanten-Bilder“, wie die eine oder andere vielleicht schon nachgezählt hat. (die Filter müssten nicht wie Kanten aussehen, sondern können eigentlich beliebige Formen haben, aber der Einfachheit halber spreche ich auch im Folgenden von Kanten)
Ein Wort zum Vokabular noch: Die Operation, eine Filter-Matrix auf die Bild-Matrix anzuwenden, wird von Mathematikern als „Faltung“ bezeichnet, auf Englisch: Convolution. Daher hat dieser Typ NN seinen Namen: Convolutional Neural Network, oder kurz CNN.
Die weiteren Filter
Wir haben nun also 32 Kanten-Bilder. Das ist schön, aber noch nutzlos. Wir können auf diese Bilder nun aber wieder neue Filter anwenden. Im ersten Schritt war ein Filter ja eine 3×3-Matrix, nun besteht ein Filter aber aus 32 3×3-Matrizen, jede wird auf ein Kanten-Bild angewendet und alle Ergebnisse werden addiert. Im ersten Schritt haben wir helle und dunkle Pixel zu Kanten zusammengebaut. Nun können wir Kanten zusammenbauen zu – naja, zum Beispiel zu geometrischen Formen: Zum Beispiel können 2 senkrechte und 2 waagerechte Kanten ein Viereck bilden. Wir können also einen Filter bauen, der diesmal zeigen wird, wo im originalen Bild Vierecke waren. Ein anderer Filter könnte Kreise oder Dreiecke zeigen.
So können wir wieder 32 neue Bilder erzeugen, diesmal eben für geometrische Formen. (wir können aber auch mehr Filter benutzen und noch mehr Bilder machen, wie gesagt, die Zahlen sind hier nicht gesetzlich festgelegt) Nun können wir auf diese Bilder im nächsten Schritt wieder Filter anwenden, die die geometrischen Formen zu komplizierteren Formen zusammenbauen und so weiter und so weiter. Nach genug Schritten können wir auf diese Art Filter haben, die Gesichter, Autoreifen oder Hundenasen erkennen.
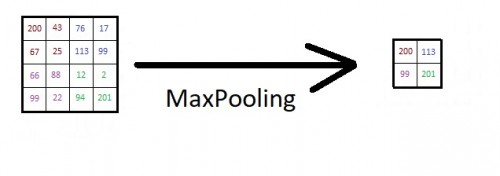
Bildverkleinerung für Zwischendurch
Unser Netzwerk ist also nur eine Reihe von aufeinanderfolgenden Filtern. Richtig? Nicht ganz. Ab und zu schaltet man noch ein sogenanntes MaxPooling dazwischen. Das Prinzip ist ähnlich zu den Filtern: Man nimmt sich z.B. einen 2×2-Bereich eines Bildes heraus und schaut, welche Zahl in diesem Bereich am größten ist. Diese Zahl behält man, alle anderen schmeißt man weg. Damit schrumpft das Bild auf ein Viertel zusammen. Das hat zwei Vorteile: Zum einen werden die Bilder, die man filtern muss, deutlich kleiner. Das spart Rechenzeit. Das ist gut, denn Rechenzeit ist teuer! Zum anderen wird man dadurch ein wenig unabhängiger von der exakten Lage der Kanten/Formen/was-auch-immer im Bild. Ein Mensch bleibt ein Mensch, auch wenn er einen Zentimeter weiter links/rechts/oben/unten ist.
Abb. 5 Ablauf des MaxPoolings (wieder von mir und Paint)
Das Ende: Jeder mit jedem
Nachdem wir nun ein paar mal Filter angewendet haben und ab und zu unser Bild verkleinert haben, haben wir nun eine Ladung kleiner, gefilterter Bilder. Diese müssen nun final ausgewertet werden, um zu entscheiden, ob wir die Arme, Augen und Köpfe darin zu Menschen zusammenbauen können oder ob da doch eher ein Hund zu sehen ist oder nichts von alledem.
Dafür verwenden wir nun keine kleinen 3×3-Filter mehr, sondern die finalen Filter haben die Größe der kompletten Bilder. Es wird alles, also ALLES, zusammengewürfelt, multipliziert und ein Ergebnis notiert. Man hat wieder mehrere solcher Filter, deren Ergebnisse notiert man nun nicht mehr als Matrix, sondern als Vektor. Diesen Vektor könnte man nun wieder filtern und so weiter. Am Ende steht dann aber ein Vektor, der so viele Einträge hat, wie wir Kategorien haben. Wenn wir also Menschen, Hunde und Autos erkennen wollen, hat unser letzter Vektor 3 Einträge. Diese kann man mit ein wenig Mathe-Magie so umrechnen, dass sie Wahrscheinlichkeiten angeben, also z.B. „Mit 90-prozentiger Wahrscheinlichkeit ist das im Bild ein Mensch, mit 9-prozentiger Wahrscheinlichkeit ein Hund und mit 1-prozentiger Wahrscheinlichkeit ein Auto“. Das ist das finale Ergebnis, damit sind wir fertig. Hurra! Unser Computer ist so schlau wie ein Kleinkind. Ein Kleinkind, das nur drei Dinge kennt.
Noch ein Wort zum Vokabular: Weil hier alles mit allem verbunden ist, nennte man diesen Filterabschnitt “Fully Connected Layer”, andernorts sagt man aber auch “Dense Layer”.
Zurück zum Anfang: Das Training
Wer jetzt begeistert seinen bevorzugten Editor öffnet und selbst anfangen will, so ein NN zu programmieren (und so schwer ist das ja eigentlich alles gar nicht), wird vermutlich recht schnell auf eine sehr gewichtige Frage stoßen: Wie genau soll ich die Filter eigentlich aussehen lassen? Welche Zahlen kommen dort rein?
Früher, in der grauen Ära vor neuronalen Netzwerken, haben die Wissenschaftler wirklich noch versucht, alle Parameter selbst zu setzen. Das geniale an NN ist aber, dass das gar nicht notwendig ist, sie finden die richtigen Werte von selbst! Dazu braucht man zunächst eine große Menge von Bildern, die man vorher „per Hand“ sortiert hat, das heißt, man weiß, wo Menschen, Autos etc. sind. Dann nimmt man ein NN her, deren Filter man zunächst mit zufälligen Zahlen gefüllt hat. Unter diesen Umständen kommen vermutlich komplett unsinnige Ergebnisse raus, z.B. bei einem Bild von einem Menschen antwortet der Computer „Mit 24-prozentiger Wahrscheinlichkeit ist das im Bild ein Mensch, mit 62-prozentiger Wahrscheinlichkeit ein Hund und mit 14-prozentiger Wahrscheinlichkeit ein Auto“.
Tatsächlich sollte ein perfektes Netzwerk hier aber 100% Mensch sagen (und 0% für Hund und Auto). Man kann nun eine mathematische Formel angeben, die beschreibt, wie groß der Fehler ist und man versucht, diesen Fehler zu minimieren. Diese Formel bzw. der Fehler hängt nun aber von allen Einträgen der Filter ab, d.h. man kann tun, was Wissenschaftler immer tun, wenn sie eine Formel haben: Sie leiten sie ab. Indem wir wissen, wie sich der Fehler mit den Einträgen der Filter ändert, wissen wir, wie wir die Filter ändern müssen, um dem richtigen Ergebnis näher zu kommen. (Praxistipp: Wenn ihr eine Fehler-Funktion selbst geschrieben habt und diese von Anfang an nur 0 ausgibt und auch dabei bleibt, schaut euch euren Code nochmal an…) Ich schreibe bewusst „näher kommen“, denn man kann das immer nur Schritt für Schritt machen und um ein wirklich gutes Netzwerk zu bekommen, das wirklich lernt, was einen Menschen ausmacht und was einen Hund, sollte man ihm möglichst viele Bilder (hunderte, besser tausende) zeigen. Wer mit NNs arbeitet, verbringt daher einen guten Teil seiner Zeit damit, einfach nur stupide Bilder zu sammeln und mit Labeln zu versehen. (man wünscht sich, man hätte ein Computerprogramm, das Menschen erkennt, um die Daten zu sortieren, damit man dann ein Programm schreiben kann, das Menschen erkennt…)
Zum Schluss kann man als Mensch zwar nur noch schwer nachvollziehen, wie der Computer da eigentlich auf die Zahlen gekommen ist, die er nun verwendet, aber sie funktionieren und sie funktionieren gut!
Nachwort
Ich habe verdammt viele Details ausgelassen. Wie aber eingangs erwähnt, wollte ich nur ein grobes Verständnis geben, wer einmal verstanden hat, wie die Filter und MaxPooling funktionieren, hat eigentlich schon die halbe Miete. In der Praxis setzt man das dann nur noch auf verschiedene Weise zusammen, um die Funktion zu bekommen, die man möchte.
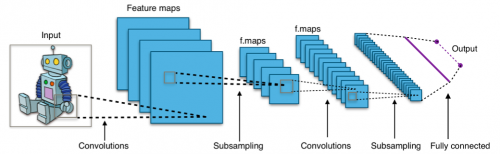
Abb. 6: Ein CNN visualisiert. Die einzelnen Filter-Schritte stellt man sich als Schichten vor. Mit “Subsampling” ist im Bild das MaxPooling gemeint. (wer es bis hier durchgehalten hat, bekommt zur Belohnung noch ein professionelles Bild: Aphex34, Typical cnn, CC BY-SA 4.0 )
Die Beschäftigung mit NNs ist übrigens nicht nur sehr cool, man lernt dabei auch vieles über sich selbst: Das Prinzip mit den verschiedenen Filterungen ist vom Gehirn inspiriert. Andere Netzwerktypen versuchen, Spiele zu erlernen wie ein echter Mensch dies tun würde, wieder andere organisieren Daten nach dem Vorbild von Strukturen im Gehirn. Wer sich eher für Mathematik interessiert, kann versuchen, die Theorie hinter NNs besser zu verstehen. Obwohl man nämlich, wie erwähnt, in der Praxis durch gutes altes Ausprobieren schon überwältigende Ergebnisse erzielt hat, ist die ganze Theorie dahinter noch in den Kinderschuhen. Aber auch das Ausprobieren, mit Variablen spielen und dem optimalen Ergebnis Schritt für Schritt näher kommen erinnert mich ehrlich gesagt sehr an mein Physikstudium.
Wer enttäuscht ist, dass ich nur auf die Analyse von Bilder eingegangen bin, nicht aber auf das Erkennen von Sprache oder das Go-Spielen: Sprache lässt sich z.B. als Sonagramm auch in ein Bild umwandeln und das Go-Brett ist im ersten Schritt auch erst mal ein Bild, das man auswerten muss. Also ja, es hängt alles zusammen.
Ich hoffe, ich konnte dem ein oder anderen etwas neues beibringen und freue mich auf rege Diskussionen und interessante Fragen in den Kommentaren.
Kommentare (24)