 Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
————————————————————————————————————–
Aus wie vielen Quarks besteht ein Proton?
von Reggid
„Ein Proton besteht aus zwei Up und einem Down Quark.“ Das ist eine jener Tatsachen, an die sich manche vielleicht aus dem Physikunterricht erinnern können, oder allgemein an Teilchenphysik interessierte Menschen schon oft gehört haben. Diese Darstellung hat ihre Berechtigung – und ist dennoch für alles was in modernen Collider Experimenten wie z.B. dem LHC am CERN geschieht völlig unbrauchbar. Denn auch hier gilt ein eisernes Gesetz der Physik: in Wirklichkeit ist ja doch alles immer ein bisschen komplizierter. Denn man findet auch Strange Quarks im Proton, ja sogar Antiquarks kann man darin nachweisen.
Der Blick von außen: Warum ein Proton aus drei Quarks besteht
Wie kommt man also zu der Auffassung dass ein Proton (und auch Neutron) aus exakt drei Quarks besteht? Man kann dies aus verschiedenen Beobachtungen ableiten. Ich werde hier nicht allzu sehr ins Detail gehen wie man das macht (und wie es historisch geschehen ist), ich denke es gibt sehr viele sehr gute Artikel dazu die das beschreiben. Mir geht es mehr darum im weiteren Verlauf zu zeigen warum dieses einfache Modell eben gerade nicht ausreichend ist.
Quarks sind nach heutigem Kenntnisstand fundamentale Elementarteilchen wie es z.B. auch Elektronen sind. Sie tragen elektrische Ladung, eine sog. Farbladung (die Ladung der starken Wechselwirkung. Das Wort „Farbe“ darf man hier auf keinen Fall wörtlich nehmen) und sie haben einen gewissen Eigendrehimpuls, ein bisschen so als würden sie um die eigene Achse rotieren. Aus verschiedenen Eigenschaften von Protonen und Neutronen (und weiteren Teilchen wie z.B. den schwereren Delta-Baryonen) kann man folgern dass alle diese aus kleineren Teilchen, eben diesen Quarks und drei an der Zahl, zusammengesetzt sind. Ich werde hier nur ein paar Beispiele anführen an denen man sieht dass diese Eigenschaften eines Protons in der Tat exakt damit übereinstimmen dass es aus drei dieser Quarks besteht.
So weiß man z.B. dass die elektrische Ladung eines Protons genau einer positiven Elementarladung entspricht, während ein Neutron keine elektrische Ladung trägt. Dies passt genau damit zusammen dass ein Proton aus zwei Quarks mit elektrischer Ladung +2/3 (genannt Up Quarks) und einem mit elektrischer Ladung -1/3 (genannt Down Quark) besteht und ein Neutron aus zwei Down Quarks und einem Up Quark. Des Weiteren haben sowohl Proton als auch Neutron einen Eigendrehimpuls der genau einer der möglichen Kombinationen der Drehimpulsen von drei Quarks entspricht. Außerdem tragen sowohl Proton als auch Neutron keine Farbladung (sind also nach außen hin unter der starken Wechselwirkung neutral), was wiederum damit zusammen passt dass sie aus genau drei Quarks bestehen. Denn so wie ein positiv und ein negativ elektrisch geladenes Teilchen in Summe ein neutrales Teilchen bilden können, so können drei Teilchen welche eine Farbladung tragen in Summe eine „farbneutrales“ Teilchen wie z.B. ein Proton bilden.
Somit weiß man also dass ein Proton aus drei Quarks besteht, zwei Up und ein Down Quark um genau zu sein. Bei einem Neutron wären es ein Up und zwei Down Quarks. Zusammengehalten werden die Quarks durch die starke Wechselwirkung, das bedeutet durch Wechselwirkung mit dem Gluonfeld, und somit kommt man dann zu der Vorstellung eines Protons wie sie nachfolgend dargestellt ist: Drei Quarks, die irgendwie durch Gluonen zusammengehalten werden. Gut beschrieben ist das z.B. hier.
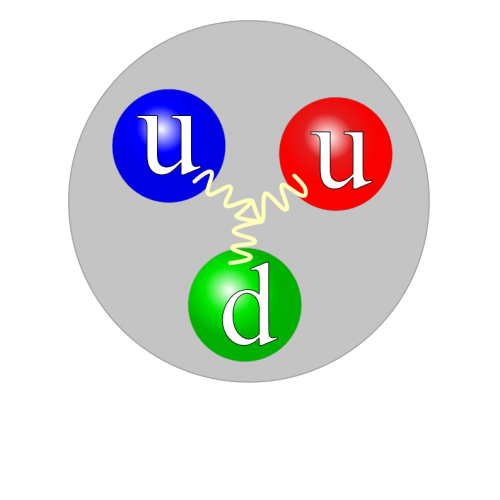
So sieht ein Proton aus – sagt Wikipedia. (Jacek rybak, Proton quark structure, CC BY-SA 4.0)
Von sog. Strange Quarks (einer weiteren Sorte von Quarks neben den Up und Down Quarks) oder sogar Antiquarks (also den Antiteilchen zu den normalen Quarks) sehen wir an diesen Punkt noch gar nichts. Aber ist das wirklich schon alles? Bis jetzt haben wir das Proton eigentlich nur von außen betrachtet, also Eigenschaften die es nach außen hin hat wie seinen Drehimpuls, seine Farbladung, seine elektrische Ladung, usw. … . Aber wir können, vorausgesetzt man hat einen Teilchenbeschleuniger mit genügend großer Leistung zur Hand, auch in das Proton hinein blicken und in hochenergetischen Kollisionen seine innere Struktur direkt studieren.
Der Blick ins Innere: Warum ein Proton nicht aus drei Quarks besteht
Gehen wir also jetzt ein bisschen mehr in die Tiefe. Wobei „ein bisschen“ vielleicht etwas untertrieben ist, denn recht viel tiefer geht es wirklich nicht mehr. Weder im übertragenen Sinne (wir sind bei dem Folgenden bereits sehr nahe dran am state of the art der modernen Teilchenphysik) als auch wörtlich (noch tiefer ins Proton können wir mit unserer derzeitigen Technik nicht blicken). Es wird hier die eine oder andere Formel auftauchen, aber auch diejenigen die mit solchen mathematischen Ausdrücken nicht so vertraut sind brauchen sich keine Sorgen zu machen. Ich werde versuchen den Inhalt jeder einzelnen dieser Formeln in Worten zu erklären.
Wie stellt sich ein Proton also aus der Sicht einer Teilchenphysikerin dar, der z.B. am LHC arbeitet und dort Protonen mit extrem hoher Energie kollidiert? Wie wir gleich sehen werden doch etwas anders als es das naive Bild von oben beschreibt.
Was also macht der LHC, der größte bisher gebaute Teilchenbeschleuniger? In ihm werden Protonen (und manchmal auch Blei-Ionen, aber die lassen wir mal beiseite) fast auf Lichtgeschwindigkeit beschleunigt und zur Kollision gebracht. In diesen hochenergetischen Kollision entsteht eine Vielzahl von neuen Elementarteilchen, welche dann teilweise wieder in weitere Teilchen zerfallen, bis man in den riesigen Detektoren die um die Kollisionspunkte herum gebaut sind alle diese Teilchen und ihre Energie und Impuls messen kann. Aus der genauen Verteilung dieser Teilchen versucht man dann Rückschlüsse über die Wechselwirkungen die an der Kollision und den Zerfällen beteiligt waren zu ziehen. Dort kollidieren also Protonen mit hoher Energie. Wir wissen aber bereits dass Protonen keine fundamentalen Elementarteilchen sind, sondern aus Quarks und Gluonen bestehen. Was dort also eigentlich kollidiert sind die einzelnen Quarks und Gluonen, die sich in dem Proton befinden. Sich diesen Punkt vor Augen zu führen ist für das weitere Verständnis sehr wichtig: der LHC kollidiert eigentlich keine Protonen, er kollidiert Quarks und Gluonen (die gebunden sind zu einem komplexen Gebilde namens Proton). Für Quarks und Gluonen benutzt man oft das Wort „Partonen“, welches ich auch im Folgenden öfters verwenden werde. Ein Bindungszustand aus mehreren Partonen nennt man ein „Hadron“. Parton bedeutet also nichts anders als „Quark oder Gluon“, Hadronen sind Teilchen die aus diesen zusammengesetzt sind, wie z.B. Protonen oder Neutronen. Wir wollen nun herausfinden wie viele und welche Partonen denn in so einem Proton drinnen sind.
Die typische physikalische Größe die man an solchen Teilchenbeschleunigern misst sind sog. Wirkungsquerschnitte σ. Ohne uns hier zu sehr um die genau Definition zu kümmern kann man einfach sagen dass das in etwa einer Wahrscheinlichkeit entspricht die uns sagt, wie oft ein bestimmter Prozess in so einer Kollision auftritt. Diese Größe kann man für die verschiedensten Prozesse experimentell gut messen (denn die Experimentatoren wissen ja wie viele Teilchen sie zur Kollision bringen und sehen in ihren Detektoren wie oft sie welches Ergebnis erhalten), und es ist die Aufgabe der Theoretiker diese Wahrscheinlichkeiten möglichst genau zu berechnen um dann aus dem Vergleich mit dem Experiment Schlüsse ziehen zu können. Sagen wir wir wollen die Wahrscheinlichkeit berechnen dass irgendein Endzustand X in einer Proton-Proton Kollision produziert wird, wobei jedes der Protonen den Impuls K trägt, welcher durch den Teilchenbeschleuniger festgelegt ist. Das X kann hier für alles mögliche stehen, ein Higgs-Boson, ein Z-Boson, eine bestimmte Anzahl an Teilchenjets,… . Nennen wir diese Größe σ(P(K)+P(K)→X). Das ist etwas was die experimentellen Physiker anhand der Teilchen, die sie in ihren Detektoren nachweisen, messen können.
Jetzt wollen wir sehen wie wir diese Größe theoretisch berechnen können. Denn ohne eine theoretische Vorhersage, mit der wir unsere Messdaten vergleichen, können wir die experimentellen Ergebnisse nicht interpretieren. Doch unsere Rechenmethoden zur Beschreibung von Teilchenkollisionen taugen überhaupt nicht um so einen Prozess direkt zu berechnen, die Theoretiker versagen hier total. Sie sind nämlich nur gut darin Kollisionen von einzelnen hochenergetischen Elementarteilchen zu berechnen. Doch Protonen sind wie wir wissen keine fundamentalen Elementarteilchen, sondern bestehen ja aus Quarks, und für derart komplexe Gebilde sind unsere Rechenmethoden absolut nicht geeignet. Um dieses Problem zu umgehen geht man nun wie folgt vor: Zunächst macht man sich das Leben ein bisschen einfacher und berechnet den gewünschten Prozess, nur statt für eine Proton-Proton Kollision für eine Parton-Parton Kollision. Also anstatt σ(P(K)+P(K)→X) (den hadronischen Wirkungsquerschnitt) rechnen wir σ(p1(k1)+p2(k2)→X) (den partonischen Wirkungsquerschnitt) aus, wobei p1 und p2 zwei Partonen, also Quarks oder Gluonen, sind. Also den Wirkungsquerschnitt dafür dass in einer Kollision eines Partons der Sorte p1 (wobei p1 für ein beliebiges Quark oder Gluon stehen kann) mit Impuls k1 mit einem Parton der Sorte p2 (wobei p2 für ein beliebiges Quark oder Gluon stehen kann) mit Impuls k2 der gewünschte Endzustand X produziert wird. Das kann man meist sehr gut, auch wenn diese Rechnungen immer noch aufwändig und komplex sind.
Die Impulse k1 und k2 der Partonen die hier kollidieren sind natürlich nicht komplett unabhängig vom gesamten Impuls K den die Protonen tragen. In einem hochenergetischen Proton finden wir natürlich eher hochenergetische Partonen als in einem langsameren Proton. Es macht also Sinn die Impulse der Partonen zu jenen der Protonen in Beziehung zu setzen. Das macht man ganz einfach damit dass man weiß dass jedes der einzelnen Partonen in einem Proton natürlich nur einen Teil des gesamten Impuls tragen kann, und diesen Impulsanteil nennen wir x. Wir können für den Impuls eines Partons in einem Proton mit Gesamtimpuls K also auch schreiben als xK, wobei x eine Zahl zwischen 0 und 1 ist und der Anteil dieses Partons am Gesamtimpuls des Protons ist. Die Impulse k1 und k2 der beiden kollidierenden Partonen schreiben wir also als x1K und x2K.
Um den vollen Prozess P(K)+P(K)→X korrekt zu beschreiben müssen wir nun über alle Möglichkeiten für so einen partonischen Prozess p1(x1K)+p2(x2K)→X summieren. Es könnte ja sein dass ein Up Quark aus dem einen Proton mit einem Up Quark aus dem anderen Proton kollidiert. Oder ein Down Quark aus dem einen Proton mit einem Gluon aus dem anderen, usw. … . Wir müssen also über alle möglichen Kombinationen der verschiedenen Arten von Partonen summieren. Denn wenn wir ein Proton mit einem anderen Proton kollidieren könnte ja jede von diesen Kombinationen auch eintreten. Des weiteren könnte das Parton aus dem einen Proton einen Impulseinteil von 10% des Gesamtimpulses tragen und das Parton aus dem anderen Proton einen Impulsanteil von 30%. Oder das eine 4.25% und das andere 0.12%, usw. … . Auch hier müssen wir natürlich alle möglichen Kombinationen berücksichtigen, also über alle möglichen Werte von x1 und x2 integrieren (wer mit Integralen nicht so vertraut ist soll sich ein Integral einfach als eine Summe vorstellen. Es ist eh genau dasselbe nur halt für eine kontinuierliche Variable statt einer diskreten. Also wann immer irgendwo ein Integral steht bedeutet dass einfach wieder nur dass wir über alle möglichen Werte die diese Variable annehmen kann summieren).
Damit sind wir schon fast am Ziel, aber eine entscheidende Sache fehlt noch: wir müssen berücksichtigen wie oft denn jeder dieser möglichen Prozesse tatsächlich auftritt. Vielleicht ist es ja viel wahrscheinlicher ein Up Quark in einem Proton zu treffen als ein Down Quark. Dann müssten wir alle Prozesse bei denen ein Up Quark vorkommt natürlich entsprechend höher gewichten in unserer Summe über alle möglichen Prozesse. Dasselbe gilt für die verschiedenen Impulsanteile welche die Partonen tragen können. Wer sagt uns denn dass die alle gleich wahrscheinlich sind? Wiederum könnten manche häufiger vorkommen als andere, was wir wiederum in der Gewichtung der einzelnen partonischen Prozesse die wir berechnen berücksichtigen müssen. Wir müssen also noch etwas in unsere Rechnung mit den einzelnen partonischen Kollisionen hinein stecken, um am Ende des Tages die volle Protonen Kollision korrekt beschreiben zu können. Nämlich eine gewissen Gewichtung die uns sagt wie wahrscheinlich es ist dass eine Kollision von zwei bestimmten Partonen aus den beiden Protonen mit einem bestimmten Impuls tatsächlich stattfindet. Also die Wahrscheinlichkeit dafür in einem Proton ein Parton der Sorte p mit Impulsanteil x zu finden. Nennen wir diese Wahrscheinlichkeit fp(x).
Alles zusammen genommen bedeutet das also: Um den Wirkungsquerschnitt einer Proton-Proton Kollision σ(P(K)+P(K)→X) zu berechnen (was man nicht direkt kann), nehme man den Wirkungsquerschnitt einer Parton-Parton Kollision σ(p1(x1K)+p2(x2K)→X) (welchen man zum Glück schon berechnen kann), summiert über alle möglichen Kombinationen von Partonen und Anteile der Partonen am Gesamtimpuls des Protons und gewichtet dabei alles mit der jeweiligen Wahrscheinlichkeit fp(x) eben dieses Parton mit eben diesem Impulsanteil auch wirklich im Proton zu finden.
Gießen wir nun alles was hier im letzten Absatz beschrieben wurde in eine Formel, so lautet diese
wobei die Summe über alle Arten von Quarks, Antiquarks und Gluonen läuft.
Von dieser Formel braucht man sich nicht abschrecken lassen, sie ist ganz einfach nur der mathematische Ausdruck dessen was oben in Worten beschrieben ist. Und so nebenbei ziemlich die wichtigste Formel in der Physik an Hadronen Collidern überhaupt. Ohne sie geht hier gar nichts. Wer diese Formel schon einmal gesehen und verstanden hat, der hat bereits einen gewaltigen Schritt zum Verständnis der echten Physik an Teilchenbeschleunigern gemacht. Ein zentraler Bestandteil dieser Formel sind die Wahrscheinlichkeiten fp(x), die uns sagen wie die einzelnen Partonen im Proton verteilt sind, uns also tatsächlich etwas über die innere Struktur des Protons verraten. Wir werden uns mit diesen Funktionen fp(x) im Folgenden noch eingehender beschäftigen. Sie tragen den etwas sperrigen Namen „Parton-Verteilungsfunktionen“, ich werde sie im Folgenden öfters mit PDF (parton distribution function) abkürzen.
Kommen wir nun zurück zu der Frage nach dem Aufbau eines Protons. Der entscheidende Punkt ist nämlich der: es gibt nicht nur PDFs für Up und Down Quarks und Gluonen. Nur damit allein könnte man die experimentellen Daten niemals korrekt beschreiben, es würde immer etwas fehlen. Man benötigt auch die PDFs für Strange Quarks1 und auch alle Antiquarks um vernünftige Ergebnisse zu bekommen. Das bedeutet auch das Strange Quark, das seinem Namen nach ja als etwas sehr seltsames gesehen wird, findet man in einem ganz normalen Proton. Das bedeutet außerdem die Wahrscheinlichkeit ein Antiquark in einem Proton zu treffen (von dem man meinen möchte es hat überhaupt nichts mit Antimaterie zu tun) ist größer als null.
Parton-Verteilungsfunktionen: Warum ein Proton irgendwie doch wieder aus drei Quarks besteht, aber eigentlich ja doch nicht
Wie wir gesehen haben spielen die PDFs – die Wahrscheinlichkeit ein bestimmtes Parton mit einem bestimmten Impuls im Proton zu finden – also eine ganz entscheidende Rolle. Sie sind es die die gesamte relevante Information über die innere Struktur des Protons beinhalten. Eine genaue Kenntnis dieser Funktionen ist essenziell für jede Berechnung die wir für so eine Teilchenkollision anstellen wollen. Genau das, nämlich diese PDFs so genau wie möglich zu bestimmen, ist aber gar nicht so einfach. Wir können die PDFs nämlich bis heute gar nicht berechnen. Nicht dass es ein prinzipielles Problem in der Theorie wäre, wir schaffen es einfach nur noch nicht weil es zu komplex ist. Also irgendwann mit Fortschritten in unseren numerischen Rechenmethoden wird es vielleicht einmal gehen, aber heute eben noch nicht. Woher haben wir nun also diese Funktionen, die ja ein essenzieller Input für jede theoretische Vorhersage für Prozesse an Hadronen Collidern sind? Aus dem Experiment. PDFs, also quasi die innere Struktur von Protonen, werden in Streuexperimenten an Protonen gemessen. Meist verwendet man dazu die Daten aus tief-inelastischer Elektron-Proton-Streuung, die wichtigsten Daten zur Bestimmung der PDFs sind heute immer noch die des ehemaligen Teilchenbeschleunigers HERA am DESY in Hamburg, der seit den 90er Jahren bis zum Jahr 2007 in Betrieb war.
Sehen wir uns also nun ein paar Eigenschaften der PDFs und was wir daraus lernen können genauer an. Wenn f(x) die Verteilung der Partonen nach dem Impulsanteil x beschreibt, und wir diese Verteilung mit eben diesem Impulsanteil x multiplizieren, dann erhalten wir die Impulsverteilung xf(x) der Partonen im Proton. Integriert man über alle möglichen Impulsanteile von 0 bis 1 (d.h. man summiert über alle Möglichkeiten welchen Impuls so ein Parton haben kann) so erhält man den Anteil den die Partonen dieser Sorte am Gesamtimpuls des Protons tragen
Wenn man das tut dann erhält man als Ergebnis dass die Up und Down Quarks im Proton in etwa 30% des Impulses tragen2. Das widerspricht schon ziemlich klar der Vorstellung dass ein Proton nur aus Up und Down Quarks besteht. Nehmen wir außerdem noch die Gluonen hinzu, so kommen wir immerhin auf ungefähr 80%. Da fehlt aber offensichtlich immer noch was. Erst wenn man die Impulsanteile aller verschiedener Partonen zusammen zählt, inklusive Strange Quarks und aller möglichen Antiquarks, erhalten wir in Summe den Gesamtimpuls des Protons
Diese Formel ist nur der Ausdruck dessen dass die Summe der Impulse aller Teilchen in einem Proton genau den gesamten Impuls des Protons ergeben muss – ist ja logisch. Sie geht aber wie gesagt nur auf wenn man wirklich alle Partonen in der Summe berücksichtigt. Nur mit Up und Down Quarks und auch Gluonen fehlt ganz klar etwas. Man findet eben tatsächlich immer auch ein bisschen Antimaterie in einem Proton, wenn man nur tief genug hinein blickt.
Die Impulsverteilungen xf(x) sind in nachfolgender Abbildung gezeigt.
![Impulsverteilung xf(x) der Partonen. Die zur Erstellung dieser Abbildung verwendeten PDF Sets stammen von: A. D. Martin, W. J. Stirling, R. S. Thorne and G. Watt, "Parton distributions for the LHC", Eur. Phys. J. C 63 (2009) 189-285, arXiv:0901.0002 [hep-ph]](https://scienceblogs.de/astrodicticum-simplex/files/2018/09/PDFplot-500x275.png)
Impulsverteilung xf(x) der Partonen. Die zur Erstellung dieser Abbildung verwendeten PDF Sets stammen von: A. D. Martin, W. J. Stirling, R. S. Thorne and G. Watt, “Parton distributions for the LHC”, Eur. Phys. J. C 63 (2009) 189-285, arXiv:0901.0002 [hep-ph]
Hier sieht man dass eigentlich nicht die Quarks, sondern die Gluonen den wichtigsten Anteil tragen. Außerdem sieht man dass die Wahrscheinlichkeit viel größer ist ein Parton mit einem sehr niedrigen Impulsanteil zu treffen als eines mit einem sehr hohen (d.h. man sieht dass die Verteilungen für kleine x alle viel höher sind als für große). Das bedeutet dass die eigentliche Kollisionsenergie (nämlich die zwischen den einzelnen Partonen) in so einem Teilchenbeschleuniger meist deutlich unter der Gesamtenergie der Protonen liegt die wir kollidieren. Auch wenn die Schwerpunktsenergie der Protonen am LHC 13 TeV beträgt, so ist es schon sehr sehr selten dass wir tatsächlich Kollisionsenergien der Partonen (und das ist die eigentlich relevante Größe) von 1 TeV oder mehr erhalten.
Kehren wir nun zurück zu der Frage wie viele Quarks denn in einem Proton wirklich sind. So wie wir mit dem Integral über alle möglichen Werte der Impulsverteilung xf(x) den gesamten Impulsanteil einer Partonensorte erhalten haben, so erhalten wir über das Integral über alle möglichen Werte der Parton-Verteilungsfunktion f(x) selbst die gesamte Anzahl der Partonen dieser Sorte im Proton. Das kann man nun versuchen auszurechnen, wird dabei allerdings feststellen dass man dabei für alle PDFs in das selbe Problem läuft. Dieses Integral ist nämlich divergent
Das sagt uns dass die Frage nach der Anzahl der Quarks in einem Proton leider keine Antwort hat, beziehungsweise dass die Frage selbst damit eigentlich nicht sinnvoll ist. Die Anzahl der Quarks in einem Proton hat keinen definierten Wert („unendlich“ ist keine sinnvolle Größe)! Diese Antwort mag unbefriedigend wirken, es ist aber nun mal so. Dabei könnten wir es jetzt bleiben lassen und diese Antwort als undefiniert stehen lassen (und das ist wie gesagt auch wirklich die korrekte Antwort), wir können allerdings noch etwas anderes ausprobieren. Wir können nämlich versuchen zumindest so etwas wie eine „netto“ Anzahl an Quarks in einem Proton zu ermitteln, wenn wir diese als die Anzahl der Quarks minus der Antiquarks definieren. Diese netto Größe wird normalerweise als Valenzquarks bezeichnet und ergibt sich somit zu
wobei der Strich über dem q bezeichnen soll dass es sich hier um die zugehörige Antiquark-PDF zum Quark der Sorte q handelt. Ich habe hier bewusst q (für Quark) statt p (für Parton) geschrieben, da sich diese Größe nur für Quarks und nicht für Gluonen (die keine Antiteilchen haben) definieren lässt. Wie wir bereits wissen ist sowohl die Anzahl der Quarks als auch die Anzahl der Antiquarks für sich allein nicht definiert, aber manchmal erhält man etwas Sinnvolles wenn man die Differenz zweier divergenten Größen nimmt. Und so ist es auch hier. Man kann nämlich nun diese netto Zahl für u, d und s Quarks ausrechnen und erhält dafür in der Tat einen endlichen Wert. Und hier passiert etwas Interessantes, für diese netto Quark Zahlen in einem Proton3 erhält man nämlich
Und hier haben wir nun den Kreis geschlossen zu dem ersten Satz dieses Artikels, den wir ja eigentlich widerlegen wollten. Ja, ein Proton besteht aus zwei Up und einem Down Quark – in Summe zumindest, irgendwie 😉
________________________________________________________________
1Bei hohen Energien definiert man, aus sagen wir mal „rechentechnischen Gründen“, auch effektive PDFs für die schweren Charm und Bottom Quarks. Aber hier ist die Sache dann nochmal ein wenig anders und wird daher von mir jetzt einfach mal ignoriert.
2Ich habe hier unterschlagen dass die PDFs eigentlich auch von der (partonischen) Kollisionsenergie abhängen. Die hier zitierten Werte und auch Abbildungen sind für eine Energie von 125 GeV.
3Für ein Antiproton oder ein Neutron würden natürlich andere Zahlen rauskommen. Es kann sich jeder selbst überlegen welche.

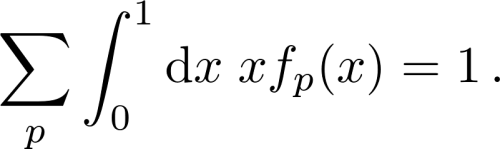
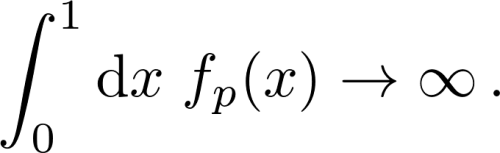
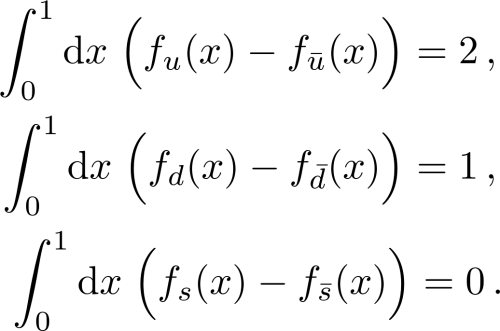










Kommentare (17)