 Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video.
Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video.
Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]
Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.
—————————————————————————————
Sternengeschichten Folge 353: Kalte Fusion
Es war lange Zeit nicht klar, wie und auf welche Weise unsere Sonne und die anderen Sterne leuchten. Über all die Irrtümer auf diesem Weg mache ich irgendwann mal vielleicht eine eigene Folge. Aber mittlerweile wissen wir recht gut, woher die Sonne ihre Energie bekommt und ich habe darüber in den Folgen 168 und 169 der Sternengeschichten im Detail gesprochen. Dort, so wie im Inneren aller anderen Sterne, findet Kernfusion statt. Das heißt, dass leichte Atome miteinander verschmelzen um schwerere Atome zu bilden wobei Energie frei wird. Bei Sternen wird hauptsächlich Wasserstoff zu Helium fusioniert; aber auch andere Fusionsreaktionen sind möglich.
Dass in den Kernen von Atomen jede Menge Energie steckt, wissen wir seit Albert Einstein seine berühmet Formel E=mc² aufgestellt hat. Die Protonen und Neutronen im Kern werden durch Kernkräfte zusammengehalten, ein Atomkern braucht also eine gewisse Bindungsenergie. Die ist unterschiedlich groß, je nachdem wie viele Protonen und Neutronen einen Kern bilden. Am stärksten ist die Bindung bei bestimmten Eisen- und Nickel-Atomen; alle anderen Atomkerne haben eine geringere Bindungsenergie. Jetzt kommt Einsteins Formel ins Spiel: Energie und Masse sind äquivalent, das eine kann in das andere umgewandelt werden. Oder anders gesagt: Zählt man die Masse der einzelnen Protonen und Neutronen eines Atomkerns zusammen, dann ist das Resultat immer größer als die Gesamtmasse des Atomkerns. Die fehlende Masse steckt in der Bindungsenergie, die die Kernbausteine zusammenhält.
Atomkerne die schwerer sind als Eisen setzen Energie frei, wenn man sie spaltet und zu leichteren Atomen macht. Atomkerne die leichter als Eisen sind muss man zu schwereren Atomkernen fusionieren, um überschüssige Bindungsenergie freizusetzen. Beide Vorgänge können in der Natur auftreten. Es gibt viele Atomkerne, die instabil sind und im Laufe der Zeit zerfallen. Das nennen wir “Radioaktivität” und die dabei freiwerdende Energie in Form von Strahlung kann unter Umständen gefährlich werden. Die Spaltung von Atomkernen haben wir aber auch künstlich hergestellt. Einerseits unkontrolliert, in Atomwaffen; andererseits unter Kontrolle in Kernkraftwerken, wo wir die Spaltung von Atomen absichtlich herbeiführen um daraus Energie zu erzeugen.
Aber schon bevor die ersten Atomwaffen und Kernkraftwerke gebaut wurden, wusste man, dass man bei Kernfusion wesentlich mehr Energie erzeugen kann als bei der Kernspaltung. Und man wusste, dass genau dieser Fusionsprozess auch in den Sternen stattfinden. Warum also nicht probieren, die Kernfusion auch künstlich zu produzieren und die Energie zu nutzen?
Das Problem an der Sache: Die Kernspaltung ist vergleichsweise einfach. Man muss eigentlich nur einen schweren Atomkern mit einem ausreichend schnellen Teilchen beschießen und dann bricht er auseinander. In der Praxis war es natürlich sehr viel kniffliger, aber man hat es dann doch in erstaunlich kurzer Zeit hinbekommen, wirtschaftlich nutzbare Energie durch Kernspaltung zu erzeugen. Bei der Kernfusion war man anfangs ebenso optimistisch. Hier ist es aber viel schwerer. Denn Atome wollen normalerweise nicht miteinander fusionieren. Die Atomkerne stoßen einander ab und nur wenn sie sehr schnell sind, kann ihre Bewegungsenergie die Abstoßung überwinden. Nur dann kommen sie sich nahe genug, dass die innerhalb des Kerns wirkenden Kräfte dominieren und die Kerne sich miteinander verbinden.
Will man Atome schnell machen, muss man sie erhitzen. In einem Stern wie der Sonne sind dafür Temperaturen von weit mehr als 10 Millionen Grad nötig! Die gibt es dort nur im Zentrum; in den äußeren Bereichen ist es kühler und dort findet auch keine Kernfusion statt. Ein Stern ist ein recht simpler Kernfusionsreaktor: Er besteht – vereinfacht gesagt – aus einem gewaltigen Haufen Wasserstoff der sich in seinem Zentrum unter seinem eigenen Gewicht so stark verdichtet, dass die entstehenden hohen Temperaturen ausreichen damit Kernfusion einsetzt. Die Energie wird explosiv und unkontrolliert frei; die Sonne ist quasi eine gigantische, andauernde Explosion die von ihrer eigenen Gravitationskraft zusammengehalten wird. So etwas können wir auf der Erde natürlich nicht nachbauen. Aber auch hier braucht man die gleichen hohen Temperaturen. Es gibt allerdings kein Material, dass bei mehr als 10 Millionen Grad nicht sofort gasförmig wird; worin also soll man die Wasserstoffatome aufbewahren, während sie fusionieren? Das geht nur indem man sie mit Magnetfelder einfängt, was bei weitem nicht so einfach ist wie es klingt. Man muss natürlich auch haufenweise Energie aufwenden um den Wasserstoff entsprechend stark aufzuheizen damit er überhaupt fusionieren kann und wenn man mehr Energie braucht als am Ende rauskommt bringt es auch nichts. Man kann auch nicht einfach irgendeinen Wasserstoff nehmen sondern nur spezielle Variationen die auch nicht leicht zu kriegen oder produzieren sind. Man braucht Deuterium und Tritium, Isotope des Wasserstoffs; ich werde aber im Weiteren trotzdem immer von “Wasserstoff” sprechen damit es nicht noch verwirrender wird. Man hat es noch geschafft die Kernfusion in Form von Wasserstoffbomben als explosive Energiefreisetzung zu verwenden, aber an einer kontrollierten Kernfusion mit der wirtschaftlich Energie produziert wird arbeitet man ohne Erfolg seit der Mitte des letzten Jahrhunderts.
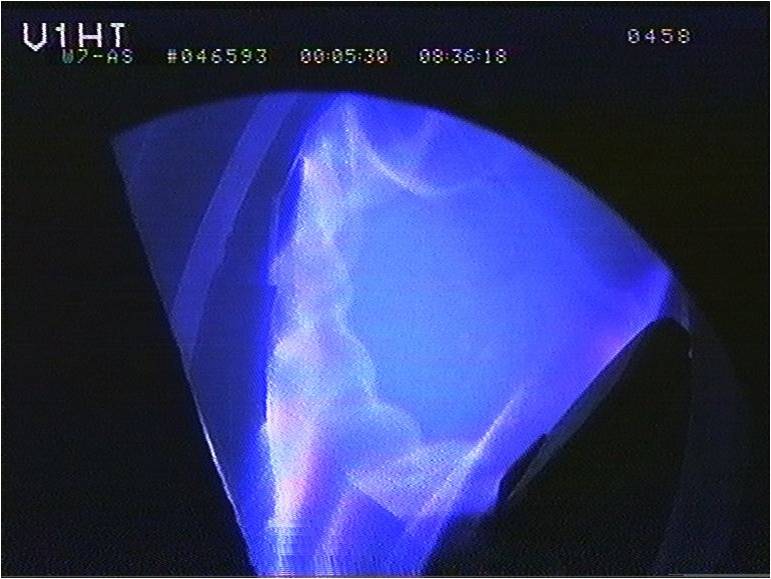
Blick auf das Plasma in einem Fusionsreaktor ; hier Wendelstein 7-AS (Bild: W7-AS Team, J. Baldzuhn, CC-BY-SA 3.0)
Welche Methoden es da gibt, welche Probleme dabei auftreten und ob man die Kernfusion doch noch einmal nutzen wird können sind alles Themen für andere Folgen der Sternengeschichten. Heute geht es um eine verlockende Abkürzung: Was, wenn man die hohen Temperaturen gar nicht braucht und damit die ganzen Probleme gar nicht erst hat. Kann man nicht auch eine “kalte Fusion” machen?
Kann man! Zum Beispiel mit Myonen. Ein Myon ist ein Elementarteilchen; eigentlich nichts anderes als ein Elektron nur schwerer. Und instabil; ein Myon lebt nur ein paar Sekundenbruchteile bevor es wieder zerfällt. In der Zeit kann es aber bei der Kernfusion helfen. Normalerweise wird ein Atomkern ja von Elektronen umkreist. Der Atomkern ist elektrisch positiv geladen; die Elektronen sind negativ und insgesamt ist ein Atom elektrisch neutral. Kommen zwei Atome sich nahe, stoßen sich aber die jeweils negativ geladenen Hüllen ab; die Elektronen stören überhaupt sehr bei der Kernfusion. Sie verschwinden aber auch, wenn die Temperaturen hoch genug sind. Bzw. verschwinden nicht, aber lösen sich vom Atomkern. In der Sonne fusionieren nur die Kerne und auch bei den Versuchen auf der Erde verwendet man nur Atomkerne ohne Elektronen – muss sie dann aber eben enorm aufheizen, damit die positiv geladenen Kerne ihre wechselseitige Abstoßung überwinden können.
Die Sache mit den Myonen und der kalten Fusion läuft nun aber anders und – sehr vereinfacht – so ab: Unter bestimmten Umständen kann ein Atomkern anstatt eines Elektrons ein Myon einfangen. Myonen unterscheiden sich ja nur durch ihre größere Masse von den Elektronen und sind ebenfalls negativ geladene. Weil sie aber so viel schwerer sind, umkreisen sie den Atomkern auch sehr viel enger. Und weil so die elektrisch negative Ladung sehr viel dichter an der positiven Ladung des Kerns ist, kann sie die Ladung besser abschirmen. Anders gesagt: Ein Atomkern mit Myon “spürt” andere Atomkerne weniger stark und kann leichter mit ihnen fusionieren. Schon in den 1960er Jahren gelang es, mit Myonen Kernfusion ohne hohe Temperaturen durchzuführen. Aber damit das ganze wirtschaftlich brauchbar wird, muss der Prozess dauerhaft ablaufen können. Man braucht eine Kettenreaktion, bei der immer neue Myonen freigesetzt werden, die immer neue Fusionen ermöglichen. Das passiert aber nicht, weil die Myonen zu schnell zerfallen. Und wenn man künstlich von außen Myonen zusetzen will, ist die Energie die für die Produktion der Myonen nötig ist so groß, dass der ganze Prozess mehr Energie verbraucht als freigesetzt wird. Kalte Fusion mit Myonen ist also möglich, kann aber nicht zur Energiegewinnung benutzt werden.
Aber wenn man die Atomkerne mit Myonen zur Fusion bei niedrigen Temperaturen überreden kann, dann ja vielleicht auch irgendwie anders? Am 23. März 1989 hielten die beiden Chemiker Martin Fleischmann und Stanley Pons eine Pressekonferenz ab. Sie waren nicht einfach irgendwelche Spinner, sondern jeweils sehr angesehene Wissenschaftler ihrer Fachgebiete. Deswegen hörten auch alle aufmerksam zu, als sie davon erzählten, wie sie Wasserstoffatome miteinander fusioniert hätten und zwar bei niedrigen Temperaturen, in einem simplen Gerät das man in jedem Labor aufstellen kann. Der Schlüssel zum Erfolg sei das Metall Palladium: Von allen chemischen Elementen kann es am meisten Wasserstoff aufnehmen: Bei Raumtemperatur kann es das 900fache seiner eigenen Masse an Wasserstoff an sich binden. Vermutlich, so Fleischmann und Pons, würden die Wasserstoffatome im Palladium – wieder sehr vereinfacht gesagt – auf so engem Raum konzentriert, dass sie miteinander fusionieren können. Dass ihr Prototyp tatsächlich Energie durch Kernfusion produziert wollten sie durch die freiwerdenen Helium-Atome (zu denen der Wasserstoff verschmilzt), die ebenfalls freiwerdenden Neutronen und ein wenig überschüssige Wärme nachgewiesen haben.
Es war eine prinzipiell plausible Behauptung seriöser Wissenschaftler. Nur dass sie per Pressekonferenz bekannt gegeben wurde anstatt durch eine Veröffentlichung in der Fachliteratur war ungewöhnlich. Denn ohne genau Daten und eine exakte Beschreibung der Methoden war es schwer, das ganze zu prüfen. Aber schon bald fanden genau solche Prüfungen statt; andere Arbeitsgruppen wiederholten die Experimente und stellten fest, dass die kalte Fusion von Fleischmann und Pons nicht funktioniert. Sie hatten ein paar Fehler gemacht; ein paar Kontrollexperimente nicht gut genug durchgeführt und Daten nicht korrekt interpretiert. Das alles wäre rein prinzipiell nicht weiter tragisch gewesen. So was kommt vor in der Wissenschaft. Hypothesen, Theorien und Ergebnisse werden veröffentlicht; sie werden geprüft und manchmal werden sie eben auch widerlegt. Fleischmann und Pons aber wollten ihren Fehler nicht akzeptieren und weigerten sich den Befund der wissenschaftlichen Gemeinschaft anzuerkennen. Das allerdings ist tragisch, vor allem bei einem so wichtigen Thema wie der Kernfusion. Das war nicht einfach irgendein abstraktes wissenschaftliches Ergebnis; das hätte potentiell die ganze Welt verändern können. Medien waren enorm interessiert; ebenso wie die Politik und die Wirtschaft. Und es gab eine Riesenwirbel, der eine nüchterne Betrachtung der Sachlage schwer machte.

Fusionsbomben sind leicht. Leider… (Bild: NNSA, gemeinfrei)
An kalter Fusion wird aber immer wieder mal geforscht. Durchaus auch erfolgreich. Zum Beispiel im Fall der “Pyrofusion”. Dabei nutzt man starke elektrische Felder um Wasserstoffatome an der Spitze einer Nadel zusammenzudrängen und zur Fusion zu bringen. Das funktioniert, braucht aber immer mehr Energie als freigesetzt werden kann. Nicht funktioniert hat dagegen ie “Sonofusion”, bei der amerikanische Wissenschaftler Fusion durch Schallwellen erreichen wollten. Dabei geht es darum, quasi kleine Hohlräumen, winzige Bläschen in einer Flüssigkeit zu erzeugen, in denen ein Vakuum herrscht. Die Blasen kollabieren enorm schnell, erzeugen dabei kurzfristig sehr hohe Temperaturen bei denen Kernfusion stattfinden kann. Aber so wie bei Fleischmann und Pons konnten auch diese Ergebnisse nicht bestätigt werden und auch hier weigerte sich der beteiligte Wissenschaftler – Rusi Taleyarkhan vom Oak Ridge National Laboratory – seinen Fehler anzuerkennen.
Die kalte Fusion bleibt weiterhin verlockend. Energie zu produzieren, ohne große Maschinen, ohne extreme Temperaturen, billig, einfach und in enormer Menge. Das klingt zu schön um wahr zu sein und auch wenn sich die Wissenschaft immer noch mit dem Thema beschäftigt, ist es mit an Sicherheit grenzender Wahrscheinlichkeit auch nicht wahr. Wenn wir Energie durch Kernfusion gewinnen wollen, werden wir dafür die gewaltigen Geräte brauchen, die mit enorm hohen Temperaturen arbeiten. Und müssen all die Probleme lösen, die sich dadurch ergeben. Ob uns das gelingen wird, ist aber wieder eine ganz andere Frage und eine ganz andere Geschichte.












Kommentare (35)