 Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]
Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.
—————————————————
Sternengeschichten Folge 440: Die Gravitationskonstante
Ohne Gravitation geht nichts im Universum. Vor allem in der Astronomie, wo es ja meistens um sehr massereiche Objekte wie Sterne oder Planeten geht, kommt man ohne Gravitation nicht aus. Wenn man das Universum in seiner Gesamtheit verstehen will, braucht man die Gravitation. Man braucht sie auch, wenn man alles andere verstehen will – immerhin ist die Gravitation eine der vier fundamentalen Kräfte der Natur. Und wenn man wissen will, wie eine Kraft funktioniert, dann muss man natürlich auch wissen, wie stark sie ist.
Wir alle haben in der Schule von Newtons Gravitationsgesetz gehört. Im 17. Jahrhundert hat Isaac Newton festgestellt, dass die Gravitationskraft zwischen zwei Objekten proportional zu den Massen der beiden Objekte ist und indirekt proportional zum Quadrat ihres Abstandes. Aber wir wollen ja wissen, wie stark die Kraft genau ist. Das mit dem “proportional” heißt in dem Fall ja nur: Wenn die Masse der Objekte größer wird, wird die Gravitationskraft im gleichen Ausmaß größer. Und wenn der Abstand größer wird, dann sinkt die Kraft und zwar nicht im gleichen Ausmaß, sondern schneller (weil sie ja zum Quadrat des Abstands proportional ist). Das zu wissen ist gut, wenn man prinzipiell verstehen will, wie die Gravitationskraft funktioniert. Aber wenn man konkret berechnen will, wie stark die Kraft ist – zum Beispiel weil man wissen will, wie sich die Himmelskörper bewegen und wohin sie sich bewegen – dann reicht das “proportional” nicht. Deswegen findet man in Newtons Gravitationsgesetz auch noch eine Zahl, eine “Proportionalitätskonstante”. Die exakte Formel lautet: Gravitationskraft ist gleich Masse eins mal Masse zwei, geteilt durch den Abstand zum Quadrat und das ganze nochmal multipliziert mit G.
Womit wir jetzt beim Thema dieser Folge sind: G. Das ist die Gravitationskonstante. Es ist eine Naturkonstante und sie sagt uns, wie stark die Gravitationskraft ist. Ohne den genauen Zahlenwert von G zu kennen, können wir keine Gravitationskräfte zwischen Objekten berechnen. Das gilt übrigens nicht nur für die Formel von Isaac Newton. Seit 1915 haben wir ja eine neue, bessere Beschreibung der Gravitation von Albert Einstein, die allgemeine Relativitätstheorie. Und auch in diesen Formeln finden wir G. Was auch sonst; diese Zahl muss immer auftauchen, wenn es um Gravitation geht.
Aber schauen wir nochmal zurück ins 17. Jahrhundert, zu Isaac Newton. Als er damals seine Formel zur Gravitation aufgestellt hat, war ihm natürlich klar, dass er dafür die Zahl braucht, mit der man die Stärke der Gravitation angibt. Er konnte sie damals aber nicht bestimmen; es gab keine Messgeräte dafür und er konnte sie nur schätzen. Das reicht in der Wissenschaft aber nicht, wenn es um Naturkonstanten geht, dann wollen wir die so exakt wie nur irgendwie möglich kennen. Das ist aber – gerade bei der Gravitationskonstante enorm schwer.
Der offiziell zur Verwendung empfohlene Wert – und ja, es gibt natürlich eine internationale Organisation die dafür zuständig ist, die jeweils besten bekannten Werte physikalischer Konstanten zu sammeln und zu bewerten, das “Committee on Data for Science and Technology (CODATA)” – dieser offizielle Wert für die Gravitationskonstante beträgt 6,67430 mal 10 hoch minus 11 Kubikmeter pro Kilogramm pro Sekunde zum Quadrat. Sicher ist man sich aber nur beim 6,674-Teil dieser Zahl, schon die nächsten Stellen sind nicht mehr genau, da könnte es auch mit 2 oder 4 weitergehen. Und das ist schon ein wenig unangenehm. Wenn man sich die anderen Naturkonstanten anschaut – den Wert der Lichtgeschwindigkeit, die Masse eines Elektrons, das Plancksche Wirkungsquantum, und so weiter – dann kennen wir sie entweder exakt oder zumindest sehr, sehr, sehr genau. Nur bei der Gravitation kriegen wir immer noch nicht mehr als zwei, drei sichere Stellen hinter dem Komma hin.
Das liegt natürlich einerseits daran, dass die Gravitation eine enorm schwache Kraft ist. Das klingt ein wenig widersprüchlich – ist es aber gar nicht. Ich kann problemlos ein bis zwei Meter hoch in die Luft springen (je nach körperlicher Leistungsfähigkeit), obwohl die GESAMTE ERDE mit der Gravitationskraft ihrer Masse an mir zieht und mich zurück halten will. Ich kann eine Postkarte mit einem simplen, kleinen Magnet an meinem Kühlschrank befestigen und sie wird nicht zu Boden fallen. Die elektromagnetische Kraft des winzigen Magnet reicht aus, um der Gravitationskraft eines ganzen Planeten dauerhaft entgegen zu wirken. Von allen vier fundamentalen Kräften der Natur – Elektromagnetismus, stark und schwache Kraft im Inneren der Atomkerne und Gravitation – ist die Gravitationskraft bei weitem und mit Abstand die schwächste Kraft. Sie spielt im Universum nur deswegen eine so dominierende Rolle, weil dort eben auch sehr viele sehr massereiche Objekte wie Sterne, Galaxien, und so weiter zu finden sind. Die Schwäche der Kraft ist also das einerseits, wenn es darum geht, warum die Gravitationskonstante so schwer zu messen ist. Das “andererseits” ist ein wenig komplexer. Aber dazu kommen wir später noch.
Schauen wir uns zuerst einmal an, wie man die Gravitationskonstante überhaupt messen kann. Man kann es natürlich indirekt anstellen: Ich kann mir anschauen, wie sich ein Himmelskörper – zum Beispiel die Erde – um einen anderen – etwa die Sonne – bewegt. Wenn ich dann noch die Masse von Erde und Sonne bestimme und ihren Abstand messe, habe ich eigentlich schon alles, was man braucht. Aus der Bewegung kann ich die Kraft ableiten, die zwischen beiden wirken muss und mit den anderen bekannten Größen kann man dann die Gravitationskonstante berechnen. Das Problem: Es ist absolut nicht einfach, die Masse von Erde und Sonne oder ihren Abstand so exakt zu messen, dass man damit auch die Gravitationskonstante in der gewünschten Exaktheit zu berechnen. Dazu braucht man kleinere Massen und kleinere Abstände, die sich besser vermessen lassen. Aber da ist dann natürlich auch die wirkende Gravitationskraft wesentlich schwächer.
Der erste, der sich an einer direkten Messung der Gravitationskonstante versucht hat, war der britische Wissenschaftler Henry Cavendisch. Er hat es 1798 mit einem selbst erfundenen Instrument probiert, einer Gravitationswaage. Die Idee dahinter ist eigentlich simpel: Man nimmt zwei schwere Kugel, bei Cavendish waren sie knapp 1,5 Kilogramm schwer. Diese Kugeln sind verbunden, ein bisschen so wie eine Hantel und an einem Draht aufgehängt, so dass sich die ganze Konstruktion am Draht hängend drehen kann. Dann nimmt man zwei andere und schwerere Kugeln, die von außen und ein bisschen seitlich an die aufgehängten Kugeln herangeschoben werden können. Zwischen den großen und den kleinen Kugeln wirkt nun – wie zwischen allen anderen Objekten in diesem Universum eine Gravitationskraft. Die großen Kugeln ziehen die kleinen Kugeln an und verdrehen die Hantel ein kleines bisschen. Diese Verdrehung kann man messen und aus der Stärke der Verdrehung folgt – sofern man die Massen der Kugeln und ihren Abstand kennt – die Gravitationskonstante.
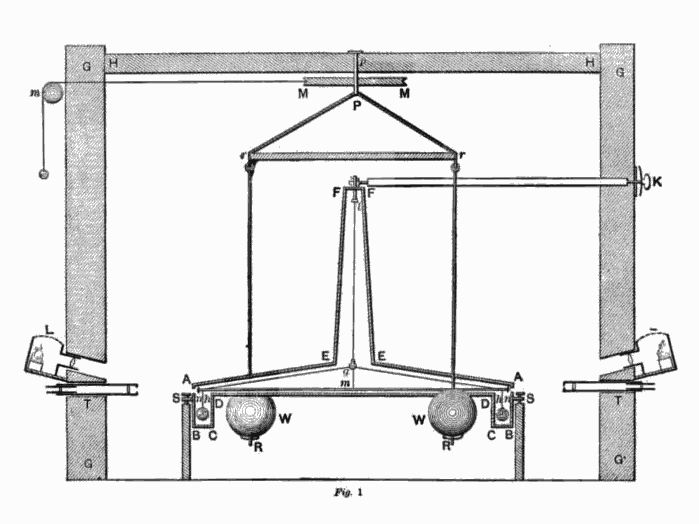
Die “Gravitationswaage” mit der Henry Cavendish 1798 die Gravitationskonstante gemessen hat (Bild: gemeinfrei)
Man kann sich vorstellen, wie knifflig es ist, so ein Experiment tatsächlich auszuführen. In der Theorie mag das ja alles gut funktionieren. In der Praxis aber nicht. Den bevor man anfangen kann, muss die Kugelhantel ja VÖLLIG ruhig an ihrem Draht hängen. Ein winziger Luftzug würde schon reichen, sie in Schwingung zu versetzen. Wenn ein paar hundert Meter weit weg ein Auto vorbei fährt und den Boden minimal erschüttert, würde der Draht zu schwingen anfangen. Und so weiter. Gut, mit Autos hatte Cavendish damals kein Problem. Aber auch ein vorbeilaufender Mensch, irgendwas das zu Boden fällt oder einfach nur jemand, der neben dem Experiment steht: All das würde die Messung enorm schwierig machen bzw. unmöglich. Cavendish hat den ganzen Aufbau daher in eine Kiste gepackt. Die Kiste hat er in einen Schuppen gestellt. Alles wurde verschlossen und dann hat er erstmal gewartet, bis sich die Kugeln ausreichend still verhalten haben. Beobachtet hat er alles nur von außen und aus großer Entfernung. In der Kiste und in der Wand des Schuppens waren winzige Löcher und durch die hat Cavendish mit einem Teleskop sein Experiment kontrolliert. Der aus seiner Messung berechnete Wert der Gravitationskonstante betrug 6,74 mal 10 hoch minus 11 Kubikmeter pro Kilogramm pro Sekunde zum Quadrat. Das ist knapp ein Prozent Abweichung vom heute empfohlenen Wert. 1 Prozent Verbesserung in mehr als 200 Jahren! Wieso haben wir nicht mehr geschafft?
Das liegt nicht daran, dass wir es nicht probiert hätten. Natürlich gab es in der Zeit seit damals immer wieder neue Messungen. Am Messprinzip hat sich seit Cavendishs Zeit wenig geändert. Es geht immer noch darum, den Effekt zu messen, den zwei Massen aufeinander haben. Natürlich hat man die Methode schon ein wenig verbessert. Aber die Resultate blieben deprimierend ungenau. Verschiedene Experimente haben im Laufe der Zeit unterschiedliche Werte geliefert. Das ist eigentlich nicht ungewöhnlich in der Wissenschaft, aber man erwartet eigentlich, dass man sich immer genauer an den korrekten Wert herantastet. Bei der Gravitationskonstante kriegt man aber Werte, die nicht einmal innerhalb der Fehlergrenzen der Messung übereinstimmen. Man hat es mittlerweile dann auch mal mit komplett anderen Methoden probiert: Ohne zu sehr ins Detail zu gehen, geht es dabei darum, die Bewegung von Atomen in der Nähe einer mehr als 500 Kilogramm schweren Testmasse möglichst genau zu messen. Auch daraus kann man dann die Gravitationskonstante bestimmen und auch mit dieser komplett anderen Methode, die nichts mit den üblichen Gravitationswaagen zu tun hat, hat man Werte bekommen, die nicht mit den anderen übereinstimmen.
Womit wir jetzt beim vorhin erwähnten “andererseits” wären. Einerseits ist es deswegen so schwer, die Gravitationskonstante zu bestimmen, weil die Gravitation so eine enorm schwache Kraft ist. Andererseits klappt es aber vielleicht auch deswegen nicht, weil wir irgendwas grundlegendes noch nicht wirklich verstanden haben! Wir wissen ja, dass die Gravitation quasi das schwarze Schaf in der Physik ist. Die anderen Kräfte lassen sich alle “quantifizieren”, also in einer quantemechanische Beschreibung formulieren und in gewissen Ausmaß auch vereinheitlichen, also zusammenführen und als unterschiedliche Aspekte einer noch fundamentaleren Kraft beschreiben. Die Gravitation aber passt überhaupt nicht mit den restlichen Kräften zusammen. Einsteins Beschreibung der Gravitation als Krümmung der Raumzeit liefert zwar extrem genaue Vorhersagen die in den letzten 100 Jahren immer und immer wieder im Experiment und in Beobachtungen bestätigt worden sind. Ebenso wie die Aussagen der Quantenmechanik. Aber eigentlich sollte es möglich sein, beide Beschreibungen der Natur irgendwie zu kombinieren. Haben wir aber nicht hingekriegt, trotzdem wir es seit Jahrzehnten intensiv versuchen. Irgendwas haben wir bei der Gravitation also nicht nicht verstanden und damit natürlich auch bei der Gravitationskonstante. Vielleicht liegt es wirklich nur daran, dass wir sehr viel genauere Messungen brauchen. Vielleicht ist es aber auch grundlegender? Vielleicht ist die Gravitationskonstante gar nicht konstant? Es gibt ja immer wieder seriöse wissenschaftliche Hypothesen, die davon ausgehen, dass sich auch Natur”konstanten” im Laufe der Zeit ändern können. Entsprechende Beobachtungen von diversen Phänomenen im Universum wo das auffallen würde haben aber noch keine eindeutigen Hinweise geliefert. Wir können ja in der Astronomie auch in der Zeit zurück schauen; wenn wir zum Beispiel eine Supernova beobachten, deren Licht 10 Milliarden Jahre bis zu uns gebraucht hat, dann hat sie auch 10 Milliarden Jahre in der Vergangenheit stattgefunden. Wenn die Naturkonstanten damals anders waren, könnten wir das merken, wenn wir das Licht der Supernova analysieren. Haben wir bis jetzt aber nicht gemerkt… Aber vielleicht müssen wir auch hier noch genauer schauen.

Messungen der Gravitationskonstante im Laufe der Zeit (Bild: Dbachmann, CC-BY-SA 4.0)
Bis dahin wird uns nichts weiter übrig bleiben, als noch genauere Messungen anzustellen. 2021 hat man zum Beispiel die Gravitationskraft messen können, die zwischen zwei winzigen Kugeln wirkt, die nur wenig mehr als 90 Millimeter groß waren. Die Messung war noch viel ungenauer als die anderen; aber das war in dem Fall zu erwarten. Es ging hier vor allem darum zu zeigen, dass es überhaupt möglich ist, so eine enorm schwache Gravitationskraft _überhaupt_ messen zu können. In Zukunft geht das vielleicht genauer und wenn wir in der Lage sind, Gravitationskräfte auch auf so kleinen Skalen exakter zu messen, finden wir vielleicht auch einen Hinweis darauf, was das Problem an der Sache ist. Es ist auf jeden Fall kein akzeptabler Zustand, dass wir die Gravitationskonstante seit mehr als 200 Jahren nicht vernünftig messen können.












Kommentare (68)