 Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Wie man einen Planeten wiegt
von Daritz
Vor gut einem Jahr stellte ich mir die Frage, wie viel eigentlich die Sonnentrabanten wiegen und wie es möglich ist diese Massen zu bestimmen. Zu dieser Zeit war der Uranus nahe der Oppositionsstellung, also in einer Linie mit Erde und Sonne, darum entschied ich mich vorerst, mich auf den Gasriesen zu beschränken. Einen ersten Ansatz lieferte mir Archimedes: Nenn mir einen beliebigen Punkt und ich hebe die die Erde aus den Angeln!. Wieso also sollte dies mit dem Uranus nicht klappen? Durch das Hebelgesetz kann ich somit ganz einfach auf die Masse schließen! Leider hatte der Baumarkt nicht genug Holz für einen Hebel dieser Art. Ich musste mir also etwas anderes einfallen lassen…
Von Newton haben wir gelernt, dass die Bahn von Himmelskörpern um ein Gestirn, von der Masse ebendieses Zentralgestirns abhängt. Uranus hat einen ganzen Zoo von Monden, wenn man also die Bahnen dieser Monde misst, kann man auch auf die Masse des Uranus schließen. Um diesen Plan in die Tat umzusetzen waren zuerst Bilder nötig, Bilder die zeigen wie die Trabanten des Uranus diesen umkreisen. Zum Glück konnte ich als Teil der Astrogruppe meiner Schule, das schuleigene Teleskop für diese Beobachtung nutzen.
Natürlich wollte ich mir die Bewegung der Uranusmonde nicht durch visuelle Beobachtung merken, weshalb ich an 5 Nächten im Oktober Aufnahmen machte. Auf den mit sechs Sekunden belichteten Bildern sieht man Uranus und seine 4 größten Begleiter, Oberon, Titania, Umbriel und Ariel.
Aus diesen unscheinbaren Lichtpünktchen sollte ich nun etwas herauslesen. Um an die Quintessenz der Aufnahmen zu kommen, habe ich diese zuerst nach astronomischem Standard kalibriert. Dunkelbildabzug -klingt zwar kompliziert, ist es aber nicht- heißt die Methode um jegliches Licht, das nicht von den Sternen kommt, zu eliminieren. Dabei wird ein Bild mit geschlossenem Teleskopdeckel von den Lights, also den Aufnahmen des Planeten, abgezogen. Außerdem summierte ich die circa 20 Bilder jeweils einer Nacht um die gesamte Information nutzen zu können. Nun lagen mir fünf Bilder mit fünf unterschiedlichen Mondpositionen vor.
Mathe-du übernimmst!
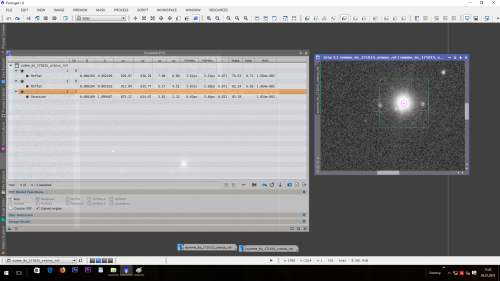
Da sich aus den fünf Bildern die Bahnen der Gesteinsbrocken die Uranus umkreisen nicht allein zeigen, musste ich ein wenig nachhelfen. Um die Bahnen herauszufiltern, las ich zuerst die relative Pixelpositionen der Monde, in Abhängigkeit von Uranus, ab. Die Astronomiesoftware PixInsight half mir dabei sehr. Ich habe nur Oberon und Titania verwendet, da die anderen beiden Monde zu nah am Planeten gelegen waren und so das Ablesen nicht optimal funktioniert hat.
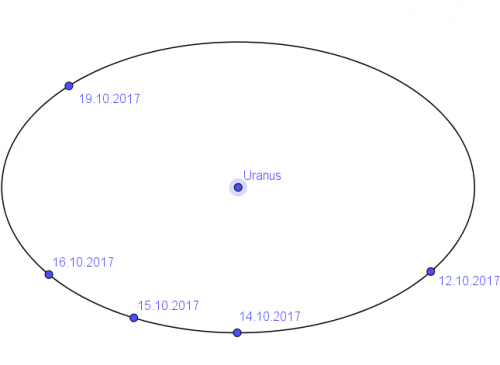
Diese Punkte trug ich nun in ein kartesisches Koordinatensystem ein. Durch die tolle Funktion der Geometrie Software GeoGebra gelang es mir eine Ellipse durch die fünf Punkte der fünf Nächte zu legen.
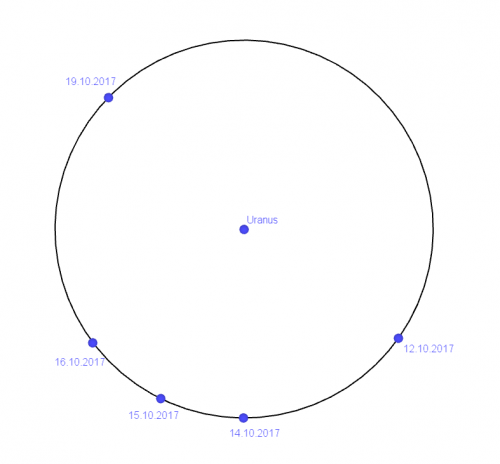
Eine wirklich stark exzentrische Ellipse. Sollte es sich nicht eigentlich um nahezu kreisförmige Bahnen handeln? Genau! Die Aufnahmen des Himmels sind zweidimensional, unser Universum ist jedoch dreidimensional, wir leben ja nicht im Flachland.:) Die Ellipse ist also nur eine Projektion der reellen Umlaufbahn, die nahezu kreisförmig ist. Jetzt gilt es, um die Bahnen richtig zu vermessen, die Ellipse zu deprojizieren! Dazu muss ich schwere Geschütze auffahren…Mathe! Mit ein wenig Vektorrechnung gelang die Deprojektion.
Fast Halbzeit! Die Umlaufzeit der Monde Oberon und Titania konnte ich ausrechnen, da ich wusste, wieviel Zeit zwischen 2 Beobachtungstagen vergangen ist.
Leider fehlt mir noch der Radius. Dieser liegt mir nur in Pixeln oder als Winkel unter dem diese Pixel erscheinen vor. Nicht erschrecken, den Winkel gibt mir die Kamera mit der die Aufnahmen gemacht worden sind, da diese nur einen gewissen Ausschnitt des Himmels abbildet. Um diesen Winkel in absolute Werte umzurechnen braucht man die Entfernung zum Gasriesen selbst.
Ein Planet im Rückwärtsgang
Um zu zeigen, wie ich den Radius der Mondbahnen ermittelt habe muss ich ein wenig ausholen. Die Bilder der fünf Nächte zeigen nicht nur die Bewegung der Uranustrabanten sondern auch eine Bewegung des Uranus selbst. Klar, der Planet bewegt sich ja um die Sonne….Falsch! Uranus bewegt sich so dermaßen langsam, dass es sich hier um die Erde handelt die am Uranus vorbeizieht. Der Gasriese bewegt sich also von der Erde aus gesehen rückwärts! Diese scheinbare Verschiebung wird auch Parallaxeneffekt genannt.
Damit konnte ich etwas anfangen! Wenn man nämlich weiß, wie stark dieser Parallaxeneffekt ist, kann man die Entfernung zum Objekt ermitteln. Mit dieser Entfernung war es mir nun möglich die Pixelwerte der Mondbahnradien in absolute Werte umzurechnen.
Endspurt!
Für eine kreisförmige Bewegung ist die sogenannte Zentripetalkraft nötig. Als Zentripetalkraft kommt bei Umlaufbahnen nur die Gravitationskraft infrage.

Veranschaulichung der Zentripetalkraft
Quelle:https://de.wikipedia.org/ Urheber: Tobias Rütten
Lizenz: https://creativecommons.org/licenses/by-sa/2.5/deed.de
Nun setzte ich also die Formeln der beiden Kräfte gleich, setzte die ermittelten Bahndaten in die Formel ein und formte auf die Masse des Zentralkörpers um! Et voilá:
Ich habe nun einen Gasriesen ohne eine herkömmliche Haushaltswaage gewogen! Wenn ihr das nächste mal eine Planetenmasse bei Wikipedia nachschlagen wollt, überlegt zweimal ob ihr sie nicht lieber selbst ermittelt.;)


















Kommentare (22)