Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Das Hobby englischer Ladies und andere mathematische Rätsel
von Hrvoljub Vukman
Es geht um hauptsächlich um das Ladies’ Diary, welches im 18. Jahrhundert veröffentlicht wurde, und zur Zerstreuung englischer Damen diente. Es wurden aber auch relevante mathematische Fragestellungen behandelt. Diese führten zu den modernen Fachmagazinen. Dies stelle ich an Hand eines relativ einfachen Problems dar. Um dies zu verstehen, muss man nur wissen was ein Bruch und was eine Primzahl ist.
The Ladies‘ Diary erschien jährlich von 1704 bis 1841. Es war ein kleines Magazin, etwa 10 cm weit und 16 cm hoch. Bis 1744 war es etwa 40 Seiten lang. Zuerst kostete es 3 Pence, um die Hälfte teurer als andere vergleichbare Magazine. Jede Ausgabe hat das Porträt einer bekannten englischen Frau auf dem Frontcover. Oft waren die Untertitel sehr spezifisch, wie im Jahr 1836:
The Ladies Diary, For the Year of Our Lord 1835, Being the Third After Bissextile. Designed specifically For the Amusement and Entertainment of The Fair Sex With An Appendix of Curious and Valuable Mathematical Papers For the Use of Students. The Hundred and Thirty Second Almanack Published of this Kind. Also The Gentleman’s Diary Or, The Mathematical Repository; An Almanack For the Year of Our Lord 1835 and 1836 Being The Third or Bissextile or Leap Year Containing many Useful and entertaining Particulars peculiarly adapted to the Ingenious Gentleman engaged in the delightful Study and Practice of the Mathematicks.
Ladies and Gentlemans Diary des Jahres 1777 (Bild: Public Domain)
Dies war eines der zahlreichen Almanache, die auf dem Markt erschienen. Diese Jahrbücher deckten oft einen sehr eingegrenzten Bereich eines Fachgebietes ab, wie zum Beispiel das Nautical Almanac, welches sich auf die Navigation auf der See beschränkte Link zum Wikpedia Eintrag des Nautischen Almanachs
Das Ladies Diary war ein englischer Almanach, dass sich hauptsächlich an Frauen richtete oder an das „Fair Sex“. Diese gab es auch in Deutschland, wie das Frauenzimmeralmanach, das von 1784 bis 1820 in Leipzig erschien, das hauptsächlich Gedichte, Texte und Lieder enthielt. Zum Beispiel im Jahr 1807 eine Szene aus der Familie Ehrenberg, wohl möglich ein Fortsetzungsroman:
Fast in Gram versunken saß Charlotte da und Thränen standen in ihren Augen, als ihr Gatte zu ihr ins Zimmer trat.
Frauenzimmeralmanach aus dem Jahr 1817 (Andreas Praefcke, gemeinfrei)
Das Diary wurde 1704 John Tipper (1680-1713) erstmals veröffentlicht. Es richtete sich hauptsächlich an Frauen. Ein Zitat was von ihm überliefert ist, zeigt seine Einstellung:
I cannot but take notice of the Hardship the fair Virgin is reduced to, in that she may not court the Man she loves, but only accept in Marriage one of those who happen to court her, whereas the Men may address themselves to whom they please; this, I must confess is very unequal…” Quelle (Seite 13)
Im Ladies Diary gab es Tabellen von Sonnenauf- und untergängen, eine Chronik von Ereignissen des vergangenen Jahres und auch zahlreiche Rätsel, Enigmas genannt. Diese wurden üblicherweise im nächsten Jahr im neuen Band aufgelöst. Rätsel waren erst nur in Reimform gegeben, wie dieses:
If to my Age there added be
One Half, one Third, and three times Three;
Six score and ten the Sum you’ll see,
Pray find out what my Age may be?
Die Diaries sind auf Grund ihres Alters, frei im Internet verfügbar. Hier ist eins aus dem Jahr 1787
In ihm wurden auch mathematische Probleme der Zeit behandelt. Ähnliche Magazine gab es in Deutschland, unter anderem das Acta eruditorum (gegründet in 1682 Leipzig) Zahlreiche mathematische Probleme wurden in diesem Magazin behandelt. Darunter war das bekannteste das Problem der Brachistochrone , oder die Kurve kürzester Fallzeit in 1696.
Das Ladies Diary wurde insgesamt 137 Jahre veröffentlicht. Um diese Zeit gab es nur kaum wissenschaftliche Magazine. 1700 gab es in England nur das „Philosophical Transactions of the Royal Society”. Der wissenschaftliche Austausch beschränkte sich zu der Zeit hauptsächlich auf Almanache.
Das Magazin war an Frauen gerichtet, die Fragesteller waren aber meistens Männer. 17 Beiträge von 1748 bis 1768 kamen von Frauen. Aber es wurden oft Pseudonyme verwendet. Es könnten demnach mehr Frauen beteiligt sein, diese blieben aber anonym. Um darzustellen wie mathematische Probleme in der Mitte des 18. Jahrhunderts aussahen, möchte ich eine Frage aus dem Jahr 1747 behandeln:
It is required to find (by a general theorem) the number of fractions of different values, each less than unity, so that the greatest denominator be less than 100?
Übersetzung: Wie viele eindeutige Brüche gibt es die: a) kleiner als eins sind und b) einen Nenner haben der kleiner als 100 ist. Die Null wird ausgeschlossen
Hier ist eine Aufzählung von Brüchen die kleiner als eins sind. 1/2, 1/3, 2/3, 1/4,…. Somit ist 99/100 der letzte Bruch in dieser Aufzählung.
Was heißt eindeutig? Beispiel: 1/2 und 2/4 sind beide gleich. Ebenfalls 1/3 und 3/9 usw. Ein Bruch der eindeutig ist, ist 5/7.
Hier sieht man schon das Primzahlen wichtig werden.
Wir betrachten erst einmal die kleineren Zahlen. Wir fangen bei der zwei an. Da gibt es nur einen Bruch, der alle Anforderungen erfüllt: 1/2.
Bei der drei: 1/3 und 2/3.
Bei der vier: 1/4, 3/4. 2/4 ist gleich 1/2 und demnach nicht mitgezählt.
Bei der fünf: 1/5, 2/5, 3/5, 4/5.
Bei der sechs: 1/6, 5/6.
Vielleicht sieht man bei der sechs, dass die 2/6, 3/6 und 4/6 nicht darunter sein können, weil diese Zahlen mit der sechs nicht teilerfremd sind oder wie in der Schule gesagt: man kann diese Brüche nicht kürzen. Diese Zahlen sind damit relativ prim zueinander. Wikipedia-Eintrag zur Teilerfremdheit
Dies kann man auch feststellen über die Primfaktorzerlegung.
12 und 77 sind relativ prim, weil die eindeutige (!) Zerlegung der Zahlen in Primzahlen (12= 2*2*3 und 77=7*11) keine gemeinsamen Faktoren besitzen. 15 und 25 sind nicht relativ prim, da 15=5*3 und 25=5*5 ist. Die fünf ist demnach der größte gemeinsame Teiler. Deswegen ist auch die Eins keine Primzahl, weil sonst die Zerlegung einer beliebigen
natürlichen Zahl in Primzahlen nicht eindeutig wäre. Zum Beispiel: 15=5*3*1=5*3*1*1 usw. Die Lösung des Rätsels wäre demnach für alle Zahlen von 1 bis 99 eine Methode zu finden, die Anzahl der jeweiligen relativen Primzahlen zu finden.
Gibt es so eine Funktion? War sie schon 1747 so bekannt? Ja, es gibt so eine Funktion. Sie wurde aber erst 1763 von Euler so definiert. Die Funktion die teilerfremden Zahlen findet heißt Eulersche Phi Funktion . Es sei aber gesagt, dass diese nur die Anzahl der teilerfremden Zahlen gibt, nicht wie diese Zahlen aussehen. Es ist aber auch nicht danach gefragt worden.
Die Aufgabe wurde erst vier Jahre (1751) später, von einem Herrn Flitfick, gelöst. Hier muss auch anmerken, dass dieses Almanach nicht nur von Amateuren oder auch Frauen gelesen wurde. Vor der Zeit der mathematischen Fachjournale und der Erfindung des Berufes des Mathematikers, wurden diese Magazine der Weg zum wissenschaftlichen Austausch. Man findet auch weitaus schwierigere Probleme beim Durchlesen anderer Ausgaben.
Die Phi Funktion, hier f genannt, hat auch weitere nützliche Eigenschaften:
Diese Funktion ist multiplikativ. Heißt: 
Zum Beispiel: 
Die Vielfachen von 2 die kleiner oder gleich 16 sind, sind: 1*2=2, 2*2=4, 3*2= 6, 4*2=8, 5*2=10, 6*2=12, 7*2=14 und 8*2=16. Die Zahlen, die nicht aufgelistet sind und kleiner als 16 sind: 1, 3, 5, 7, 9, 11, 13, 15. Diese sind demnach relativ prim zu 16. Davon gibt es insgesamt acht. Wenn man dann nachrechnet, erhält man in der Tat: f(2^4) = 2^4 – 2^3 = 16 – 8 = 8.
Um die Aufgabe zu lösen muss man die Phi-Funktion für jede Zahl von zwei bis 99 zu berechnen und dann einfach addieren. Dabei helfen die beiden vorher gezeigten Eigenschaften der phi-Funktion, um die Rechenzeit zu verkürzen. So ähnlich wurde diese Aufgabe auch vier Jahre später (1751) von einem Herren Flitcon gelöst. Er stellte höchstwahrscheinlich
eine Tabelle der richtigen Zahlen auf. Die richtige Lösung ist 3003. Es ist nicht klar wie genau diese Frage nach Frankreich gelang. Eine Sammlung der mathematischen Fragen des Diary von 1704 bis 1760 war aber später im Umlauf.
Diese Sequenz von teilerfremden Brüchen ist auch als Farey Folge bekannt. Formal ist eine Farey Folge eine Ordnung von Brüchen, die immer größer werden und aus teilerfremden Brüchen besteht.
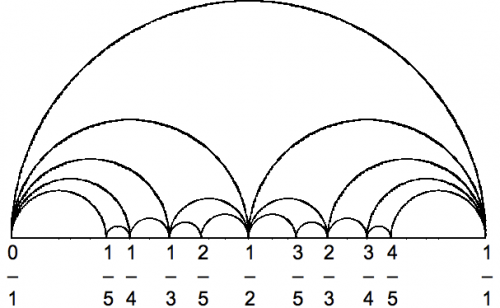
Farey Folge für die Zahl 5 (Bild: Hyacinth, public domain)
Die Farey Folge von 5, F(5) ist: 0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1, da hier der Nenner maximal fünf ist und alle Brüche eindeutig und kleiner als null ist.
Die Lösung der Aufgabe nach Anzahl der Brüche die kleiner als eins ist, ist gleichwertig mit der Frage:
Was ist die Länge der Farey Folge der Ordnung 99 (minus des ersten und letzten Eintrags)?
Diese und ähnliche Folgen wurden in Magazinen im 19. Jahrhundert besprochen. Frankreich war zu der Zeit führend in der mathematischen Forschung. Die Tabelle der Farey Folgen wurde 1806 im „Journal de l‘Ecole Polytechnique“ veröffentlicht, dem Magazin der Polytechnischen Schule in Paris. Dieses war schon professioneller als das Ladies‘ Diary und richtete sich explizit an Wissenschaftler an Universitäten. Die Tabelle wurde im Artikel: Tables pour évaluer une fraction ordinaire avec autant de decimals qu’on voudra; et pour trouver la fraction ordinaire la plus simple, et qui approche sensiblement d’une fraction décimale im Jahr 1801 in diesem Magazin veröffentlicht.
Von hier ging die Farey Folge wieder nach Großbritannien und einem Pensionär namens Henry Goodwyn.
Er erstellte ebenfalls eine solche Tabelle von eindeutigen Brüchen. Goodwyn erstellte eine Tabelle mit Nennern von 1 bis 1024. Einen Monat nach dem Goodwyn diese der Royal Society vorgestellt hat, veröffentlichte der Geologe John Farey in The Philosophical Magazineand Journal einen Brief mit dem Namen: „On a curious Property of the vulgar Fractions”. Hier stellte er die Frage bezüglich der Tabelle:
I am not acquainted, whether this curious property of vulgar fractions has been before pointed out?; or whether it may admit of any easy or
general demonstration ?; which are points on which I should be glad to learn the sentiments of some of your mathematical readers; …”
Dies bezieht sich auf die folgende Eigenschaft der Folge. Wenn a/b und c/d beide kleiner als null sind, und ad – bc kleiner als 1 ist, dann gilt:
Wenn a/b und b/c Nachbarn sind, dann taucht (a+c)/(b+d) zwischen ihnen in der Folge F(b+d) auf.
Ein Beispiel: Wir nehmen 1/3 und 2/5 (a=1, b=3, c=2, d=5). Diese sind in der oben genannten Folge F(5) Nachbarn. Hier ist a+c=3 und b+d=8. In der Folge F(8) ist (a+c)/(b+d)= 3/8 zwischen den Werten 1/3 und 2/5.
Diese Eigenschaft wurde von Farey nur vorgeschlagen und nicht bewiesen. Diese Frage reiste dann von England wieder nach Frankreich. Dort bewies Augustin-Louis Cauchy diese Eigenschaft im Jahr 1816. So erhielt diese Folge auch ihren Namen, Faurey Folge, obwohl er nicht den Beweis geliefert hat. Diese Geschichte zeigt wie sich eine Forschungsfrage im 18. und 19. Jahrhundert verbreitete und wie solche und ähnliche Folgen und Gleichungen ihre Namen erhalten.
1841 war Schluss mit der Publikation des Diary. Es wurde von wissenschaftlichen Magazinen abgelöst. Am Ende des Magazins wurden mit Aufkommen der Leibniz Notation die Fragen deutlich schwerer und richteten sich an ein männliches Fachpublikum, da Frauen der Zugang zu Universitäten in England verwehrt blieb. Zum Beispiel in 1838:
Question 1637 by Mr. John Cam, Torpenham, Cumberland
Required the curve in which the integral 
Diese Frage ist für einen Hobbymathematiker, oder eine Frau ohne höhere Mathematikkenntnisse, nicht zu beantworten. So hat sich der Zweck dieses Magazins überlebt. Es hatte aber großen Einfluss auf eine Generation kommender Mathematiker. Laut einer anonymen Umfrage im Philosophers Magazine im Jahr 1819 wurde das Ladies Diary als eines der wichtigsten Magazine genannt.
Erst später konnten Frauen am akademischen Leben teilhaben. Der offizielle Zugang für Frauen an Universitäten kam 1869 mit den London Nine. 1880 erhielt die erste Frau ,Charlotte Scott , einen Bachelorabschluss in Mathematik an der Cambridge University.
Kommentare (5)