Von großen und kleinen Tieren

Jeder hat das sicher schon einmal gelesen: “Wenn ein Floh so groß wäre wie ein Mensch, könnte er über ein Hochhaus springen.” “Wenn eine Ameise so groß wäre wie ein Mensch, könnte sie ein Auto tragen.” So anschaulich und beeindruckend das klingt, es ist leider falsch. Um zu verstehen, warum das falsch ist, müssen wir eine Brücke von der Biologie zur Mathematik schlagen.

Ein kleines Experiment

Wir beginnen mit einem einfachen Experiment. Dazu nehmen wir neun Würfel (für die Rollenspieler unter euch: sechsseitige Würfel). Acht davon stapeln wir so aufeinander, dass sich ein größerer Würfel ergibt:

Offensichtlich hat der große Würfel die doppelte Kantenlänge des kleinen Würfels. Wie steht es mit seiner Oberfläche? Der kleine Würfel hat sechs Seiten, beim großen Würfel haben wir auf jeder der sechs Seiten vier Würfelflächen der kleinen Seiten, macht also 24. Die Oberfläche ist also um das Vierfache gestiegen.

Und das Volumen? Das ist einfach – da wir acht Würfel brauchten, ist es offensichtlich achtmal so groß. Wenn wir den Würfel in der Länge verdoppeln, vervierfacht sich also seine Oberfläche, sein Volumen verachtfacht sich.

Allgemeiner gilt: Vergößere ich ein Objekt in der Länge (in jeder Richtung) um einen Faktor L, dann vergrößert sich seine Oberfläche um den Faktor L*L (also L²), sein Volumen sogar um L*L*L (also L³). Regeln dieser Art, die angeben, wie sich eine Größe ändert, wenn man ein Objekt vergrößert oder verkleinert, nennt man Skalierungsgesetze. Die Biologie ist voll davon – einen guten Einblick gibt das Buch von Schmidt-Nielsen (s. Quellen).

Warum Elefanten große Ohren haben

Diese einfache Beziehung ist der Grund dafür, warum Elefanten (afrikanische jedenfalls) große Ohren haben. Wieso das? Elefanten sind “Warmblüter”², produzieren also sehr viel Körperwärme. Diese muss im heißen afrikanischen Klima abgeführt werden, das geht natürlich nur durch die Körperoberfläche.

²Für alle spitzfindigen Biologen: Ich weiß, “Warmblüter” ist kein so gern gesehener Begriff. Ich hätte auch homöotherme tachymetabolische Endotherme statt “Warmblüter” schreiben können…

Betrachten wir einen Elefanten und einen auf die Hälfte verkleinerten Elefanten. Der kleinere Elefant hat ein Achtel des Körpervolumens, produziert also auch nur ein Achtel der Körperwärme¹. Seine Körperoberfläche reduziert sich aber nur auf ein Viertel. Relativ zu seinem Volumen hat er also eine doppelt so große Oberfläche und kann deshalb Wärme viel besser abgeben. Mathematisch sieht man, dass das Verhältnis von Oberfläche zu Volumen sich wie 1/L verhält, je größer also ein Objekt, desto kleiner ist die relative Oberfläche.

¹Das ist für reale Tiere nicht richtig: Größere Tiere haben pro Kilogramm eine geringere Stoffwechselrate. Das genau zu verstehen ist eins der großen Rätsel der Biologie, darüber schreibe ich demnächst sicher auch mal etwas.

Elefanten, die ja sehr groß sind, haben also relativ gesehen eine kleine Oberfläche und können Wärme deshalb schlecht abstrahlen. Um überschüssige Wärme loszuwerden, sind deshalb große Ohren praktisch. (Wie meist in der Natur haben die Ohren natürlich zusätzlich noch andere Funktionen: beispielsweise als Signal zum Drohen.) Elefanten, die in kühlerem Klima leben oder mehr Wasser zur Verfügung haben (wie indische Elefanten), haben deshalb kleinere Ohren, die Ohren von Mammuts (die sich ja warm halten mussten) waren sehr klein. Auch Wüstenfüchse haben sehr große Ohren, ebenfalls als Wärmestrahler (gut hören können sie damit natürlich auch). Dass bei warmblütigen Tieren, die in kalten Regionen leben, die Extremitäten typischerweise kleiner sind, bezeichnet man als Allensche Regel.

Apropos Mammuts: Generell ist es so, dass Tiere, die in kaltem Klima leben, größer sind, weil sie dann weniger Wärme durch ihre Oberfläche verlieren. (Das ist die Bergmannsche Regel.)

Warum Elefanten eigentlich dünne Knochen haben
Vergleicht man die Skelette von kleinen und großen Tieren, so haben die großen offensichtlich dickere Knochen. Hier als Beispiel eine Katze (Univ. Washington) und ein Elefant (von Wikipedia), animiert mit gifsicle:

Elephantenbild von Sklmsta – Own work, CC0, Link

Tatsächlich sind die Knochen von Elefanten aber nicht ungewöhnlich dick, sondern (im Vergleich zur Katze) überraschend dünn. Um das zu verstehen, brauchen wir wieder unsere Skalierungsgesetze. Ein Elefant wiegt grob geschätzt tausendmal mehr als eine Katze (so 6kg ist ein guter Schätzwert für einen Stubentiger, 6t passt für einen afrikanischen Elefantenbullen). Damit müsste der Elefant etwa zehnmal größer sein (denn skaliere ich die Länge um den Faktor 10, vergrößert sich das Volumen und damit die Masse um den Faktor 1000). Die Schulterhöhe eines Elefantenbullen liegt so zwischen 3 und 4 Metern, dann müsste die Katze so etwa 30 bis 40cm Schulterhöhe haben – ich habe gerade keine Katze griffbereit, aber so ungefähr sollte das stimmen. (Kurzer Check im Internet: Hier gibt es als Beispiel die Maine-Coone-Katze mit Schulterhöhe 40cm und Masse von 5-9kg. Passt also.)

Diese Masse muss das Tier aber auch mit sich herumtragen können. Die Tragfähigkeit von Knochen (oder überhaupt von jeder Art von tragender Struktur) ist proportional zur Querschnittsfläche. Wenn man die Katze auf Elefantengröße skaliert, dann nimmt ihre Masse um das Tausendfache zu, der Querschnitt der Knochen nur um das Hundertfache. Die Knochen würden also zehnmal stärker belastet, Knochenbrüche wären vorprogrammiert.

Um das zu vermeiden, müssen die Knochen von Elefanten also dicker sein. Wieviel dicker? Die Fläche muss sich im Vergleich zur Länge verzehnfachen, also müsste sich der Durchmesser etwa verdreifachen (3 mal 3 ist neun und der Rest ist beim Abschätzen unwichtig). Hier mal die Oberschenkelknochen von Katze (links) und Elefant (mitte) aus den Fotos herauskopiert, gedreht und auf die gleiche Länge gebracht. Rechts daneben habe ich eingezeichnet, wie dick der Elefantenknochen sein müsste, um die “richtige” Querschnittsfläche zu haben:

Elephantenbild von Sklmsta – Own work, CC0, Link

Ganz so dick ist der echte Elefantenknochen dann doch nicht – Elefanten haben also eigentlich dünnere Knochen, als man erwarten könnte. Dass die Knochen großer Tiere im Verhältnis dicker sein müssten, wusste übrigens schon Galilei (hier ein Bild aus den “Discorsi”):

Wie schaffen es Elefanten aber, dass ihre Knochen nicht brechen? Ganz einfach – habt ihr schon mal einen Elefanten gesehen, der auf einen Schrank springt? Eben. Elefanten sind ja eher behäbig (obwohl sie ziemlich schnell laufen können) und setzen ihre Beine immer schön gerade und senkrecht auf. Dadurch vermeiden sie große Biegekräfte, die bei Tieren wie Katzen (und auch uns Menschen) die größte Knochenbelastung ausmachen.

Wenn ihr mal die Gelegenheit habt, ein Elefantenskelett aus der Nähe zu betrachten, dann könnt ihr übrigens sehen, dass der Oberschenkelknochen im Querschnitt nicht einigermaßen rund ist wie bei der Katze (oder bei uns), sondern dass er fast plattenförmig ist – in vorwärts-rückwärts-Richtung ist er vergleichsweise dünn (wie oben auf den Bildern), aber wenn man von vorn drauf schaut sieht man, dass er sehr breit ist. Das ist gut verständlich, denn wenn der Elefant ein Bein anhebt, wirken auf das Bein, das noch am Boden ist, natürlich Biegekräfte in dieser Richtung. Eine schöne Fotostrecke mit einem Elefantenskelett habe ich übrigens gerade hier auf der Seite des Liverpool-Museums gefunden.

Bei den großen Dinosaurier, den Sauropoden, ist das übrigens ganz ähnlich, auch da sind die Beinknochen viel breiter als dick.

Trotzdem sind natürlich die Knochen des Elefanten im Verhältnis zu Katze dicker. Was genau diese Dicke bestimmt, dazu gibt es verschiedene Theorien, die ich jetzt hier nicht alle ausbreiten will. Wer mehr wissen will, kann unten bei Schmidt-Nielsen nachgucken (oder ihr nörgelt in den Kommentaren rum, dass ich dazu auch mal was schreiben soll…).

Und das erklärt jetzt auch, wie das mit der Ameise ist. Ameisen haben verdammt dünne Beine (mit einem Außenskelett), trotzdem können sie das Vielfache ihres Körpergewichts tragen. Tja, wenn ich so klein wäre, könnte ich das auch. Würde ich mich um den Faktor 100 in der Länge verkleinern, dann würde mein Körpergewicht um den Faktor eine Million abnehmen, meine Kraft aber nur um den Faktor Zehntausend. Ich könnte also locker das Hundertfache meines Körpergewichts tragen. (Allerdings hätte ich ne Menge andere Probleme, unter anderem mit dem Wärmehaushalt, weil ich so viel Wärme abstrahlen würde.) Ameisen haben also keine besonders leistungsfähigen Muskeln oder Ähnliches, sie sind einfach nur klein. Genial gute Animationen zu diesem Thema gibt es auf der Seite Understanding Evolution der Uni Berkeley (unbedingt anklicken!)

Wer springt am höchsten?

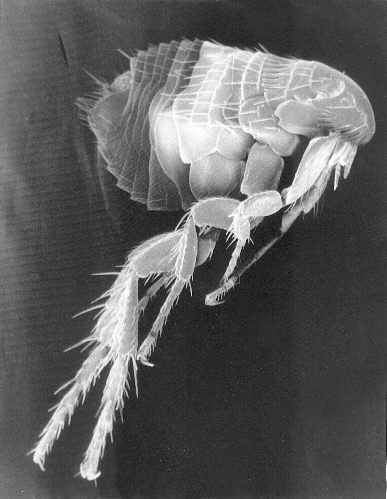
By Content Provider(s): Centers for Disease Control and Prevention (CDC) / Janice Carr – https://phil.cdc.gov/PHIL_Images/05072002/00001/PHIL_240_lores.jpg, Public Domain, Link

Und wie war das mit dem Floh? Wodurch wird überhaupt bestimmt, wie hoch ein Tier springen kann?

Dazu brauchen wir ein bisschen Physik – aber keine Sorge, sehr kompliziert wird’s nicht.

Beim Hochspringen müssen wir ja gegen die Schwerkraft anarbeiten. Dazu müssen wir Energie aufwenden. Die benötigte Energie E, um ein Objekt der Masse m auf eine Höhe h zu bringen, ist
E=m g h
dabei ist g die Erdbeschleunigung (so etwa 10m/s²).

Die Höhe ist also h=E/ (mg), wenn man die Energie kennt.

Woher kommt die Energie? Die kommt vom Abspringen, dabei werden wir beschleunigt. Das erledigen die Muskeln. Nehmen wir ganz vereinfacht an, die Muskeln würden die ganze Zeit mit konstanter Kraft F arbeiten, bis die Füße den Boden verlassen. Arbeit ist Kraft mal Weg, also E=F s, wenn s der Beschleunigungsweg ist. Der Beschleunigungsweg ist durch die Beinlänge gegeben, je länger er ist, desto höher die Endenergie. (Deshalb geht man auch in die Knie, wenn man aus dem Stand hochspringt.)

Der Beschleunigungsweg verhält sich also wie die Beinlänge, skaliere ich das Bein auf die doppelte Länge, dann wird auch der Weg doppelt so groß (wenn alles andere gleich bleibt). Ich schreibe kurz s~L, wobei die Tilde für “proportional zu” steht, und das L die Länge des Tiers ist.

Die Muskelkraft F ist, genau wie die Festigkeit eines Knochens, bestimmt durch die Querschnittsfläche. Die verhält sich wie L², also F~L².

Sammeln wir die beiden Abhängigkeiten auf und setzen sie bei E=Fs ein, dann ergibt sich
E~L³
In der Formel für die Sprunghöhe stand noch die Masse, die ist natürlich auch proportional zu L³. Insgesamt ergibt sich also
h=E/mg ~ L³/L³ = konstant.
Die Sprunghöhe von Tieren ist nach dieser Rechnung also von der Größe des Tieres unabhängig.

Das klingt auf den ersten Blick absurd, ist aber gar nicht so unsinnig. Kängurus springen so etwa drei Meter hoch, aber auch Buschbabies (kleine Lemuren) können aus dem Stand auf einen Türsims springen, schaffen also auch etwa zwei Meter Höhe, obwohl sie wesentlich kleiner sind. Ein Floh springt etwa 20cm hoch, eine 1000 mal schwerere Heuschrecke etwa 60cm, ein durchschnittlicher Mensch schafft vielleicht 70 Zentimeter (die Sprunglatte liegt zwar höher, aber der Mensch beginnt ja auch schon mit einem Schwerpunkt, der etwa in Bauchnabelhöhe sitzt).

Aber kleine Tiere, beispielsweise Ameisen, springen ja normalerweise nicht besonders hoch, und der Floh ist doch gerade deshalb als Springer so berühmt, weil die meisten Tiere seiner Größe eben nicht so hoch springen können. Irgendwas fehlt also in der Rechnung.

Was fehlt ist die benötigte Beschleunigung. Wenn die Beschleunigungsstrecke s sehr kurz ist, dann muss die notwendige Kraft sehr schnell aufgebracht werden. Und da gibt es ein Problem, denn Muskeln werden um so schwächer, je schneller sie sich kontrahieren. Ein Floh braucht eine Beschleunigung, die die 245-fache Erdbeschleunigung beträgt, um sich in die Höhe zu schnellen, weil seine Beine so kurz sind – so schnell kann kein Muskel kraftvoll kontrahieren.

Der Floh verwendet deshalb einen Trick: Er spannt seine Muskeln langsam an, speichert die Energie aber zunächst in einem Block aus einem biologischen Gummi, das zunächst arretiert ist. Zum Abspringen wird die Arretierung gelöst, das Gummi dehnt sich blitzartig aus (jaja, die Macht der Entropie) und der Floh wird in die Höhe katapultiert.

Wäre der Floh so groß wie ein Mensch, bräuchte er diesen Mechanismus aber nicht. Trotzdem könnte er (entsprechend skaliert) wegen seiner langen Hinterbeine vermutlich etwas besser springen als ein Durchschnittstier, aber Hochhäuser schafft nur Supermann…

Die absolute Bibel zum Thema Skalierung in der Biologie (wenn auch stellenweise nicht mehr aktuell) ist
Knut Schmidt-Nielsen, Scaling: Why is Animal Size so Important?

Sehr gut zu lesen ist auch
Chris Lavers, Why elephants have big ears
da geht es zu einem guten Teil um Warm- und Kaltblütigkeit und welche Vorteile sie bieten, aber auch um Artenvielfalt und viele andere Themen.

Die Überlegungen zur Sprunghöhe stammen im wesentlichen aus
Steve Vogel, Life’s Devices
einem Buch, das ich auch sehr empfehlen kann.