Dass jemand, der über numerische Verfahren in der Elementarteilchen promoviert hat und an einem Maschinenbauinstitut Werkstoffe simuliert, Koautor einer Veröffentlichung über Dinos wird, ist vermutlich schon eher ungewöhnlich. Wie ich dazu kam, mich fachlich mit Dinosauriern zu beschäftigen, wie so eine Forschungskollaboration funktioniert und worum genau es ging, das will ich in diesem dritten Teil der Serie erzählen. (Und im vierten Teil schauen wir dann hoffentlich endlich in die Veröffentlichung selbst – aber wie ihr sehen werdet, waren die Wege dorthin ziemlich verschlungen.) Und wer fleißig liest, bekommt zur Belohnung nicht nur ein interaktives Java-Applet zum Rumspielen, sondern kann auch bisher unveröffentlichte Forschungsergebnisse studieren.
Weil es sich hier um meine ganz persönliche Forschung handelt, fange ich mal ganz am Anfang an.
Seit ich (ich glaube, am Anfang der 4. Klasse) den Film “Reise in die Urwelt” gesehen hatte, war ich von Dinosauriern und vorzeitlichen Tieren fasziniert. Paläontologe wollte ich trotzdem nicht werden. Dinos hätte ich schon gern erforscht, aber das in den Dino-Büchern viel geschilderte abenteuerliche Ausgraben von Knochen in irgendeiner Wildnis fand ich wenig attraktiv – auch die Geduldsarbeit des Herauspräparierens von Knochen aus dem umgebenden Gestein war nichts für mich, das war mir auch als Kind klar. Wenn man Dinosaurier auch ohne das hätte erforschen können, das wäre vielleicht schon etwas gewesen, aber so…?
Später verlagerte sich mein Interesse ohnehin mehr in Richtung Physik. Dinosaurier fand ich immer noch faszinierend (besonders das Buch “Die Welt der Dinosaurier” von LSB Halstead, in dem viele biomechanische Gesichtspunte – wenn auch aus heutiger Sicht fehlerhaft – diskutiert wurden, fand ich spannend), aber zum Beruf wollte ich sie nicht machen. Und irgendwann nahm das Interesse auch ab, denn gerade in den 80ern war Deutschland in Sachen Dinosaurier in gewisser Weise ein Entwicklungsland – Fernsehsendungen gab es vielleicht einmal im Jahr, in den verfügbaren Büchern stand immer mehr oder weniger dasselbe, viel Neues schien es nicht zu geben.
Erst Mitte der Neunziger änderte sich das – dank des damals noch neuen Internets fand ich (ich glaube auf Tipp eines Kollegen) die “Dinosaur mailing list” – die Dinosaurierforschung war alles andere als tot, sie war lebendig wie nie. Nach einer Weile wurde mir klar, dass ich Dinosaurierbücher auf Englisch lesen konnte – und dann begriff ich, dass ich mit etwas Mühe womöglich sogar die Fachliteratur würde verstehen können, wenn ich mir den entsprechenden Jargon aneignete.
In den Jahren danach las und diskutierte ich fleißig auf der mailing-liste, las (na klar, in meiner Freizeit – dass ich jemals echte Forschung auf dem Gebiet treiben würde, ließ ich mir immer noch nicht träumen) Bücher und Arbeiten und lernte Anatomie und Biomechanik, bis ich das rostrale vom caudalen Ende eines Dinosauriers unterscheiden konnte und wusste, wo Surangular und Postorbital zu finden sind. (Ich fühlte mich des öfteren an die Geschichte von Feynman erinnert, als er für einen Vortrag bei den Biologen eine “map of a cat” suchte – so etwas hätte ich damals auch gut gebrauchen können; irgendwann habe ich mir dann selbst eine gemacht – also nicht für eine Katze, sondern für einen Dino.)
Am spannendsten fand ich immer die Biomechanik – da wo Physik und Evolution ineinandergreifen, um Lebewesen zu formen. Und so habe ich natürlich auch das Nature-paper von John Hutchinson, von dem ich beim letzten Mal erzählt habe, gelesen. Irgendwann im Januar oder Februar 2005 las ich dann (auf der Mailing-Liste der Society for Vertebrate Paleontology), dass John Hutchinson einen Doktoranden für Finite-Element-Simulationen in der Biomechanik suchte. (Finite-Element- oder kurz FE-Simulationen sind das Standardwerkzeug der Ingenieure, wenn es um die Berechnung von Belastungen und Verformungen geht und sozusagen mein tägliches Brot. Sollte ich auch mal irgendwann erklären (auf die Liste eintrag…))
Gut, einen Doktor wollte ich nicht noch einmal machen – aber wenn jemand einen Doktoranden für FE-sucht, in seinem Labor auf diesem Gebiet aber noch nicht viel geforscht wird, dann, so schloss ich messerscharf, hat er ja vielleicht Interesse, mit jemandem zusammenzuarbeiten, der sich auf diesem Gebiet auskennt. Also schrieb ich ihm eine mail. Eine halbe Stunde später hatte ich schon eine freundliche Antwort, und nach nicht mal einer Woche hatten wir einen Besuchstermin vereinbart. (Dazu musste ich noch bei meinem Chef ein paar Reisemittel loseisen – er fand die Idee, Dinos zu simulieren, zwar wohl etwas abstrus, spendierte das Geld aber trotzdem.)
Im April war ich dann am Royal Veterinary College vor den Toren von London. In den knapp zwei Tagen, die ich da war, redeten wir über diverse Möglichkeiten zur FE-Simulation und ich sprach auch mit vielen von Johns Kollegen über Zusammenarbeitsmöglichkeiten – aus keiner dieser Ideen wurde allerdings bisher etwas. Doch kurz bevor ich abreiste (ich hatte nur noch ein paar Minuten Zeit) fragte John mich quasi aus heiterem Himmel, ob ich mich mit Optimierungsproblemen auskennen würde. Ohne unbescheiden sein zu wollen – das ist näherungsweise so, als ob man Graeme Dott fragt, ob er schon mal Billard gespielt hat – Optimierungsprobleme waren ein Kernbestandteil meiner Dissertation und etwas, woran ich immer viel Spaß hatte.
In den paar Minuten, die mir noch blieben, bis mein Taxi kam, skizzierte er soweit ich mich erinnere ganz grob die Problematik, die ich beim letzten Mal erklärt habe: Wie findet man heraus, mit welcher Beinstellung ein T. rex in der Schrittmitte die kleinste Muskelkraft brauchen würde?
Als ich wieder zurück war, gingen zwei Monate ins Land, in denen wir gelegentlich mails austauschten, aber ansonsten nicht viel passierte – ich hatte eine neue Vorlesung zu halten und John musste Elefanten durch Thailand scheuchen um deren Biomechanik zu verstehen. Aber im Sommer ging es dann schließlich richtig los, und die mails begannen zwischen Braunschweig und dem RVC hin- und herzusausen, dass man vermutlich auch gleich eine Extraleitung hätte legen können (der entsprechende Mailordner hat inzwischen mehr als 1000 Einträge – dank dieser Einträge kann ich die Geschichte hier auch relativ gut rekonstruieren). Aber keine Angst – ich werde nicht alle Details hier nacherzählen, sondern nur die grobe Story.
Das Matlab-Programm, mit dem John und sein Koautor seinerzeit die Berechnungen gemacht hatten, war wesentlich einfacher als ich ursprünglich gedacht hatte. Für eine gegebene Beinstellung dauerte eine Berechnung nur Sekunden – und davon ging der größte Teil für den Programmaufruf drauf. Es kostete wenig Mühe, ein kleines Progrämmchen zu schreiben, das verschiedene Beinstellungen ausprobiert – und nach ein paar Stunden Arbeit hatte ich statt den etwa 10 Beinstellungen aus Johns paper 1300 unterschiedliche berechnen und auswerten lassen.
Damit ihr selbst ein bisschen herumspielen könnt, habe ich ein kleines Java-Skript hochgeladen – ich hoffe, das klappt mit dem Blogsystem hier (in meiner Vorschau ging’s – falls es Schwierigkeiten gibt, bitte einfach nörgeln, dann schaue ich, dass ich die Dateien anderswo hochlade). Das Skript öffnet sich, wenn ihr aufs Bild klickt – am besten öffnet ihr es in einem neuen Fenster, dann könnt ihr parallel rumspielen und hier lesen.
Eigentlich ist das kleine Programm ziemlich simpel: In der Mitte seht ihr das Bein als Strichzeichnung – die Hüfte ist oben horizontal, unten die Zehen, dazwischen Ober- und Unterschenkel und Fuß. Die horizontalen Balken sind Meterbalken. Unten habt ihr drei Schieberegler, mit denen ihr den Winkel an der Hüfte, am Knie und am Knöchel einstellen könnt – der Winkel zwischen Mittelfuß und Zeh liegt dann fest, weil die Zehen hier im Modell gerade gezeichnet werden. (In unserem echten Berechnungsmodell war da auch noch ein Winkel drin, weil ein T. rex sicherlich irgendeine Art von Fersenpolster hatte.) Man braucht ein bisschen Übung, um sinnvolle Konfigurationen hinzubekommen, weil ich zu faul war, alles so zu programmieren, dass man direkt die Beinsegmente anklicken kann. Oben werden die Winkel und ein paar Koordinaten angezeigt. Ein perfekt durchgestrecktes Bein bekommt ihr zum Beispiel mit den Werten (90,180,180) für (Hüftwinkel, Kniewinkel, Knöchelwinkel).
Und? Seid ihr bereit für ein bisschen echte Dino-Forschung zum mitmachen?
In meiner ersten Rechnung habe ich also die drei Winkel für Hüfte, Knie und Knöchel jeweils in Schritten von 5° variiert und die Konfiguration gesucht, mit der sich (mit dem Rechenmodell vom letzten Mal) die kleinste Muskelmasse ergibt.
Das Optimum ergab sich für (60, 150,180) – der untere Teil des Beins ist also vollkommen gestreckt und nur der Oberschenkel kippt nach hinten, damit der Schwerpunkt über dem Fuß liegt (der liegt hier etwa 57 Zentimeter vor dem Hüftgelenk; später haben wir auch das variiert). Diese Pose ist zum Laufen sicher nicht geeignet – in der Schrittmitte soll das Bein ja eingeknickt sein, um sich abstoßen zu können.
Aber es gab ein paar ebenfalls ganz gute Posen, wo das Bein deutlich geknickter war, zum Beispiel (60, 140, 150) – eine ziemlich weit nach hinten gelehnte Pose -, oder (40, 110, 150) – eine Pose, die denen, die John in seinen Arbeiten verwendet hatte, durchaus ähnlich war, auch wenn der Schwerpunkt relativ weit hinten liegt. In seinen 2004-papern hatte John ja eine minimale Muskelmasse von mehr als 50% für eine Reaktionskraft vom 2,5fachen Körpergewicht berechnet. Mit meinem kleinen Progrämmchen ließ sich dieser Wert auf etwa 35% drücken, das sah ja schon ganz vielversprechend aus.
Allerdings gab es auch sehr seltsame Posen – beispielsweise die stark zurückgelehnte, oder die mit sehr geradem Bein. Wir brauchten also zusätzliche Bedingungen, um plausible Posen aus der Vielzahl der denkbaren herauszufiltern. Beispielsweise sollte in der Schrittmitte der Schwerpunkt über dem Fuß liegen. Beim Laufen darf das Bein auch nicht zu gestreckt sein.
Beim Diskutieren über solche zusätzlichen Randbedingungen merkte ich schnell, dass ich absolut keine Lust hatte, das alles in Matlab zu programmieren – meine Lieblingssprache ist C++. Mit objektorientierter Programmierung würde es bestimmt viel leichter sein, das Problem übersichtlich zu halten. Außerdem fingen wir an, darüber nachzudenken, wie man aus diesen Werten auf Geschwindigkeiten zurückschließen könnte.
Ein paar Wochen später hatte ich eine erste Programmversion fertig – da der lästige Matlab-Aufruf wegfiel, beschleunigte sich die Rechnung noch einmal um einen Faktor 10000 und statt einer Stunde brauchte ich nur noch ein paar Sekunden für deutlich mehr Konfigurationen. (Nebenbei bemerkt: Angefangen hat die Geschichte mit Johns Frage nach meinen Kenntnissen in Sachen Optimierungsalgorithmen – die brauchte ich hier aber gar nicht, weil die Rechnung so schnell war, dass man den gesamten Raum aller möglichen Beinstellungen abklappern konnte; selbst solche absurden wie (20, 30,180). Wie sagte Einstein (mehr oder weniger genau zitiert): Wenn wir wüssten, was am Ende rauskommt, wäre es keine Wissenschaft.)
Mit der neuen Version fand ich wiederum ein paar vielversprechende Posen. Besonders gut war beispielsweise (40, 115,180) – eine seltsam aussehende Pose, bei der der Fuß durchgestreckt ist und das ganze untere Bein nach vorn kippt (ich hoffe, ihr klickt fleißig im Beinkonfigurator herum – eigentlich ein toller Trick, so spare ich mir die vielen Bilder, die ich sonst machen müsste…) Diese nach vorn gekippten Beinstellungen sollten uns immer wieder begegnen – bis schließlich Steve Gatesy (der später dazukam) ein Argument fand, das sie definitiv ausschloss.
Aber auch ganz “vernünftig” aussehende Stellungen waren dabei, zum Beispiel (52, 124, 157). (Inzwischen war ich bei Ein-Grad-Schritten für die Winkel angekommen – das machte dann 729000 Simulationsrechnungen…) Diese würde etwa eine Muskelmasse von 20% des Körpergewichts pro Bein brauchen, also insgesamt 40% statt des alten Werts von über 50%, um eine Reaktionskraft von 2,5facher Körpermasse, eine Froudezahl von 16 (und damit Geschwindigkeiten in der Größenordnung von 70km/h) zu erreichen. (Zur kurzen Erinnerung; die Froudezahl war eine dimensionslose Zahl, die es erlaubt, die Geschwindigkeit unterschiedlicher Tiere “fair” zu vergleichen.) Immer noch etwas viel, aber unser T. rex würde zumindest nicht völlig langsam sein. Falls der Schwerpunkt dichter am Hüftgelenk liegen sollte, dann würde das die Masse nochmal ein wenig verkleinern.
Um das ganze etwas übersichtlicher zu bekommen und die Abhängigkeit von der (ja nicht genau bekannten) Position des Schwerpunktes besser zu verstehen, sind wir folgendermaßen vorgegangen. Wir haben die Schwerpunktkoordinate in 5cm-Schritten variiert, von kurz vor dem Hüftgelenk bis zu 80cm vor dem Hüftgelenk. Für jede Schwerpunktkoordinate haben wir die notwendige Muskelmasse berechnet, die man für eine Reaktionskraft (GRF) von 1*Körpermasse braucht. (Wenn man dann GRF=2 wissen will, dann muss man alle Massen mal 2 nehmen, weil die Abhängigkeit proportional ist.)
Damit die Position auch eine echte Laufposition ist, und kein gerades Stehen, haben wir zusätzlich gefordert, dass das Bein um mindestens 10% seiner Länge eingeknickt sein muss. Wenn man all das tut, ergibt sich diese Grafik:
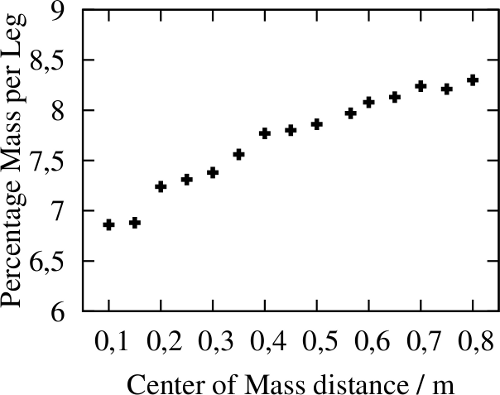
Auf der horizontalen Achse ist die Schwerpunktkoordinate aufgetragen, auf der vertikalen die Muskelmasse, die man für einen Wert von GRF=1 braucht. Wenn ihr also ein GRF von 2 wollt und der Schwerpunkt 50cm vor dem Hüftgelenk liegt, dann braucht ihr eine Muskelmasse von knapp 16% – pro Bein, versteht sich. Für eine Schwerpunktposition von 40cm vorm Hüftgelenk ist die beste Konfiguration (53, 120,156), bei Schwerpunktposition 0.565 (den Wert habe ich genommen, weil er in Johns altem paper verwendet wurde) ist es (50, 123, 162).
Die notwendige Muskelmasse für einen Wert von GRF=1 liegt also irgendwo zwischen etwa 7 und 8,7%.
Wie sollte man jetzt aus diesen Muskelmassenwerten auf eine Geschwindigkeit kommen? Unser Ansatz hierfür war folgender: Man macht eine Annahme über die maximal zulässige Muskelmasse pro Bein (beispielsweise 15% – das würde bedeuten, das 30% der Körpermasse in den Beinmuskeln stecken; und zwar nur in den Beinstreckern. Beim Strauß liegt der Wert, wenn ich mich recht entsinne, auch bei etwa 30%, aber der hat auch keinen großen Kopf und Schwanz. 30% sind also eine plausible – eher zu große – Obergrenze.) Da wir die notwendige Muskelmasse für GRF=1 kennen, können wir den maximalen GRF-Wert dann einfach ausrechnen, so wie eben schon erläutert. Da wir wissen, dass für GRF=1 die Muskelmasse zwischen 7 und 8.7% liegt, ergibt sich folgende Grafik:
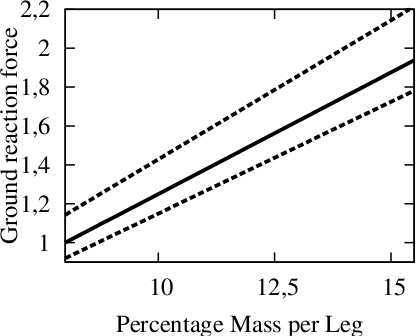
Hier könnt ihr jetzt direkt ablesen, in welchem Bereich GRF liegt, wenn ihr eine Annahme über die Muskelmasse eines Beins macht. Nehmen wir also den Wert von 15% Muskelmasse pro Bein (wie beim Strauß), dann liegt der Maximalwert der GRF irgendwo zwischen etwa 1,7 und 2,1.
Um von da aus zu einer Geschwindigkeit zu kommen, kann man zunächst die Beziehung vom letzten Mal verwenden, die GRF mit dem “duty factor” (also der prozentualen Bodenkontaktzeit) verknüpft. Bei einem Wert der GRF von 1.6 war der duty factor ja gerade 0.5 (ein Bein kommt in Bodenkontakt, wenn das andere den Boden verlässt) – die maximale GRF hier ist ein bisschen größer, also können wir erwarten, dass ein T. rex beim Laufen mit höchster Kraft tatsächlich eine Schwebphase erreichen würde, in der kein Fuß den Boden berührt.
Damit hat man aber immer noch keine Geschwindigkeit. Denn man weiß ja z.B. noch nicht, wie hoch die Schrittfrequenz war, die spielt aber natürlich eine wichtige Rolle. Zwei Möglichkeiten boten sich an: Zum einen gibt es Daten von Straußen, die mit duty-Faktoren (gruselige germische Wortkonstruktion) bis zu kleinen Werten von etwa 0.4 gerannt waren (bei Geschwindigkeiten von etwa 7m/s, was für einen Strauß noch bei weitem keine Höchstgeschwindigkeit ist).
Nimmt man diese Datenpunkte und rechnet sie entsprechend (über die Froude-Zahl) auf die Beinlänge eines T. rex um, dann kann man jetzt aus dem duty factor (und damit aus der GRF) eine Geschwindigkeit machen:
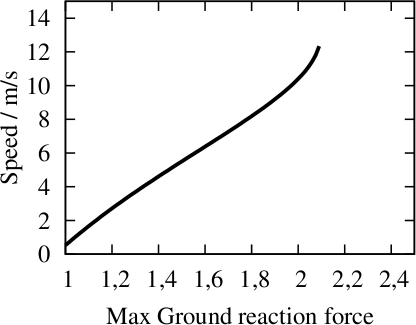
Die Kurve knickt am Ende nach oben ab, weil dort die Messpunkte bei den Straußen recht ungenau wurden – ob dieser Knick also sehr verlässlich ist, ist zweifelhaft.
Kombiniert man jetzt diese Grafik mit der vorigen, so ergibt sich die Geschwindigkeit als Funktion der Muskelmasse je Bein, mit einer Bandbreite, die durch die Schwerpunktsposition kommt:
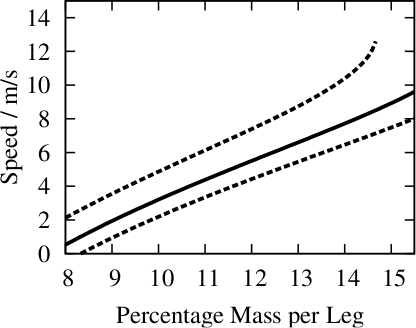
Wenn ihr also eine Muskelmasse von 12% des Körpergewichts je Bein für realistisch haltet, dann liegt die Höchstgeschwindigkeit zwischen etwa 4m/s (wenn der Schwerpunkt sehr weit vorn liegt) und etwas mehr als 7m/s (wenn der Schwerpunkt dicht an der Hüfte liegt). Erlaubt ihr 14%, dann ist die Höchstgeschwindigkeit im günstigsten Fall so etwa 10m/s – also knapp 40km/h.
Die andere Möglichkeit zum Abschätzen der Geschwindigkeit ist ein bisschen trickreicher, deswegen skizziere ich nur die Idee: Der duty factor sagt uns, wie lang der Bodenkontakt ist (in Prozent der Schrittdauer). Da die Vorwärtsgeschwindigkeit beim Laufen ungefähr konstant bleibt, muss man sich also fragen, wie weit das Bein kommen kann, während es in Bodenkontakt ist. Maximal kann es am Anfang sehr gestreckt sein, wenn der Fuß aufsetzt (probiert zum Beispiel mal (43, 170,180)), am Ende des Schrittes ist es ebenfalls sehr gestreckt (vielleicht (120,170,180)). Dazwischen muss der Schwerpunkt aber immer niedriger liegen als am Anfang und am Ende – und mit dieser Idee kann man eine geometrische Obergrenze für die Schrittlänge bekommen. Wenn nämlich das Bein sehr flach aufsetzt, dann ist in der Schrittmitte der Schwerpunkt sehr tief, aber dann braucht der T. rex auch eine besonders hohe Muskelmasse. Nimmt man wieder an, dass das Bein in der Schrittmitte um 10% eingeknickt ist, dann kann der Schwerpunkt beim Aufsetzen und Abstoßen nicht niedriger sein.
Die Schrittfrequenz schätzt man, indem man sie beim Strauß abguckt und entsprechend skaliert. Wenn man das alles durchrechnet, dann stellt man fest, dass sich höhere Geschwindigkeiten ergeben als mit der anderen Methode (die tatsächliche Geschwindigkeit ist natürlich immer die kleinere von beiden, weil ja beide Bedingungen erfüllt sein müssen.). Hier die beiden im Vergleich:
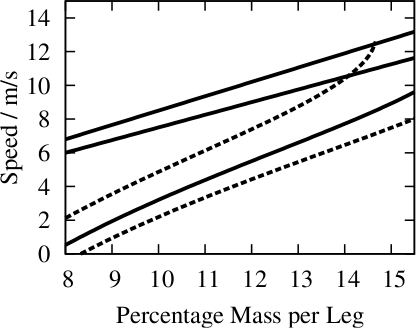
Wesentlich höher als 10m/s liegt die Spitzengeschwindigkeit auch hier nicht – praktischerweise liefert diese zweite Methode gerade bei hohen Muskelmassen eine gute obere Grenze, wo die erste Methode versagt.
Diese Simulationen zeigen also folgendes: Ein T. rex mit hinreichend muskulösen Beinen kann beim Laufen eine kurze Schwebphase erreichen. Die Geschwindigkeit, die er erreichen kann, hängt von der Schwerpunktsposition ab, dürfte aber maximal bei etwa 40km/h liegen. Es sind natürlich ein paar Unwägbarkeiten in dieser Abschätzung drin – beispielsweise die Umrechnung über die Ähnlichkeit mit dem Strauß. Im absoluten Optimalfall (der aber nicht soo wahrscheinlich ist) könnte die Geschwindigkeit also auch ein bisschen drüber liegen (der T. rex von Jurassic Park hatte ja 52km/h – das dürfte dann aber wirklich das absolute Ende der Fahnenstange sein). 70 Stundenkilometer und mehr, wie einige Forscher angenommen hatten, waren also wohl ziemlich definitiv nicht drin. Aber ein 6-Tonnen-Raubsaurier mit 40km/h ist auch nicht gerade zu verachten – Elefanten erreichen (auch wenn es oft behauptet wird) solche Geschwindigkeiten nicht (irgendwann muss ich wohl auch mal erzählen, was John so alles beim Elefantenscheuchen herausgefunden hat).
Das war ja schon ein schönes Stückchen Arbeit. Zusätzlich habe ich mir noch den Spaß gemacht, die (aus der Rechnung sowieso bekannten) Biegemomente auf die Knochen anzusehen und zu prüfen, dass diese nicht größer werden als die Knochenfestigkeit es zulässt (vielleicht erinnert ihr euch, dass ich die Knochenfestigkeit in Teil I schon mal erwähnt hatte – hier haben wir jetzt den Vorteil, dass wir die wirkenden Momente abhängig von der Beinstellung genau kennen). Aus dieser Rechnung (in die natürlich auch die Knochenform eingeht, aber die haben andere ja schon vermessen) ergab sich (für eine Konfiguration von (50,123,162)) ein Maximalwert der GRF von 2,5 (wobei ich einen Sicherheitsfaktor angenommen habe, wie er bei springenden Hunden gemessen wurde). Die Knochenfestigkeit ist hier also nicht der limitierende Faktor – umgekehrt scheinen die Knochen aber auch nicht gigantisch überdimensioniert zu sein, was dann wiederum das Vertrauen in die Rechnung selbst stärkt.
Und schließlich habe ich noch ein andere kleine Abschätzung gemacht: Man kann ja vermuten, dass ein Grund für die kleinen Arme eines T. rex genau darin besteht, dass er seine Frontmasse verringert, um seinen Schwerpunkt nach hinten zu bekommen. Quantitativ zeigt sich, dass sich dadurch (ich nahm eine Reduzierung der Armmasse um 30kg an) die notwendige Muskelmasse (für einen plausiblen Datensatz) von 8% der Körpermasse auf etwa 7,9% der Körpermasse verringert – ob das ein hinreichender evolutionärer Druck ist, ist natürlich schwer zu beurteilen, aber immerhin sieht man, dass sich auch solche Probleme prinzipiell durch Rechnung in den Griff bekommen lassen.
Alles in allem war das – ich hoffe, da stimmt ihr zu – eine recht runde Sache geworden. Wenn ihr in das von mir mit-geschriebene paper reinguckt, werdet ihr allerdings feststellen, dass diese Rechnungen dort so gar nicht vorkommen – sie wurden nämlich in dieser Form nie veröffentlicht. (Hier bekommt ihr also neue, bisher unveröffentlichte wissenschaftliche Ergebnisse auf den Scienceblogs!) Der Entwurf einer Veröffentlichung war (in Stichworten) schon ziemlich weit gediehen und ich nahm an, dass sie irgendwann im Sommer 2006 fertig sein würde. Aber dann kam alles ganz anders…
…und das erzähle ich dann natürlich im vierten Teil. (Warum werden Artikelserien eigentlich immer länger als man denkt?)






Kommentare (17)