Es klingt verrückt, aber es stimmt: manchmal werden Metalle fester, wenn sie Nichts enthalten. Oder genauer gesagt, wenn sie winzige Löcher haben.
Um das zu verstehen, müssen wir einen kurzen Blick darauf werfen, wie Metalle sich plastisch verformen. Ausführlich habe ich das schon vor längerer Zeit erklärt, deswegen gibt es hier nur eine Kurzfassung:
Metalle enthalten immer Störungen, die man Versetzungen nennt. An diesen Störstellen ist das Kristallgitter eben gestört, wie zum Beispiel in diesem Bild:
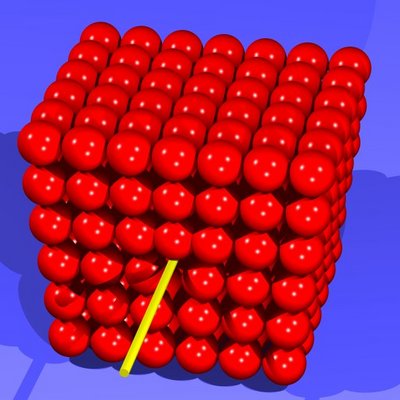
Die gelbe Linie zeigt die Linie der Störung, eben die Versetzung. Versetzungen können sich relativ leicht durch den Kristall bewegen und scheren dabei Atome oberhalb der Versetzungslinie gegen Atome darunter ab. Wenn eine Versetzung durch einen Kristall läuft, dann sorgt sie damit für eine winzig kleine plastische Verformung, also eine Verformung, die bleibt, auch wenn man die Last wegnimmt.
Wenn ihr den atomaren Mechanismus dahinter verstehen wollt, folgt einfach dem Link oben. Wie so oft in der Wissenschaft muss man aber gar nicht immer zurück zur fundamentalen Erklärungsebene – man kann sich die Versetzung auch modellhaft als eine Linie vorstellen, die sich durch den Kristall bewegt, wenn eine Kraft auf sie wirkt, ein bisschen so, als würde man einen Faden durch ein Glas mit Honig ziehen. (Wieder mal ein gutes Beispiel für das Denken in Modellen.)
Ein Metall enthält ziemlich viele solcher Versetzungen – wenn man alle Versetzungslinien in einem Kubikzentimeter eines stark verformten Metalls aneinanderreihen würde, käme man etwa einmal von der Erde zum Mond und wieder zurück. Hier seht ihr mal ein Simulationsbild der Versetzungen in einem Metall (die Details sind nicht so wichtig, hier geht es nur darum, dass ihr das Gewusel erkennt):
Legt man an ein Metall eine mechanische Spannung an (indem man zum Beispiel dran zieht), dann bewegen sich die Versetzungen, wenn die Spannung groß genug ist und scheren das Metall ab. Das passiert beispielsweise, wenn ihr einen Draht oder eine Büroklammer verbiegt.
Dabei entstehen übrigens auch neue Versetzungen – und weil sich die Versetzungen gegenseitig im Weg sind und sich behindern, wird das Metall an dieser Stelle fester. Deswegen ist es auch leicht, einen geraden Draht krumm zu biegen, aber gar nicht so leicht, ihn wieder geradezubekommen – genau da, wo man zurückbiegen müsste, ist das Material fester als drum herum, deswegen biegt es sich meist eher an anderen Stellen.
Wenn ihr besonders feste Metalle herstellen wollt, die sich also nicht so leicht plastisch verformen, dann müsst ihr die Versetzungen an ihrer Bewegung hindern. Sich dafür Tricks einfallen zu lassen, ist letztlich eines der Hauptbetätigungsfelder für MaterialwissenschaftlerInnen. Es gibt verschiedene solcher Mechanismen (das Metall vorzuverformen ist einer, den wir gerade gesehen haben), von denen wir jetzt aber nur einen einzigen brauchen.
Auch wenn wir sie uns nicht auf der atomaren Ebene angucken – die Versetzungen laufen innerhalb des Kristallgitters. Kleine Teilchen mit einer anderen Kristallstruktur können deshalb die Versetzung behindern, weil sie nicht in diese Teilchen eindringen kann und sie irgendwie “umwandern” muss. Bei hohen Temperaturen passiert das durch einen Mechanismus, den man “Klettern” nennt (und dessen Details hier nicht so wichtig sind).
Dieses Bild (habe ich meinem Chef geklaut [unschuldig-pfeif]) zeigt, wie man sich das vorstellen kann:
Die Versetzung kommt von links, trifft auch zwei Teilchen und muss über sie hinüber”klettern”. Dann löst sie sich von den Teilchen wieder ab. Dieser Klettermechanismus ist vor allem bei hohen Temperaturen wichtig – bei niedrigen Temperaturen können Versetzungen nicht so gut klettern und kommen noch schwerer an solchen Hindernissen vorbei; das ist ein Grund dafür, dass Metalle mit zunehmender Temperatur an Festigkeit verlieren.
Da eine Versetzung ja eine Störung des Kristallgitters ist, hat sie auch eine bestimmte Energie, denn sie verzerrt den Kristall. Diese Energie kann an dem Teilchen höher oder geringer sein – je nachdem, was das Teilchen für Eigenschaften hat. Ist die Energie höher, dann bleibt die Versetzung vor dem Teilchen hängen, ist sie niedriger, dann braucht man zusätzliche Energie (also zusätzliche Kraft), um die Versetzung wieder vom Teilchen zu lösen.
Und jetzt stellt euch vor, wir nehmen das Teilchen weg und ersetzen es durch – nichts. Wir machen also einfach kleine Löcher in unseren Kristall. Wenn eine Versetzung auf so ein kugelförmiges Loch zuläuft, dann kann sie dort natürlich nicht rein – denn eine Störung des Atomgitters kann sich nicht dort aufhalten, wo kein Atomgitter ist. Am Loch ist die Energie der Versetzung aber auf jeden Fall niedriger als im Kristall selbst, denn im Loch ist ja kein Material, das von der Versetzung irgendwie verzerrt werden könnte. Man braucht also auch hier eine Extra-Kraft – die Versetzung fühlt sich am Loch viel wohler als anderswo im Kristall und man muss sie quasi mit der Brechstange losreißen.
So, nun wisst ihr, wie man mit Nichts Metalle verstärkt. Bleibt nur ein kleines Problem: Wo kriegen wir das “Nichts” her? Damit der Mechanismus effektiv wirken kann, müssen die Löcher sehr winzig sein – möglichst nur einige Nanometer im Durchmesser. Wie soll man solche Löcher in den Kristall bekommen – Bohren scheidet ja wohl aus? Gibt es solche Materialien überhaupt?
Ja, die gibt es tatsächlich – falls ihr noch energiefressende Glühlampen habt, dann habt ihr ein Beispiel dafür direkt in der nächsten Lampe:

Von Lander777 – https://en.wikipedia.org/w/index.php?title=File:Filament.jpg&action=edit, Gemeinfrei, Link
Wolfram-Legierungen (aus denen man ja die Glühfäden macht) werden nämlich mit diesem Mechanismus verstärkt. Und dazu verwendet man einen genial einfachen Trick: Man legiert Wolfram mit Kalium. Das Kalium bildet – bei geeigneter Behandlung der Legierung – sehr feine Teilchen im Wolfram.
Nun ist Kalium nicht “Nichts” – aber Kalium hat einen sehr niedrigen Schmelz- und Siedepunkt, es verdampft bei 759°C. In einem Glühfaden ist es wesentlich heißer als das – die kleinen Kaliumteilchen verdampfen also. Da sie aber ja im Wolfram eingeschlossen sind, können sie nicht raus und bilden winzige Dampfbläschen. Da das Kalium jetzt gasförmig ist, wirkt die Dampfblase wie ein Hohlraum für die Versetzungen – sie können nicht in die Blase eindringen, und für sie ist die Kaliumblase einfach nur “Nichts”.
Die Kaliumbläschen sind übrigens ein Grund dafür, dass Glühlampen eine sehr begrenzte Lebensdauer haben: Durch Diffusion des Kaliums im Wolfram können die Bläschen im Laufe der Zeit zusammenwachsen und sich so vergrößern. Dabei nimmt zum einen ihre verfestigende Wirkung ab (bei diesem Mechanismus ist es besser, viele kleine Teilchen zu haben als wenige große), zum anderen können größere Dampfblasen dann auch als Schwachstellen wirken.
Wie ihr seht, ist es tatsächlich möglich, Metalle mit “Nichts” zu verstärken – und wir wenden diesen Trick sogar täglich an.






Kommentare (26)