“Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.”
Dieses Zitat von Minkowksi, das in kaum einen Buch zur Relativitätstheorie fehlen darf, enthält eine der Kernaussagen der SRT: Raum und Zeit werden gemischt, man spricht besser von der Raum-Zeit.
Einstein selbst fand das Zitat anfänglich übrigens nicht so toll – später, in der Allgemeinen RT, vertrat er dann aber ähnliche (allerdings noch radikalere) Ansichten.
Bevor jemand Einspruch erhebt: Nein, die Relativitätstheorie ist nicht widerlegt, auch wenn wir da diese merkwürdigen Neutrinoexperimente haben. Selbst wenn sich zeigen sollte, dass die SRT “fehlerhaft” ist, so würden die bekannten Formeln (wie die Längenkontraktion oder die Zeitdilatation) weiterhin als Grenzfall gelten, dazu sind sie experimentell zu gut abgesichert.
Diese “Mischung” von Raum und Zeit zeigt sich zum Beispiel am Problem der Gleichzeitigkeit: Zwei Ereignisse, die für mich gleichzeitig sind, sind es zum Beispiel für Mark Brandis1, der mit hoher Geschwindigkeit in seiner Delta VII an mir vorbeibrettert, nicht unbedingt. Für mich trennt die beiden Ereignisse nur “Raum”, aber für den guten alten Mark scheint eins der beiden Ereignisse zeitlich vor dem anderen stattzufinden. Mein “Raum” ist für ihn eine Mischung aus “Raum” und “Zeit”. (Über Raumzeit habe ich ja schon mal einiges geschrieben.)
1Es muss ja nicht immer Perry Rhodan sein; und die Mark-Brandis-Bücher wurden vor kurzem ja neu aufgelegt – auch wenn die Höchstgeschwindigkeit der Delta VII natürlich weit unter der Lichtgeschwindigkeit liegt…
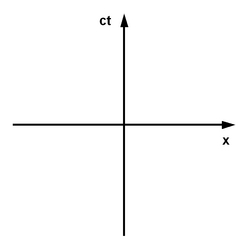
Eine praktische Methode, das zu veranschaulichen, sind Minkowski-Diagramme wie dieses hier (die habe ich neulich schon ausführlich erklärt, deswegen hier nur die – bei mir selbst geklaute – Kurzfassung):
Darin ist die senkrechte Achse die Zeit und die waagerechte Achse der Ort. Auf der vertikalen Achse steht dabei ct, also Lichtgeschwindigkeit mal Zeit – weil man mit Hilfe der Lichtgeschwindigkeit zwischen Zeiten und Strecken hin- und herrechnen kann. (Man rechnet also praktisch Zeiten in “Lichtmetern” (1Lm=1/300000000s).)
Das Tolle an Minkowski-Diagrammen ist, dass man ganz einfach ein Koordinatensystem für ein (mit konstanter Geschwindigkeit) bewegtes Objekt einzeichnen kann. Der Trick ist ganz einfach. Wen sich die Delta VII mit konstanter Geschwindigkeit bewegt, dann ist ihre Weltlinie eine schräg verlaufende also geneigte Gerade. Diese Gerade hat einen Winkel zu unserer senkrechten Achse. Sie entspricht deshalb der Zeitachse der Delta VII, deswegen beschrifte ich sie mit ct’:
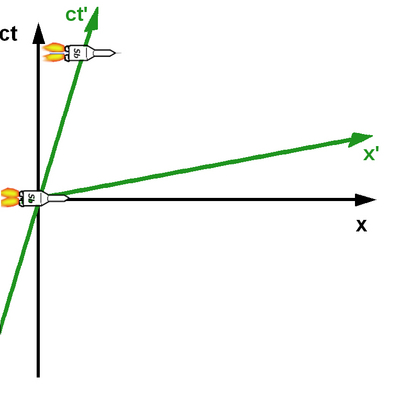
In das Diagramm habe ich auch die neue x’-Achse eingezeichnet – man bekommt sie aus der alten x-Achse, indem man sie um denselben Winkel rotiert – nur in entgegengesetzter Richtung.
Alle Punkte auf der grünen x’-Achse sind jetzt für Mark B. Ereignisse, die gleichzeitig stattfinden – während sie das für uns auf den Erdboden nicht tun. Dank des Minkowksi-Diagramms kann man leicht sehen, wie bestimmte Ereignisse in unterschiedlichen Bezugssystemen ablaufen.
Stellen wir uns beispielsweise vor, dass irgendwo rechts im Bild zu einem bestimmten Zeitpunkt eine Explosion stattfindet:
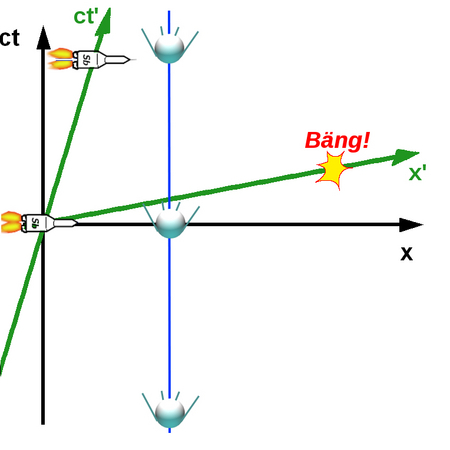
Von uns (da, wo der Satellit eingezeichnet ist) aus gesehen, passiert dies, nachdem das Raumschiff am Punkt Null (da, wo sich die schwarzen Linien kreuzen) durchgeflogen ist, aber vom Raumschiff aus gesehen sind beide Ereignisse genau gleichzeitig.
Raum und Zeit werden also miteinander vermischt, zwei Ereignisse, die aus Sicht von Mark B. nur “Raum” trennt, trennen aus unserer Sicht “Raum” und “Zeit”. Das bedeutet auch (und das ist der “Trick”, den wir in der QFT öfters verwenden werden): Wenn wir etwas über die Zeitabhängigkeit einer Größe wissen, dann können wir daraus gewisse Rückschlüsse darüber ziehen, wie sie vom Ort abhängt.
Und das war ja genau der Grund, warum man der Schrödingergleichung, wie im ersten Teil erwähnt, sofort ansehen kann, dass sie nicht relativistisch ist, denn in ihr stecken Ort und Zeit in unterschiedlichen Ableitungen.
So wie Raum und Zeit vermischt werden, werden auch andere Größen vermischt. Nehmen wir beispielsweise die elektrische Ladung. Wenn ich neben mir einen gleichmäßig geladenen Draht liegen habe, dann hat dieser eine bestimmte Ladung, genauer gesagt, eine Ladungsdichte (also Ladung pro Volumen). Wenn der Draht ruht, ruhen auch die Ladungen im Draht.
Mark B. dagegen sieht die Sache ganz anders: Zum einen misst er zwar dieselbe Ladung, allerdings wegen der relativistischen Längenkontraktion auf einer kürzeren Drahtlänge – er sieht also eine höhere Ladungsdichte. Zusätzlich scheint es für ihn so, als würde der Draht an ihm vorbeisausen – er sieht also zusätzlich auch noch einen elektrischen Strom. Ladung und Strom (genauer gesagt: Stromdichte) werden also ebenfalls vermischt, genauso wie Zeit und Raum (und es gelten sogar dieselben Formeln). Es ist übrigens eine beliebte Aufgabe für Physik-Studis, zu zeigen, dass man das magnetische Feld eines Drahtes, in dem ein Strom fließt, auch über die Längenkontraktion der Ladungsdichte herleiten kann. Dieses Bild hier illustriert das Prinzip:
Wenn sich die Elektronen bewegen, dann sieht es vom Draht (mit ruhenden positiven Ladungen) aus so aus, als wären sie enger zusammengerückt – deswegen ziehen sich zwei stromführende Drähte an. Die Elektronen sehen umgekehrt die positiven Ladungen als enger zusammengerückt. Diese Anziehung zwischen zwei Drähten erklärt man normalerweise mit Hilfe des Magnetfeldes, aber man kann sie auch über die Lorentzkontraktion verstehen.
Müssten dann nicht auch das elektrische und das magnetische Feld irgendwie nach dieser Logik zusammenhängen? Ja, das tun sie auch. Allerdings nicht ganz direkt, sondern mit Hilfe der sogenannten Potentiale. Zu einem elektrischen Feld einer ruhenden Ladung gehört ein elektrisches Potential (das man aus dem Alltag als elektrische Spannung kennt). Bewegt sich die Ladung (oder bewegt man sich relativ zur Ladung – nicht umsonst heißt es ja “Relativitäts”-Theorie), dann kommt ein weiteres Potential hinzu, das Vektorpotential, das eng mit dem Magnetfeld zusammenhängt. (Die genaue Beziehung kann uns hier egal sein.)
(Zum Vektorpotential gibt es auch eine interessante Geschichte: In der klassischen Elektrodynamik wurde es als reine Rechengröße ohne jede “echte” Bedeutung eingeführt, aber in der Quantenmechanik zeigt sich, dass das Vektorpotential die Wellenfunktionen von Elektronen beeinflussen kann. Das ist der berühmte Aharonov-Bohm-Effekt. Als ich mal in Boston am Physik-Institut war, durfte ich übrigens im Büro von Aharonov sitzen – leider war er selbst nicht da.)
Elektrisches und Vektorpotential gehören also genauso zusammen wie Zeit und Raum oder Ladung und Strom.
Auch bei Wellen gibt es so eine Vermischung (und Wellen spielen in der QFT eine wichtige Rolle). Eine Welle wie diese hier
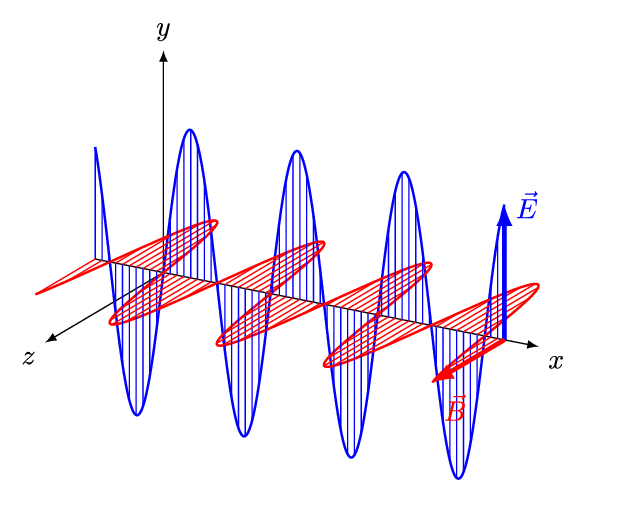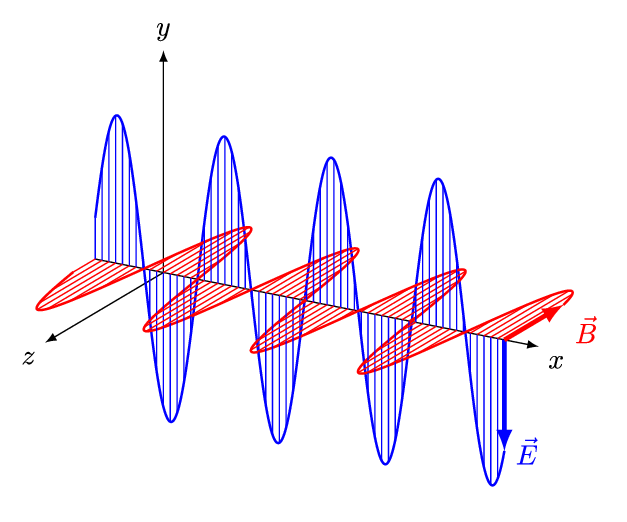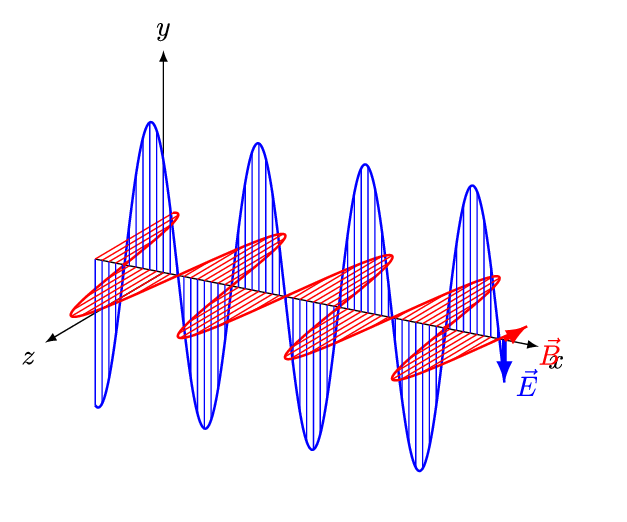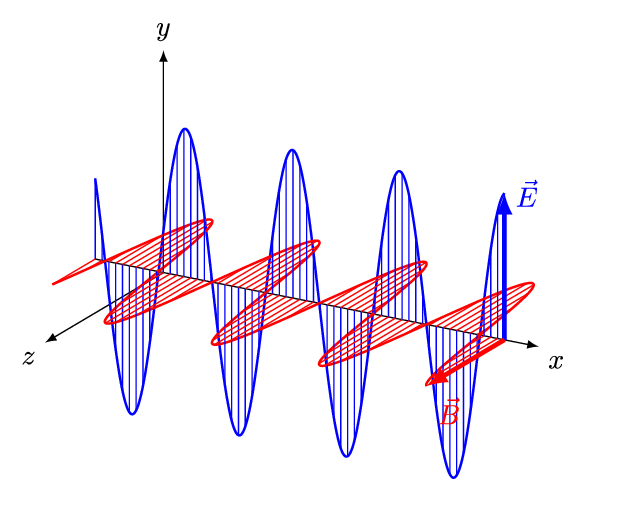
Von And1mu – Eigenes Werk, CC-BY-SA 4.0, Link
hat eine Wellenlänge und eine Frequenz. Zeichnet man die Wellenberge in ein Minkowski-Diagramm ein, dann sieht man, dass Mark B. an Bord seiner Delta VII wegen der Längenkontraktion und der Zeit-Dilatation eine andere Wellenlänge und eine andere Frequenz sieht, allerdings dieselbe Geschwindigkeit (wenn es sich um eine elektromagnetische Welle handelt, die sich mit Lichtgeschwindigkeit ausbreitet). Schreibt man statt der Wellenlänge den Kehrwert der Wellenlänge (die sogenannte Wellenzahl), dann gilt für Frequenz und Wellenzahl wieder derselbe Zusammenhang wie für Zeit und Ort.
Typischerweise baut man noch den einen oder anderen Faktor von 2π ein und verwendet die Kreisfrequenz ω = 2 π Frequenz und die Wellenzahl k=2 π / λ. Die Extra-π’s hier spart man sich dafür später anderswo wieder ein.
Noch ein fünftes Größenpaar gibt es, das in ähnlicher Weise vermischt wird wie Raum/Zeit, Ladung/Ladungsdichte, Potential/Vektorpotential, Frequenz/Wellenlänge. Dabei handelt es sich um Energie und Impuls.
Nehmt als Beispiel ein Teilchen, das ruhig neben euch auf der Erde liegt. Es hat nach Einsteins berühmter Formel eine Energie von E=mc² und einen Impuls von Null. (Zur Erinnerung: Impuls ist gleich Masse mal Geschwindigkeit.) Für den vorbeifliegenden EAAU-Captain (für literarisch ungebildete: Das ist Mark Brandis) dagegen sieht es so aus, als ob sich das Teilchen mit hoher Geschwindigkeit bewegt. Zu seiner Ruheenergie kommt noch die kinetische Energie hinzu, und auch sein Impuls ist (betragsmäßig) größer als Null. Oft spricht man hier von einem relativistischen Massezuwachs, so dass die Formel E=mc² weiter gilt, nur eben mit erhöhter Masse, und so dass man auch die klassische Formel Impuls gleich Masse mal Geschwindigkeit verwenden kann. Ich finde diese Formulierung allerdings ein bisschen verwirrend und werde, wenn ich Masse sage, immer die Ruhemasse eines Teilchens meinen, also die Masse, die ihr messt, wenn ihr euch relativ zum Teilchen nicht bewegt. (Warum Teilchen überhaupt eine Masse haben, werden wir auch noch diskutieren.)
Es gilt die berühmte Energie-Impuls-Beziehung (ausnahmsweise mit Faktoren von c an der richtigen Stelle) E²=m²c⁴ + p² c² – dabei ist m die Ruhemasse, nicht die “relativistische” Masse.
Wir haben jetzt also fünf Größenpaare, die sich alle in ganz ähnlicher Weise verhalten: Zeit/Ort, Ladungsdichte/Strom, elektrisches Potential/Vektorpotential, Frequenz/Wellenzahl, Energie/Impuls. Ort, Strom, Vektorpotential, Wellenzahl und Impuls sind dabei Vektoren, also Größen, die einen Wert und eine Richtung haben (bei der Wellenzahl ist das so, wie ich sie oben eingeführt habe, nicht ganz offensichtlich, aber man nimmt hier als Richtung die Ausbreitungsrichtung der Welle). Im dreidimensionalen Raum (in dem leben wir ja – es sei denn, Ihr seid Stringtheoretiker…) braucht so ein Vektor drei Zahlen. (Das ist ja auch aus dem Alltag klar, um anzugeben, wo etwas auf der Erde ist braucht ihr Längengrad, Breitengrad und Höhe.) Da man einen Vektor (einen Auffrischungskurs “Was ist ein Vektor” findet ihr übrigens hier) mit einer vierten Größe (die sozusagen “Zeitcharakter” hat) zusammenfasst, spricht man oft auch von Vierervektoren. Das kann man dann so schreiben: (ct, x,y,z), oder (ct, x). Dabei ist t die Zeit und x,y,z sind die drei Zahlen für den Ort (die wir als Vektor x zusammenfassen können).
Der Faktor c am ct dient dabei, wie oben beim Minkowski-Diagramm erläutert, dazu, die Zeit einheitenmäßig in einen Strecke umzurechnen. Meistens werde ich mich der praktischen Konvention theoretischer Physikerinnen bedienen, und c=1 setzen (also alle Längen in Lichtsekunden oder Zeiten in Lichtmetern rechnen). Das ist so lange praktisch, bis man versucht, tatsächlich eine Zahl auszurechnen, dann darf man sich damit amüsieren, die fehlenden Faktoren wieder einzubauen.
Für Vierervektoren gelten spezielle Rechenregeln, die das Hantieren mit ihnen leichter machen. Insbesondere kann man mit Vierervektoren Größen berechnen, von denen man zeigen kann, dass sie für alle Beobachter denselben Wert annehmen. Ein Beispiel dafür ist der Raum-Zeit-Abstand zwischen zwei Ereignissen. Liegen die beiden Ereignisse in meinem Bezugssystem um eine Zeit Δt auseinander und haben einen räumlichen Abstand Δx, dann ist der Raumzeitabstand Δs definiert als Δs² = c² Δt² – Δx².
Dieser Raumzeitabstand ist eine zentrale Größe in der Speziellen Relativitätstheorie. Er hat also immer denselben Wert, egal in welchem Bezugssystem er gemessen wird.
Hier eine Übersicht über die Vierervektoren (werden wir vermutlich selten explizit benötigen, ich schreib sie hier trotzdem hin, weil ich immer vergesse, wo die c’s hingehören):
Zeit/Ort: (ct,x)
Ladungsdichte/Stromdichte: (cρ, j)
Potential/Vektorpotential: (φ/c, A)
Frequenz/Wellenzahl: (ω/c, k)
Energie/Impuls: (E/c, p)
(Warnung: Ihr seid hier immer noch im abgefahrenen Formelteil, der ist erst zuende, wenn ihr das Formel-Aufhebungszeichen seht…) Vierervektoren schreibt man typischerweise mit griechischen Indices, also zum Beispiel xμ für eine Komponente des Orts-Zeit-Vierervektors.
Multipliziert man zwei Vierervektoren miteinander, so werden die Zeit- und Raumkomponenten jeweils quadriert und voneinander abgezogen.
Dabei habe ich hier die Metrik (+—) verwendet, die Minus-Zeichen kommen also an die räumliche Komponente. Häufig wird das auch andersherum gemacht – da hat jedes Buch seine Lieblingskonvention. Deswegen werde ich sicherlich in nächster Zeit jede Menge falsche Vorzeichen in meine Formeln einbauen – damit ihr das korrigieren könnt, gibt es hier ein paar Minuszeichen, bei denen ihr euch bedienen könnt:
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
(Den Trick habe ich von meinem Doktorvater, der den Mathe-Vorkurs für Studienanfänger damit begann, einen Haufen Minuszeichen an die Tafel zu schreiben…)
Damit man sich bei den Vorzeichen nicht verheddert, verwendet man oft die Schreibweise mit ko- und kontravarianten Vektoren – dann schreibt man das Produkt als
mit
Man merkt sich das am besten mit der schönen η-Matrix
Mit der kann man die Indices von oben nach unten ziehen. Damit ist dann
Wer mit Ko’s und Kontra’s durcheinander kommt, kann sich den politischen Satz merken “Die Kontras sind oben.”
Aber keine Sorge, so im Detail werde ich mit ko- und kontravarianten Vektoren nicht rumrechnen (ich bin Weltmeister im Verheddern bei solchen Rechnungen) – ich schreibe das hier nur der Vollständigkeit halber hin. Ausführlicher erklärt das beispielsweise die Wikipedia oder das Gravitations-Buch von Misner, Thorne, Wheeler.
So, hier geht’s jetzt wirklich für alle weiter:
Bastelt man sich nun so eine unabhängige Größe aus Vierervektoren, so hat das einen großen Vorteil: Man kann sich jeweils in das Bezugssystem setzen, in dem die Rechnung besonders einfach ist (beispielsweise in das Ruhesystem eines Teilchens). Wenn eine solche unabhängige (man sagt auch “invariante”) Größe dort einen bestimmten Wert hat, dann hat sie ihn überall. Man rechnet also erst im “einfachsten” Bezugssystem, und danach geht man in das, das einen eigentlich interessiert.
Diesen Trick werde ich öfters mal verwenden – er spielt zum Beispiel eine zentrale Rolle bei der Frage, warum sich gleiche elektrische Ladungen abstoßen, aber Massen immer anziehen.
Und damit haben wir auch alles zusammengesammelt, was wir über Relativitätstheorie wissen müssen, um eine relativistische Quantenfeldtheorie basteln zu können. Als nächstes kümmern wir uns um Quanten.






Kommentare (50)