Und die Verwirrung wird all jene verwirren, die nicht wissen, mmhh… und niemand wird wirklich genau wissen, wo diese kleinen Dinge zu finden sind, die verknüpft sind mit einer Art von Handarbeitszeug, das durch die Verknüpfung verknüpft ist. Und zu der Zeit soll ein Freund seines Freundes Hammer verlieren. Und die Jungen sollen nicht wissen, wo die Dinge, die jene Väter erst um acht Uhr am vorhergehenden Abend dort hingelegt hatten, kurz vor Glockenschlag…
Am Ende des letzten Teils waren wir über eine seltsame Begriffsverwirrung gestolpert – Wir haben eine Wellengleichung gefunden, die aus der klassischen Physik kam, aber auch für Quantentheorien verwendet wurde. Haben wir es nun mit klassischen Feldern zu tun oder mit quantenmechanischen Wellen? Oder mit beidem?
Verwirrend oder?
Dies ist tatsächlich eine der zahlreichen Verwirr-Quellen in der Quantenfeldtheorie. Die Klein-Gordon-Gleichung für unser φ sieht ganz ähnlich aus wie die Schrödingergleichung für die Wellenfunktion ψ (Wenn ihr nicht wisst, was das ist: Erklär ich gleich). Ursprünglich hat man die beiden Gleichungen auch ganz ähnlich behandelt, aber tatsächlich sind es – so wie wir sie hier verwenden – zwei ganz unterschiedliche Dinge.
Bevor ich das noch etwas ausführlicher erkläre, muss ich wohl ein paar Worte zur Wellenfunktion verlieren – in unserer Pfadintegralformulierung gab es so ein Gebilde ja gar nicht.
Die Wellenfunktion
Implizit gibt es sie aber schon. Wir hatten ja gesehen, dass wir – für eine bestimmte Situation wie den Doppelspalt – die Amplitude (also die kleinen Pfeile) dafür ausrechnen können, das Elektron am Ort x zu finden. (Und die Wahrscheinlichkeit war das Quadrat der Amplitude.) Diese Größe hatte ich z.B. A(Q,x) genannt – die Wahrscheinlichkeitsamplitude dafür, dass das Elektron von der Quelle Q am Ort x ankommt (und zwar auch zu einer bestimmten Zeit, die steckte in unseren Pfaden ja immer mit drin).
Stellt euch nun vor, dass ihr ganz sicher wisst, dass das Elektron die Quelle Q zu einer bestimmten Zeit t0 verlässt. Dann könnt ihr A(Q,x) für alle späteren Zeitpunkte mit unserer Pfadintegralmethode ausrechnen. Weil ihr sicher wisst, dass das Elektron bei Q angefangen hat, könnt ihr dafür auch einfach A(x) schreiben – ihr wisst, dass das die Amplitude dafür ist, das Elektron bei x zu finden, denn eine andere Möglichkeit, dorthin zu gelangen, hatte es ja nicht – es musste ja bei Q starten.
Wenn ich nun für alle denkbaren Orte x die Größe A(x) zu einer Zeit kenne, dann weiß ich alles, was es über das Elektron zu wissen gibt. Es gibt eine Gleichung, mit der ich ausrechnen kann, wie groß die Amplitude an jedem Ort zu einem späteren Zeitpunkt ist. Kenne ich also die Amplitude A(x) zu einer Zeit t, kann ich sie zu einer späteren Zeit t’ berechnen.
Schrödinger hat genau diese Gleichung aufgestellt (allerdings nicht mit Pfadintegralen, sondern durch geschicktes Raten) – die Schrödingergleichung. Die Amplitude A(x,t) wird Wellenfunktion genannt und bekommt ein schickes ψ als Formelzeichen: ψ(x,t).
Feld oder Wellenfunktion?
Die Klein-Gordon-Gleichung habe ich hier für ein klassisches Feld φ hergeleitet, also eine Größe, die schon klassisch an jedem Raumzeitpunkt definiert ist. ψ ist dagegen die Wellenfunktion für ein quantenmechanisch beschriebenes Teilchen, das klassisch an einem Ort lokalisiert wäre.
Diese Verwirrung war in den 1920er Jahren auch bei den Physikern vorhanden – man versuchte zunächst, einfach eine Gleichung nach Art der Schrödingergleichung zu finden, die nur eben mit der Relativitätstheorie zusammenpasste. Die Klein-Gordon-Gleichung würde man dann entsprechend interpretieren, mit φ als einer Wellenfunktion, die also die Wahrscheinlichkeitsamplitude angibt. Dirac stellte eine ähnliche Gleichung (die Dirac-Gleichung) für das Elektron auf – diese Gleichung enthält eine Funktion ψ, die ganz ähnlich zur Wellenfunktion in der “normalen” Quantenmechanik ist. (Zur Dirac-Gleichung sage ich später noch etwas.)
Es zeigte sich aber bald, dass diese Vorgehensweise mit Schwierigkeiten verbunden ist. Heute können wir diese Schwierigkeiten leicht verstehen: Wenn die kinetische (also die Bewegungs-) Energie eines Teilchens groß genug ist, dann können Teilchen-Antiteilchen-Paare erzeugt werden. Beispielsweise können zwei Pionen – eine spezielle Sorte von Elementarteilchen, die man mit der Klein-Gordon-Gleichung beschreiben kann – zusammenprallen, wobei am Ende vier Pionen herauskommen. (Das geht, weil – neutrale – Pionen ihre eigenen Antiteilchen sind.1) Deshalb ist es nicht möglich, eine relativistische Gleichung aufzustellen, die nur ein einziges Teilchen beschreibt.
1Und das wiederum ist leicht einzusehen, weil sie aus einem Quark und einem Antiquark bestehen, aber das führt jetzt wirklich zu weit vom Thema ab. Vielleicht schreibe ich ja irgendwann nochmal was zum Teilchenzoo.
Stattdessen machte man den Übergang zu einer Feldtheorie, bei der die Zahl der Teilchen in der Lösung nicht konstant sein muss (wie das passiert, sehen wir noch). Diese Feldtheorie in ihrer einfachsten Form verwendet jetzt wieder die Klein-Gordon-Gleichung, diesmal aber als klassische Feldgleichung, die dann erst “quantisiert” werden muss. Das Feld φ beschreibt jetzt also keine Wellenfunktion mehr, sondern ein “klassisches” Elementarteilchenfeld. (Man kann sich vorstellen, dass φ – genauer gesagt φ2 – klassisch gesehen die Intensität (oder die Energie, das kommt aufs selbe raus) im Feld darstellt.) Den Übergang zur Quantenmechanik machen wir dann mit dem – geeignet angepassten – Pfadintegral. (Alternativ kann man auch die sogenannte “kanonische” Quantisierung verwenden – die ist aber nicht so anschaulich.)
Leider wird diese “Uminterpretation” von Wellenfunktion zu echtem Feld in vielen Büchern nicht sauber erklärt, was zumindest bei mir auch immer zu endloser Verwirrung geführt hat – deswegen habe ich das hier ja auch die “erste Verwirrung der QFT genannt”. Wenn Feldgleichungen (insbesondere die für das elektromagnetische Feld) quantenmechanisch behandelt werden, spricht man manchmal auch von “zweiter Quantisierung” – eine Bezeichnung, die ich auch immer extrem verwirrend fand, denn es klingt eben so, als würde man erst die klassische Physik quantisieren und eine Quantenmechanik mit einer Wellenfunktion haben, und die dann nochmal quantisieren, um zur Quantenfeldtheorie zu kommen. So ist es aber nicht, quantisiert wird nur einmal, aber eben ein Feld und nicht ein Teilchen. (Ja, ich weiß, ich habe noch nicht genau erklärt, wie man denn nun die Feldtheorie quantisiert und Pfadintegrale berechnet – aber die Serie ist ja auch noch nicht zu Ende.)
Wie tief ist die Dirac-See?
Diese Verwirrung ist auch verantwortlich für die Erfindung der berühmten Dirac-See, die ein Beispiel dafür ist, dass man mit fehlerhaften Konzepten trotzdem richtige Vorhersagen machen kann. (Was uns allen zur Warnung dienen soll – nur weil eine Vorhersage eintrifft, heißt das nicht, dass unsere Theorie vollkommen stimmt, selbst wenn es eine spektakuläre Vorhersage ist.)
In den Zwanziger Jahren versuchte man wie gesagt, das ψ in der Diracgleichung so zu behandeln wie die Wellenfunktion in der Quantenmechanik.
Als Dirac seine Gleichung für das Elektron aufstellte, stellte er fest, dass diese Gleichung mathematisch nur funktioniert, wenn die “Wellenfunktion” an jedem Ort nicht bloß eine Zahl ist, sondern gleich durch vier Zahlen gekennzeichnet wird. Er konnte zeigen, dass sich das letztlich mit dem “Spin” (dem Eigendrehimpuls – eine Größe, zu der ich irgendwann sicher auch mal was schreiben muss) des Elektrons in Verbindung bringen lässt. Das sprach natürlich sehr für seine Gleichung: Der Spin purzelte quasi “von selbst” aus der Gleichung heraus, ohne dass Dirac zusätzliche Annahmen machen musste. Damit konnte er gleich noch ein paar experimentelle Ergebnisse erklären, die man bisher nicht verstanden hatte. Das überzeugte Dirac davon, dass seine Gleichung nicht so ganz falsch sein könnte.
So weit, so gut. Leider gab es ein kleines Problem: Wenn man Lösungen der Gleichung berechnete, ergaben sich Wellen – das war gut. Leider gab es immer auch welche mit negativer Energie, und zwar mit beliebigen Werten – das war nicht so gut. Eigentlich müsste ein Elektron sich doch früher oder später in den Grundzustand begeben, also in den Zustand niedrigster Energie. Den gab es nur nicht, die Energien waren nach unten unbegrenzt und das Elektron müsste also unendlich viel Energie verlieren können und dabei Zustände immer niedrigerer Energie annehmen.
Das wiederum passte nicht zur Beobachtung – Elektronen im Wasserstoffatom bleiben in einem wohldefinierten Zustand und verlieren nicht immer mehr und mehr Energie.
Schade – denn die Dirac-Gleichung war erstens schön, zweitens einigermaßen einfach und machte drittens die schöne Vorhersage des Spins und einiger Experimente. Und so beschloss Dirac, nach einer Lösung des Problems zu suchen, die die Gleichung unangetastet ließ. Und genial wie er war, fand er auch ziemlich schnell eine.
Elektronen gehorchen dem berühmten Pauli-Prinzip: Es können nie zwei Elektronen im selben Zustand sein. Jeder Zustand hat also nur Platz für ein Elektron. Wenn die ganzen Zustände mit negativer Energie alle mit Elektronen besetzt wären, dann könnte ein Elektron, das irgendwo herumfliegt, nicht in diese Zustände hineingeraten, weil sie schon belegt sind, genauso wie ein Elektron in der äußeren Elektronenschale eines Kohlenstoffatoms nicht in die innere Schale hineinkann, weil dort schon zwei Elektronen sitzen. (Das habt ihr, wenn ihr einen einigermaßen brauchbaren Chemie-Unterricht hattet, vermutlich mal in der Schule gelernt.)
Dirac postulierte also eine “See” (eigentlich sollte man “Dirac sea” wohl eher mit “Dirac-Meer” übersetzen- viele schreiben auch ganz verkehrt “der Dirac-See”) aus unendlich vielen Elektronen, die die ganzen Zustände mit negativer Energie besetzt halten. Wir merken davon nichts, weil diese Elektronen überall sind (und auch überall gleich) und so einen gleichmäßigen Hintergrund bilden.
So kann man sich das bildlich vorstellen:
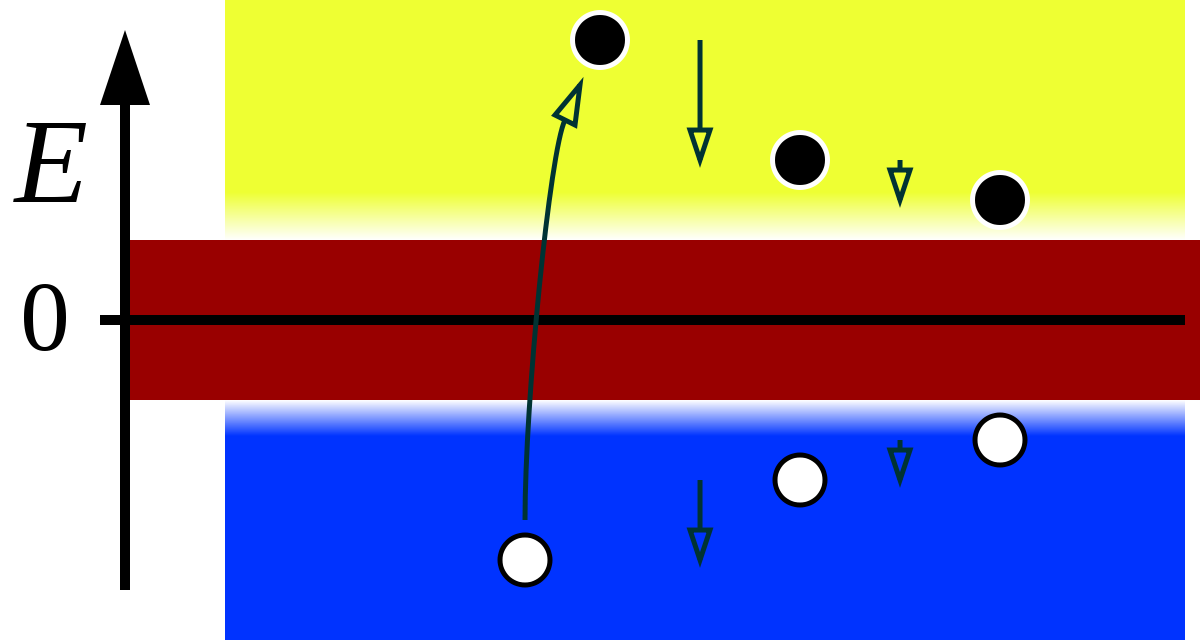
By Incnis Mrsi – Own work, Public Domain, Link
Nach oben ist hier die Energie aufgetragen. Unten in blau sind die Zustände mit negativer Energie, die (fast) alle besetzt sind.
Aus dieser Idee ergibt sich eine spannende Schlussfolgerung: Trifft man eins der Elektronen in der See (also unten im blauen Teil) mit einem Photon mit genügend hoher Energie, so würde es in einen Zustand mit positiver Energie übergehen können (Pfeil links im Bild). Man würde also ein Elektron “erzeugen” (so würde es zumindest aussehen). Da, wo das Elektron aus der See herausgeschlagen wurde, würde jetzt aber auffallen, dass ein Elektron fehlt (so wie man auch eine Luftblase im Wasser deutlich bemerkt). Diese Fehlstelle würde sich als positive elektrische Ladung bemerkbar machen (weil eben eine negative elektrische Ladung in der See fehlt) und würde sich verhalten wie ein Elektron mit positiver elektrischer Ladung. In diese Fehlstelle könnte ein anderes Elektron wieder hineinstürzen (denn sie ist ja nichts als ein unbesetzter Zustand), so dass sich Fehlstelle und Elektron gegenseitig vernichten würden. Die Energie würde dabei wieder als Photon freigesetzt.
So wurde die Idee des “Antiteilchens” geboren – ein Antiteilchen ist nach diesem Konzept eine Fehlstelle in der Diracsee. Sie benimmt sich wie ein Elektron mit einer positiven Ladung, und wenn sie auf ein Elektron trifft, dann vernichten sich beide. Wenige Jahre später wurde das Antiteilchen des Elektrons, das Positron, mit genau diesen Eigenschaften auch tatsächlich nachgewiesen. Triumph für die Dirac-See!
So findet man das Konzept in vielen Büchern erklärt. Diracs großer Triumph wird deutlich hervorgehoben. Und dann geht es weiter mit Teilchen-Antiteilchen-Paaren und (wenn man die Fachbücher liest) mit dem Formalismus der Quantenfeldtheorie, mit anderen Teilchen und so weiter. Auf die Dirac-See wird meist nicht weiter eingegangen, das Konzept hängt ein bisschen in der Luft.
Heutzutage verwendet man die Diracgleichung ja, wie bereits erklärt, anders als Dirac es tat: wir betreiben echte Quantenfeldtheorie. Die Größe ψ entspricht unserem φ, also einem “klassischen” Feld, das dann zum Beispiel mit Hilfe des Pfadintegrals (wie das genau geht, sehen wir noch) quantenmechanisch behandelt werden kann. Die Lösungen mit “negativer Energie” lassen sich dann direkt mit Anregungen des Feldes identifizieren, und zwar desjenigen Teils des Feldes, der die Antiteilchen (also die Positronen) beschreibt, und diese Antiteilchen haben auch positive Energien, so wie es sich gehört. Mit anderen Worten: Die Lösungen negativer Energie gibt es in einer echten Quantenfeldtheorie des Elektrons nicht – sie tauchen nur in der vereinfachten Dirac-Gleichungs-Variante auf, wenn man das ψ wie eine Wellenfunktion versteht.
Die wenigsten Bücher (lobenswerte Ausnahmen sind die von Weinberg und Zee) sagen explizit dazu, dass das Konzept der Diracsee längst überholt ist und heutzutage keine Bedeutung mehr hat. Wie wir gesehen haben, entstand es daraus, dass Dirac seine Gleichung als Wellengleichung für ein Teilchen, ähnlich wie die Schrödingergleichung, interpretieren wollte. In der Quantenfeldtheorie wird es nicht mehr gebraucht. Aus irgendeinem Grund steht das in den meisten Büchern nicht explizit drin – man kann es sich zwar irgendwie denken, weil das Konzept nie wieder auftaucht, aber verwirrend ist es doch.
Also: Die Dirac-See ist abgeschafft.






Kommentare (49)