QFT für alle: Von A nach B

Wenn Teilchen eigentlich nur Anregungen von Quantenfeldern sind, wieso beobachten wir dass überhaupt etwas, das man als “Teilchen” beschreiben kann? Und wie kommen diese “Teilchen” von einem Ort zum anderen? Bisher hatten wir ja nur Wellen – die waren überall gleichzeitig und passten damit nicht zu der Vorstellung, dass Teilchen irgendwo entstehen und sich ausbreiten.
In unserem Gummituch-Modell können wir uns leicht überlegen, was da passieren muss: Wir müssen das Gummituch irgendwie dazu bringen, dass sich eine Anregung (beispielsweise eine Welle) von einem Ort ausgehend ausbreitet, so wie eine Wasserwelle, wenn man einen Stein ins Wasser wirft. Wir müssen also irgendwie an unserem Gummituch zupfen.

Wie bauen wir das in unseren Feldtheorie-Formalismus ein?

(Ja, so funktioniert Physik. Man leitet nicht alles aus irgendwelchen Axiomen her, sondern man hat eine physikalische Anschauung und überlegt, wie sie sich mit dem bekannten Wissen vereinbaren lässt und wie man sie mathematisch einbaut. Dann probiert man, was herauskommt und prüft, ob es sinvoll ist und zu den Beobachtungen passt. Wenn es das nicht tut, probiert man was anderes, wenn es passt, versucht man, weitere Sachen herauszuknobeln. )

Am Gummituch zupfen heißt ja, dem Tuch eine Auslenkung aufzuzwingen, unser Feld φ ist dort also nicht Null. Und da wir in unserem Formalismus ja alles mit Hilfe der Wirkung beschreiben, müssen wir dafür sorgen, dass die Wirkung kleiner wird, wenn das Feld irgendwo nicht Null ist. Dazu fügen wir einen Ausdruck hinzu, der die Wirkung an der Stelle (und zu der Zeit), wo wir das Feld anregen wollen, entsprechend verändert. So etwas nennt man eine “Quelle”. Diese Quellen für das Feld sind auch wieder vom Ort und von der Zeit abhängig, so wie das Feld selbst. Wenn ich beispielsweise zur Zeit t am Ort x am Gummituch zupfe, dann muss ich eine Funktion definieren, die bei x und t nicht Null ist. Diese Funktion nennen wir J(x) (hier ist x wieder ein Vierervektor), und unsere Wirkung bekommt jetzt einen zusätzlichen Term, der J(x) und φ(x) enthält.

Das ist ziemlich einfach: Wir müssen einfach nur eine Quellenfunktion J(x) definieren und dann J(x)φ(x) zu unserer Lagrangefunktion hinzuzählen. Die sieht jetzt also so aus:

Dieser Ausdruck kommt jetzt ins Pfadintegral:

Dieses Integral kann man sogar lösen, weil es ein Gaußsches Integral ist – da stehen ja nur quadratische Terme im Exponenten. Dazu kann man alles diskretisieren (also das Feld nur auf einem Raumzeitgitter angucken), dann das Integral lösen und am Ende den Grenzübergang machen. Ein bisschen was dazu erkläre ich unten, Details gibt’s wie immer bei Zee.

Eine solche “Quelle” ist nichts Ungewöhnliches oder Abstraktes, sondern einfach ein “Zupfen” an unserem Gummituch. Ihr könnt euch auch vorstellen, ihr werft eine kleine schwere Kugel auf das Tuch. Dabei entsteht eine Welle, die dann an einer anderen Stelle (wo eine zweite “Quelle”, sprich Kugel, sitzt) diese zweite Kugel in die Luft schleudert, wobei die Kugel Energie aus dem Gummituch entnimmt und unsere Welle im Idealfall verschwindet.

Wenn wir statt unseres Feldes φ das elektromagnetische Feld betrachten¹ , dann ist die Quelle eine elektrische Ladung (die ja ein elektrisches Feld erzeugt) oder ein Strom, der ein magnetisches Feld erzeugt. (Denkt daran, dass Ladung und Strom eng miteinander verbunden sind, weil sie zusammen einen Vierervektor bilden, das wird eines Tages noch sehr wichtig werden.) Falls euch das immer noch begrifflich etwas unscharf vorkommt – das liegt vermutlich daran, dass ich hier mein Feld mit der QFT beschreibe, aber die Quelle nicht. Das ist vielleicht verwirrend, denn die QFT soll doch alles beschreiben können. Stimmt schon, aber wie man die Wechselwirkung zwischen zwei echten Quantenfeldern beschreibt, erkläre ich ein bisschen später. Wir können uns hier erstmal mit der Vorstellung behelfen, dass unsere Kugel so schwer oder unsere Ladung so groß ist, dass wir sie in brauchbarer Näherung mit den Mitteln der klassischen Physik beschreiben können.

¹genauer gesagt, müssten wir bei Ladungen das elektromagnetische Potential angucken, aber das ist hier nebensächlich.

Das elektromagnetische Feld ist etwas komplizierter als unser φ-Feld, weil es nicht bloß an jedem Ort eine einzige Zahl ist – elektrisches und magnetisches Feld zeigen ja jeweils in eine bestimmte Richtung – es handelt sich um ein Vektorfeld. (Falls ihr nen Auffrischungskurs zum Thema Elektromagnetismus sucht, dann… – Stimme aus dem OFF: “Wir wissen nicht, was dieser freundliche Blogger empfiehlt. Wir empfehlen bei mangelnden Elektromagnetismuskenntnissen diese Serie.” (Das war jetzt ein Scherz für die etwas ältere Generation unter den Leserinnen und Lesern.)) Das Prinzip ist aber das gleiche, und Felder, die genau so funktionieren wie unser φ-Feld hier spielen in der Physik eine wichtige Rolle. Man nennt so ein Feld wie das φ-Feld, das nur einen Wert, aber keine Richtung hat, ein Skalarfeld. (Nicht wegen der Fische, sondern weil mathematische Größen, die bloß Zahlen sind, nun mal Skalare heißen.)

Wenn wir jetzt erstmal wieder eine klassische Lösung suchen¹, dann sehen wir, dass wir die Wirkung verkleinern können, wenn φ(x) da, wo J(x) nicht Null ist, einen Wert bekommt. (Je nachdem, wie wir das machen, ist φ negativ oder positiv – wir zupfen nach unten oder nach oben.) Der darf natürlich nicht zu groß werden, denn sonst werden die anderen Beiträge (die die Änderung von φ enthalten und auch der “Extra-Term”) zur Wirkung zu groß. Wir fragen uns jetzt also, welchen Wert das Feld φ bekommt, wenn wir am Raumzeitpunkt x eine Quelle J(x) hinsetzen. Gesucht ist also φ am Raumzeitpunkt y für den Fall, dass man eine Quelle am Raumzeitpunkt x hat. Diese Größe schreibt man als D(x,y) und nennt sie den Propagator. (Nein, das ist nicht der neuste Film mit Arnold Niederegger. Aber der Propagator kommt wieder – wenn auch ohne Sonnenbrille.)

¹Ich bin hier ein bisschen schlampig – um eine Lösung zu suchen, muss man ja beim Pfadintegral einen Anfangs- und einen Endzustand festlegen. Wir können uns Zustände vorstellen, bei denen am Anfang (vor langer Zeit) reines Vakuum herrschte, am Ende (in ferner Zukunft) wieder nur Vakuum da ist und wir uns fragen, was dazwischen passiert, wenn wir Quellen anschalten. Weiter unten bin ich etwas genauer.

So etwas Ähnliches haben wir schon beim Pfadintegral gemacht: Da hatten wir eine Elektronenquelle bei Q und haben die Amplitude dafür gesucht, dass das Elektron bei x ankommt. Hier ist das jetzt ganz analog, nur dass jetzt der Ort der Quelle x heißt und der, an dem wir gucken, y, und dazwischen haben wir nicht bloß ein Elektron, sondern ein ganzes Feld.

Wenn euch der Propagator nicht anschaulich genug ist, dann denkt an ein einfaches Alltagsbeispiel: Ihr steht an einem schönen Teich mit ruhigen Wasser (es funktioniert übrigens auch genauso mit unserem Gummituch). Jetzt werft ihr einen Stein ins Wasser: Am Ort x zur Zeit t (also am Raumzeitpunkt x) wird die Wasseroberfläche durch den Stein ausgelenkt und es entsteht eine Welle. In der Realität sind es meist mehrere Wellenberge und -täler, die entstehen, das liegt vor allem daran, dass der Stein ja die Oberfläche eine gewisse Zeit lang stört. Jetzt fragt ihr euch: Wenn ich bei x den Stein ins Wasser werfe, wie hoch ist dann der Wasserstand bei einer anderen Zeit an einem anderen Ort, also am Raumzeitpunkt y. Es ist klar, dass das Wasser nun dann nennenswert aus der Ruhelage ausgelenkt ist, wenn die Wasserwelle diesen Punkt gut erreichen kann. Breitet sich die Wasserwelle mit einer Geschwindigkeit v aus, dann muss der räumliche Abstand gerade gleich vt sein, wenn t der zeitliche Abstand ist. Außerdem gilt: Je weiter ihr vom Ursprung weg seid, desto weniger stark ist die Auslenkung (weil sich die Welle kreisförmig ausbreitet und der Umfang ja immer größer wird). Die Auslenkung am Raumzeitpunkt y, wenn eine Quelle (mit festgelegter Stärke) am Raumzeitpunkt x aktiv war, nennt ihr D(x,y).

Wenn ihr diese Serie extrem aufmerksam gelesen habt (und das habt ihr doch alle?), dann fällt euch vielleicht auf, dass wir dieses Gebilde schon kennen. Als wir klassische Felder diskutiert haben, da habe ich euch diese Animation gezeigt:

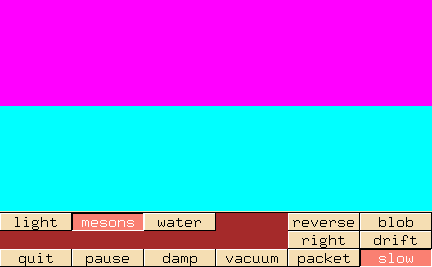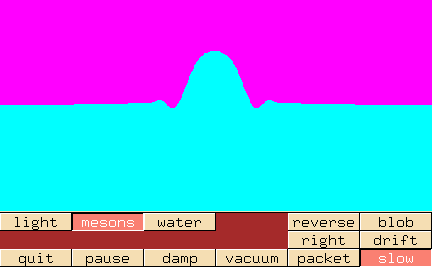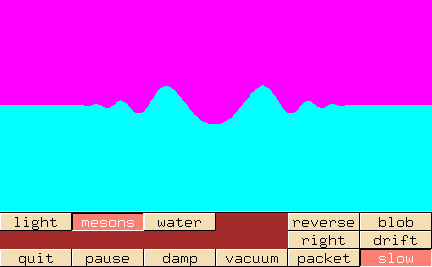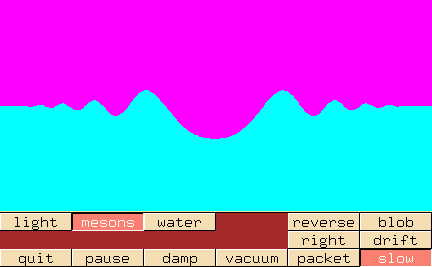
Sie zeigt genau das, was ich hier noch einmal erklärt habe: Wie sich das Feld von einer Anregung (in unserem neuen Fachjargon “Quelle” genannt) ausbreitet.

Wir können uns den Propagator auch anders anschaulich machen, nämlich indem wir ihn in ein Raumzeit-Diagramm eintragen. Stellt euch vor, ihr würdet die Einzelbilder aus der Animation alle hintereinander hängen, so dass ein dreidimensionales Gebilde entsteht. Und dann schaut ihr von oben drauf. Das sieht dann so aus:

By Cyp – Own work, CC BY-SA 3.0, Link

In der Mitte ist der Punkt, wo die Quelle sitzt (und das ist hier ein Raumzeitpunkt, die Quelle ist also nur für einen unendlich kurzen Moment da). Nach oben ist die Zeitrichtung aufgetragen, horizontal die Raumrichtung. Eine diagonale Linie unter 45° entspricht wieder einem Lichtstrahl (man nennt das auch den Lichtkegel). Wie ihr seht, ist der Wert von φ auf dem Lichtkegel halbwegs groß. Ein Teil der Störung breitet sich also mit Lichtgeschwindigkeit aus, denn für alle Punkte auf dem Lichtkegel gilt, dass ihr räumlicher Abstand zum Ursprungspunkt genau gleich ct ist – erinnert ihr euch noch an den Anfang dieser Serie?

Wenn ihr am Ort der Quelle (also auf einer senkrechten Linie in der Mitte) guckt, dann seht ihr dort helle und dunkle Streifen – ein Vergleich mit der Animation oben zeigt, dass die dem Auf- und Abschwingen des Feldes entsprechen. (Quantitativ passen die beiden Bilder nicht perfekt zusammen, nicht, dass sich jemand wundert.)

Hier dasselbe Bild, aber mit einem kleineren Wert für unseren “Extra-Term” m:

By Cyp – Own work, CC BY-SA 3.0, Link

Ihr seht also, dass es von unserem “Extra-Term” (Parameter m) abhängt, wie stark der Propagator vom Lichtkegel abweichen darf. Das spricht schon dafür, dass dieser Extra-Term etwas mit der Masse zu tun hat – wenn man ihn gegen Null gehen lässt, ist die Störung ziemlich eng auf dem Lichtkegel konzentriert¹, wenn der Term groß ist, dann bleibt die Störung länger am Ort.

¹Verwirrenderweise darf sie aber leicht vom Lichtkegel abweichen. Für Quantenteilchen gelten auch die Regeln der SRT nur mit gewissen Einschränkungen – ein Photon hat auch eine Amplitude dafür, sich schneller oder langsamer als Lichtgeschwindigkeit fortzubewegen, so seltsam das klingen mag. Erst im Mittel kommt die Lichtgeschwindigkeit heraus. Und nein – auch das verletzt nicht die Spezielle Relativitätstheorie.

Im Bild seht ihr noch etwas Merkwürdiges: Die Zeit läuft ja von unten nach oben. Es sieht so aus, als ob sich die Lösung im Bild auch in die Vergangenheit ausbreitet. Das versteht man am leichtesten an unserem Teichbeispiel: Es könnte ja theoretisch sein, dass eine kreisförmige Welle von außen auf einen Punkt zuläuft und diesen genau in dem Moment erreicht, wo der Stein ins Wasser fliegt, so dass sich die einlaufende Welle und die, die der Stein erzeugt, gegenseitig aufheben und ruhiges Wasser übrigbleibt. Das ist natürlich in der Realität beliebig unwahrscheinlich, aber nicht unmöglich. Dieser Teil des Propagators wird deswegen normalerweise nicht betrachtet, weil das zwar mathematisch funktioniert, physikalisch aber nicht.

Die klassische Klein-Gordon-Gleichung bekommt jetzt eine rechte Seite

Die Lösungen davon sind (wenn J eine punktförmige Anregung ist, also mathematisch gesehen eine δ-Funktion¹) die berühmten Greensfunktionen. Genauer gesagt gilt: Ist φ(y) eine Lösung für die Gleichung mit J(x)=δ(x), ist die Greensfunktion D(x,y)=φ(y).

¹ Ja ich weiß, mathematisch korrekt heißt das δ-Distribution, aber so pingelig ist hier hoffentlich keiner.

Je nachdem, welche Lösung man sucht (die in die Vergangenheit oder Zukunft) kann man die avancierte oder retardierte Greensfunktion verwenden.

Denkt noch einmal an unser Teichbeispiel. Wir nehmen einen sehr großen Teich und ich schmeiße einen Stein jetzt und hier hinein und schaue, wie groß die Wasserwelle zwei Sekunden später in einem Abstand von 70 Zentimetern ist. Dann wiederhole ich das Experiment zu einem späteren Zeitpunkt und schmeiße den Stein an einem anderen Ort ins Wasser. Wieder messe ich die Wasserwelle zwei Sekunden später in einem Abstand von 70 Zentimetern. Es wird hoffentlich niemanden überraschen, dass das Ergebnis dasselbe ist. Für den Propagator kommt es also nur auf die Differenz zwischen “Quelle bei x” und “gemessen bei y” an, also auf (x-y).

Da unser Universum (von Dingen wie der Expansion und ähnlichen extrem langsamen und großmaßstäblichen Phänomenen abgesehen) überall und zu jeder Zeit gleich aussieht, gilt hier dasselbe. Wir können den Propagator also schreiben als D(x-y).

Ausgestattet mit unserem Propagator werfen wir jetzt einmal einen ersten Blick darauf was passiert, wenn wir zwei Quellen haben. Unsere Quellenfunktion J ist jetzt an zwei Raumzeitpunkten von Null verschieden, einmal bei einem Punkt x, einmal bei einem anderen Punkt y. Können diese miteinander in Wechselwirkung treten, indem sie unser φ-Feld beeinflussen?

Intuitiv sollte man erwarten, dass die beiden sich dann deutlich beeinflussen, wenn der Propagator der einen Quelle am Ort der anderen Quelle nicht verschwindet – genau wie wir uns das oben für die Wasserwelle überlegt haben:

Modifiziertes Bild, Quelle:  Cyp – Own work, CC BY-SA 3.0, Link

Hier habe ich drei Quellen gezeichnet. Von der Quelle bei x geht der Propagator aus (hier haben wir am Gummituch geruckelt oder einen Stein ins Wasser geworfen). Die dadurch hervorgerufene Veränderung des Feldes breitet sich jetzt aus. Am Punkt y₁ sitzt eine passende Quelle (eigentlich sollte man “Senke” sagen, weil die ja die Störung aufnimmt, diesen Unterschied macht man aber nicht, genau wie in der Physik Bremsen auch eine Beschleunigung ist). Die Quelle am Punkt y₂ dagegen wird vom Propagator kaum “getroffen”, deswegen ist der zugehörige Term klein. Natürlich kann vom Punkt y₂ wieder eine Welle ausgehen (dort ist ja auch eine Quelle), aber diese beiden Wellen würden sich eben nicht “sehen” und hätten nichts miteinander zu tun. Stellt euch wieder das Gummituch vor: Bei x habt ihr eine Kugel draufgeworfen, und dann werft ihr bei y₁ wieder eine Kugel drauf, die jetzt aber vielleicht genau in dem Moment ankommt, als das Tuch gerade eine Welle nach oben schlägt. Die Welle, die die zweite Kugel erzeugen würde und die, die gerade ankommt, überlagern sich und löschen sich im Extremfall aus – dabei verschwindet die Energie aber nicht, sondern wird auf die Kugel übertragen.

Das ist alles anschaulich einigermaßen klar und sollte besser auch in unserem Formalismus herauskommen, sonst ist alles, was wir uns überlegt haben, für die Tonne. Wie kitzeln wir jetzt so ein Ergebnis aus unserem Pfadintegralformalismus heraus?

Mit dem Pfadintegral können wir ja immer nur Amplituden berechnen – wie ist die Amplitude dafür, dass aus einem bestimmten Anfangszustand ein bestimmter Endzustand wird? Wir brauchen jetzt eine geschickte Wahl des Anfangs- und Endzustands, mit der wir herausbekommen können, welchen Einfluss unsere Quellen haben und ob unsere Intuition von eben auch stimmt.

Unsere Quellen sind ja nur für jeweils einen Moment (an den Raumzeitpunkten x und y) da (später betrachten wir auch Quellen, die länger aktiv sind). Ich nehme hier der Einfachheit halber an, dann x zeitlich vor y liegt, so wie im Bild oben. (Das ist in keiner Weise zentral und macht nur die Sprechweise einfacher – Mathematiker sagen dazu oBdA “Ohne Beschränkung der Allgemeinheit”.) Lange vor x, in ferner, ferner Vergangenheit, ist von den Quellen natürlich nichts zu merken – wir haben ein Vakuum. Dann sind unsere Quellen aktiv (erst x, dann y), tun irgendetwas mit unserem Feld, und dann passiert nichts mehr. Wir haben also in ferner Vergangenheit und in ferner Zukunft jeweils einen Vakuumzustand.

Da gibt es leider eine kleine Komplikation, mit der wir uns im Moment nicht herumschlagen wollen (kommt hoffentlich irgendwann später – je nachdem, wann mir in dieser Serie die Luft ausgeht, die mal wieder “etwas” länger wird als gedacht). Unsere Quellen befinden sich im Vakuum – aber das Vakuum ist in der QFT auch schon ein ziemlich kompliziertes Gebilde (vermutlich habt ihr schon mal von den “Vakuumfluktuationen” oder den “virtuellen Teilchen im Vakuum” gehört). Diese Komplikation möchte ich uns erstmal gern ersparen. Wir machen deshalb folgendes: Wir vergleichen die Situation mit Quellen mit der Situation ohne Quellen. Dann heben sich die ganzen nervigen Vakuumfluktuationen weg.

Wir berechnen also die Amplitude dafür, dass ein Vakuum in ferner Vergangenheit in ein Vakuum in ferner Zukunft übergeht. Um den Einfluss der Vakuumfluktuationen loszuwerden, tun wir das zweimal: Einmal mit Quellen, und einmal ohne. Wenn wir diese beiden Amplituden miteinander vergleichen, dann sehen wir direkt den Einfluss der Quellen auf die Amplitude.

Mathematisch bedeutet das einfach, dass wir am Ende alle Ausdrücke, die kein J enthalten, ignorieren.

Wir berechnen also wieder ein Pfadintegral (das wie gesagt mit Pfaden nicht viel zu tun hat, sondern eigentlich Feldkonfigurationsintegral heißen sollte), aber diesmal eins mit eingebauten Quelltermen J. Und diesmal rechnen wir das auch wirklich aus (jedenfalls im bösen Formelteil).

Das geht hier genauso wie in der Quantenmechanik: Dort haben wir für jeden denkbaren Pfad die Wirkung berechnet. Zu jedem Pfad gehört ein Amplitudenpfeil, die haben wir alle addiert und das Ergebnis war die Gesamtamplitude.

Statt Pfaden haben wir jetzt Konfigurationen, wir müssen also für jede denkbare Feldkonfiguration die Wirkung berechnen, daraus den zugehörigen Amplitudenpfeil, und alle diese Pfeile addieren wir dann
auf. Ich schreibe die Formel hier ruhig mal hin – wenn ihr sie mit den Formeln aus dem Pfadintegral für ein einzelnes Elektron vergleicht, dann seht ihr, dass das gar nicht so schlimm ist. Ich nenne die Amplitude jetzt Z, weil das der übliche Buchstabe ist. Z(J) schreibe ich, weil das Z ja von unseren Quellen J abhängt:

Da wo beim Elektron über alle Wege summiert wird, summieren wir jetzt über alle Feldkonfigurationen φ, und an der e-Funktion steht wieder der Drehwinkel: Die Wirkung S in Einheiten von ħ. S hängt dabei natürlich vom Feld φ ab, jetzt aber zusätzlich auch vom Quellterm J.

Die kurze Rechnung klaue ich im Buch von Zee:

Jetzt wird partiell integriert (wobei man an den Grenzen ein bisschen rumargumentieren muss…), und man bekommt

In der Klammer seht ihr quasi schon die Klein-Gordon-Gleichung. Das ist jetzt letztlich ein Gaußsches Integral, das man (mit Hilfe des Propagators und ein bisschen Rechnerei) lösen kann. Es ergibt sich (für den allgemeinen Fall beliebiger J’s):

Dabei enthält Z(0) genau die Terme ohne J, also den ganzen Vakuumkram. (In dieser Rechnung habe ich mir das ħ wieder gespart, das gehört im Exponenten natürlich rein.)

Der mathematische Formalismus macht es dabei sehr leicht, den Anteil der Amplitude, der zu reinen Vakuumfluktuationen gehört, von dem zu trennen, der etwas mit den Quelltermen zu tun hat. Das Ergebnis für den interessanten Teil enthält einen einfachen Ausdruck. Der Drehwinkel für die Amplitude ändert sich mit unseren zwei Quellen am Raumzeitpunkt x und y genau um den Wert
-J(x) D(x-y) J(y)/2.

Was bedeutet das? J(x) ist der Wert der Quelle am Raumzeitpunkt x, J(y) der am Punkt y, und dazwischen steht der Propagator. Dieser Ausdruck kann nur einigermaßen groß sein, wenn J(x) und J(y) beide einen Wert haben und wenn der Raumzeitabstand von x und y gerade so ist, dass der Propagator von x nach y auch hinreichend groß ist. Das ist genau das, was wir uns oben anschaulich mit dem Bild des Propagators überlegt haben.

Auch hier wird wieder über alle diese Terme summiert.

Man kann dasselbe auch mit Hilfe des Operatorformalismus und der Zeitordnung mit dem Wick-Theorem ausrechnen (so steht es auch in den meisten Büchern drin). Das ist in meinen Augen wesentlich unanschaulicher, weil das Ergebnis aus der Fouriertransformation der Heaviside-Funktion herauspurzelt. Wenn jemand eine gute Anschauung für diese Rechnung hat, dann immer her damit.

Das Ergebnis ist also ganz logisch: Es gibt eine Wechselwirkung zwischen zwei Quellen, wenn das Signal von der einen die andere erreichen kann. Warum dieses Signal ein “Teilchen” ist und was es mit dem berühmten Unterschied zwischen “virtuellen” und “realen” Teilchen auf sich hat (den es in Wahrheit gar nicht gibt), das klären wir im nächsten Teil. Und dann müssen wir noch klären, wie sich so eine Wechselwirkung eigentlich bemerkbar machen würde. Kann man so etwas messen?

---

Einen Überblick über die ganze Serie findet ihr übrigens hier.