Das Versteck in der Zeit

Unsichtbarkeit ist ja schon eine feine Sache. Genauso praktisch wäre es natürlich, wenn euer Erzrivale und Fernschachgegner glaubt, er würde euch lückenlos überwachen, während ihr in Wahrheit ganz woanders seid. Ein solches Phänomen wurde vor kurzem technisch realisiert – jedenfalls in sehr kleinem Maßstab.

Das ganze verwendet ziemlich raffinierte Tricks aus der modernen Optik (von denen ich bisher auch noch nie gehört hatte). Ich erkläre es erst einmal mit einer Analogie, die aus dem Begleitartikel in nature stammt:

Stellt euch vor, ihr wolltet herausfinden, ob auf einer Straße irgendwo eine Baustelle ist. Ihr könnt den Ort der Baustelle (wenn denn eine da ist) selbst nicht sehen, wohl aber den Bereich davor und dahinter. Vor der Baustelle fahren die Autos alle in gleichmäßigem und konstantem Tempo. An der Baustelle gibt es – na klar – einen Stau und die Autos werden langsamer. Entsprechend beobachtet ihr – wenn eine Baustelle da ist – dass der Autostrom unterwegs irgendwo verzögert wird.

Wenn jemand die Baustelle vor euch verbergen will, dann könnte er den Autostrom einfach umleiten – beispielsweise auf eine Umgehungsstraße. Das entspricht der “Unsichtbarkeit”. Eine andere Möglichkeit besteht darin, die Autos hinter der Baustelle hinreichend zu beschleunigen – vor der Baustelle bremsen sie etwas ab, hinterher beschleunigen sie und fahren kurzzeitig schneller als mit ihrer normalen Geschwindigkeit und holen so die Verzögerung wieder auf. Das ist so etwa das Prinzip des Zeitverstecks (im Englischen “time cloak” genannt).¹

¹Fans von Perry fühlen sich vielleicht beim Begriff “Zeitversteck” an das Antitemporale Gezeitenfeld erinnert, aber das funktioniert ganz anders.

Wie gesagt, beim “time cloak” arbeitet man natürlich nicht mit Autos, sondern mit Licht. Der zu beobachtende Bereich wird kontinuierlich mit Licht bestrahlt und am anderen Ende kommt auch ein kontinuierlicher Lichtstrahl an. Trotzdem wird das Licht unterwegs “unterbrochen” und es entsteht eine “Lücke” im Lichtstrahl, die wieder geschlossen wird.

Damit das klappt, muss man drei Dinge tun: Man muss den kontinuierlichen Lichtstrahl irgendwie an einer Stelle “unterbrechen”. Dann muss man den vorderen Teil des Strahls beschleunigen, den hinteren abbremsen. So entsteht eine “Lücke” im Strahl, in der wir unsere raffinierten Pläne vor dem beobachtenden Erzrivalen (und Fernschachgegner) verbergen können. Hinterher muss man den hinteren Teil des Strahls wieder beschleunigen und den vorderen abbremsen, so dass wieder ein lückenloser Gesamtstrahl entsteht.

Aber hat Licht nicht immer dieselbe Geschwindigkeit? Heißt es nicht ständig und allerorten, dass die Lichtgeschwindigkeit konstant ist?

Stimmt schon, aber das gilt nur für die Vakuum-Lichtgeschwindigkeit. In einem optischen Medium (Physikersprech für “durchsichtiges Zeugs”) ist die Lichtgeschwindigkeit kleiner als im Vakuum. Dass das zur Lichtbrechung führt, habe ich vor ein paar Monaten im Zusammenhang mit der Unsichtbarkeit am Beispiel des Rettungsschwimmers David H. schon erklärt.

Für uns hier ist wichtig, dass die Lichtgeschwindigkeit in einem optischen Medium nicht nur kleiner ist als im Vakuum, sondern vor allem, dass ihre Geschwindigkeit von der Wellenlänge abhängt. Meistens ist sie um so kleiner, je kleiner die Wellenlänge der Welle ist, aber das ist nicht zwingend so und es gibt auch Medien, in denen es genau umgekehrt ist. Wenn die Lichtgeschwindigkeit von der Wellenlänge abhängt, spricht man übrigens auch von Dispersion.

Licht unterschiedlicher Wellenlängen bewegt sich also durch Glas unterschiedlich schnell. Fangen wir mit Licht einer bestimmten Wellenlänge an, dann können wir eine Lücke im Wellenzug erzeugen, wenn wir lokal an einer Stelle die Wellenlänge ändern, nämlich so, dass sie vorn im Lichtstrahl kürzer wird und hinten länger. (Wie man das macht, diskutieren wir gleich.) Den Übergang zwischen den Wellenlängen machen wir dabei hübsch graduell. Dieses Bild hier (aus dem Nature-Begleitartikel) zeigt das Prinzip:

Dann schicken wir das Licht durch ein optisches Medium (eine Glasfaser), in dem die vordere (kurzwellige) Hälfte schneller läuft als die hintere (langwellige). So entsteht eine Lücke im Lichtstrahl (die Pfeile veranschaulichen, wie die Trennlinie zwischen langer und kurzer Wellenlänge auseinanderläuft):

In dieser Lücke plazieren wir jetzt unser zu versteckendes Ereignis. Anschließend durchläuft der Lichtstrahl wieder eine Glasfaser, die aber diesmal das umgekehrte Geschwindigkeitsverhältnis hat, so dass jetzt der vordere Teil gebremst und der hintere beschleunigt wird. Ist die Lücke wieder geschlossen, verschieben wir die Wellenlängen wieder passend so, dass eine ungestörte Welle entsteht:

Soweit das Prinzip. Die echte Kniffligkeit besteht natürlich vor allem darin, ein Lichtsignal passend aufzuspalten. Dazu nutzt man ein Gerät, das als “Zeitlinse” bezeichnet wird (genauer gesagt verwendet man halbierte Zeitlinsen, aber bevor ich das erkläre, kommt erst mal die ganze Zeitlinse). Da ich nicht so den Durchblick in Sachen Optik habe, sind die folgenden Erklärungen vermutlich etwas ungenau – wenn jemand von euch mehr Ahnung von Optik hat, tobt euch in den Kommentaren aus und ich korrigiere das hier entsprechend.

So wie normale Linsen Licht im Raum bündeln, bündeln Zeitlinsen Licht in der Zeit. Eine Linse fokussiert ja Lichtstrahlen auf einen Punkt im Raum (Bild von Wikipedia):

Von derivative work: Mouagip (talk) Sammellinse.png: Michael Schreiter Diese Vektorgrafik wurde mit dem Adobe Illustrator erstellt. – Sammellinse.png, CC BY-SA 3.0, Link

Damit kann man dann – das habt ihr sicher mal in der Schule gelernt – Lupen, Teleskope und Mikroskope bauen.

Eine Zeitlinse tut etwas Ähnliches. Sie “bündelt” einen Impuls in der Zeit – ein Lichtimpuls kann mit ihr zu einem kürzeren Impuls zusammengestaucht werden. Schematisch kann man das so zeichnen:

Dabei habe ich den Lichtimpuls als einfachen “Berg” gezeichnet. In Wahrheit besteht Licht aber ja aus Wellen – oder, anders gesagt, man kann jeden Lichtimpuls als Überlagerung von vielen Wellen darstellen. Das ist der Trick mit der Fourier-Transformation, den ich neulich in ganz anderem Zusammenhang schon mal erklärt habe.

Im Wellenbild bedeutet ein Zusammenstauchen des Impulses, dass wir mehr unterschiedliche Wellenlängen in das Lichtsignal einbauen müssen. Eine Zeitlinse modifiziert also einen Lichtimpuls, indem Anteile von Lichtwellen mit unterschiedlicher Wellenlänge hinzugefügt werden.

Wie ganz genau so eine “Zeitlinse” technisch funktioniert, habe ich nicht herausbekommen können – anscheinend schickt man das Lichtsignal in einen Wellenleiter (also einen leitenden Kanal), der aus Silizium gefertigt ist und einen Querschnitt von ein paar Hundert Nanometern hat (siehe z.B. hier). Die Mathematik dahinter ist auch nicht so ganz ohne…

Was wir hier brauchen, ist eine “halbierte Zeitlinse” (auch da muss ich leider passen, was die technischen Details angeht). Sie verschiebt die Frequenz eines Signals ebenfalls, aber fügt nur entweder kürzere oder längere Wellenlängen hinzu. Aus einem Signal mit konstanter Wellenlänge wird ein sogenanntes “Chirp”-Signal (chirp=”tschilp”). Hier ein Bild von Wikipedia, das mehr sagt als tausend Worte:

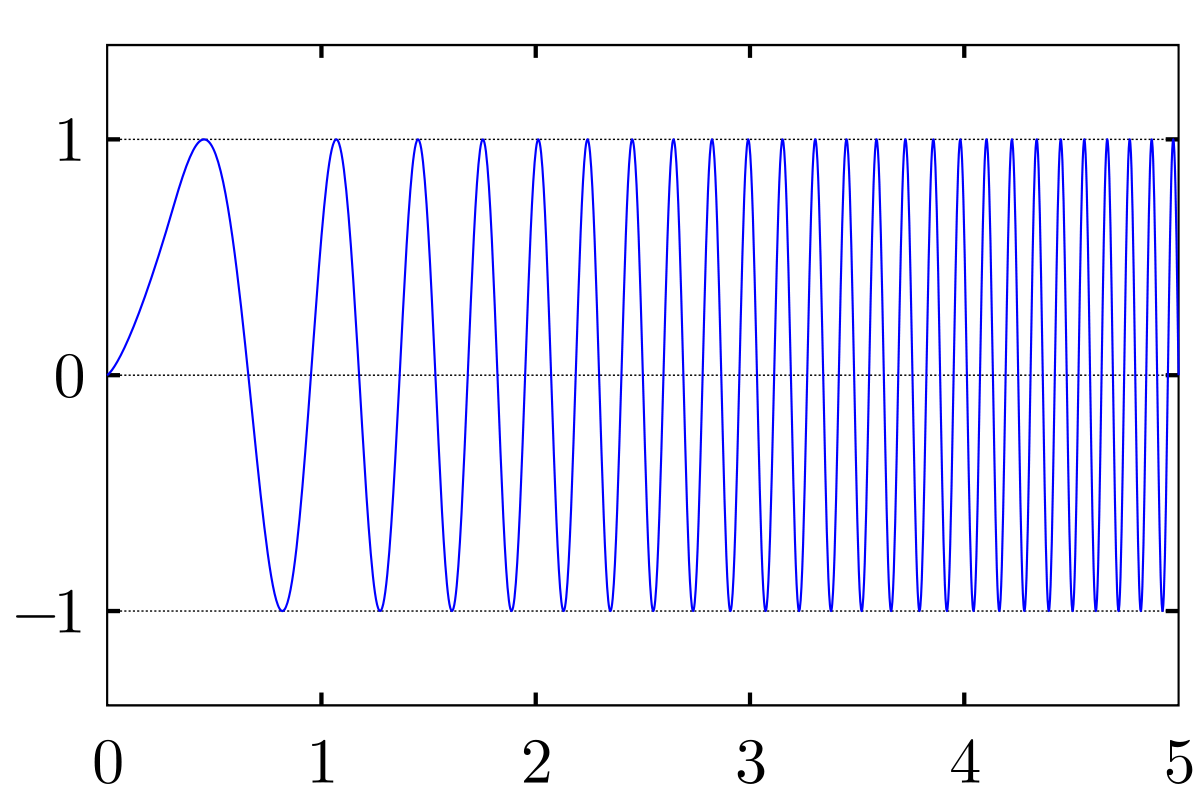
Von Georg-Johann – Eigenes Werk, CC BY-SA 3.0, Link

Rechts im Bild ist die Frequenz hoch, dann wird sie kontrolliert niedriger (die Wellenlänge nimmt entsprechend zu).

Wir verwenden zwei solche “halbierte” Zeitlinsen, eine, die einen Teil des Signals kontrolliert zu längeren Wellenlängen verschiebt, eine, die das in Richtung kürzere Wellenlängen tut. Damit wird dann das zuvor gleichmäßig grüne Licht so verschoben, wie es oben im Teilbild b und f zu sehen ist. Der Rest ist dann “einfach” – wir brauchen nur die Glasfasern mit der passenden Dispersion.

Hier nochmal eine etwas andere Darstellung direkt aus der Veröffentlichung:

Oben seht ihr nochmal den Aufbau selbst – die Schleifchen stellen die Glasfaser dar, die Zahl (in Einheiten ps/nm) gibt die Stärke der Dispersion – also der Wellenlängenabhängigkeit der Lichtgeschwindigkeit – an und ist links und rechts des zu verbergenden Ereignisses genau entgegengesetzt. In der unteren Bildhälfte seht ihr die Frequenzdarstellung des Signals, die zeigt, wie es durch die halbierten Zeitlinsen aufgespalten wird und dann durch die unterschiedlichen Geschwindigkeiten die Lücke entsteht und am Ende wieder zusammengefügt wird.

Um Nachzuweisen, dass der Effekt auch tatsächlich funktioniert, haben die Forscher allerdings kein unbeobachtetes Verbrechen begangen (das wäre bei einer “Zeitlücke” von sagenhaften 50 Picosekunden – 0.00000000005 Sekunden – auch ziemlich schwierig), sondern sie haben in der “Zeitlücke” einen Lichtimpuls erzeugt, der mit dem grünen Lichtstrahl gewechselwirkt (oder heißt das wechselgewirkt?) hätte.

So sieht das im Experiment aus:

Die blau gestrichelte Kurve zeigt, was man sieht, wenn das “Zeitversteck” ausgeschaltet ist – alle 24 Mikrosekunden gibt es ein klares Signal des Lichtimpulses, überlagert von ziemlich viel Rauschen. Mit eingeschaltetem “Zeitversteck” sieht man dagegen nur noch das Rauschen, von den Pulsen bleibt nicht mehr viel zu sehen.

O.k., ich geb’s zu – wenn Professor F. euch nicht gerade mit monochromatischem Licht beobachtet und wenn eure geheimen Pläne länger brauchen als ein paar Picosekunden, dann ist die Zeit-Tarnkappe nicht besonders nützlich. Wie groß kann man so eine Zeit-Tarnkappe denn machen?

Das hängt von der Größe des Gesamtsystems (also vor allem der Glasfasern) ab. Die Zeitlücke kann nicht länger sein als die Zeit, die ein einzelnes Lichtsignal braucht, um das gesamte System zu durchqueren. Da die Lichtgeschwindigkeit auch in Glasfaserkabeln ziemlich hoch ist, braucht ihr für eine Zeitlücke von einer Sekunde also ein Glasfaserkabel von ein paar Hunderttausend Kilometern Länge. (Oder ihr braucht langsames Glas wie in der SF-Geschichte “Light of other days” von Bob Shaw.)

Auch wenn die Zeit-Tarnkappe keine direkte praktische Anwendung hat, ist sie eine praktische Demonstration, wie man Lichtsignale manipulieren kann. Falls unsere Computer eines Tages von elektronischer auf optische Datenverarbeitung umgestellt werden, werden solche Techniken vermutlich nützlich sein. Und konzeptionell ist die Zeit-Tarnkappe auf jeden Fall spannend.

Der Artikel selbst ist in nature erschienen:
Fridman, M., Farsi, A., Okawachi, Y., & Gaeta, A. (2012). Demonstration of temporal cloaking Nature, 481 (7379), 62-65 DOI: 10.1038/nature10695

Das erste Bild von oben stammt aus dem zugehörigen Begleitartikel, der die Sache auch noch mal erklärt:
Robert W. Boyd, Zhimin Shi
“How to hide in time”
Nature, 5.1.2012, p. 35

Eine ausführliche und sehr gute Erklärung findet man auch im Blog Skulls in the Stars