Es war einmal, vor langer Zeit, in einem ganz ganz nah gelegenen Blog…
Die Leser, die ihr Wissen aus einem geheimen Blog beziehen, haben einen ersten Sieg gegen den bösen Formalismus der Quantenfeldtheorie errungen.
Dabei ist es einigen der Leser gelungen, Geheimformeln über das entscheidende Element der Quantenfeldtheorie in ihren Besitz zu bringen, den PROPAGATOR, dessen Formelmacht ausreicht, um viele physikalische Phänomene zu verstehen.
Verfolgt von den finsteren Kräften mathematischer Verwirrung haut Blogautor Martin in die Tasten, als Hüter der anschaulichen Erklärungen, die seinen Leser das physikalische Verständnis wiederbringen könnten…
Nach diesem etwas überzogenen Vorspann geht es heute um Kräfte – deswegen auch der Titel des Textes. Es ist ja schon eine Weile her, dass wir uns den Propagator angesehen haben. Dabei haben wir als Beispiel zwei Quellen betrachtet, die irgendwo in der Raumzeit sitzen und unser Quantenfeld beinflussen können.
Die Quellen waren J(x) und J(y), wobei x und y jeweils zwei Raumzeitpunkte waren. Anschaulich haben wir uns vorgestellt, unser Quantenfeld wäre die Oberfläche eines Teichs, in den wir Steine hineinwerfen.
Betrachten wir ein reines Vakuum, also den Fall ganz ohne Quellen, dann gibt es eine Wahrscheinlichkeitsamplitude dafür, dass das Vakuum am Anfang (vor langer, langer Zeit) in eins am Ende (in ferner Zukunft) übergeht – die Wahrscheinlichkeit ist natürlich gleich 1 (aus Vakuum wird Vakuum), aber der Amplitudenpfeil, den wir ja immer zeichnen, um einen Prozess zu beschreiben, zeigt in eine bestimmte Richtung.
Die beiden Quellen sorgen dabei für eine Änderung der Wahrscheinlichkeitsamplitude, sie drehen den Amplitudenpfeil also um einen zusätzlichen Betrag. (Man könnte annehmen, dass sie auch dafür sorgen könnten, dass aus dem Vakuum am Ende kein Vakuum mehr wirkt – wenn es Quellen sind, könnten sie ja vielleicht auch “echte” Teilchen erzeugen – aber wenn man die Quellen hinreichend vorsichtig an- und ausschaltet, dann kann das nicht passieren.)
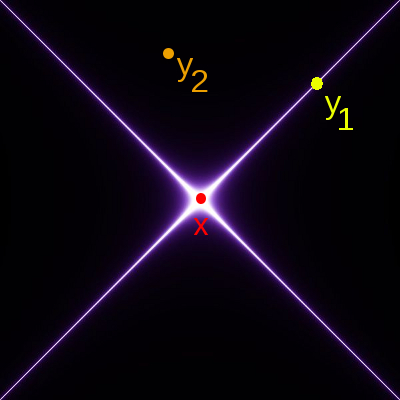
Die zusätzliche Drehung des Amplitudenpfeils hat den Wert -J(x) D(x-y) J(y)/2. Dabei ist J(x) die Stärke der Quelle am Raumzeitpunkt x, J(y) entsprechend für den Raumzeitpunkt y, und D(x-y) ist der Propagator. Dieses schon mehrfach gezeigte Bild sollte veranschaulichen, wie die beiden Punkte wechselwirken:
Nach einer Vorlage von Cyp – Own work, CC BY-SA 3.0, Link
Anschließend habe ich mich dann über den Unterschied zwischen “virtuellen” und “realen” Teilchen ausgelassen (den es in Wahrheit streng genommen gar nicht gibt). Aber wie können wir die zusätzliche Rotation der Amplitude interpretieren? Was bedeutet sie? Das wollen wir jetzt klären.
Damit ich im folgenden diese “Extradrehung” leichter hinschreiben kann, gebe ich ihr ein neues Formelzeichen: W(J). Das Argument J brauchen wir deswegen, weil der Wert der Extradrehung natürlich davon abhängt, wo unsere Quellen sitzen und wie stark sie sind.
Dazu betrachten wir ein Gedankenexperiment. Wir stellen uns zwei Orte “hier” (bei x) und “da” (bei y) vor (der Fettdruck soll darauf aufmerksam machen, dass das jetzt keine Raumzeitpunkte (Vierervektoren) sind, sondern wirklich feste Raumpunkte (ausgewählt in einem bestimmten Bezugssystem)). Wir haben dann zwei Quellen, eine “hier” und eine “da”.
Damit wir einen sinnvollen Anfangs- und Endzustand haben, mit dem wir leicht umgehen können (denn wir berechnen am Ende ja immer noch ein Pfadintegral, das uns die Amplitude dafür gibt, dass aus einem Zustand ein anderer wird), stellen wir uns vor, dass wir die Quellen mit einem Schalter versehen. Vor langer langer Zeit sind beide Quellen nicht aktiv (wir haben ein Vakuum), dann drehen wir sie (langsam, aber nicht zu langsam) auf, bis sie ihre volle Stärke J(x) und J(y) erreichen. Wir lassen die Quellen für lange Zeit aktiv (und zwar für viel länger, als wir zum Aufdrehen der Quellen gebraucht haben), dann regeln wir sie in ferner Zukunft wieder herunter, so dass unser Universum wieder ein Vakuum ist.
Wenn wir das so machen, dann können wir davon ausgehen, dass der genaue Mechanismus des Aufdrehens und Runterregelns egal ist, weil die Zeit dazwischen sehr lang ist (wir werden am Ende sehen, dass W(J) vom Zeitintervall abhängt, für das die Quellen aktiv waren). Und wir erreichen noch etwas: Durch die sehr langsame Führung des Prozesses bleibt das System immer im energetisch günstigsten Zustand. Das ist die Aussage des sogenannten adiabatischen Theorems – das beweise ich jetzt aber nicht. Anschaulich ist es eigentlich aber ganz leicht zu verstehen: Stellt euch als Beispiel für ein System im energetisch günstigsten Zustand mal wieder einen Ball vor, der in einer Mulde liegt. Wenn ihr die Form der Mulde sehr langsam ändert, dann bleibt der Ball die ganze Zeit am tiefsten Punkt – ändert ihr die Form der Mulde dagegen schnell, dann könnt ihr den Ball damit wegschießen. (“Adiabatisches Theorem” ist übrigens ein blöder Name – es ist ja nicht das Theorem, das adiabatisch ist…)
Alles in allem haben wir jetzt also zwei Quellen, die wir irgendwann aufdrehen und dann in ferner Zukunft wieder zu Null zurückstellen. Dieses Bild hier soll das veranschaulichen:
Unsere Extradrehung wird jetzt etwas komplizierter. Im Bild oben war ja schon zu sehen, dass es einen nennenswerten Einfluss der beiden Quellen aufeinander nur dann gibt, wenn sie im passenden Raumzeitabstand zueinander liegen. Wenn jetzt unsere Quellen über einen längeren Zeitraum aktiv sind, dann gibt es natürlich sehr viele Möglichkeiten, mit Hilfe des Propagators Einfluss aufeinander zu nehmen, etwa so:
Und das sind natürlich nicht alle – wir müssen jede Kombination von Start- und Zielpunkten des Propagators berücksichtigen, die im erlaubten Zeitintervall liegen und bei x anfangen und bei y aufhören.
Streng genommen müssten wir sogar auch diejenigen Kombinationen berücksichtigen, die bei x anfangen und aufhören und ebenso für y. Das wären aber sogenannte Selbstenergieterme, die nichts mit der Wechselwirkung zwischen x und y zu tun haben, die lasse ich deshalb in der Rechnung unter den Tisch fallen.
Mathematisch wird das – wie immer, wenn man über alles Mögliche summiert – wieder ein Integral, genauer gesagt sogar zwei Integrale, eins für die eine und eins für die andere Quelle. Dieses Integral kann man lösen, wobei man sich für den Propagator wieder der Fourier-Transformation bedient. Die Details verbanne ich in einen Abschnitt für Fortgeschrittene, weil im Moment nur das Ergebnis wichtig ist.
Die Rechnung klaue ich in zwei Büchern, dem viel-zitierten von Zee (“Quantum Field Theory in a Nutshell”) und M. Stone “The physics of Quantum Fields”, das auch ziemlich gut ist (wenn auch nicht ganz so gut wie das von Zee – es rechnet alles im kanonischen Formalismus mit Auf- und Absteigeoperatoren (vielleicht erkläre ich die auch noch irgendwann) statt mit Pfadintegralen).
Also los. Wir fangen an mit der Formel für W(J), den Extra-Phasenfaktor durch die Quellen:
Die Quellen sitzen bei x und y, wir können sie also als Jδ(x) und Jδ(y) umschreiben (δ ist die Dirac-Delta-Funktion (oder Distribution)), dann fallen die räumlichen Integrale weg, das J gibt dann die Stärke der Quellen an, die ich der Einfachheit halber als gleich annehme.
Wenn ich das einsetze, sieht das Ergebnis so aus:
Der Faktor 1/2 fällt weg, weil wir beide x-y-Kombinationen berücksichtigen müssen.
Für den Propagator setzen wir seine Fourier-Transformierte ein:
Sieht gruselig aus, ist es aber nicht, jedenfalls nicht zu sehr. Wir können das Integral über y0 benutzen, um den ersten Exponentialterm loszuwerden (das gibt eine Delta-Funktion, die k0 zu Null setzt.). Dann bleibt
Dabei habe ich das iε weggelassen, weil der Nenner jetzt eh nie Null werden kann. Außerdem habe ich (weil k2 ja ein Vierervektor-Produkt war) im Nenner das Vorzeichen gedreht und dafür das Vorzeichen Vorn weggelassen.
Das zweite Integral (über k) lässt sich lösen (das verbannt selbst Zee in einen Anhang – im wesentlichen ist der Trick, dass man in Kugelkoordinaten transformiert)
Dabei ist r der (skalare) räumliche Abstand zwischen x und y.
Und was ist mit dem Integral über x0? Ist das nicht unendlich? Nein, ist es nicht – es kommt ja vom Integral über die Quellen. Wenn die Quellen ausgeschaltet sind, sind alle Quellterme Null. Also laufen die Integralgrenzen nicht von minus unendlich bis unendlich, wie man bei meiner schlampigen Schreibweise denken könnte, sondern sie laufen von “vor langer Zeit” bis “in ferner Zukunft”. Nennen wir dieses Zeitintervall T, dann ist das Integral also einfach gleich T.
Das Ergebnis dieser langen Rechnung gehört aber definitiv in den allgemeinen Teil.
Auch wenn die Rechnung nicht hier in den harmlosen Teil gehört, das Ergebnis sollten wir uns anschauen:
In dieser Formel stecken ein paar Zeichen drin, die ich während der fiesen Rechnung eingeführt habe, die muss ich natürlich erklären. T ist die Zeitdauer, die die Quellen angeschaltet waren (also in den Diagrammen oben die Länge der vertikalen Linie, das sind ja Raumzeitdiagramme, wo die senkrechte Richtung die Zeit darstellt). J gibt die Stärke der Quellen an (denkt im Zweifel an so etwas wie Massen oder elektrische Ladungen, die sind ja auch nicht alle gleich groß), wobei ich angenommen habe, dass unsere beiden Quellen hier gleich stark sind (sonst stünde hier J1J2).
Der Buchstabe r bezeichnet den räumlichen Abstand zwischen den beiden Quellen.
Was sagt uns die Formel für W(J)? W(J) war ja der zusätzliche Drehwinkel der Amplitude. Wir sehen, dass dieser Drehwinkel von der Stärke der beiden Quellen abhängt – das erscheint ja ganz logisch, je stärker die sind, desto stärker der Einfluss. Außerdem hängt er von der Zeit ab, die die Quellen eingeschaltet waren – ist auch ganz plausibel, wenn ich etwas doppelt so lange tue, bekomme ich doppelt so viel Ergebnis. (Im Pfadintegral rotiert der Phasenfaktor mit einer bestimmten Geschwindigkeit, doppelt so lange rotieren ergibt doppelt so viel Drehung.)
Dann kommt der Bruch. Da steht unten im Nenner ein Faktor r – W(J) wird also immer kleiner, je größer der Abstand der Quellen wird. Oben im Zähler steht auch noch ein Faktor mit einer Exponentialfunktion. Die hat ein negatives Argument, nämlich -mr. Das m ist die Masse unseres Quantenfeldes (der “Extra-Term”), r wieder der Abstand. W(J) nimmt also exponentiell mit dem Abstand ab – wie stark, hängt von der Masse ab. Dieses Bild zeigt die Funktion (in absolut willkürlichen Einheiten) für unterschiedliche Werte der Masse m:
Ist die Masse groß, ist die Abnahme rapide, ist sie klein, ist die Abnahme schwächer. Bei Masse gleich Null fällt die Funktion ab wie 1/r (der Exponent ist immer gleich 1). Für sehr kleine Abstände dagegen wird der Wert der Funktion sehr groß.
Wenn wir annehmen, dass wir den (von mir immer noch nicht spezifizierten) Effekt, den die Quellen aufeinander ausüben, nicht mehr messen können, wenn W(J) sehr klein wird, dann haben wir also einen Effekt, dessen Reichweite mit der Entfernung und mit der Masse abnimmt. Ist die Masse groß, ist die Reichweite klein, bei Masse Null ist die Reichweite anscheinend sehr groß.
Vorher aber sollte ich endlich mal konkret werden. Was ist denn nun die physikalische Bedeutung von W(J)? Ein globaler Phasenfaktor an einer Wahrscheinlichkeitsamplitude klingt jetzt erst einmal wenig spektakulär und ziemlich abgehoben. Tatsächlich hat dieser Phasenfaktor aber eine ganz einfache und anschauliche Bedeutung.
Wer die Serie aufmerksam verfolgt hat, der wird jetzt vermutlich sagen: Die Bedeutung ist doch eigentlich klar – war nicht der Phasenfaktor immer gerade die Wirkung? Gut aufgepasst, aber leider trotzdem nicht ganz richtig. Wenn wir im Pfadintegral einen einzelnen Pfad betrachten, dann ist der Phasenfaktor die Wirkung. Hier aber betrachten wir jetzt die Summe über alle Pfade, um die Gesamtamplitude für den Prozess zu berechnen. Deshalb ist der Phasenfaktor nicht direkt die Wirkung, sondern etwas, das eng mit der Wirkung zusammenhängt: Die Energie.
Genauer gesagt ist W(J)=-ET. (Im Buch von Zee ist hier ein Vorzeichenfehler, ich hoffe, ich habe alle Vorzeichen hier richtig zusammengebastelt) Dabei ist T wieder das Zeitintervall und E ist die Energie. (Warum das so ist, und welche Energie hier eigentlich gemeint ist, dazu gleich mehr.) Wir haben also
Immerhin – die Energie ist eine “echte” physikalische Größe, unter der wir uns etwas vorstellen können. Bevor wir uns das genauer ansehen, will ich versuchen, euch zumindest plausibel zu machen, warum der Phasenfaktor etwas mit der Energie zu tun hat. Wer’s einfach glauben mag, der kann den nächsten Abschnitt schadlos überspringen.
Die Energie als Phasenfaktor
Tja, hier habe ich nun ein kleines Problem: Dass die Energie in einem Problem als Phasenfaktor auftauchen muss, ist so tief in den Wurzeln der Physik verankert, dass es gar nicht so leicht ist, eine Begründung dafür zu finden.
Der Phasenfaktor, den wir hier haben, ist ja ET, Energie mal Zeit. (Da fehlt natürlich wieder ein ℏ.) Ich verwende jetzt mal eine Schreibweise aus der Quantenmechanik, um die Argumentation übersichtlich zu halten. Ich bezeichne einen Zustand unseres Quantenfelds dadurch, dass ich ihn in eine halbe spitze Klammer einschließe (ein “ket”). Den Vakuum-Zustand, um den es hier geht, bezeichne ich mit |0>.
Wenn wir keine Quellen einschalten, dann bleibt das Vakuum einfach Vakuum, wenn wir das Zeitintervall T abwarten:
Wenn wir dagegen unsere Quellen an- und wieder abschalten, dann bekommen wir ja den zusätzlichen Phasenfaktor W(J):
Sieht mal wieder schlimmer aus, als es ist – der Pfeil sagt einfach, dass wir das Zeitintervall T mit angeschalteten Quellen J abwarten; und das e-hoch-i W(J) ist nichts als unsere Schreibweise für einen Phasenfaktor, die wir in einem der ersten Teile eingeführt haben, also die Extra-Drehung der Amplitude.
Wir haben hier also einen Zustand – das Vakuum – der nach einer Zeit T in einen anderen Zustand – das Vakuum mit Extra-Phasenfaktor – übergeht. Hier steht also nichts, was wir nicht schon wissen.
Eine Möglichkeit, einzusehen, dass es sich bei diesem Phasenfaktor um die Energie handelt, besteht darin, eine Anleihe in der guten alten Quantenmechanik zu machen – letztlich ist unsere Quantenfeldtheorie ja nichts anderes als Quantenmechanik mit zwei Extras: Relativitätstheorie und Feldern statt Punktteilchen.
Unser Vakuum ist ein Zustand mit einer Energie – nämlich der niedrigst-möglichen Energie. Diese Energie steckt auch in der Quantenmechanik in einem Phasenfaktor drin: Dort haben die Wellenfunktionen (die ja die Zustände beschreiben) zu einem Zustand mit einer bestimmten Energie auch immer einen Phasenfaktor, nämlich
Das kann man direkt aus der Schrödingergleichung ableiten. In der Quantenmechanik ist ein Phasenfaktor also eine Energie (das sieht man auch an der berühmten Beziehung E=ℏω).
Man mag jetzt einwenden, dass die Schrödinger-Gleichung in der Quantenfeldtheorie ja gerade nicht gilt – man kann dasselbe aber auch für die Klein-Gordon-Gleichung zeigen.
Man kann das Argument auch umdrehen: Die Schreibweise mit dem Pfeil oben zeigt ja, dass der Phasenfaktor das ist, was man bekommt, wenn man die Zeit fortschreiten lässt. Manche Bücher der Quantenmechanik gehen deshalb andersherum vor: Sie definieren eine Zeitentwicklung, die einen Zustand |ψ(t=0)> in einen späteren Zustand |ψ(t=T)> überführt, und leiten dann ab, dass das mathematische Objekt, das die Zeitentwicklung regelt, gerade die Energie (genauer gesagt, der Energieoperator) ist:
Das E mit dem Dach drauf ist der Energie-Operator. Wenn der Zustand ψ eine definierte Energie hat, dann kann man das Dach am Energieoperator auch weglassen und den direkt durch die Energie ersetzen. Auf diesen Zugang hat mich Leser Christian hier aufmerksam gemacht. (Nochmal danke an alle, die sich an der Diskussion dort beteiligt haben.)
Diese Denkweise führt dann, wenn ich es richtig sehe, direkt zur Aussage von Wigner, dass Elementarteilchen irreduzible Darstellungen der Poincare-Gruppe sind. Obwohl das richtig ist, konnte ich mich mit dieser Aussage noch nie anfreunden – vielleicht ist das auch der Kern meines Problems hier.
Mit diesem Argument hängt auch ein anderer Aspekt zusammen: Für Energie und Zeit gilt (ebenso wie für Ort und Impuls) eine Unschärferelation: Man kann die Energie eines Zustands nur dann exakt bestimmen, wenn man dafür unendlich lange Zeit hat, und es gilt ΔEΔt≥ℏ/2.
Es gibt hier auch eine enge Verbindung zum berühmten Noether-Theorem, nach dem die Energie eines Systems genau dann erhalten ist, wenn es bei einer zeitlichen Verschiebung unverändert bleibt.
Vielleicht macht euch das zumindest plausibel, warum Energie und Zeitentwicklung hier so eng zusammenhängen. Aber ich geb’s zu: So ganz zufrieden bin ich mit all diesen Halb-Erklärungen nicht. Es gibt zwei Möglichkeiten, warum das so ist: Entweder ich verstehe es noch nicht wirklich gut genug oder diese Ideen sind mir so selbstverständlich, dass es mir schwer fällt, mich in jemanden hineinzuversetzen, der diese Konzepte nicht kennt (das alte Problem, dass wohl jeder Lehrende kennt). Vielleicht fällt mir irgendwann noch etwas besseres ein, dann schreibe ich einen Text dazu, warum Energie und Zeit so merkwürdig eng verbandelt sind.
Energie und Kraft – wir verdienen uns – fast – einen Nobelpreis
Wir haben also mit angeschalteten Quellen eine Energie, die durch diese Formel gegeben ist (ausnahmsweise bastele ich die Konstanten zumindest im Exponenten mal wieder rein, ich hoffe, ich habe mich nicht vertan):
Das Vorzeichen hier ist negativ, die Energie des Systems ist mit eingeschalteten Quellen also kleiner als ohne diese Quellen. Wenn wir versuchen würden, die Quellen voneinander zu entfernen (sehr langsam, sonst kann alles mögliche passieren, das ist wieder das “adiabatische Theorem”), dann müssen wir dafür Energie aufwenden, das heißt, wir müssen Arbeit leisten, denn die Energie wäre ja hinterher größer als vorher.
Nach der guten alten klassischen Physik hängt die Arbeit, die man an einem System leisten muss, mit der Kraft zusammen: Arbeit ist Kraft mal Weg. Wenn wir die Quellen ein Stück voneinander entfernen wollen, brauchen wir also eine Kraft. Mit anderen Worten: Die beiden Quellen ziehen sich an.
Aus unserer Quantenfeldtheorie haben wir also ein echtes physikalisches Resultat abgeleitet: Zwei Quellen, die mit unserem Quantenfeld wechselwirken, ziehen sich an. Die Anziehungskraft nimmt dabei mit dem Abstand ab.
Der japanische Physiker Hideki Yukawa, der von Studenten angeblich wegen seiner komplizierten Mathematik “headache-Yukawa” genannt wurde – eine Geschichte, die ich in irgendeinem Buch gelesen habe, die aber durch eine Recherche bei der google University auf die Schnelle nicht bestätigt wurde – also, dieser Hideki Yukawa hat in den dreißiger Jahren eine Rechnung ähnlich wie diese hier angestellt und sich dann Folgendes überlegt: Eine anziehende Kraft, die mit der Entfernung sehr schnell abnimmt – so etwas beobachtet man doch auch in der Natur. Kernbausteine (Protonen und Neutronen) halten in Atomkernen fest zusammen, aber die Reichweite der Kernkraft ist sehr gering, Atomkerne sind immer klein und wenn sie zu groß werden, werden sie instabil und zerfallen radioaktiv.
Ausgehend von dem, was Yukawa über die Kernkraft wusste, konnte er ableiten, dass das zu dieser Rechnung hier passte. Dann würde die Kernkraft durch ein Quantenfeld vermittelt werden, und zu diesem Feld gehört dann ein Teilchen der Masse m. Yukawa schätzte die Masse dieses neuen Teilchens ab und sagte damit das Pion vorher, das dann 1947 auch gefunden wurde, und zwar ziemlich gut passend zur vorhergesagten Masse. Für diese Vorhersage hat Yukawa auch postwendend den Nobelpreis bekommen.
Zumindest ganz grob können wir seine Rechnung mit einer Abschätzung nachvollziehen – dazu ignorieren wir spaßeshalber den Nenner und schauen uns nur den exponentiellen Abfall im Zähler an. Dort steht ja als Argument -mcr/ℏ. Bei Abstand Null ist dieser Term gleich 1 (der Nenner unseres Bruchs divergiert, aber das ignoriere ich mal kurzerhand.) Wenn wir annehmen, dass die Reichweite dieser Kraft der Größe eines Uranatomkerns (mit einem Durchmesser von 10 Femtometern (10-14 Metern)) entspricht, dann sollte 1/(mc/ℏ) also in dieser Größenordnung liegen, dann ist der Exponent gerade -1. Setzt man Zahlenwerte ein, dann bekommt man für m eine Masse von etwa 50 Elektronenmassen. Das ist natürlich eine sehr grobe Abschätzung (wir haben ja auch den Nenner ignoriert, und ein Abfall um 1/e=0.37 ist ja auch nicht viel) – der tatsächliche Wert liegt bei etwa 240 Elektronenmassen, aber immerhin haben wir die Größenordnung richtig hinbekommen.
Ich gebe zu, es hat lange gedauert (ursprünglich dachte ich, dass ich in dieser Serie etwa 7 Teile brauche, bis wir hier ankommen), aber nun haben wir aus unserer Quantenfeldtheorie etwas Faszinierendes abgeleitet: Anziehungskräfte zwischen Objekten können dadurch entstehen, dass sie mit einem Quantenfeld wechselwirken. Unser φ-Feld sorgt für eine anziehende Wechselwirkung, die Energie ist negativ. Und nimmt man an, dass so ein Feld für die Kernkraft verantwortlich ist, bekommt man einigermaßen plausible Resultate heraus und kann sogar ein neues Elementarteilchen vorhersagen.
Aus dem Alltag kennen wir eine andere anziehende Wechselwirkung: Die Schwerkraft. Hier ist die Reichweite allerdings unendlich – die Energie fällt wie 1/r ab, so dass wir annehmen müssen, dass das zugehörige Quantenfeld (die Gravitonen) keine Masse hat.
Wir kennen aber auch eine Wechselwirkung, die anders funktioniert, bei der sich nämlich gleichartige Quellen (Ladungen) abstoßen: Die elektrische Kraft. Auch sie hat unendliche Reichweite, denn die vermittelnden Teilchen sind die masselosen Photonen – und anders als bei der Schwerkraft kennen wir hier die zugehörige Quantenfeldtheorie auch sehr genau.
Woran liegt es, dass Kernteilchen sich anziehen, gleiche elektrische Ladungen sich abstoßen, aber Massen wiederum immer anziehend wirken? Lässt sich das auch mit der Quantenfeldtheorie wiedergeben?
Die gute Nachricht lautet: Ja, das geht. Ein subtiles Wechselspiel zwischen Relativitätstheorie und dem berühmten “Spin” von Teilchen (und Quantenfeldern) sorgt genau für das richtige Vorzeichen der Kraft. Ob es mir gelingt, das zu erklären? Warten wir’s ab…






Kommentare (56)