Die (vermutliche) Entdeckung des Higgsteilchens hat ja zu einigen Diskussionen geführt – kann man das Higgsteilchen verstehen? Harald Lesch ist der Ansicht, 99,9% der Menschen könnten das nicht, ich habe mich ganz anders geäußert und behauptet, dass jeder es zumindest “ein bisschen” verstehen kann. Die große Diskrepanz zwischen diesen unterschiedlichen Lagern hat vermutlich weniger etwas mit dem Higgsteilchen zu tun und mehr mit der Frage, was man eigentlich meint, wenn man etwas “versteht”. Anhand des Higgsteilchens möchte ich hier unterschiedliche Aspekte oder Stufen des Verstehens auseinanderdröseln.
(Einige Aspekte habe ich vor langer Zeit schon angesprochen, als ich mir Gedanken gemacht habe, was eigentlich Anschaulichkeit ist.)
Vermutlich hat jeder, der nicht gerade in einer Höhle ohne Stromanschluss wohnt, mitbekommen, dass da etwas entdeckt wurde und dass dieses Etwas zumindest für die PhysikerInnen wichtig ist und ihre Theorien bestätigt. In gewisser Weise ist das wohl schon die erste Stufe des Verstehens:
Erkennen, dass da überhaupt etwas zu verstehen ist.
Auch das ist ja schon nicht ganz selbstverständlich – viele Erkenntnisse der Wissenschaft beruhen ja auch darauf, dass überhaupt erst einmal erkannt wurde, dass es da ein Phänomen gibt, das verstanden werden will.
Gut, es gilt also, das Higgsteilchen zu verstehen. Die nächste Stufe besteht jetzt wohl darin zu
Verstehen, welche Rolle es in der Natur (und der physikalischen Theorie) spielt.
In diese Kategorie gehört meine Kurz-Kurz-Erklärung, aber auch die ganzen Analogien mit Prominenten auf Parties oder mit Kugeln, die durch Honig fliegen. Diese Erklärungen sollen die wichtigste Eigenschaft des Higgsfeldes deutlich machen: Das Higgsfeld verleiht Elementarteilchen ihre Masse.1
Das Higgsteilchen ist eine messbare Anregung des Higgsfeldes, es ist sozusagen eine Störung in dem vollkommen gleichartigen Higgsfeld, die man deswegen sehen kann.
1Dabei wird übrigens meist unterschlagen, dass der größte Teil der Masse, die wir beobachten, nicht vom Higgsfeld erzeugt wird (rühmliche Ausnahme ist der ZEIT-Artikel von dieser Woche). Der Großteil der Masse von Atomen steckt im Atomkern und beruht auf der Energie der Bindung der Quarks innerhalb der Protonen und Neutronen; nur ein relativ kleiner Teil der Masse ist “echte” Masse. Das sollte ich vielleicht bei Gelegenheit auch noch mal ausführlich erklären. Die Aussage, dass unsere Welt ohne Higgsfeld vollkommen anders aussähe, bleibt aber richtig – Atomkerne hätten immer noch eine Masse, Elektronen aber nicht. Chemie wie wir sie kennen wäre dann nicht möglich.
Auch wenn diese Erklärung (ohne die Fußnote) schon ein bisschen Nachdenken erfordert, denke ich, dass sie prinzipiell auch für jemanden nachvollziehbar ist, der nicht Physik studiert hat. In diesem Sinne kann dann eben jeder das Higgsteilchen verstehen.
Dass Menschen wie der Interviewpartner von Lesch sagen, sie würden diese Erklärung selbst nicht verstehen, liegt vermutlich an zwei Dingen: Zum einen ist sie (gerade wenn man Anlogien wie Honig oder Parties verwendet) ganz offensichtlich eher metaphorisch, denn das Universum ist ja nicht wirklich von Honig durchzogen (und Party ist auch nicht überall). Zum anderen – und das ist vermutlich noch wichtiger – ist es eine Erklärung, mit der man wenig anfangen kann.
“Anfangen” ist hier in dem Sinne gemeint, dass man diese Erklärung zwar so schlucken kann, wie sie ist, aber man hat nicht genügend Informationen, um weiterdenken zu können. Wenn ich jemanden, der diese Erklärung bekommen hat, bitte, sich eine Eigenschaft der Higgsfeldes zu überlegen (z.B. bei der Honig-Analogie die Frage: Warum werden dann nicht alle Teilchen so abgebremst, dass sie zur Ruhe kommen?), dann merkt derjenige schnell, dass er darauf keine (oder eine offensichtlich falsche) Antwort hat.
Und hinzu kommt, dass auch immer noch nicht klar ist, warum das so sein soll. Warum können die Teilchen nicht einfach selbst eine Masse haben und brauchen dafür erst ein Higgsfeld? Das bringt uns zur nächsten Stufe des Verstehens:
Verstehen, wozu das Higgsteilchen “erfunden” wurde
Bis in die sechziger Jahre hinein hat niemand ein Higgsfeld gebraucht. Teilchen hatten einfach eine Masse, die als Faktor in der entscheidenden Gleichung der Quantentheorie (der Formel für die Lagrangedichte, falls jemand gern coole Fachausdrücke hört) auftauchte und damit konnte man das Verhalten von Elektronen und anderen Teilchen prima beschreiben.
Dann aber merkte man, dass die Radioaktivität die merkwürdige Eigenschaft hat, dass es Prozesse gibt, die nicht mehr ablaufen können, wenn man das beobachtete System einfach spiegelt. Das ist ungefähr so (Vorsicht, hier kommt wieder eine Analogie) als würden es die Gesetze der Mechanik zwar erlauben, normale Uhren zu bauen, aber solche, die gegen den Uhrzeigensinn drehen, wären einfach unmöglich.
Als man nun versuchte, eine Theorie zu formulieren, die diese Eigenschaft hat und auch ansonsten zu den Beobachtungen passte, merkte man schnell, dass das nur dann funktioniert, wenn alle Teilchen masselos sind. Deswegen erfand man den Higgsmechanismus. (Dieses Erklärungsniveau entspricht ungefähr dem meiner Kurzerklärung. In der Langfassung habe ich auch noch ein bisschen erklärt, warum das so ist, warum also Teilchen in einer solchen Theorie masselos sein müssen.)
Verstehen, wie das Higgsteilchen prinzipiell wirkt
O.k., das Higgsfeld verleiht allen Elementarteilchen Masse. Aber wie funktioniert das? Wie kann die Wechselwirkung mit einem Feld so aussehen wie eine Masse, also für Phänomene wie die Trägheit sorgen?
Das zu verstehen beinhaltet zwei Bestandteile. Zum einen muss man verstehen, wie “Masse” sich überhaupt auf der Ebene der Elementarteilchen äußert.1 Dazu muss man ein bisschen tiefer in die Quantentheorie einsteigen. Dann sieht man, dass “Masse” sich in diesen Theorien in einer Weise äußert, die man grafisch so darstellen kann:
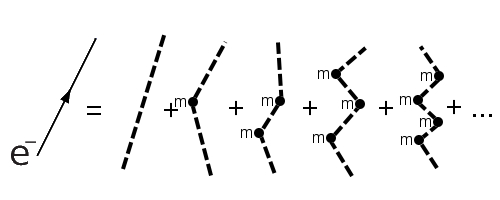
Hier fliegt links vom Gleichheitszeichen ein Elektron von A nach B. Man kann diesen Prozess auch darstellen wie auf der rechten Seite – dabei ist die gestrichelte Linie ein Elektron ohne Masse, und die kleinen Knubbel mit dem “m” dran sind eine grafische Darstellung dafür, wie die Masse hier eingeht. Eine weniger schwammige Erklärung des Bildchens findet ihr hier
1Dabei ist hier immer nur der Aspekt der Trägheit gemeint – wie Elementarteilchen mit Gravitationsfeldern wechselwirken, steht auf einem anderen Blatt, das wir leider noch nicht zu lesen bekommen haben, das ist die noch nicht gefundene Theorie der Quantengravitation.
Die Wechselwirkung mit dem Higgsfeld sieht jetzt ganz ähnlich aus (auch das erkläre ich etwas ausführlicher in der Langfassung des Higgs-Textes):
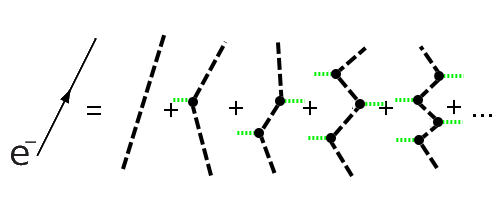
Statt der Knubbel mit dem Massenwert “m” dran haben wir jetzt eine Wechselwirkung mit dem (grün gestrichelten) Higgsfeld. Auf diesem Niveau hat man schon eine ganze Menge verstanden: Man sieht, dass die Wechselwirkung mit dem Higgsfeld wie eine Masse wirken kann und kann daraus folgern, dass die Stärke der Wechselwirkung mit dem Higgsfeld sagt, wie groß die Masse eines Teilchens ist.
Die Erklärung hier ist schon ziemlich involviert, kommt aber immer noch ohne viel Mathematik aus (und wer meine Quantenfeldtheorie-Serie gelesen hat, der sollte sie hoffentlich halbwegs nachvollziehen können). Die meisten PhysikerInnen würden aber sicher sagen, dass ein echtes Verständnis des Higgsfeldes nur auf mathematischer Ebene funktionieren kann.
Der nächste Schritt ist deshalb:
Verstehen, wie genau das Higgsfeld in dieser Weise wirken kann
Warum gerade ein Higgsfeld? Warum gibt es genau eine Anregung des Higgsfeldes, die man als Teilchen sehen kann, also nur eine Sorte Higgsteilchen? Wie passt das Higgsfeld genau in die Theorie und wie genau kann man mit dem Higgsfeld zum Beispiel die Masse von Teilchen berechnen? Wie stark ist das Higgsfeld?
Das sind alles Fragen, die man nur mit Hilfe der mathematischen Formulierung der Theorie beantworten kann. Wer dieses Niveau des Verstehens erreichen will, der muss deshalb mathematisch fit genug sein, um Gleichungen wie diese verstehen zu können:
Lagrangedichte des Standardmodells, von hier geklaut (ich übernehme keine Garantie, dass die Gleichung nicht etwas vereinfacht ist, ich habe nicht alle Terme geprüft).
Diese Stufe des Verständnisses ist sicherlich viel tiefer als die vorhergehenden, oder?
Das sollte zumindest so sein – die Erfahrung (auch meine eigene) zeigt aber, dass das nicht unbedingt so ist. Viele Lehrbücher und viele Profs in ihren Vorlesungen erklären nämlich überhaupt nur die Mathematik hinter solchen Theorien, ohne die Zusammenhänge auch anschaulich zu erklären. Das führt dazu, dass Physikstudis dann zwar die Gleichungen nachrechnen können, aber trotzdem nicht einfach oder anschaulich erklären können, was die Gleichungen aussagen. Das ging mir selbst während des Studiums manchmal auch so – ich konnte komplizierte Gleichungen nachrechnen, hatte aber kein wirkliches Verständnis für das, was die Gleichungen bedeuten, und hätte aus den Gleichungen deswegen Erklärungen wie die oben gegebenen nicht ableiten können. Das ist eins von vielen Beispielen für die oft furchtbar schlechte Didaktik der Physik.
Nehmen wir aber an, jemand hätte all diese Verständnisebenen einigermaßen verinnerlicht – er oder sie kann die Gleichungen nachvollziehen und daraus auch anschauliche Erklärungen ableiten. Nach viel Mühe ist das etwa das Niveau auf dem ich mich befinde (auch wenn ich die Gleichung oben auch nicht ohne nachzuschlagen interpretieren oder damit gut herumrechnen könnte) – das sage ich aber nicht, um anzugeben, denn wie ihr gleich sehen werdet, ist das noch nicht das Ende der Verstehens-Fahnenstange. Nimmt mir nämlich jemand meine Bücher weg, dann bin ich aufgeschmissen. Die Rechnungen sind zu lang, als dass ich sie auswendig könnte (wäre auch wenig hilfreich), und mein Verständnis hat nicht die nächste Stufe erreicht.
Verstehen, wie man das Higgsfeld herleitet
Diese Stufe ist nämlich erst dann erreicht, wenn ihr selbst die Gleichungen nicht bloß nachvollziehen könnt, wenn sie vor euch stehen, sondern wenn ihr sie selbst herleiten könnt, nur an Hand der prinzipiellen Idee, wie das Higgsfeld funktioniert.
Der Physiker Richard Feynman war bekannt dafür, dass er diese Art des Verstehens bevorzugte: Wenn er von einer neuen Theorie hörte, dann versuchte er, nur die Idee aufzuschnappen und sich dann die Theorie selbst noch einmal herzuleiten. (Wenn ihr allerdings kein Genie seid, dann dürfte euch das seeehr viel Zeit kosten oder auch gar nicht klappen.) Auf diese Weise hat er die Theorie natürlich in noch viel fundamentalerer Weise verstanden (ob Feynman das beim Higgsteilchen so gemacht hat, weiß ich nicht, in vielen anderen Fällen aber schon).
Auf der Tafel in Feynmans Büro fand man bei seinem Tod die Sätze (ein Bild und einen Artikel dazu findet ihr hier)
“What I cannot create, I do not understand.”
[Was ich nicht erschaffen kann, verstehe ich nicht.]und
“Know how to solve every problem that has been solved.”
[Wissen, wie man jedes jemals gelöste Problem löst.]
Über die Bedeutung dieser Sätze ist oft spekuliert worden, aber ich gehe davon aus, dass sie in genau dieser Weise gemeint sind: Man versteht eine Theorie nur dann, wenn man sie selbst an Hand der Idee auf einem Blatt Papier wieder aufstellen und nachrechnen kann. Das ist sicherlich eine sehr tiefe Art des Verstehens und es gibt vermutlich nicht allzu viele Menschen, die das Higgsteilchen in dieser Weise in allen Einzelheiten verstehen.
Es ist aber immer noch nicht das Höchste der Gefühle.
Das Higgsfeld intuitiv verstehen
Der höchste Grad des Verstehens ist vermutlich erst dann erreicht, wenn man ein intuitives Gefühl dafür hat, wie die Theorie (in diesem Fall das Higgsteilchen) funktioniert. Der Physiker Paul A. M. Dirac hat einmal gesagt
I consider that I understand an equation when I can predict the properties of its solutions, without actually solving it.
[Ich gehe davon aus, dass ich eine Gleichung verstehe, wenn ich die Eigenschaften ihrer Lösungen vorhersagen kann, ohne sie tatsächlich zu lösen.]
Um die Theorie wirklich zu verstehen, muss man sie soweit verinnerlicht haben, dass man die Lösung eines Problems “sieht”, dass man schon weiß, was herauskommen wird, bevor man anfängt zu rechnen.
Von Feynman gibt es eine ähnliche Aussage. Als er nach einem wichtigen Satz der der Quantentheorie (dem Spin-Statistik-Theorem) gefragt wurde, versprach er, darüber eine Vorlesung für Studienanfänger zu halten. Einige Tage später sagte er
I couldn’t reduce it to the freshman level. That means we really don’t understand it.
[Ich konnte es nicht auf Anfängerniveau herunterbrechen. Das bedeutet, dass wir es nicht wirklich verstehen.]
Das kennt vermutlich jeder, der selbst Vorlesungen hält oder Blogeinträge schreibt: Man denkt, man hat etwas verstanden, aber wenn man versucht, es anderen möglichst einfach zu erklären, dann merkt man plötzlich, dass da doch noch Lücken sind. (Ein probates Mittel, wenn ich mit einem Problem gar nicht weiterkomme, ist deswegen immer, es jemand anderem zu erklären zu versuchen. Oft merke ich dann beim Erklären selbst, wo die Schwierigkeit steckt.)
Verstehen und Vorhersagen
Die unterschiedlichen Stufen des Verstehens machen eins in meinen Augen ganz deutlich: Je tiefer das Verständnis ist, um so mehr kann man damit anfangen. Die ganz simple Honig-Analogie ist nahezu nutzlos, weil sie sofort zu Widersprüchen führt, wenn man sie weiterdenkt (Warum stoppen nicht alle Teilchen im Honig?), aber immerhin ermöglicht es einem, eine Idee zu haben, was die PhysikerInnen mit dem Higgs überhaupt bezwecken.
Diesen Aspekt versteht man auf der nächsten Ebene besser, und kann dann zumindest folgern, dass tatsächlich alle Teilchen masselos sein müssen. Auf den weiteren Ebenen versteht man dann auch, dass die Masse direkt mit der Stärke der Wechselwirkung mit dem Higgsfeld zusammenhängt, man versteht dann (mathematisch), wie einzelne Teile des Higgsfeldes von anderen Teilchen “gefressen” werden und so weiter. Auf der letzten Ebene angekommen kann man dann vielleicht sogar neue Theorien ableiten für den Fall, dass das gefundene Teilchen doch nicht die erwarteten Eigenschaften hat.
Was wir im Kopf haben, ist immer ein Modell der Wirklichkeit, ein Abbild dessen, was in der realen Welt passiert. (Ich stelle mich hier der Einfachheit halber auf den Standpunkt, dass es eine solche “reale Welt” wirklich gibt.) Je besser wir etwas verstehen, desto genauer ist dieses Abbild der realen Welt, und desto besser können wir vorhersagen, was in der realen Welt passieren wird, indem wir die Objekte in unserer Vorstellung manipulieren.
“Verstehen” hat deswegen immer etwas mit “vorhersagen” zu tun – je tiefer das Verständnis, desto besser kann ich bestimmte Aspekte der Theorie (und damit der Wirklichkeit) vorhersagen. Das gilt nicht nur in der Physik, sondern auch in anderen Wissenschaften, selbst in solchen, in denen man zunächst erwarten könnte, dass man dort nichts vorhersagen kann, weil sie sich mit der Vergangenheit beschäftigen, beispielsweise der Geschichtswissenschaft oder der Paläontologie. Obwohl die Dinosaurier (bis auf die Vögel natürlich) ausgestorben sind, können wir die Evolution der Dinos verstehen, und das erlaubt uns, gewisse Vorhersagen zu machen. Als die ersten Dinosaurier mit Federn entdeckt wurden, war das zwar eine Sensation, aber für viele auch eine Bestätigung dessen, was sie lange erwartet hatten. Und wir verstehen die Evolution der Dinos gut genug, dass die meisten neuen Fossilienfunde zwar spannend, aber nicht vollkommen überraschend sind, sondern sich gut in unser Wissen einfügen.
Verstehen ist also immer etwas Operatives – ich verstehe etwas, wenn ich mir vorstellen kann, wie dieses etwas sich in gewissen Situationen verhalten wird. Ein oberflächliches Verständnis beschränkt sich auf ein bloßes Nachvollziehen von Gedanken, aber je tiefer das Verständnis wird, desto mehr kann ich damit anfangen und desto besser kann ich vorhersagen, was unter bestimmten Bedingungen passieren wird.
Kann man also das Higgsteilchen verstehen?
Das kommt anscheinend ganz darauf an, auf welchem Niveau sich dieses “Verstehen” abspielen soll – ein gewisses Grundverständnis kann vermutlich fast jeder gewinnen, auf mathematisch tiefer Ebene dürften es tatsächlich nur sehr wenige Menschen sein, die das Higgsteilchen wirklich verstehen. Und angesichts der Komplexität der Theorie ist es nicht ausgeschlossen, das morgen irgend eine schlaue Physikerin eine Konsequenz der Theorie berechnet, an die bisher noch niemand gedacht hat – dann müsste man sagen, dass niemand das Higgsteilchen vollkommen versteht.

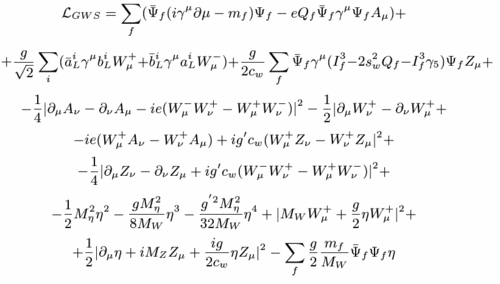





Kommentare (210)