Nein, in diesem Artikel geht es nicht darum, Sudoku-Hefte zu verbrennen. Aber mit etwas Phantasie kann man Sudokus tatsächlich als physikalische Objekte behandeln und dabei etwas über Thermodynamik lernen.
Sudokus sind ja bekanntlich Zahlenrätsel. Auch wenn ihr nie vom Sudoku-Fieber infiziert wart (war ich auch nie, habe nur einige Samurai-Sudoku und eine Handvoll leichter Killer-Sudoku gelöst) kennt ihr vermutlich die Regeln: Man hat ein Raster mit 9×9 Feldern und muss die Ziffern von 1 bis 9 so verteilen, dass in keiner Zeile, Spalte und in keinem Block eine Ziffer doppelt vorkommt. Am Anfang hat man bestimmte Hinweise, nämlich Felder, in denen schon Zahlen drinstehen. So sieht so etwas aus (geklaut von Wikipedia):

Von Wikipit – Eigenes Werk, CC BY-SA 3.0, Link
Und hier ist die Lösung:
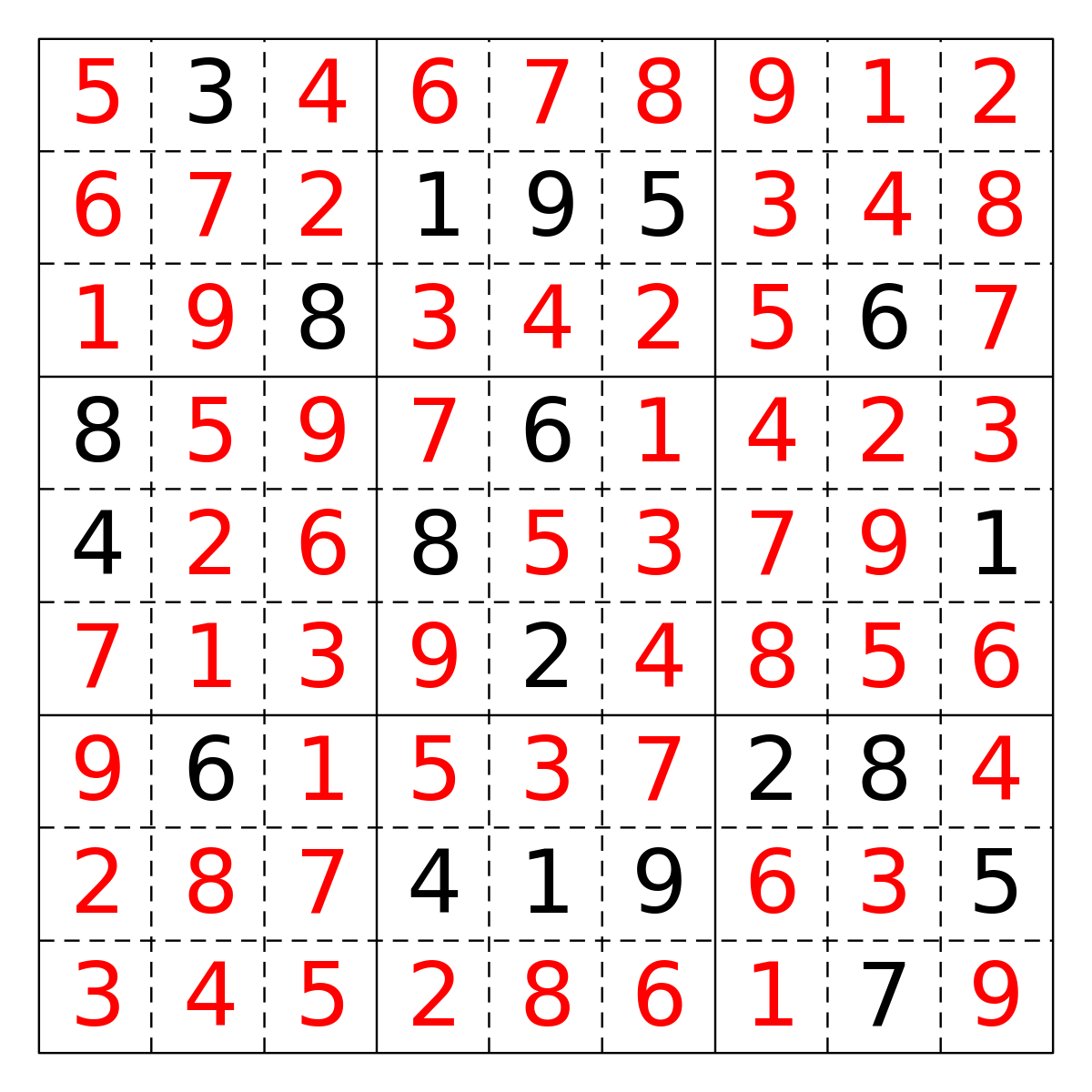
Von Wikipit – Eigenes Werk, CC BY-SA 3.0, Link
Mit Physik hat das erst mal nicht viel zu tun, oder?
Aber PhysikerInnen haben ja manchmal eine seltsame Art zu denken und sehen die Welt auf ihre ganz eigene Weise. Und wenn man ein Sudoku mit PhysikerInnen-Augen ansieht, dann fällt einem vielleicht die Ähnlichkeit zu einigen physikalischen Modellen auf. Genau das haben A. Williams und G. Ackland getan – wobei ich auf den Artikel nur aufmerksam wurde, weil ich mit Graeme Ackland an einem gemeinsamen Projekt beteiligt war und ihn deshalb ein bisschen kenne.
In der Thermodynamik geht es ja darum, wie physikalische Systeme sich bei unterschiedlichen Temperaturen verhalten. Darüber kann man dicke Bücher schreiben (ich empfehle z.B. das von Reif), aber da das hier ein Blog-Eintrag ist, mache ich’s kurz (wobei das natürlich relativ ist, die kürzesten Blogeinträge der Welt schreibe ich ja nicht gerade). Eine etwas längere Einführung in viele thermodynamische Konzepte findet ihr natürlich auch hier auf dem Blog.
Das Grundprinzip hinter der Thermodynamik ist ziemlich simpel: Wir brauchen ein System, das in verschiedenen Zuständen existieren kann. Beispielsweise unser Sudoku: Wir können uns vorstellen, dass jedes der 81 Felder einen der 9 möglichen Werte annehmen kann (die meisten Kombinationen geben aber natürlich kein korrekt gelöstes Sudoku, sondern Unsinn). Damit haben wir dann 81 hoch 9 9 hoch 81 (danke, wereatheist) mögliche Zustände, also immerhin etwa 150 Billiarden (1,5e17) 2 mal 10 hoch 77.
In der Thermodynamik geht es außerdem immer um Temperaturen. Aus dem Alltag wisst ihr schon (auch wenn ihr vielleicht noch nie bewusst darüber nachgedacht habt), dass bei niedrigen Temperaturen Systeme bevorzugt in Zuständen mit niedriger Energie vorliegen. Deshalb gefriert Wasser zu Eis (weil die Eiskristalle energetisch günstig angeordnet sind) oder verdampft bei hoher Temperatur (wobei dann die Bindungskräfte zwischen den Molekülen sehr klein sind, so dass der Energiegehalt steigt). Zur Rolle der Energie habe ich übrigens auch mal was geschrieben.
Temperatur und Energie hängen also irgendwie zusammen. Bevor wir das klären, schauen wir erst einmal, wie man die Energie eines Sudokus definieren kann. Dazu schaut man sich an, wie falsch das Sudoku gelöst ist. Nehmen wir an, das Sudoku ist irgendwie mit Ziffern gefüllt. Klappert jetzt der Reihe nach jedes der 81 Felder ab. Fangen wir links oben an. Jetzt guckt ihr der Reihe nach alle Felder in derselben Zeile (also der obersten) an und jedesmal, wenn dort dieselbe Zahl steht wie im Feld links oben, dann macht ihr einen Strich (Fehler!). Dasselbe tut ihr für alle Felder in derselben Spalte und dann für alle Felder im selben Block. Mit anderen Worten, ihr sucht nach Fehlern – danach, ob diese Zahl, die ihr gerade anguckt, dafür sorgt, dass das Sudoku falsch ausgefüllt wurde. Alle diese Fehlerstriche (für alle 81 Felder) addiert ihr auf. Das ergibt dann eine Gesamtfehlerzahl, die man die Falschheit des Sudoku nennen könnte – aber weil wir Thermodynamik betreiben wollen, nennen wir sie die “Energie”. (Wer spitzfindig ist könnte einwenden, dass wir ja jeden Fehler doppelt zählen – einmal Feld X mit Feld Y, dann nochmal Feld Y mit Feld X. Man könnte alles nochmal durch zwei teilen, um das auszugleichen, aber da es ein konstanter Vorfaktor ist, spielt das hier keine Rolle und wir können das ignorieren.)






Kommentare (10)