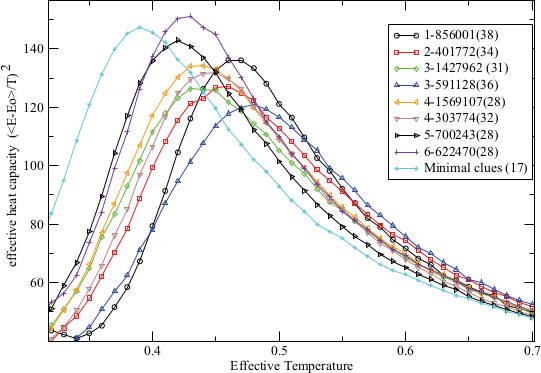
Weil unser Sudoku nun ein physikalisches System geworden ist, so richtig mit Energie und allem, kann man auch seine Eigenschaften angucken. Beispielsweise kann man (im Computer) messen, wie viel Energie das Sudoku schluckt, wenn man die Temperatur erhöht. Das nennt man die Wärmekapazität – genau wie bei normalen Materialien, bei denen man auch Energie reinstecken muss, um die Temperatur zu erhöhen (bei Wasser zum Beispiel eine Kalorie, um ein Gramm um ein Grad zu erwärmen). (Wobei die “Energie” beim Sudoku ja die Zahl der Fehler ist – man guckt sich also an, wie sich die Zahl der Fehler mit der Temperatur ändert und verrechnet das dann zur Wärmekapazität.) Die Wärmekapazität des Sudokus sieht (für unterschiedliche Fälle, also unterschiedliche Hinweiszahlen) so aus:
Aus Williams and Ackland, s.u.
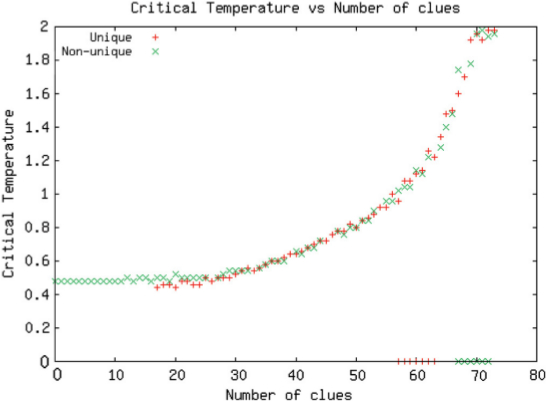
Bei niedrigen Temperaturen ist sie klein, dann steigt sie auf einen Maximalwert an, um dann wieder abzufallen. Die unterschiedlichen Kurven stehen dabei für unterschiedliche Sudokus (also unterschiedliche festgehaltene Hinweisfelder). Tendenziell zeigt sich, dass das Maximum weiter links liegt (also bei niedrigeren Temperaturen), wenn das Sudoku wenige ausgefüllte Hinweisfelder hat (die Zahl in Klammern), und weiter rechts bei vielen ausgefüllten Hinweisfeldern. Das zeigt dieses Bild noch einmal genauer:
Aus Williams and Ackland, s.u.
Wobei hier die kritische Temperatur (also die des Maximums) gegen die Zahl der Hinweise aufgetragen ist. (Die beiden Datenpunktreihen unterscheiden sich darin, dass bei der einen die Lösung eindeutig ist, bei der anderen nicht. Sudokus mit eindeutiger Lösung müssen mindestens 17 Hinweise enthalten.)
Was lernt man nun aus einer solchen Kurve? PhysikerInnen können über das obere Diagramm der Wärmekapazität in Entzücken geraten – es deutet nämlich auf einen Phasenübergang hin. Phasenübergänge kennt ihr alle aus dem Alltag (wenn auch vielleicht nicht unter diesem Namen): Wasser gibt es zum Beispiel in einer flüssigen und einer festen Phase, und wenn man es abkühlt, dann gefriert es irgendwann – das ist genau ein Phasenübergang. Wenn die Kurve der Wärmekapazität einen Knick oder Sprung hat, dann kann man ziemlich sicher sein, dass man es mit einem Phasenübergang zu tun hat. (Anmerkung für die ExpertInnen: Das Maximum ist hier nicht scharf, weil unser Sudoku ja nur eine endliche und ziemlich kleine Größe hat.)
In unserem Sudoku ist die Hochtemperaturphase eine, bei der vergleichsweise viele Fehler im Sudoku sind, so dass die Energie hoch ist. Die Niedrigtemperaturphase (eigentlich sind es zwei, dazu später mehr) ist dagegen eine, bei der die meisten Felder korrekt ausgefüllt sind, es aber an einigen Stellen nicht stimmt. Sudokus (insbesondere schwierige) haben oft scheinbar sehr viele Möglichkeiten, die Felder auszufüllen, und es gibt nur wenige Stellen im Sudoku, an denen es am Ende zu einem Fehler kommt. So eine “Fast-Lösung” kann aber trotzdem ganz anders aussehen als die richtige Lösung – genau das macht Sudokus ja so knifflig (wie wir noch sehen werden, kann man das sogar quantifizieren).
Eine “Fast-Lösung” hat – weil ja die meisten Felder passen – eine niedrige Energie. Um von diesem Zustand mit niedriger Energie zur korrekten Lösung zu kommen, muss man aber sehr viele Felder ändern – tut man dies Schritt für Schritt, wie der hier verwendete Simulationsalgorithmus, so führt der Weg von einem Zustand niedriger Energie zu einem anderen über lauter Zustände mit hoher Energie, die bei niedrigen Temperaturen sehr unwahrscheinlich sind. Das System ist dann in der “Fast-Lösung” gefangen. Weil die Energie hier besonders niedrig ist (wenn auch nicht Null) spricht man auch von einem “lokalen Minimum”.
So etwas gibt es auch in anderen Systemen mit einem Phasenübergang. Eisen beispielsweise wird bei niedrigen Temperaturen (unterhalb 768°C) magnetisch – in der Schule habt ihr vermutlich gelernt, dass es da “Elementarmagnete” gibt (was auch als Modell ganz brauchbar ist). Energetisch am günstigsten wäre es, wenn alle Elementarmagnete überall in dieselbe Richtung zeigen werden, aber beim Abkühlen passiert das normalerweise nicht, weil unterschiedliche Bereiche im Eisen unterschiedliche Ausrichtungen haben. Unser Sudoku benimmt sich also tatsächlich wie ein physikalisches System.






Kommentare (10)