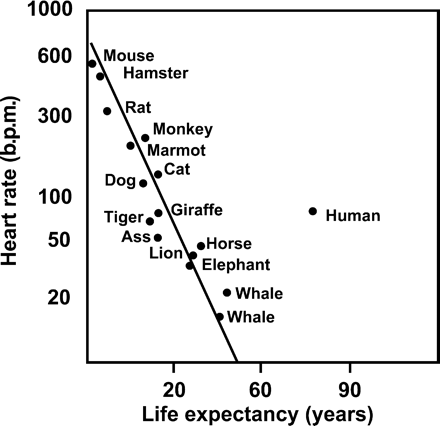
Das Alter von Säugetieren hängt meist mit ihrer Größe zusammen: Große Tiere wie Elefanten werden etwa 70 Jahre alt, Löwen etwa 12-15, kleine Tiere wie Mäuse nur wenige Jahre. Allerdings haben größere Säugetiere auch einen langsameren Stoffwechsel. Die Zahl der Herzschläge im Leben eines Säugetiers ist ungefähr eine Konstante: Egal ob Maus, Löwe oder Elefant, alle leben etwa eine Milliarde Herzschläge lang. Danach müssten wir Menschen mit etwa 20 Jahren sterben, die meisten Menschen, die das Erwachsenenalter erreichen, werden aber wesentlich älter als das.
Hier eine Grafik, die das sehr schön deutlich macht:
(Grafik aus European Heart Journal Supplements)
Wir Menschen leben also ungewöhnlich lange, auch wesentlich länger als zum Beispiel Gorillas, die schwerer sind als wir, aber typischerweise nicht älter als 35-40 Jahre werden. Warum ist das so? Eine mögliche Antwort: Das verdanken wir unseren Großmüttern (oder besser, denen unserer Vorfahren).
Bevor wir uns das genauer angucken, hier gleich vorweg ein Hinweis, um möglicher Verwirrung vorzubeugen: Der Begriff “Lebenserwartung” ist ein bisschen problematisch. Man liest ja z.B. oft, dass die Lebenserwartung im Mittelalter nur bei etwa 30 Jahren lag – das heißt aber nicht, dass es damals nahezu keine Leute gab, die 40 oder 60 wurden, sondern ist einfach der sehr hohe Kindersterblichkeit geschuldet. (Wenn die Hälfte aller Menschen als Kind/Säugling stirbt und die andere Hälfte 60 wird, dann ist die Lebenserwartung eben nur 30 Jahre.) In dem Modell, das ich gleich erkläre, ist dieser Effekt allerdings nicht drin – dort wird eine konstante Sterblichkeit angenommen.
Die Idee der Großmutter-Hypothese (ein Pluspunkt für die Person, die sich das Wort ausgedacht und es korrekt als “Hypothese” bezeichnet hat) besteht darin, dass Menschen ja erst mal eine lange Zeit brauchen, um erwachsen zu werden, dann aber nur eine begrenzte Zeit lang Kinder bekommen können. Solange sich Frauen noch um sehr kleine Kinder kümmern müssen, bekommen sie häufig keine weiteren. Können sie die Pflege der Kinder an andere abgeben, können Frauen früher wieder schwanger werden und so mehr Kinder bekommen. Insgesamt mag es also günstig sein, wenn Frauen insgesamt länger leben und zunächst eigene Kinder bekommen und später dann ihre Enkel großziehen.
Diese Idee kann man durch Computermodelle prüfen, von denen ich hier eins vorstellen will (es gibt noch andere, die zum Teil andere Annahmen machen, aber zu ähnlichen Ergebnissen kommen).
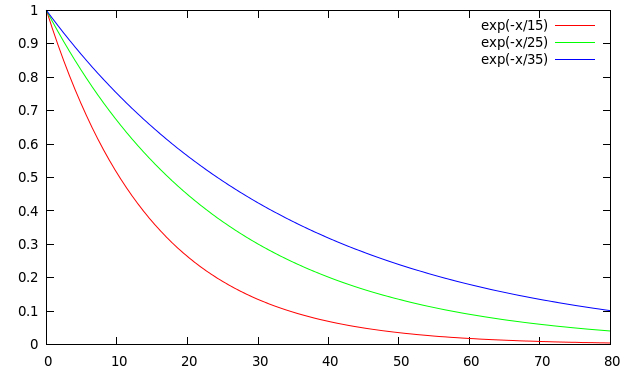
Das Modell nimmt vereinfachend eine konstante Sterblichkeitsrate an. So sieht (wenn ich die Formel richtig umgerechnet habe) die Überlebenswahrscheinlichkeit aus:
Wenn man also mit 1000 Neugeborenen anfängt, dann bleiben nach 20 Jahren nur etwa 250 übrig, wenn die Lebenserwartung 15 Jahre beträgt (rote Kurve), und etwa 600, wenn die Lebenserwartung 35 Jahre beträgt. Ihr seht, dass die Kurve etwas unrealistisch ist, weil zum einen die hohe Säuglingssterblichkeit nicht berücksichtigt wird und zum anderen einige Menschen sehr alt werden können. In der Arbeit werden diese Aspekte auch diskutiert – sie dürften an der zentralen Aussage aber nichts ändern.
Als nächstes muss man sich Gedanken machen, wie das Leben eines einzelnen Menschen (in diesem Fall einer Frau, Männer sind hier nicht so wichtig…) aussieht: Zunächst einmal startet sie als Säugling. Säuglinge sind (weil sie gestillt werden) von der Mutter abhängig und können nicht an Großmütter weitergereicht werden. Danach kommt eine abhängige Kindheitsphase, in der sie gepflegt werden müssen. In dieser Zeit kann eine Frau, die ein solches Kind pflegt, kein weiteres pflegen. (Bei Schimpansenmüttern vergehen z.B. 4 oder 5 Jahre zwischen zwei Geburten – wer mehr darüber wissen will, möge den zeitlosen Klassiker “Wilde Schimpansen” von Jane Goodall lesen.) Es folgt eine unabhängige Jugend, in der noch keine Fortpflanzung möglich ist. Schließlich dann der Eintritt ins Fortpflanzungsfähige Alter, das für Frauen (das ist ein fixer Wert) mit 45 Jahren endet. In dieser Zeit können Frauen Kinder bekommen, wobei die Zeit zwischen möglicher Empfängnis und Geburt auf 1 Jahr festgelegt wurde. (Das umfasst die Zeit, bis die Frau schwanger wird und die Zeit der Schwangerschaft selbst und passt vom Zahlenwert her zu Menschen und Menschenaffen.)
Anschließend können Frauen als Großmütter tätig werden und ihre Enkel versorgen, allerdings nur bis zu einem Alter, bei dem sie zu gebrechlich dafür werden. Anders als in früheren Modellen kann in diesem Modell hier jede Großmutter nur ein einziges Kind versorgen (was sicher eine sehr vorsichtige Annahme ist).
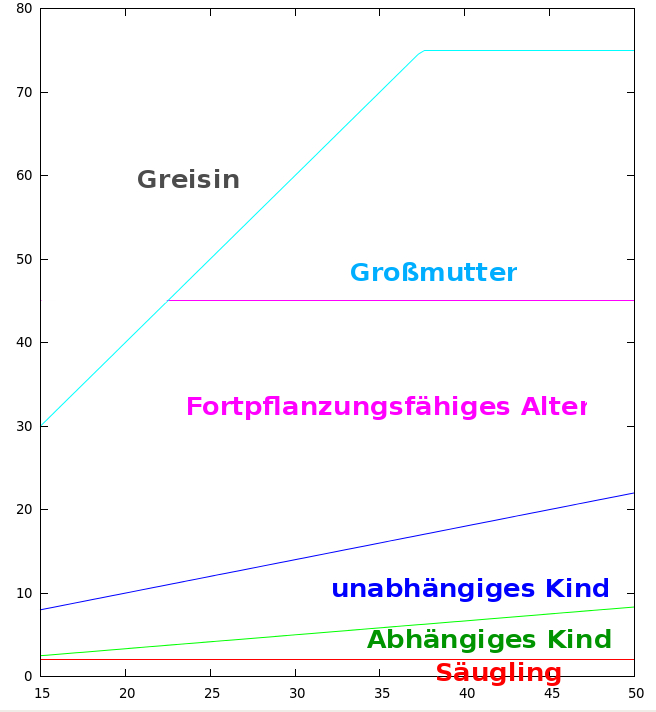
Wie lange die einzelnen Phasen dauern, hängt in diesem Modell von der Lebensdauer ab (also dem Parameter, den ich oben erklärt habe). Weil die Tabellen im paper etwas unübersichtlich sind, habe ich das in einer Grafik zusammengefasst:
Die Säuglingsphase dauert immer zwei Jahre. Je größer die Lebenserwartung ist, desto länger dauert es dann bis zur Unabhängigkeit und zum Erwachsenwerden und bis zum Greisenalter. (Das ist allerdings bei 75 Jahren “gedeckelt”.) Man mag jetzt einwenden, dass natürlich eine längere Lebenserwartung dann auch dadurch getrieben werden könnte, dass eine längere Jugend einen evolutionären Vorteil bietet, das ist hier im Modell aber nicht berücksichtigt worden, hier geht es nur um die Frage, ob Großmütter durch Versorgen von Kindern die Lebensdauer zu größeren Werten verschieben.
Jetzt können wir das System simulieren: Dazu starten wir mit z.B. 1000 Individuen mit bestimmter Lebensdauer und schauen, wie sich die Population Zeitschritt für Zeitschritt entwickelt. Will man das für sehr viele verschiedene Varianten und lange Zeiträume machen, dann wird es allerdings sehr rechenaufwändig. Die AutorInnen der Arbeit waren deshalb schlau, und haben ihr Modell mathematisch in Form von Differentialgleichungen umgeschrieben, die sich deutlich schneller lösen lassen.
Als Ergebnis schaut man sich die Reproduktionsrate an: Wie stark wächst die Population maximal pro Jahr? (Es ist im paper nicht genau erklärt, aber ich gehe davon aus, dass es sich bei der Reproduktionsrate um das Netto-Wachstum handelt, also Zahl der Geburten minus Zahl der Todesfälle.)
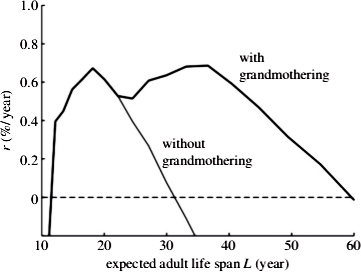
Aus Kim et al, s.u.
Hier ist also aufgetragen um wie viel Prozent die Population pro Jahr wachsen kann. Bei zu kurzer Lebenserwartung wächst die Population nur langsam oder schrumpft sogar – das liegt sicherlich daran, dass dann zwei Jahre bis zum Abstillen sehr lang sind (und hinzu kommt ja noch ein Jahr bis zur nächsten Geburt). Ein Maximum erreicht die Kurve bei einer Lebenserwartung von 18 Jahren, anschließend fällt sie wieder ab. Dieser Abfall liegt laut dem paper am zunehmenden Alter bei der ersten Geburt – ich denke, dass hier auch hinzukommt, dass immer mehr Frauen die 45-Jahre-Grenze erreichen, ab der sie keine Kinder mehr bekommen können. Einen Großmutter-Effekt gibt es hier noch nicht, weil das Minimum-Alter fürs “großmuttern” von 45 Jahren noch oberhalb der Schwelle zum Greisinnenalter liegt. (Was mir aus dem paper nicht ganz klar wird, ist, ob bei dieser Lebenserwartung von z.B. 20 Jahren eine Frau über 40 – die ja schon Greisin ist – noch Kinder bekommen kann.)
Ab einer Lebenserwartung von 22,5 Jahren können dann Frauen über 45 als Großmütter agieren (sie dürfen ein einmal übernommenes Kind auch weiter betreuen, selbst wenn sie das Greisinnen-Alter erreichen). Und hier sieht man dann sofort einen drastischen Effekt durch das Wirken der Großmütter: Die Kurve mit Großmutter-Efekt schnellt wieder nach oben und erreicht ein zweites Maximum bei einem Alter von 37 Jahren und auch bei sehr hoher Lebenserwartung bleibt die Reproduktionsrate positiv. Es zeigt sich also ein deutlicher Großmutter-Effekt.
Aber kann ein solcher Großmutter-Effekt sich auch evolutionär durchsetzen? Um das zu prüfen, wurde zusätzlich Evolution eingebaut: Jedes Kind bekommt zunächst als Lebenserwartungsparameter den Mittelwert aus den Parametern der Eltern, doch dieser Wert kann durch Mutation noch nach oben oder unten verschoben werden. Weiterhin wurde angenommen, dass der Lebensraum der betrachteten Gruppe Platz für maximal 1000 Menschen liefert. Wenn es mehr als 1000 Menschen gibt, dann sterben im nächsten Simulationszeitraum (typischerweise 3 Monate) so viele Menschen zufällig, dass die Zahl 1000 wieder erreicht wird.
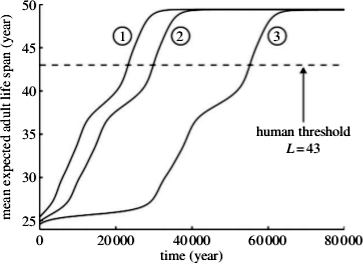
Das Evolutionsmodell liefert folgende Kurven:
Aus Kim et al, s.u.
Man sieht, wie sich die Lebenserwartung von einem niedrigen Anfangswert evolutionär nach oben entwickelt. Es gibt einen Knick der Kurve bei 37,5 Jahren, der sicherlich etwas mit dem Übertritt ins Greisinnenalter zu tun hat (siehe das erste Bild). Die drei eingezeichneten Kurven unterscheiden sich darin, welche Annahmen über die Männer im Modell gemacht wurden. Ja, die sind zwar nicht so wichtig, wenn es um Fortpflanzung geht, aber ein bisschen tragen sie ja doch bei 😉 . Es wurde angenommen, dass Männer, die eine kürzere Lebenserwartung haben, tendenziell attraktiver sind als Männer, die länger leben. Als Begründung wird auf eine Arbeit aus dem Jahr 1957 verwiesen, die ich nicht gelesen habe. Bei Kurve 1 ist dieser Effekt schwach, bei Kurve 3 ist er sehr stark, entsprechend dauert es (weil ja die erfolgreicheren jung sterbenden Männer sich dann stärker durchsetzen können) ziemlich lange, bis sich der Großmutter-Effekt gegen den gegenteiligen Effekt (den “Draufgänger-Effekt”?) durchsetzt. Erhöht man den “Draufgänger”-Effekt noch weiter, dann kann sich das Großmuttern nicht mehr evolutionär durchsetzen und die Lebenserwartung bleibt niedrig.
Das paper (und vor allem das “supplementary material”) enthält noch ein paar weitere Variationen und diskutiert verschiedene Effekte, aber das wird mir jetzt ehrlich gesagt zu speziell, insbesondere, weil es hier ja nur um ein bestimmtes Modell geht und andere Modellannahmen sicher zu anderen Zahlenwerten führen. Die generelle Idee der Großmutter-Hypothese wird aber durch das Modell deutlich gestützt. Es ist also tatsächlich plausibel, dass eine Änderung des Sozialverhaltens bei den Urzeit-Großmüttern dazu geführt hat, dass wir Menschen eine deutlich höhere Lebenserwartung haben, als eigentlich zu erwarten wäre.
Das Originalpaper ist:
Peter S. Kim, James E. Coxworth and Kristen Hawkes
Increased longevity evolves from grandmothering
Proc. R. Soc. B published online 24 doi: 10.1098/rspb.2012.1751
“Data Supplement” https://rspb.royalsocietypublishing.org/content/suppl/2012/10/18/rspb.2012.1751.DC1.html
Es ist nicht einfach zu lesen, weil zumindest für den Laien wie mich viele Dinge nicht sehr genau erklärt sind und insbesondere, weil die Informationen, wie das Modell genau funktioniert, zwischen paper und Supplement aufgespalten sind und die Unterschiede der beiden Modelle mit und ohne Evolution nicht sauber aufgelistet sind.






Kommentare (15)