Im zweiten Teil der Quantenmechanik-Reihe schauen wir uns die Zustände eines Teilchens noch etwas genauer an.
Was ist ein Zustand?
Bisher habe ich immer nur von Teilchen gesprochen, die irgendwo sind (oder manchmal auch irgendwo nicht sind). Der Zustand eines Teilchens war also immer durch seinen Ort gekennzeichnet. Im klassischen Fall war der Ort eindeutig, in der QM konnte der Zustand aber eine Überlagerung verschiedener Orte sein. Wenn ich das Teilchen an einem Ort messe, dann ist es hinterher in dem entsprechenden Zustand.
Nicht alle Zustände sind aber Ortszustände (obwohl das Teilchen natürlich immer irgendwo sein muss). Man kann ja auch andere Eigenschaften von Teilchen messen – dann sind sie hinterher ebenfalls in einem bestimmten Zustand, aber dieser Zustand ist nicht unbedingt einer mit einem eindeutigen Ort. Ging das zu schnell? Keine Sorge, wie das genau geht, schauen wir uns jetzt an.
Dazu betrachten wir ein (hier etwas vereinfachtes) Beispiel, nämlich das einfachste denkbare Molekül.
Dazu brauchen wir zunächst mal ein Wasserstoffatom. Das besteht aus einem Proton und einem Elektron. Das Proton ist knapp 2000 mal schwerer als das Elektron und ich tue hier so, als wäre es unendlich schwer und müsste nicht mit den Mitteln der Qm beschrieben werden. Wir müssen uns also nur um das Elektron kümmern. Das Elektron ist elektrisch negativ geladen und wird vom Proton angezogen. Es nähert sich deshalb dem Proton an und hält sich bevorzugt in seiner Nähe auf. Im Zustand mit der niedrigsten Energie sieht seine Wellenfunktion etwa so aus:
Dabei habe ich den Wert der Wellenfunktion entlang einer Linie aufgetragen, die durch das Proton geht. (Es gibt auch dreidimensionale Darstellungen, aber dann wird das, was gleich kommt, sehr unübersichtlich.) Da, wo die Funktion ihr Maximum hat, sitzt genau das Proton. Das Elektron ist also bevorzugt dicht ans Proton gekuschelt (seine Wahrscheinlichkeit ist dort besonders hoch), aber auch nicht zu dicht.
Aber keine Sorge, wir brauchen uns um die Details der Wellenfunktion im Moment nicht zu kümmern (die Bilder hier sind eh nur qualitativ richtig). Solange das Elektron im energetisch günstigsten Zustand (dem Grundzustand) ist, hält es sich möglichst dicht am Proton auf, das ist eigentlich alles, was uns im Moment interessiert. Wir haben also einen Zustand des Elektrons, nämlich den Grundzustand an diesem Proton.
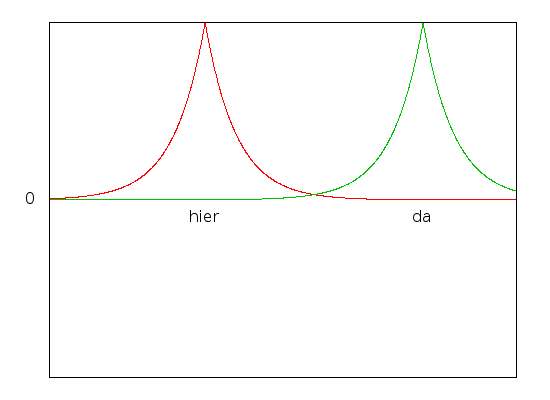
Jetzt bringen wir ein zweites Proton ins Spiel. Nehmen wir erstmal an, das Proton wäre sehr weit vom ersten weg. Unser Elektron kann jetzt entweder beim Proton “hier” sein oder beim Proton “da”:
Wir könnten das messen, indem wir z.B. die elektrische Ladung messen – ist das Elektron beim Proton “hier”, dann haben wir “hier” ein neutrales Wasserstoffatom und “da” ein geladenes Proton. Das ist also genau die Situation vom letzten Mal, bei der wir ja mit zwei Zuständen |hier> und |da> angefangen haben.
Wir haben beim letzten Mal auch gesehen, dass wir beliebige Misch-Zustände aus |hier> und |da> haben können – der allgemeine Zustand ist
a|hier> + b |da> mit der Bedingung a²+b²=1.
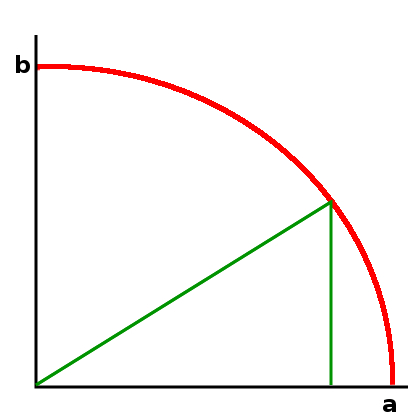
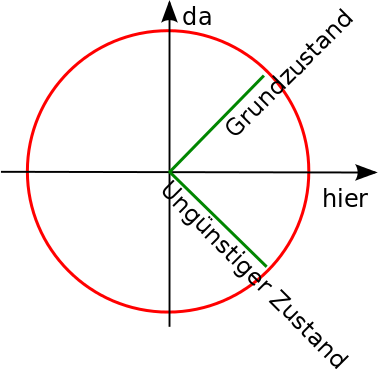
Grafisch habe ich das mit diesem Bild veranschaulicht:
Dahinter steckt übrigens – falls ihr es nicht gemerkt habt – der Satz des Pythagoras: Das eingezeichnete grüne Dreieck ist ja rechtwinklig, und ihr habt sicher mal die Formel a²+b²=c² lernen (und vielleicht auch beweisen) müssen. Die Länge c ist hier gerade gleich 1, weil die Summe unserer Wahrscheinlichkeiten ja 1 sein soll.
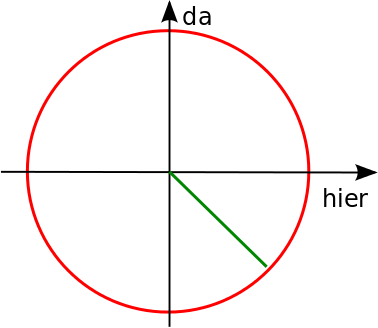
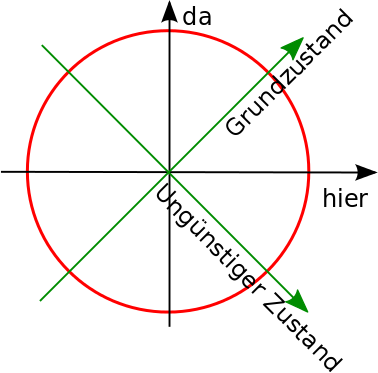
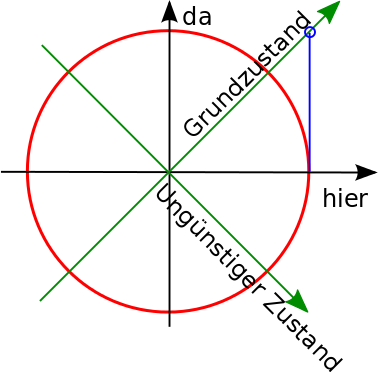
Dabei war ich zugegebenermaßen etwas schlampig, denn a und b können auch negativ sein. Eigentlich müsste das Bild also so aussehen (diesmal mit inkscape statt gimp gezeichnet, das muss ich eh mal lernen):
Dabei habe ich die Achsen jetzt mit “hier” und “da” beschriftet, nicht mit den Zeichen für die Koeffizienten, weil das dann später übersichtlicher wird, wenn wir noch mehr Achsen einführen.
Kleine Aufgabe: welchen Zustand habe ich in grün oben eingezeichnet?
Antwort: Der Zustand liegt unter 45°, also ist der Anteil von “hier” und “da” gleich groß, der “da”-Anteil ist aber negativ (er geht ja nach unten). Der Zustand ist also
Das ist auch ein erlaubter Zustand, denn beim Quadrieren fällt das Minuszeichen ja weg.
Unser Elektron kann also in einem beliebigen Mischzustand zwischen |hier> und |da> sein, so wie bisher auch.
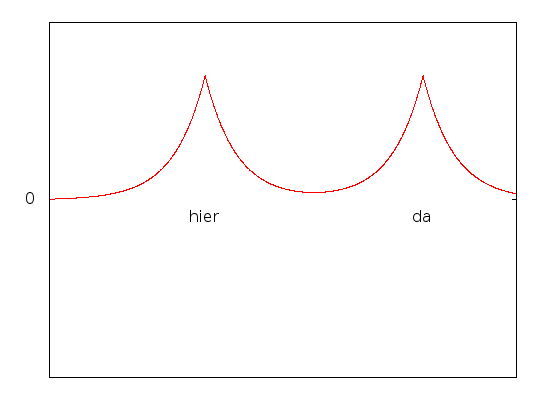
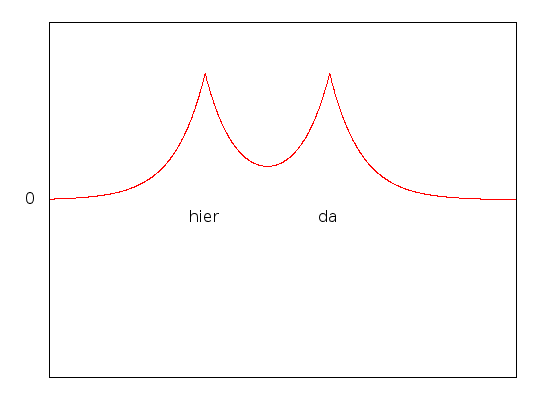
Interessant wird die Sache, wenn wir unsere beiden Protonen einander annähern. Dann ist es für das Elektron energetisch günstiger, sich in der Mitte zwischen den beiden Protonen aufzuhalten als weiter außen, weil sich dort die elektrische Anziehung der beiden Protonen überlagert. Der energetisch günstigste Zustand ist der, bei dem die beiden Zustände addiert werden:
Dieser Zustand ist der Grundzustand, also der mit der niedrigsten Energie. Die zugehörige Wellenfunktion sieht etwa so aus:
Wie ihr seht, ist sie in der Mitte zwischen den Protonen etwas größer geworden, so dass das Elektron das elektrische Feld sozusagen gut ausnutzt. Der Effekt wird noch stärker, wenn wir die beiden Protonen dichter zusammenrücken lassen:
Allerdings sollten die beiden Protonen auch nicht zu eng zusammenrücken – denn sie sind ja positiv geladen und stoßen sich ab. Es gibt also irgendwo einen besonders günstigen Abstand der beiden Protonen, und nur den betrachten wir jetzt. Dank unseres Elektrons sind die Protonen jetzt aneinander gebunden, weil ja die Energie der beiden protonen kleiner ist, wenn sie zusammen sind, als wen sie es nicht sind. Wir haben ein ganz einfaches Molekül gebaut, das aus zwei Protonen und einem Elektron besteht. Da ein Elektron und ein Proton zusammen ein Wasserstoff-Atom bilden, haben wir also zwei Wasserstoffatome verbunden, allerdings fehlt ein Elektron, Was wir gebaut haben ist ein H2+-Molekül. (Nebenbei habt ihr also gleich gesehen, wie man chemische Bindungen mit Hilfe der Quantenmechanik verstehen kann – eigentlich wollte ich das gar nicht erklären…)
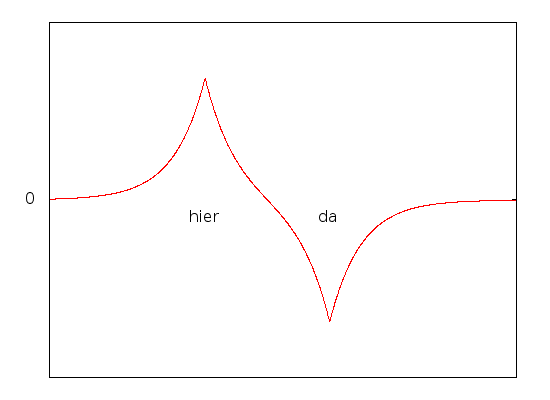
Umgekehrt gibt es auch einen energetisch besonders ungünstigen Zustand (das ist auch genau der, den ich oben für die Aufgabe gezeichnet hatte)
Hier sieht die Wellenfunktion etwa so aus:
und die Wahrscheinlichkeit, das Elektron da zu treffen wo es energetisch günstig ist (nämlich zwischen den Protonen) ist besonders klein.
(Kleine Anmerkung: Natürlich gibt es noch andere Zustände des Elektrons, bei denen die Wellenfunktion anders aussieht, die betrachte ich hier aber nicht. Ich beschränke mich auf die Kombination des “hier”- und des “da”-Zustands.)
Wir können diese beiden Zustände in unser Diagramm einzeichnen:
Statt “hier” und “da” als Achsen zu nehmen, könnten wir genauso gut die beiden Energie-Zustände als Achsen nehmen:
Wie ihr seht, können wir auch umgekehrt den Zustand |hier> über die beiden anderen Zustände ausdrücken:
Kleine Übung: Wie wird der Zustand |da> ausgedrückt?
Antwort:
Ihr könnt einen beliebigen Zustand also auf zwei unterschiedliche Arten hinschreiben: Entweder als Überlagerung aus |hier> und |da> oder als Überlagerung aus |Grundzustand> und |ungünstiger Zustand> – jeder Punkt auf der Kreislinie kann entweder in der einen oder der anderen Weise ausgedrückt werden.
Aufgabe: Könnt ihr einen beliebigen Zustand auch über eine Kombination von |da> und |Grundzustand> ausdrücken? Versucht es als Beispiel mit dem Zustand |hier>.
Antwort: Ja, das geht, es ist aber ein bisschen trickreich.
Ihr könnt den “hier”-Zustand erreichen, wenn ihr erst auf der Grundzustands-Linie bis zum blauen Kringel geht und dann von dort aus senkrecht nach unten. Mathematisch bekommt ihr den Zustand durch
Macht euch keine Sorgen, wenn ihr das nicht auf die Schnelle ausrechnen konntet, es gehört ein bisschen Übung dazu, auch wenn es nicht wirklich schwer ist: In der Grafik hat der Zustand “hier” die Koordinaten (1,0), der Zustand “da” die Koordinaten (0,1) und der “Grundzustand” die Koordinaten (1/√2, 1/√2). Ihr müsst jetzt Zahlen finden, so dass der Grundzustand und der da-Zustand mit diesen Zahlen multipliziert und dann addiert gerade (1,0) ergeben. Um den zweiten Koordinatenwert auf Null zu bekommen, muss der Faktor des “da”-Zustands um √2 größer sein als der Faktor des Grundzustands (und die beiden müssen umgekehrtes Vorzeichen haben), außerdem muss der Faktor des Grundzustands gleich √2 sein, damit für die erste Koordinate 1 herauskommt. Die rechnerei ist aber hier wirklich nicht das entscheidende.
Wichtiger ist, dass das Ergebnis sehr merkwürdig ist: Der Faktor vor dem Grundzustand ist größer als 1. Das Quadrat dieses Faktors kann also nicht die Wahrscheinlichkeit angeben, das Teilchen im Grundzustand zu finden (Wahrscheinlichkeiten größer 1 ergeben nicht viel Sinn). Das hat einen einfachen Grund: Die beiden Zustände |da> und |Grundzustand> stehen im Bild nicht senkrecht aufeinander. Physikalisch bedeutet das, dass ein Teilchen, das im |Grundzustand> ist, auch eine Amplitude dafür hat, im Zustand |da> zu sein.Das macht das Rechnen mit solchen Kombinationen von Zuständen sehr unpraktisch. Messe ich zum Beispiel das Teilchen im Zustand |da> (a=1), dann ist es eben nicht so, dass es jetzt eindeutig nicht im |Grundzustand> ist (es ist also nicht b=0), denn der Grundzustand hat ja auch einen Anteil des da-Zustands.
Weil das die Sache unnötig verkompliziert, verwendet man eigentlich immer solche Sätze von Zuständen, die sich gegenseitig ausschließen – wenn ein Teilchen hier ist, ist es auf keinen Fall da, wenn es im Grundzustand ist, ist es auf keinen Fall im ungünstigen Zustand. In der mathematischen Fachsprache sagt man übrigens, dass ein solcher Satz von Zuständen, über den ich einen beliebigen Zustand bequem ausdrücken kann, eine orthonormale Basis bildet. (Nicht “Ottonormal”, sondern “ortho”-“normal”. “Ortho”, weil die Zustände senkrecht zueinander sind (wie im Wort “othogonal”), und “normal”, weil die Zustände die “Länge” 1 in unserem Diagramm haben. Ist aber nur Mathe-Sprech.) |hier> und |da> zusammen sind also eine Basis, |Grundzustand> und |ungünstiger Zustand> zusammen sind eine andere.
Falls ihr das wirr findet, hier noch eine ähnliche Situation im Alltag: Im Straßennetz von Manhattan sind die Straßen ja alle brav rechtwinklig zueinander angeordnet. Ich kann deswegen beispielsweise sagen “Wir treffen uns an der Kreuzung 48. Straße und 5th Avenue”, und das ist ganz eindeutig. Ich kann natürlich genausogut die Koordinaten aus meinem GPS-Empfänger (wenn ich einen hätte) angeben und sagen: “Die GPS-Koordinaten sind 40°45Minuten 21Sekunden Nördlicher Breite und 73° 58Minuten 45 Sekunden westlicher Länge” (ich hoffe, ich habe das mit dieser Seite hier richtig ausgeknobelt.) Es wäre aber unpraktisch, die Angaben zu mischen und z.B. zu sagen “an der Kreuzung 5th Avenue mit dem 73-ten Längengrad”.
Das wichtige Fazit hier ist also: Es gibt unterschiedliche Möglichkeiten, denselben Zustand darzustellen. Warum das so wichtig ist, das sehen wir als nächstes.
Eigenzustände
Nehmen wir an, unser Elektron wäre tatsächlich im Grundzustand. Wenn ich jetzt mit einem geeigneten Apparat die Energie des Systems messe, dann bekomme ich einen bestimmten Wert, eben den der Grundzustandsenergie. Weil ich den Zustand jetzt gemessen habe, weiß ich sicher, dass das Elektron jetzt tatsächlich im Grundzustand ist.
Was passiert, wenn ich nun als nächstes den Ort messe? Mit den Überlegungen vom letzten Mal solltet ihr in der Lage sein, das selbst herauszuknobeln.
Antwort: Der Grundzustand ist ja
Die beiden Zustände |hier> und |da> haben also dieselbe Amplitude. Die Wahrscheinlichkeit, das Elektron an einem der beiden Orte zu messen, ist jeweils das Quadrat der Amplitude, also genau 1/2. Wenn ich also das Elektron im Grundzustand habe und messe dann den Ort, dann messe ich das Elektron in 50% der Fälle hier und in 50% der Fälle da.
Nehmen wir an, ich hätte das Elektron “da” gemessen. Was passiert, wenn ich jetzt als nächstes wieder die Energie messe?
Antwort: Der Zustand “da” ist ja
ich habe jetzt also eine 50%-Wahrscheinlichkeit, das Elektron wieder im Grundzustand zu finden und eine 50%-Wahrscheinlichkeit, es im ungünstigen Zustand zu finden. (Das verletzt übrigens nicht die Energieerhaltung. Grob gesagt liegt das daran, dass bei der Messung des Ortes Energie mit der Umgebung ausgetauscht wird.)
Man kann also sagen: Ist das System in einem der Ortszustände, dann ist seine Energie nicht eindeutig, ist es in einem der Energiezustände, ist sein Ort nicht eindeutig.Messe ich erst die eine, dann die anderen Messgröße, dann ändert das System jeweils seinen Zustand.
Als besondere Sprechweise hat sich hier (auch im Englischen) der Wortzusatz “eigen-” eingebürgert: Die Zustände |hier> und |da> sind “Eigenzustände” des Ortes (“eigenstates” im Englischen), die Zustände |Grundzustand> und |ungünstiger Zustand> sind Eigenzustände der Energie.
In unserem Beispiel hier kann das Elektron nicht gleichzeitig in einem Eigenzustand des Ortes und der Energie sein. Dies ist der entscheidende Unterschied zwischen QM und klassischer Physik: In der klassischen Physik hat ein Teilchen immer einen eindeutigen Ort und eine eindeutige Energie, in der Qm ist das nicht notwendigerweise der Fall.
Aus all diesen Überlegungen könnt ihr noch etwas anderes sehen: Diese ganze Kombiniererei von Zuständen funktioniert nur deswegen so, weil wir im Zweifel auch einen Zustand mit einem negativen Koeffizienten versehen dürfen, beispielsweise, als wir “da” über die beiden Energiezustände ausgedrückt haben. In den Kommentaren zum ersten Teil haben einige von euch ja gefragt, warum die Vorfaktoren an den Zuständen nicht selbst Wahrscheinlichkeiten sind, sondern warum man sie erst quadrieren muss. Hier seht ihr, dass das ganze mit Wahrscheinlichkeiten statt Wahrscheinlichkeitsamplituden so nicht klappen würde, denn Wahrscheinlichkeiten können nicht negativ sein. (Gut, es gibt einen Artikel von Feynman, in dem er sich mit negativen Wahrscheinlichkeiten beschäftigt hat in der Hoffnung, damit ein paar Probleme in der Quantentheorie elegant lösen zu können – es hat aber am Ende nicht geklappt.)
Die Besonderheit der Energieeigenzustände
Auch wenn es eigentlich nicht zentral ist, um Dinge wie Verschränkung zu verstehen, will ich doch noch kurz eine besondere Eigenschaft der Energieeigenzustände erläutern: Sie sind zeitlich stabil. Wenn ihr das Elektron in den |Grundzustand> versetzt, dann bleibt es dort für alle zeit. Auch ein Elektron im |Ungünstigen Zustand> würde – ohne jede äußere Störung – dort für immer bleiben. Real gibt es aber immer Störeinflüsse aus der Außenwelt, die dazu führen würden, dass das Elektron in den energetisch günstigeren Zustand fällt und seine Energie abgibt, deswegen sind höherenergetische Zustände normalerweise nicht stabil.
Mit Zuständen wie |hier> und |da> ist das anders. Versetzt ein Teilchen in den Zustand |hier>, dann wird sich der Zustand mit der Zeit ändern – es wird in einem Mischzustand aus |hier> und |da> geraten, dann irgendwann ist es |da> und dann geht es über einen Mischzustand wieder zurück nach |hier>. Schreibt man den Zustand als
dann ändern sich die Werte von a und b also mit der Zeit. Den genauen zeitlichen Verlauf kann man berechnen – dazu dient die berühmte Schrödingergleichung. Das Hin- und Herschwappen der Wellenfunktion zwischen unterschiedliche Zuständen habe ich übrigens auch in meiner Schrödingergleichungs-Serie mal erklärt, sogar mit ein paar netten Animationen (Ja, klickt den Werbelink (ka-cheng)!!!)
Achtung: Ihr dürft nicht annehmen, dass der Mischzustand aus |hier> und |da> zwischendurch gerade einer der Energie-Eigenzustände ist – das ist er nicht. bei dem Mischzustand, der durch die Zeitentwicklung aus dem |da>-Zustand entsteht, sind die Koeffizienten komplexe Zahlen. Diese Extra-Komplikation ist aber für den Hauptteil nicht so wichtig, deswegen verbanne ich sie hinter dies Warnschild.
Wie lange ein solcher Schwapp-Vorgang dauert, hängt vom Energieunterschied zwischen dem Grundzustand und dem ungünstigen Zustand ab: Je kleiner dieser Energieunterschied ist, desto länger dauert das Schwappen. (Und der Energieunterschied hängt wiederum daran, wie stark sich die beiden Wellenfunktionen “hier” und “da” oben im Bild überlappen – in der Fachsprache nennt man das auch ganz anschaulich das “Überlapp-Integral”.) Habe ich also zwei Protonen, die weit entfernt sind, und ein Elektron beim Proton “hier”, dann wird es sehr lange dauern, bis es sich beim Proton “da” befindet, so dass es für mich so aussieht, als wäre das Elektron einfach “hier”. Das entspricht auch unserer Alltagserfahrung: Die Eigenschaften von Atomen ändern sich nicht plötzlich, nur weil irgendwo im Universum ein einsames Proton rumschwebt – wenn ständig Elektronen aus unserem Körper zu weit entfernten Protonen rüberschwappen würden, wäre das vermutlich auch nicht so super-gesund.
Der Quanten-Zeno-Effekt
Stellt euch vor, ihr habt ein System in einem Zustand, der sich mit der Zeit ändert (der also, in der Fachsprache, die wir jetzt kennen, kein Energie-Eigenzustand ist, sondern eine Überlagerung aus unterschiedlichen Energie-Eigenzuständen). Ein Beispiel wäre der “hier”-Zustand unseres Elektrons zwischen den beiden Protonen, der sich ja – sich selbst überlassen – langsam zeitlich ändert und zum “da”-Zustand wird.
Nehmt an, ihr hättet das Elektron gerade jetzt im Zustand “hier” gemessen. Einen Moment später hat sich der Zustand dann geändert, er ist jetzt eine Überlagerung von “hier” und “da”:
Kurz nach der ersten Messung wird der Wert von a nahezu gleich 1 sein und der Wert von b noch sehr klein. Wenn ihr also eine weitere Ortsmessung macht, dann werdet ihr das Teilchen ziemlich sicher wieder “hier” finden. Und wenn ihr dann noch eine Ortsmessung macht, gilt wieder das gleiche. Macht ihr also ganz viele Ortsmessungen direkt hintereinander, dann könnt ihr das Teilchen mit sehr hoher Wahrscheinlichkeit im “hier”-Zustand festnageln. Das Teilchen kann sich also nicht aus dem Zustand wegbewegen.
Das erinnert ein bisschen an das Zeno-Paradoxon: Zeno war ein griechischer Philosoph, der versucht hat zu beweisen, dass es keine Bewegung geben kann. Einer seiner Beweise beruhte darauf, dass man, um von A nach B zu kommen, ja erst mal die halbe Strecke von A nach B gehen muss, und davon erst mal wieder die halbe Strecke – also schlussendlich unendlich viele (wenn auch winzige) Strecken gehen muss, also kommt man nie von A nach B. (Mit den Mitteln der modernen Mathematik sieht man schnell, dass die unendlich vielen unendlich winzigen Strecken in der Summe ja nur endlich sind und in endlicher Zeit zurückgelegt werden können.)
Bei unserem Elektron ist es ähnlich: Um vom “hier”-Zustand zum “da”-Zustand zu kommen (bei dem also a=0 und b=1) ist, muss es erst mal zum Zwischenzustand kommen. Und vorher erst mal zu einem, wo b noch sehr klein ist. Weil wir das System durch das ständige Messen aber daran hindern, kann es den Zustand “hier” (fast) nie verlassen. (“Fast” deshalb, weil es natürlich eine gewisse Wahrscheinlichkeit gibt – auch wenn b² sehr klein ist, ist es ja nach einem kleinen Moment nicht Null.) Man spricht deswegen auch vom Quanten-Zeno-Effekt. Weil man am Quanten-Zeno-Effekt ziemlich gut sehen kann, wie quantenmechanische Messungen genau funktionieren (Fragen wie “Was genau ist eine Messung”, “wie lange muss eine Messung dauern” etc. sind immer noch nicht vollständig geklärt), hat man sich viel Mühe gegeben, ihn auch experimentell umzusetzen.
Wie ihr seht, habt ihr – wenn ihr bis hierher durchgehalten habt – schon genügend Wissen angesammelt, um tatsächlich einen echten in der Forschung heiß diskutierten Quanteneffekt verstehen zu können, und zwar nicht mit irgednwelchen dubiosen Analogien, sondern genau so, wie es auch PhysikerInnen tun. Gar nicht so schlecht, oder?
Tja, eigentlich wollte ich jetzt noch das wichtige Beispiel Polarisation erklären – aber wie üblich ist dieser Teil mal wieder vieeel länger geworden als gedacht. Die Polarisation vertage ich also aufs nächste Mal, dann ist es aber auch nicht mehr weit bis zur Verschränkung – versprochen.









Kommentare (53)