Quantenmechanik verstehen III – Verschränkung

Von MartinB / 27. Januar 2013 / 122 Kommentare

Heute ist es endlich so weit: Wir gucken uns an, wie die berühmte quantenmechanische Verschränkung funktioniert.

Ein anderes Beispiel: Polarisation

Viele Experimente zur Quantenmechanik macht man mit Photonen, also den “Teilchen des Lichts”. (Fragt drei PhysikerInnen nach der genauen Definition eines Photons, und ihr bekommt vermutlich vier verschiedene Antworten, deswegen setze ich die Erklärung mit den Lichtteilchen in Anführungsstriche. Der berühmte Physiker Lamb hat sogar mal einen Artikel mit dem Titel “Anti-Photon” geschrieben, in dem er schreibt “Only a comedy of errors and historical accidents led to its popularity among physicists and optical scientists. ” Aber keine Sorge, euch können diese Feinheiten hier erstmal egal sein, irgendwann schreibe ich auch darüber mal was (das gehört ja eigentlich in die momentan in Warteschleife liegende Quantenfeldtheorie-Serie)…)

Ja, also zurück zu den Photonen. Wir machen uns das Leben hier einfach und betrachten eine Lichtquelle, die sehr schwaches Licht aussendet. Lässt man dieses Licht auf einen Sensor fallen und misst die Energie, dann stellt man fest, dass die Energie quantisiert ist – die Energie kommt in Paketen, deren Größe von der Lichtwellenlänge abhängt: Je kleiner die Wellenlänge, desto größer die Energie eines Pakets. (Das ist übrigens auch der Grund, warum ihr mit wenig UV-Strahlung einen Sonnenbrand bekommen könnt, mit beliebig viel sichtbarem Licht aber nicht: Die Energiepakete des sichtbaren Lichts reichen nicht aus, um die Haut zu schädigen.) Für diese Erklärung (also die der Energiepakete, nicht das mit dem Sonnenbrand) hat Einstein übrigens seinen Nobelpreis bekommen.

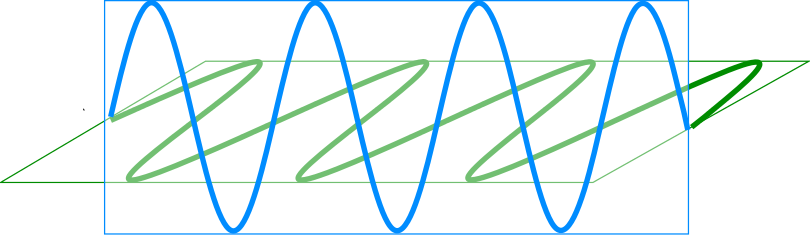
Mich interessiert hier aber eine andere Eigenschaft der Photonen, nämlich ihre Polarisation. Photonen sind ja die Teilchen, aus denen elektromagnetische Wellen bestehen. (Das ist seehr salopp gesagt – in eine rkohärenten elektromagnetischen Welle ist die Zahl der Photonen nicht mal genau definiert, das darf euch hier aber egal sein) Das elektrische Feld schwingt dabei senkrecht zur Richtung, in der sich das Licht ausbreitet (wenn ihr gern toll klingende Fachwörter mögt: Man nennt das eine “Transversalwelle”). Nehmt an, das Licht fliegt entlang einer bestimmten Achse (im Bild nach rechts), dann ist die Schwingungsrichtungrichtung des elektrischen Feldes nach oben/unten (blau) oder nach vorn/hinten (grün):

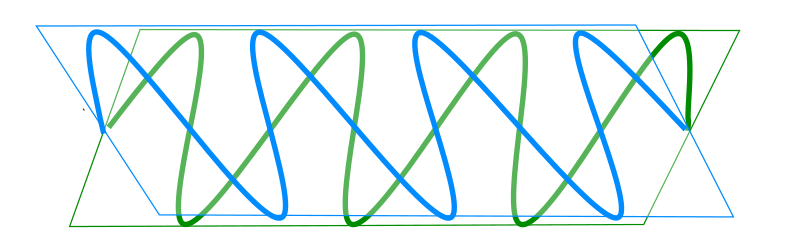
Das Photon kann auch unter einem Winkel polarisiert sein, beispielsweise unter 45° nach schräg vorn oder schräg hinten (ich hoffe, die Perspektive ist einigermaßen zu erkennen):

Man kann die Polarisation eines Photons also über einen Winkel angeben – da das elektrische Feld immer senkrecht zur Ausbreitungsrichtung ist, kann man beispielsweise sagen: Ein Photon ist senkrecht polarisiert, oder waagerecht, oder unter einem Winkel von 45°. Die zugehörigen Zustände schreibe ich hier mit kleinen Pfeilen, weil das schön anschaulich ist:

Senkrecht polarisiert $|\uparrow\rangle$ ,
waagerecht polarisiert $|\rightarrow\rangle$ ,
unter -45° $|\nearrow\rangle$ und
unter +45° $|\nwarrow\rangle$ (wobei ich die mathematische Konvention benutze, dass Winkel gegen den Uhrzeigersin positiv gezählt werden, das spielt aber keine Rolle, weil wir gleich nur die Pfeile angucken werden – übrigens haben wir jetzt echtes LaTeX hier auf dem Blog, Wunder der Technik…).

Anmerkung für die ganz Genauen: Ich betrachte hier nur sogenannte lineare Polarisation. Es gibt auch zirkular polarisiertes Licht – das könnten wir mit unserem angehäuften Wissen auch verstehen, wir brauchen es hier aber nicht – Verschränkung ist ja im Moment unser Ziel.

Polarisationen kann man leicht messen: Dazu schickt man ein Photon durch einen Polfilter. Ein Polfilter hat auch eine Richtung, genau wie die Polarisation des Photons selbst. Ist eine elektromagnetische Welle genau parallel zum Polfilter orientiert, dann lässt er sie ungehindert durch, ist sie senkrecht polarisiert, dann kommt sie nicht durch:

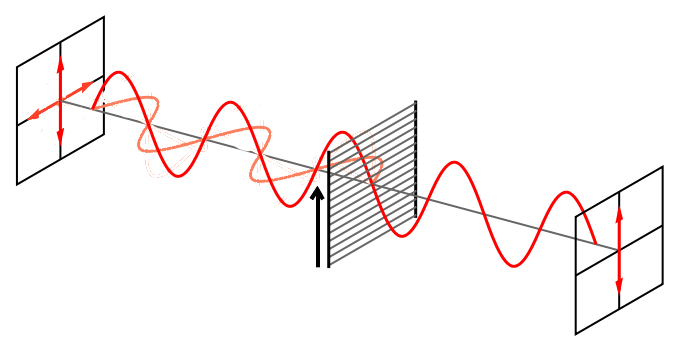
Bild von Bob Mellish . (modifiziert) Creative Commons Attribution-Share Alike 3.0 Unported license.

(Lasst euch nicht von den Linien auf dem Polfilter irritieren – die Richtung des Polfilters ist senkrecht zu den gezeichneten Linien, deshalb habe ich noch einen Pfeil in das Wikipedia-Bild eingebaut.)

Der Polfilter misst also den Zustand eines Photons: Ein Photon, das vertikal polarisiert ist, wird also niemals im Zustand “horizontal polarisiert” gemessen (es kommt niemals durch einen horizontal orientierten Polfilter) und umgekehrt. Ist die Polarisationsrichtung +45° (also nach rechts oben), dann kommt das Photon niemals durch einen Polfilter, der mit -45° orientiert ist und umgekehrt.

Und was passiert, wenn der Polfilter und die Polarisationsrichtung des Photons irgendwie zueinander verdreht sind? Zum Beispiel, wenn mein Photon in senkrechter Richtung polarisiert ist und ich es durch einen Filter schicke, der um +45° gedreht ist?

Wir können den Polarisationszustand des Photons in ein Diagramm eintragen:

Erinnert euch das an etwas? Die Situation ist genau analog zu der mit den Orts- und Energie-Zuständen aus dem letzten Teil. Vielleicht könnt ihr ja erraten, was passiert?

Den Zustand “senkrecht polarisiert” kann ich zusammensetzen aus “polarisiert unter +45°” und “polarisiert unter -45°”:

$|\uparrow\rangle = \frac{1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle$

Also hat das Photon eine Wahrscheinlichkeit von 50%, dass es durch den Filter unter +45° durchkommt (und dann also im Zustand +45° ist) und eine 50%-Wahrscheinlichkeit, dass es nicht durchkommt (dann wäre es im Zustand -45°, aber nicht wirklich, weil es vom Polfilter absorbiert wurde und deshalb nicht mehr existiert. Es ist dahingeschieden. Ein Ex-Photon…)

Waagerecht polarisiert geht entsprechend (beachtet das Minus-Zeichen):

$|\rightarrow\rangle = \frac{-1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle$

Sind Polfiltr und Polarisation des Photons um 45° gegeneinander verdreht, ist die Wahrscheinlichkeit, dass das Photon den Filter passiert, gerade 1/2, also das Quadrat der Amplitude. Das Nette an polarisierten Photonen ist also, dass man die unterschiedlichen Überlagerungen direkt geometrisch interpretieren kann und sofort sehen kann, wie die Zerlegung geht.

Als Übung könnt ihr ja mal versuchen, euch (vielleicht mit einer Zeichnung) zu überlegen, was passiert, wenn ich ein senkrecht polarisiertes Photon auf einen Polfilter schicke, der um einen anderen Winkel gedreht ist, zum Beispiel um 30°.

Wenn ihr es genau ausrechnet (und seinerzeit in der Schule bei der Trigonometrie gut aufgepasst habt), dann ist die Amplitude dafür, dass das Photon durch den Filter kommt, gleich dem Kosinus von 30°, die Amplitude für’s nicht-Durchkommen ist sin(30°). In Zahlen sind die Amplituden √3/2 und 1/2. Die Wahrscheinlichkeiten dazu könnt ihr durch Quadrieren bekommen, sie sind 3/4 und 1/4. Ist der Polfilter also nur wenig verdreht, ist die Wahrscheinlichkeit sehr hoch, dass das Photon durchkommt. Wenn man sehr viele Polfilter direkt übereinander stapelt und jeden ganz wenig gegen den davor verdreht, dann kann man die Polarisation des Lichts deswegen “mitdrehen”. Dieser Trick wird übrigens in jedem LCD-Bildschirm angewandt, weil die Flüssigkristalle wie kleine Polfilter wirken.

Dazu gibt es auch ein hübsches Bild bei Wikipedia:

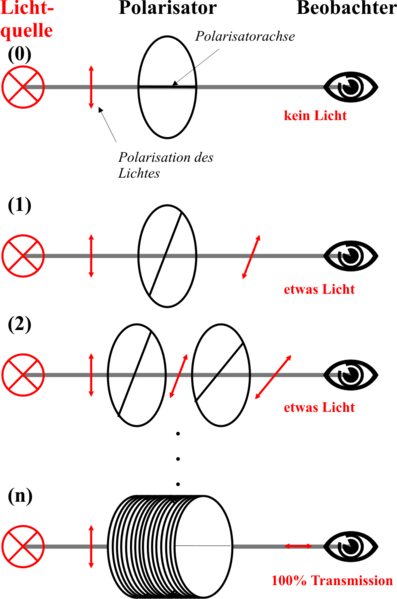
Von —Jkrieger 00:14, 17. Feb 2005 (CET) – selbst gezeichnet, Bild-frei, Link

Noch ein kleiner Tipp zum Lesen der Formeln (auch wenn sie euch jetzt im dritten Teil vermutlich nicht mehr schrecken): In vielen Formeln wie denen oben haben alle Summanden einen Vorfaktor $1/\sqrt{2}$ . Solche Vorfaktoren könnt ihr getrost erstmal ignorieren, sie sorgen am Ende dafür, dass die Summe aller Wahrscheinlichkeiten gleich 1 ist. Ich habe auch eine Weile überlegt, ob ich sie nicht einfach weglasse und statt der Gleichheitszeichen nur Proportionalzeichen verwende, das wäre aber unpraktisch für diejenigen, die tatsächlich mitrechnen wollen. Lasst euch davon also nicht abschrecken. (Tatsächlich gibt es aber sogar Physik-Paper, die genau das tun.)

Endlich: Verschränkung

Und jetzt habt ihr genug Wissen angehäuft, um zu verstehen, wie die berühmte quantenmechanische Verschränkung funktioniert. Warum es die Verschränkung gibt, kann ich euch auch nicht erklären – die Natur ist halt so merkwürdig. Aber wie man sie beschreibt, das könnt ihr jetzt hoffentlich relativ einfach verstehen.

Dazu brauchen wir zwei Photonen. Wir denken uns eine Quelle, die zwei Photonen aussenden kann, eins nach links und eins nach rechts. Dort messen wir (bzw. die beiden PhysikerInnen Alice und Bob, deren Job das traditionell ist) die Polarisation der Photonen.

Jedes von ihnen (also von den Photonen, nicht von Alice und Bob) kann in einem Zustand sein – ich schreibe einfach die beiden Zustände nebeneinander (im ersten Teil habe ich gesagt, dass man Zustände nicht multiplizieren darf, aber hier geht das, weil die Zustände zu unterschiedlichen Photonen gehören). Ein einfacher Zustand für die beiden Photonen wäre
$|\uparrow\rangle |\uparrow\rangle$
In diesem Zustand sind beide Photonen senkrecht polarisiert – verschränkt ist da noch nichts.

Wir können auch die beiden Photonen jeweils in einem Überlagerungszustand haben. Nehmen wir an, beide sind unter -45° polarisiert, das würde dann so aussehen:
$|\nearrow\rangle|\nearrow\rangle= \left(\frac{1}{\sqrt{2}} |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle \right) \left(\frac{1}{\sqrt{2}} |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle \right)$

Die linke Klammer beschreibt das eine Photon, die rechte das andere. Ihr könnt diesen Zustand umschreiben, wenn ihr die Klammern ausmultipliziert – dabei gelten die ganz üblichen Rechenregeln. Wenn ihr (und ich) alles richtig macht, dann ist das Ergebnis:

Jede der vier Möglichkeiten für die beiden Polarisationen hat eine Wahrscheinlichkeit von 1/4.

Was passiert, wenn ihr beispielsweise das linke Photon (das, das nach links zu Alice fliegt und zu dem der linke Zustand gehören soll) durch einen Polfilter schickt und messt? Nehmt an, der Polfilter ist senkrecht orientiert und das Photon kommt durch den Filter durch. Wie sieht dann der Zustand hinterher aus? (Wendet einfach ohne langes Nachdenken die Regeln aus dem ersten Teil an).
Im ersten Teil haben wir gelernt, dass man alle Terme wegstreicht, die nicht zur Messung passen, und dann den Vorfaktor so anpasst, das alle Wahrscheinlichkeiten stimmen. Wegstreichen müssen wir also die Terme, bei denen das erste Photon im Zustand $|\rightarrow\rangle$ ist. Der verbleibende Zustand ist

$\frac{1}{\sqrt{2}} |\uparrow\rangle |\uparrow\rangle + \frac{1}{\sqrt{2}} |\uparrow\rangle |\rightarrow\rangle$

Und das können wir wieder umschreiben als

$|\uparrow\rangle \left( \frac{1}{\sqrt{2}} |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle \right) = |\uparrow\rangle |\nearrow\rangle$

Was sagt uns das? Der Zustand des rechten Photons wird von dem des linken überhaupt nicht beeinflusst. Nix mit quantenmystischer Verschränkung. Aber keine Sorge, wir können unsere Photonen problemlos verschränken. (Wie man’s technisch macht, erkläre ich hier nicht, vielleicht ein andermal). Dazu bauen wir diesen Zustand hier:

$\frac{1}{\sqrt{2}} |\uparrow\rangle |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle |\rightarrow\rangle$ .

Stellt euch dasselbe Experiment wie eben vor – wieder passiert das linke Photon den senkrechten Polfilter. Was heißt das für den Zustand?

Der Zustand ergibt sich wie sonst auch, indem man die Terme wegstreicht, die nicht zur Messung passen. Das ist hier der zweite Term. Was übrig bleibt ist also nur $|\uparrow\rangle|\uparrow\rangle$ .

Das rechte Photon, für sich allein betrachtet, war vorher im Zustand $\frac{1}{\sqrt{2}} |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle$ , aber nach der Messung des linken Photons hat sich der Zustand des rechten Photons geändert.

Und das (Ta-daa!) ist jetzt die quantenmechanische Verschränkung.

Wir weisen die Verschränkung nach

“Halt, Stopp,” mag jetzt der eine oder die andere rufen, “sooo einfach ist es doch nun wirklich nicht. Ich messe, dass die beiden Photonen immer dieselbe Polarisation haben, o.k. Und weil das ganze ein statistisches Geschäft ist, messe ich in 50% der Fälle die senkrechte und in 50% der Fälle die waagerechte Polarisation. Dafür brauche ich keine Quantenmechanik. Wer sagt denn, dass die Photonen nicht einfach in 50% der Fälle gleich mit der einen Polarisation losfliegen und in 50% der Fälle mit der anderen? Das kann ich mit diesem Experiment überhaupt nicht nachweisen.”

Richtig. Stimmt genau. Um die Verschränkung wirklich nachzuweisen (und nicht einfach nur zu glauben), müssen wir beweisen, dass die Photonen nicht schon beim Losfliegen eine eindeutige Polarisation haben. Momentan können wir das Experiment noch so interpretieren:
Beim Aussenden der Photonen entscheidet sich, ob die beiden Photonen im Zustand $|\uparrow\rangle|\uparrow\rangle$ oder im Zustand $|\rightarrow\rangle|\rightarrow\rangle$ . Jeden dieser Zustände haben sie mit einer Wahrscheinlichkeit von 50%.

Um nachzuweisen, dass das nicht sein kann, müssen wir die Polfilter drehen. Nehmen wir an, unsere einfache – sozusagen “klassische” – Erklärung wäre richtig. Was würde passieren, wenn wir an den beiden Messpunkten am Ende die Polfilter drehen, wie üblich um 45°?

(Denkpause…)

Wenn das Photon, das nach links fliegt, senkrecht polarisiert ist, hat es eine 50%-Wahrscheinlichkeit, den Polfilter zu passieren. Ebenso auch, wenn es waagerecht polarisiert ist. Dasselbe gilt für das zweite Photon. Die Ergebnisse der beiden Photonen sind aber vollkommen unabhängig voneinander – wir würden also erwarten, dass wir vier mögliche Ergebnisse bekommen: $\nwarrow \nwarrow,\ \nwarrow \nearrow,\ \nearrow \nwarrow,\ \nearrow \nearrow$ . (Ich habe das jetzt, weil es Messergebnisse sind, nicht als Zustände geschrieben, ich hoffe, das ist nicht verwirrend.) Jedes dieser Ergebnisse sollte die gleiche Wahrscheinlichkeit haben, also 1/4 oder 25%. Das ist die Vorhersage der klassischen Physik.

Und was sagt die Quantenmechanik? Nach all der Rechnerei könnt ihr das – mit etwas Mühe – selbst rausfinden. (Wenn euch das zu viel Mühe ist, dürft ihr mir das Endergebnis aber auch glauben – ich hofe, ich habe mich nicht verrechnet.) Nehmt den quantenmechanischen verschränkten Zustand, den ich oben hingeschrieben habe:

$\frac{1}{\sqrt{2}} |\uparrow\rangle |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle |\rightarrow\rangle$

Und jetzt zerlegt ihr den Zustand jedes Photons entsprechend den Rechenregeln für die Polarisation, die wir oben hingeschrieben haben:

$|\uparrow\rangle = \frac{1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle$

$|\rightarrow\rangle = \frac{-1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle$

Setzt das jeweils für jeden der Zustände oben ein (dabei muss man ein bisschen aufpassen, welcher Zustand zu welchem Photon gehört). Jeder der beiden Summanden ergibt vier Terme. Im ersten Summanden sind alle vier Terme positiv, im zweiten sind zwei der vier negativ:

$\frac{1}{\sqrt{2}} \left( \frac{1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle\right) \cdot \left( \frac{1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle\right) +$
$\frac{1}{\sqrt{2}} \left( \frac{-1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle\right) \cdot \left( \frac{-1}{\sqrt{2}} |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle\right)$

Puh. Wenn ihr das jetzt ausmultipliziert, dann seht ihr, dass sich die gemischten Terme genau wegheben. Übrig bleibt
$\frac{1}{\sqrt{2}} |\nwarrow\rangle |\nwarrow\rangle + \frac{1}{\sqrt{2}} |\nearrow\rangle |\nearrow\rangle$

Was passiert, wenn ich jetzt das erste Photon messe und es den Polfilter passiert? Den unpassenden Term des Zustands streiche ich weg – es bleibt also übrig, dass auch das zweite Photon im selben Polarisationszustand ist wie das erste. Es ist also egal, ob ich die Polfilter senkrecht/waagerecht oder unter -45°/+45° aufstelle – die beiden Photonen sind immer gleich polarisiert.

Und genau das lässt sich mit dem klassischen Modell nicht erreichen.

Hier noch mal das Argument in Kurzform (im wesentlichen geklaut bei mir selbst):

1. Passiert das eine Photon den senkrechten Polfilter, dann auch das andere. Beide Photonen sind also gleich polarisiert.
2. Wenn wir annehmen, dass der Zustand des Photons eindeutig ist und das eine Photon das andere nicht beeinflussen kann, dann müssen die Photonen also in einem eindeutigen Zustand losfliegen – entweder beide senkrecht oder beide waagerecht polarisiert..
3. Trifft ein senkrecht polarisiertes Photon auf einen Polfilter unter 45°, dann wird es mit 50% Wahrscheinlichkeit durchgelassen, mit 50% Wahrscheinlichkeit absorbiert. Welcher Fall eintritt, ist zufällig.
4. Passiert das eine Photon den Polfilter unter 45°, dann auch das andere.

5. Genau wie bei 2. können wir folgern, dass die Photonen entweder unter +45° oder unter -45° polarisiert erzeugt werden.

Und dabei ist 5. ein Widerspruch zu 2, denn ein Photon kann nur einen eindeutigen Polarisationszustand haben.

Um die Verschränkung nachzuweisen, müssen wir also die Polfilter an den beiden Messstellen jeweils in vier unterschiedlichen Polarisationsstellungen einstellen. Alice und Bob können einen vierseitigen Würfel (1W4 für Rollenspieler) werfen und entscheiden, welche Stellung der Polfilter haben soll. Um ganz sicher zu gehen, dass die Stellung der Polfilter die Polarisation nicht beeinflussen kann, können die beiden das auch erst entscheiden, kurz bevor die Photonen bei ihnen eintreffen, so dass kein Signal (mit Lichtgeschwindigkeit) den anderen Polfilter erreichen kann. (Ja, das hat man experimentell tatsächlich so gemacht.)

Nach dem Experiment vergleichen Alice und Bob ihre Ergebnisse. Nehmen wir an, so sahen sie aus:

Alice		Bob
Filter	Messung	Filter	Messung
+45	0	-45	1
-45	0	-45	0
0	1	90	0
90	0	0	1
+45	0	0	0
+45	0	-45	1
90	1	+45	1
0	1	90	0
0	0	+45	1
90	0	0	1
-45	0	90	0
90	1	90	1

Dabei steht eine 1 für “Photon kommt durch den Filter” und die 0 für das Gegenteil. Dann ignorieren sie alle Fälle, bei denen die Polfilter nicht entweder parallel oder um 90° zueinander verdreht waren. (Wenn also Alice unter +45° gemessen hat und Bob senkrechte Polarisation, dann nützt uns das hier nicht viel.) Bei den übrigen Experimenten vergleichen sie:

Alice		Bob
Filter	Messung	Filter	Messung
+45	0	-45	1
-45	0	-45	0
0	1	90	0
90	0	0	1
+45	0	-45	1
0	1	90	0
90	0	0	1
90	1	90	1

Sie stellen fest, dass ihre Photonen immer im selben Zustand angekommen sind, egal wie die Winkelstellung war. Hatten sie beide dieselbe Stellung, dann haben beide eine 1 oder 0 gemessen, hatten sie um 90° verdrehte Stellungen, dann bekommt der ene die 1, der andere die 0. Das ist die Verschränkung, genau wie oben beschrieben.

Ihr könnt an diesem Experiment auch gleich ein sehr wichtiges Ergebnis sehen: Um die Verschränkung tatsächlich nachzuweisen, müssen die beiden ihre Ergebnisse auf herkömmlichen Wege austauschen. Alice kann allein aus ihren Daten nicht sehen, was Bob gemacht hat (nicht einmal, ob Bob nicht lieber einen Kaffee trinken gegangen ist, weil er Quantenmechanik langweilig findet). Obwohl also die Messungen sich gegenseitig beeinflussen, so dass immer derselbe Polarisationszustand herauskommt, kann man mit Hilfe der Verschränkung keine Nachrichten verschicken.

Ich gebe zu, dass das Argument ein bisschen kompliziert ist. Man muss ein paar Mal drüber nachdenken (ich erinnere mich, dass ich über den entsprechenden Abschnitt in den Feynman Lectures lange gebrütet habe) – also nicht verzweifeln, wenn ihr nicht auf Anhieb seht, wie’s geht. Falls ihr gar nicht klarkommt, dürft ihr natürlich gern in den Kommentaren nörgerln oder nachfragen.

Tja, auf diesen dritten Teil, in dem ich endlich die Verschränkung erkläre, musstet ihr ganz schön lange warten. Nicht nur, weil ich doch etwas grübeln musste, wie es am besten geht, auch nicht nur, weil ich zwischendurch auf Dienstreise war, einen Workshop und eine Doktorprüfung (als Prüfer) hatte, sondern vor allem, weil ich in den letzten zwei Wochen mehr Zeit beim Augenarzt als sonstwo verbracht habe – immerhin ist meine Netzhaut jetzt in beiden Augen dank Argonlaser sicher festgetackert (auch wenn das linke Auge immer noch – bisher nicht klar diagnostizierte – Sehstörungen hat).

Kommentare (122)

#1 rolak
27. Januar 2013

Schöner post – schlägt das ehedemige Ritual des Zeitunglesens am Sonntag (mit viel und einer Zeit) deutlich. Nachträglich und weiterhin gute Besserung übrigens.

festgetackert

boah, das benötigt aber eine eigene Triggerwarnung – schon bei der kleinsten Vorstellung Auge+Krampen krampft sich alles zusammen^^

Wie immer nicht themenbezogen, jedoch sehr weiterlesefreundlich: Die kleinen Gags am Rande. “Das Photon und sein Ex – Double Bind war gestern, Verschränkung ist schrecklicher”, Klassiker der Weltliteratur, zwischen Freud und Courths-Mahler.
#2 MartinB
27. Januar 2013

@rolak
Naja, das wird nicht echt getackert sondern mit nem Laserstrahl gezielt verbrannt – tut weh, ist aber besser als die Alternative (am Augapfel vorbei von hinten mit nem Kryo-Gerät anfrieren…).
#3 rolak
27. Januar 2013

nicht echt

Klar, MartinB, deswegen auch mein Nichtvorschlag mit der TW. Eine durchaus gängige und zutreffende Formulierung, hätte auch von mir sein können – nur lösen bei mir (nicht nur) solche Formulierungen Bilderkaskaden aus, die dann wiederum eher unangenehm sind.
Selbst das komplett richtige ‘Punktschweißen’ hätte eher solche Bilder generiert, gruselig…

Kann auch beim Auge besonders intensiv ausgeprägt sein, weil mir zu Teeniezeiten mal einer mit seinem Minigolfschläger ausholend (unabsichtlich) rechts das Brillenglas zerklopft und einen guten Satz Splitter in und um dem Auge hinterlassen hat. Will aber nicht meckern, das gab ein Jahr freien Eintritt 😉 Trotzdem, da zu liegen und dauernd den Arzt aufs Auge zukommen zu sehen ist nicht so lustig gewesen.
#4 tomek
28. Januar 2013

Mal wieder ein guter Artikel.
Auch wenn man als Physikstudent das schon einmal gehört hat, so schön bekommt man es in keiner Vorlesung erklärt 😉
#5 roel
*****
28. Januar 2013

@MartinB Erstmal wieder viel Lob für diese tolle Serie. Hoffentlich bleiben die Pfeile erhalten, aber ich habe es mir vorsichtshalber abgespeichert. Und dann natürlich gute Besserung und viel Erfolg für die weitere Behandlung.
#6 Bernd
28. Januar 2013

Passend zu diesem Artikel liefert Google-Anzeigen einen Link zur “Quantenheilung”. Das läuft aber vermutlich nicht unter “verschränkt”, sondern eher unter “beschränkt”.

😉
#7 MartinB
28. Januar 2013

@Bernd
Tja, da läuft halt irgendein Suchalgorithmus mit Schlüsselwörtern.
#8 SCHWAR_A
29. Januar 2013

Hallo Martin,
einen komplizierten Zusammenhang schön dargestellt!

Kommt es mir nur so vor, oder sind hier immer beide Photonen identisch ausgerichtet? Dann nämlich hätte bei _echt_zufälliger_ Ausrichtung des einen Photons das andere die Wahrscheinlichkeit p=1, weil es ja durch Verschränkung _sicher_ genauso ausgerichtet ist.

Ich habe mal irgendwo gelesen, daß bei der Erzeugung verschränkter Objekte beide immer zueinander komplementär seien – also zB. das eine Photon ↑ und das andere damit →. Ist das so?

Herzliche Grüße.
#9 MartinB
29. Januar 2013

@SCHWAR_A
Ich habe den Zustand so gebaut, dass die verschränkten Photonen immer gleich polarisiert sind. Das gegenteil ist auch möglich. Ich sehe auch keinen Grund, warum das bei Photonen anders sein sollte – bei Elektronenspins sollten bei einer Verschränkung die Spins wohl entgegengesetzt sein, sonst gibt es Ärger mit dem Pauli-Prinzip.
#10 Pumba
29. Januar 2013

Was ich mich immer frage ist wieso denn nun diese beiden photonen miteinander verschränkt sind. Könnten sie nicht mit irgendwelchen anderen auch verschränkt sein? Bzw woher weiß man welche photonen mit welchen verschränkt sind?

Übrigens eine tolle serie 🙂 fand ich sehr cool!
#11 MartinB
29. Januar 2013

@Pumba
Normalerweise geht die Verschränkung schnell verloren – das sieht man ja auch am Beispiel hier. Nach der Messung der beiden Polarisationen ist die Verschränkung weg, jedes Photon ist in einem bestimmten Zustand.
Zum Problem, was denn genau eine Messung ist, habe ich hier mehr geschrieben, vielleicht hilft das:
https://scienceblogs.de/hier-wohnen-drachen/2012/10/10/quantenmechanik-und-realitat/
#12 Dr. Webbaer
30. Januar 2013

Es ist also egal, ob ich die Polfilter senkrecht/waagerecht oder unter -45°/+45° aufstelle – die beiden Photonen sind immer gleich polarisiert.

Helfen Sie bitte einmal ein wenig dem Schreiber dieser Zeilen: Ein geeignet gesplittetes Photon wird abgefragt über geeignete Polarisierungsfilter und die Filterergebnisse, also das Durchlassen betreffend, sind bei den Gesplitteten jeweils gleich, also sie gehen beide durch oder beide nicht.

Und daraus wird gefolgert, dass die beiden Teile eigentlich eher einem Teil entsprechen, WEIL sie nicht so viele (nämlich: unendlich viele) Eigenschaftswerte tragen können wie später abgefragt, korrekt?

MFG
Dr. W
#13 Patrick
30. Januar 2013

@Martin
Ich wünsche Dir gute Besserung für deine Augen und dass alles wieder in Ordnung kommt.
Danke für die tollen Erklärungen. Etwas verstehe ich noch nicht. Unter einer Multiplikation eines Bra und eines Kets stelle ich mir ein Skalarprodukt vor. Aber was ist mit der Multiplikation zweier Kets gemeint?
#14 MartinB
30. Januar 2013

@Patrick
Die Multiplikation zweier kets ist einfach der Zustand der beiden Photonen (das eine Ket gehört zum einen, das andere zum anderen), ich hätte auch die beiden Pfeile in ein ket reinschreiben können. Beides ist in der Physik als Notation gebräuchlich.
#15 Patrick
30. Januar 2013

@Martin
Danke, ich glaube, ich verstehe es. Dann müsste das wohl ein Ket mit 4 Dimensionen sein.
#16 Volker Distelrath
Waakirchen
30. Januar 2013

Martin, ich wünsche Dir den medizinisch optimalen Durchblick, auch auf dem linken Auge, und mir, auch nach mindestens dreimaligem Lesen Deines wieder hervorragenden Beitrags den Hauch eines mentalen Durchblicks, was Verschränkung “wirklich” ist. Mathematisch soweit klar, aber warum, zum Schrödinger nochmal, tun das diese Biesterchen?
#17 MartinB
30. Januar 2013

@Volker
Warum? So ist die Welt halt – wer weiß, wie langweilig ein klassisches Universum wäre…
#18 Erik der Unlesbare
31. Januar 2013

Jetzt wird schon ein zweites mal nach dem Sinn von Q-Verschränkung gefragt. Sicher war die erste Antwort keine ausreichende Antwort. Die zweite Antwort ist eher ein Ausweichen. Ein Physiker, der in seiner Jugend die Kräfte von Elementarteilchen simulieren wollte, kann sicher mehr in seine Antwort packen.
Ich habe eine Antwort auf den Sinn von Q-Verschränkung im Universum. Leider beziehe ich mein Wissen aus “freier Assoziation”, welche von MB (Master-Brain vom Blog) nicht gefördert wird.

– Die jetzt ein wenig von mir zugespitzte Darstellung gehört zum Verstehen, welche Bewegungen in einem von “Quanten-Zeit” geführten Raum möglich sind. Die Entscheidung vom Master-Brain (im Sinne eines Boltzmann-Brains) wird den Fortgang bestimmen. Ich bin schon enorm gespannt (kann man in eV messen).
#19 Dr. Webbaer
31. Januar 2013

Noch einmal nachgefragt hierzu:
‘Dazu brauchen wir zwei Photonen. Wir denken uns eine Quelle, die zwei Photonen aussenden kann, eins nach links und eins nach rechts. Dort messen wir (bzw. die beiden PhysikerInnen Alice und Bob, deren Job das traditionell ist) die Polarisation der Photonen.’

Wir splitten sozusagen ein Photon und haben dann zwei Photonen, die in unterschiedliche Richtungen unterwegs sind. Wir prüfen dann jeweils die Polarisation mit einem geeigneten Filter, der unter bestimmten Umständen den Durchlass mit einer 50%-Wahrscheinlichkeit erlaubt. Wir stellen überrascht fest, dass beide Photonen jeweils durchgelassen werden oder nicht.

Zu erwarten wäre der statistische mit 50%-Wahrscheinlichkeit Durchlass, aber kein Gleichverhalten.

Korrekt?
Und “verborgene Variablen” schließt man wie genau aus?

MFG
Dr. W
#20 MartinB
31. Januar 2013

@Webbär
Etwas unscharf ausgedrückt, aber soweit ich sehen kann korrekt.

Das Ausschließen “Verborgener Variablen” ist etwas knifflig – das Bellsche Theorem zeigt, dass es keine lokalen verbborgenen Variablen geben kann (es gibt keine Möglichkeit, den Zustand der Photonen einfach beim losfliegen festzulegen, egal wie viele Variablen man hat); nichtlokale verborgene Variablen sind aber denkbar:
https://en.wikipedia.org/wiki/Hidden_variable_theory
#21 rolak
31. Januar 2013

Wir splitten sozusagen ein Photon

Nein, es sind von Anfang an zwei. Mit einem sich aus dem Prozeß der Verschränkung ergebenden Gesamtzusammenhang, hier: ‘Gleiche Polarisierung’.

“verborgene Variablen” schließt man wie genau aus?

Durch experimentelles Überprüfen der Bellschen Ungleichung.
#22 rolak
31. Januar 2013

.. und so was ist eine aus unabhängig wahrgenommener er Lokalzeit sich ergebende Kommentarverschränkung…

Schon wieder die nichtlokalen verborgenen V vergessen^^
#23 MartinB
31. Januar 2013

@rolak
Nein, der Wb hat – zumindest manchmal – recht: Eine momentan häufig genutzte Technik zum Herstellen von verschränkung ist diese hier:
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
#24 rolak
31. Januar 2013

Ahso MartinB, das ist eine etwas andere Auslegung von ‘split’ als die, die mir vor Augen lag. Mit dieser laxen Bedeutungsaufweitung kann selbstverständlich auch ein Elementarteilchen geteilt werden.
Schon um den in den letzten Worten lauernden Widerspruch zu vermeiden würde ich den Prozeß anders umschreiben: Durch die Absorption eines Photons p wird das System chi-square dazu angeregt, zwei verschränkte Photonen p/2 zu emittieren. Klingt mir einfach schmerzfreier, doch das ist selbstverständlich lokal…
#25 Dr. Webbaer
31. Januar 2013

Ja, danke. Vielleicht erklären Sie dem Schreiber dieser Zeilen wie auch der Menge beizeiten den Unterschied zwischen einer lokalen und nichtlokalen Eigenschaftvariablen.

MFG
Dr. W (den mehr die informatorisch-philosophische Dimension interessiert und physikalischer Theoretisierung nur schwierig folgen kann)
#26 MartinB
31. Januar 2013

@rolak
Ja, dem stimme ich zu, ich wollte aber den Webbärschen Kommentar nicht über die Maßen kritisieren…

@Wb
Nichtlokal bedeutet einfach, dass die Messung des einen Photons die verborgenen Variablen des anderen irgendwie beeinflussen kann.
#27 rolak
31. Januar 2013

dem stimme ich zu

Oh schön.
Allerdings war meine ‘split’-Kritik trotzdem unberechtigt, da offensichtlich der Prozeß (auch) so bezeichnet wird.
#28 Dr. Webbaer
2. Februar 2013

Nichtlokal bedeutet einfach, dass die Messung des einen Photons die verborgenen Variablen des anderen irgendwie beeinflussen kann.

Wobei aber nie bewiesen werden kann, dass nicht beide (gesplittete) Probanden Eigenschaftenwerte tragen, die sie gegenüber jedweder Prüfabfrage oder zumindest die gemeinten betreffend mit ihren Polarisationsfiltern erlauben synchron zu antworten.

Würde der Schreiber dieser Zeilen zumindest annehmen wollen, systematisch-philosophischen Überlegungen folgend.

Wenn beide Probanden geeignet sind jedwede Abfrage identisch zu beantworten, hätte man den Salat mit dem “nichtlokal”.

MFG
Dr. W (der ansonsten keine grundsätzlichen Probleme hat mit dem Gedanken, dass die Lokalität wie die Zeitlichkeit menschlicher Abstraktion unterliegt und zwar nur dieser)
#29 MartinB
2. Februar 2013

@Webbär
Nein, es ist nachweisbar unmöglich, dass keine Nichtlokalität in den verborgenen Variablen steckt, egal was “systematisch-philosophische” Überlegungen sagen. (Stichwort dazu “Bellsche Ungleichung” – der Wikipedia-Artikel dazu sollte nach Lektüre dieser Serie eigentlich zu verstehen sein, ansonsten hatte Jörg Friedrich seinerzeit eine kleine Serie dazu, in der das auch erklärt wrde (die lässt sich sicher noch irgendwie auftreiben, Stichwort EPR).)
#30 Dr. Webbaer
3. Februar 2013

Herr Bäker, die Texte und Theorien sind ja zK genommen worden, systematisch-philosophische Überlegungen lassen die Es-Gibt-Aussage bezogen auf “versteckte Variablen” aber als nicht falsifizierbar erscheinen. Korrekt ist wohl, dass sich die Bellsche Ungleichung als Theorie bewährt hat. – BTW: Kann man sich der scheinbaren Paradoxie der Verschränkung mit einem Gleichnis annähern. das ohne spezielle physikalische Kenntnisse auskommt?

MFG + danke für Ihre kommentarischen Bemühungen,
Dr. W
#31 MartinB
3. Februar 2013

“systematisch-philosophische Überlegungen lassen die Es-Gibt-Aussage bezogen auf “versteckte Variablen” aber als nicht falsifizierbar erscheinen.”
Dann sind diese systematisch-philosophischen Überlegungen leider falsch (oder ich verstehe – wie so oft – die Webbärsche Semantik nicht).

“Kann man sich der scheinbaren Paradoxie der Verschränkung mit einem Gleichnis annähern. das ohne spezielle physikalische Kenntnisse auskommt?”
Weiß ich nicht. Ich habe hier im Blog ja schon öfterns drüber geschrieben – die Erfahrung zeigt, dass zu bildhate Gleichnisse dem Verständnis nicht förderlich sind.
Wenn man Verschränkung verstehen will, muss man sich wohl oder übel einmal hinsetzen und das, was ich hier in den drei teilen erklärt habe, verstehen – das ist wie mit Euklid, den Königsweg gibt’s nicht.
#32 MisterA
7. Februar 2013

Hallo MartinB, schöne Serie wie immer 🙂
Ich hab mal eine Frage die jetzt weniger mit dem Thema zu tun hat(im tieferen Sinne eigentlich schon). Aber kommt die ganze Physik eigentlich ohne einen Kraftbegriff aus? Da man ja Sachen wie den Lagranian, Hamiltonian, Erhaltungsgrößen(die ja auch aus der QM folgen) usw. hat. die man benutzen kann. ?

Gruß
#33 MisterA
7. Februar 2013

Und die Gravitationskraft ja nach der ART durch eine Geometrie beschrieben wird.
#34 MartinB
8. Februar 2013

@MisterA
Naja, man kommt schon irgendwie ohne aus, denke ich, aber manchmal ist er halt sehr nützlich. Physik ist ja immer in vieler Hinsicht voller redundanzen (es gibt oft mehrere Darstellungen desselben Sachverhalts), siehe auch hier:
https://scienceblogs.de/hier-wohnen-drachen/2011/07/24/buchersommer-r-feynman-the-character-of-physical-law/
#35 Wolfgang Birkholz
Berlin
1. März 2013

Super-Darstellung! Aber eine Basis-Frage: 2 in der Polarisation verschränkte Photonen fliegen in unterschiedlicher Richtung davon (z.B. erzeugt mit 2 nichtlinearen Kristallen). Ich absorbiere das eine Photon. Was passiert mit dem anderen? Ist es auch weg oder gehen alle bis dahin über beide verteilten Eigenschaften auf dieses andere Photon über?

Dank und lg, Wolfgang
#36 MartinB
2. März 2013

@Wolfgang
Weg ist das andere Photon nicht. Was mit seiner verschränkten Eigenschaft passiert (z.B. der Polarisation) hängt davon ab, ob du die beim Absorbieren des ersten Photons gemessen hast. Wenn ja, dann gelangt das zweite Photon in den passenden Zustand, wenn nein, dann bleibt es im Überlagerungszustand, der dann aber mit nichts mehr verschränkt ist.
#37 Wolfgang Birkholz
Berlin
2. März 2013

Vielsten Dank für die schnelle Antwort! Und es ist doch sicher so, dass man keine Chance hat, durch eine Messung am übriggebliebenen Photon festzustellen, ob dieses nun vor der Messung durch die platte Absorbierung des ursprünglichen Partners schon in den “passenden” Zustand gezwungen wurde, oder ob das Messergebnis am übriggebliebenen Photon aufgrund der Auflösung des Überlagerungszustandes infolge der Messung zustande gekommen ist. Und damit ist die simple Vorstellung vom Morsen geplatzt, um eine Informationsübertragung schneller als die Lichtgeschwindigkeit (c) hinzubekommen.
Abseits von diesem realen Teil der Physik: Warum sollte eine Informationsübertragung schneller als c nicht möglich sein? Signalübertragung >c ist ja möglich. Und eine Informationsübertragung >c steht nach meiner Auffassung nicht im unüberwindbaren Widerspruch zu Einstein, wo es immer um Masse bzw. Energie geht. Aber “reine” Information muss doch daran nicht zwingend gebunden sein. Und deshalb Informationsübertragung zwingend auch nicht. Meine Hoffnung war/ist, dass Verschränkung ein erfolgreicher Weg sein könnte, Information masse- bzw. energielos übertragen zu können oder anders ausgedrückt, Signal- und Informationsübertrgung strenger zu verheiraten. Man müsste als erstes “nur” physikalisch exakt definieren (können), was Information ist. Sorry, das ist Philosophie, die in früheren Zeiten fruchtbar mit der Physik zusammengearbeitet hat.
#38 MartinB
2. März 2013

” Und es ist doch sicher so, dass man keine Chance hat…”
Richtig.

“Signalübertragung >c ist ja möglich”
Nur wenn man den Begriff “Signal” sehr ungewöhnlich definiert. Da kommen wir jetzt in den Bereich der Interpretation der QM – nicht alle Interpretationen sind nicht-lokal.

“Aber “reine” Information muss doch daran nicht zwingend gebunden sein.”
Mir ist kein Fall von materie- und energieloser Information bekannt.

“Meine Hoffnung war/ist, dass Verschränkung ein erfolgreicher Weg sein könnte, Information masse- bzw. energielos übertragen zu können ”
Das ist mit der QM gegenwärtig nicht vereinbar, da geht das defintiv nicht.

“Man müsste als erstes “nur” physikalisch exakt definieren (können), was Information ist. ”
Da gibt es bereits diverse Definitionen – keine davon erlaubt aber eine überlichtschnelle Informationsübertragung.
#39 Dr. Webbaer
2. März 2013

Man müsste als erstes “nur” physikalisch exakt definieren (können), was Information ist..

Es scheint möglich so die “intergalaktischen Lottozahlen” vom Zentrum der Galaxis aus möglichst günstig zu verbreiten bzw. auszulosen. Oder auch einen Code für die nachfolgende Verschlüsselung von Kommunikation zu verteilen. – Wobei dann bei den Empfängerstationen der verschränkten Datenübertragung der Eindruck entstehen müsste, dass die Information überlichtschnell verbreitet worden ist.

Information ist das, was ein Erkenntnissubjekt aus einer erhaltenen Datenmenge (Code) macht bzw. abstrahiert, wobei für die Zwecke der Kommunikation in der Regel diese Datenmenge mit Hilfe eines Algorithmus kodiert worden ist. Abstrahieren von Daten, Kodieren zu Daten, so die Gegensätzlichkeit.

MFG
Dr. W
#40 MartinB
2. März 2013

@Wb
Wenn das immer noch möglich scheint, dann haben Sie es wirklich absolut gar nicht verstanden.
#41 Dr. Webbaer
2. März 2013

@Bäker
Schreiben Sie doch wenigstens WAS I.E. nicht verstanden worden ist. Sie werden feststellen, dass, wenn Sie dies tun, doch etwas verstanden worden ist.

Ist denn von Ihnen verstanden worden, dass durch (multiple) Verschränkung Dienste wie oben beschrieben funktionieren können, die bspw. Schlüssel (offensichtlich Objekte der Abstraktion zu Information betreffend) übertragen, die sich erst vor Ort manifestieren und nutzbar werden?!
War das mit der “intergalaktischen Lotterie” so wenig nachvollziehbar?

MFG
Dr. W
#42 MartinB
3. März 2013

“War das mit der “intergalaktischen Lotterie” so wenig nachvollziehbar?”
Ja, denn wie oben im Artikel erläutert, kann die verschränkt übertragene “Information” erst dann ausgelesen werden, wenn die Messergebnisse von Alice bei Bob ankommen.
#43 Dr. Webbaer
3. März 2013

@Bäker

War das mit der “intergalaktischen Lotterie” so wenig nachvollziehbar? (Dr. W)

Ja, denn wie oben im Artikel erläutert, kann die verschränkt übertragene “Information” erst dann ausgelesen werden, wenn die Messergebnisse von Alice bei Bob ankommen.

Moment, Alice oder Bob wird die Messung zuerst vornehmen, wobei dann die zuerst vorgenommene Messung das Resultat auf der jeweils anderen Seite bestimmt, gleiche Messeinstellungen vorausgesetzt.

Das entspricht – https://scienceblogs.de/hier-wohnen-drachen/2013/01/27/quantenmechanik-verstehen-iii-verschrankung/#comment-13612 – einem mehrfach versendeten Würfel dessen Wurf zwar nicht vorhersehbar ist, dessen einmal festgestelltes Ergebnis (bei Alice oder Bob) aber das Wurfergebnis späterer und an anderer Stelle vorgenommenen Würfe bestimmt.

Falls korrekt angenommen, wäre so über n-fache Verschränkung ein spezieller Lotteriedienst realisierbar.
Oder eben der oben beschriebene Dienst zum Versand zufälliger, aber eindeutiger Schlüssel, die von und zwischen den einzelnen Stationen dann bspw. für kryptographische Zwecke genutzt werden könnten.

Sollte das korrekt festgestellt sein, könnte in der Folge noch einmal über die Information philosophiert werden, die ein derartiger Dienst nichtlokal trägt.

MFG
Dr. W (der Ihnen für Ihre Antworten dankt)
#44 MartinB
3. März 2013

“wobei dann die zuerst vorgenommene Messung das Resultat auf der jeweils anderen Seite bestimmt, ”
Nein. Wegen der Relativität ist es nicht unbedingt möglich zu sagen, wer zuerst gemessen hat, das hängt vom bezugssystem ab:
https://scienceblogs.de/hier-wohnen-drachen/2012/10/10/quantenmechanik-und-realitat/

“essen einmal festgestelltes Ergebnis (bei Alice oder Bob) aber das Wurfergebnis späterer und an anderer Stelle vorgenommenen Würfe bestimmt.”
Sie können das so oft in unterschiedlichen Varianten schreiben, wie Sie wollen, es wird dadurch nicht richtiger. Bob misst sein Photon beispeilsweise im Zustand senkrecht polarisiert. Welche Botschaft hat Alice ihm geschickt?

Um irgend etwas über die Verschränkung mit Alice’s Photon zu erfahren, muss er das Ergebnis ihrer Messung mitgeteilt bekommen, aus der Information “senkrecht polarisiert” allein kann er nichts darüber wissen, ob Alice’s Photon mit seinem verschränkt war, was Alice gemessen hat oder ob das Photon auf dem Weg zu Alice nicht irgend wo anders absorbiert wurde.

Nehmen Sie die Ergebnistabelle oben und spielen Sie es in Ruhe durch – gebnau dafür habe ich mir die Mühe ja gemacht. Dann werden Sie sehen, dass aus den Ergebnissen bei Bob allein nichts geschlossen werden kann.
#45 Dr. Webbaer
3. März 2013

@Bäker
Richtig ist aber, dass die Messergebnisse – zuvor abgesprochene Filtereinstellungen annehmend, die sich dann also jeweils gleichen – jeweils gleich ausfallen auf einzelne Proben (Photonen z.B.) bezogen.

Und wenn dem so wäre, dann wäre das ein besonderes Leistungsmerkmal eines verschränkten Systems für das sich wiederum Anwendungen finden ließen, die wiederum Anlass für eine Kontemplation im Zusammenhang mit der Information bieten würden.

Bob misst sein Photon beispeilsweise im Zustand senkrecht polarisiert. Welche Botschaft hat Alice ihm geschickt?

Vielleicht liegt hier das Missverständnis, (A hat B) oder (B hat A) keine Nachricht zukommen lassen, es geht hier wie oben geschrieben um die Eigenschaften verschränkter Systeme, und zwar vor dem Hintergrund einer möglicherweise überlichtschnell übertragenen Information (die aber beim Absender (noch) nicht vorliegt).

MFG
Dr. W
#46 David
Hannover
6. Mai 2014

Falls ihr ein “online” Experiment durchführen wollt, habe ich hier diesen Link gefunden:
https://www.didaktik.physik.uni-erlangen.de/quantumlab/index.html?/quantumlab/Verschraenkung/Grundlagen/index.html
Den Artikel finde ich interessant und gut erklärt, dennoch glaube ich, man solle selbst versuchen, um den Stoff zu assimilieren.
Damit versuche ich nun die Theorie zu verdauen.
Gruß
#47 Alderamin
28. August 2014

Kann jemand erläutern, was in diesem Experiment (Spiegel berichtete, allerdings ziemlichen Unsinn) genau passiert? Figure 1 (auf das erste Bild klicken) zeigt den Aufbau.

Ich habe soweit verstanden, dass im Kristall NL1 ein verschränktes Paar mit unterschiedlicher Frequenz erzeugt wird, von dem der längerwellige Partner das Objekt beleuchtet, der kurzwellige wird zur späteren Auswertung per Interferenzmuster auf einen anderen Weg gebracht (mittels eines frequenzabhängigen teildurchlässigen Spiegels D1). Das langwellige Licht wird nach der Wechselwirkung mit dem Objekt dann im Kristall NL2 wieder mit dem Original der Lichtquelle zusammengebracht, wobei noch einmal verschränkte Paare verschiedener Frequenz entstehen. Die niederfrequenten Photonen, unter anderem jene, die mit dem Objekt wechselwirken, werden mit dem frequenzselektiven, teildurchlässigen Spiegel D3 aussortiert, und nur ihre kurzwelligen verschränkten Partner werden mit den kurzwelligen Photonen aus D1 zur Interferenz gebracht. In dem Interferenzmuster zeigt sich das Objekt durch die Photonen der höheren Frequenz abgebildet, obwohl diese Photonen selbst nie mit dem Objekt wechselwirkten.

Was ich nicht verstehe, ist der Vorgang in NL2. Es scheint so, als ob Information von den langwelligen Photonen aus dem Pfad d auf die Photonen in Pfad e mittels Verschränkung kopiert würde, was dann die Interferenz mit c beeinflusst (vielleicht in Form einer “welcher Weg”-Information, die das Interferenzmuster an bestimmten Stellen, abhängig vom beleuchteten Objekt, zerstört). Aber eigentlich sollten doch lediglich neue Photonenpaare gebildet werden, die mit denen aus d nichts zu tun haben, und alle Photonen mit Information über das Bild am Spiegel D3 ins Nirvana geschickt werden. Eine Informationsübertragung von d nach e, wie im Spiegel-Artikel angedeutet, kann es ja nicht sein, denn mittels Verschränkung lässt sich doch keine auswertbare Information instantan übertragen (und dann wäre NL2 ja auch gar nicht nötig).

Kann jemand erläutern, was genau in NL2 mit den gestreuten Photonen aus d passiert?
#48 Alderamin
29. August 2014

@myself

Keiner, der sich berufen fühlt?

Das full paper liegt jetzt auch auf Arxiv. Mal sehen, ob ich daraus schlaue werde.

https://arxiv.org/ftp/arxiv/papers/1401/1401.4318.pdf
#49 Alderamin
29. August 2014

@myself

Mit den Erklärungen auf Seite 2-4 im Paper habe ich es, glaube ich, verstanden.

Wenn es kein Objekt gibt (Transmission T=1), dann kann ein Photon, das in Figure 1 von links herein kommt, gleichzeitig alle Wege gehen: für die kurzwelligen Partner a-c-g bzw. a-c-h, b-e-g bzw. b-e-h, für die langwelligen Partner a-d-f und b-f. Würde man Koinzidenzen von Photonen an D3 und den Sensoren bei g und h messen, könnte man daher nicht ermitteln, ob das Paar in NL1 oder NL2 entstanden ist, die “welcher Weg”-Information ist nicht ersichtlich.

Unterbricht man jedoch den Pfad d (Transmission T=0), dann würde man aus einem detektierten Photon in D3 schließen können, dass ein gleichzeitig in g bzw. h detektiertes Partnerphoton aus NL2 stammen muss, denn alle langwelligen Photonen aus NL1 werden blockiert. D.h. kurzwellige Photonen aus NL1 kommen ohne in D3 detektiertes Partnerphoton bei den Sensoren an. Man hat also eine Pfad-Information, und dann gibt es keine Interferenz an den Sensoren.

Solche langwelligen Photonen aus NL1, die in d auf eine Abschattung durch das beleuchtete Objekt treffen, verursachen also keine Interferenz bei den Sensoren, solche, die keine Abschattung in d erfahren, tun dies schon. Deswegen ergibt sich ein dem Objekt entsprechendes Muster auf den Sensoren, je nachdem wo Interferenz auftritt und wo nicht. Der Witz ist, dass die Koinzidenzdetektierung in D3 gar nicht nötig ist, es reicht, dass sie möglich wäre (das erinnert mich jetzt an die Frage, ob der Mond da ist, wenn keiner hinschaut: es scheint so zu sein, dass der Mond auch dann da ist, wenn nur einer hinschauen könnte 😉 )

Ich fragte mich gerade noch, ob man die Photonen in d auch auf einen längeren Umweg schicken könnte, um die Kausalität ein wenig zu kitzeln. Kann man aber nicht, denn durch einen Laufzeitunterschied zwischen langwelligen Photonen aus NL1 und NL2 hätte man wieder eine “welcher Weg”-Information. Oder vielleicht doch, wenn man f (aber nicht e) über einen dichroischen Spiegel auf einen gleich langen Umweg schickte. Dann käme es darauf an, wo die Koinzidenz gemessen würde. Eine Messung vor dem Umweg wäre möglich, aber auch dahinter. Da bin ich mir jetzt nicht sicher, was dabei heraus käme.
#50 MartinB
9. September 2014

Sorry für die Verzögerung – bin gerade aus dem Urlaub zurück. Mal sehen, ob ichdie Tage zeit habe, mir das anzuschauen.
#51 Alderamin
9. September 2014

@MartinB

Kein Stress. 🙂
#52 noonscoomo
Berlin
17. September 2014

Hm, ich hab da mal ein, zwei Fragen und hoffe ich stelle mich nicht zu dusselig an.
Nach allem was ich unter anderem durch möglichst aufmerksames lesen deine fantastischen Blogs gelernt habe scheint es so zu sein, dass für ein Photon, welches sich ja zwangsläufig mit Lichtgeschwindigkeit bewegen muss von uns aus gesehen eigentlich keine (eigen-)Zeit vergeht. Das heisst aber doch, dass es genau genommen an jedem Punkt auf seinem Weg gleichzeitig ist (Nur so kommen ja die Myonen bis auf die Erde).
Da verschränkte Photonen nun aber zwangsläufig vom selben Ort ausgehen bewegen die sich also (je nach Betrachter) überhaupt gar nicht voneinander weg, oder hab ich hier noch irgendwas elementar falsch verstanden? Was also eigentlich passiert ist doch, dass die beiden (Schein-) Teilchen in “Wirklichkeit” also ihrer eigenen Wirklichkeit, gar keine zwei Teilchen sind, sondern nur eines, das sich auch nicht wegbewegt, d.h. es hat noch immer einen völlig unbestimmten Spin / Impuls / oder was auch immer, nur dass es für uns wie zwei Teilchen aussieht die sich durch einen Raum bewegen, den es aus ihrer eigenen Sicht gar nicht gibt. D.h. das Teilchen entscheidet sich überhaupt gar nicht, welchen Spin (oder was auch immer) es annehmen möchte, es behält beide Spins und wir gucken nur halt von verschiedenen Richtungen, wenn man so will.
Bleibt die Frage, wie das mit verschränkten Atomen ist, deren Spin sich ja jeweils umgekehrt verhalten muss. Die bewegen sich schliesslich nicht mit Lichtgeschwindigkeit, da gilt das alles also nicht… oder doch? Hab ich nicht neulich erst gelesen, dass Materie seine (Ruhe-)Masse von Higgsfeld verliehen bekommt und sich genau genommen sehr wohl mit Lichtgeschwindigkeit bewegt, nur eben nicht vom Fleck kommt, weil es ständig mit dem Higgsfeld wechselwirkt? Wenn also sich die massebehafteten (durchs Higgsfeld scheinbar mit Masse versehenen) Elementarteilchen doch mit Lichtgeschwindigkeit bewegen, dann haben wir doch den gleichen Zustand wie oben, d.h. die sind aus ihrer Sicht an jedem Punkt auf ihrer verschlungenen Bahn gleichzeitig und damit bewegen auch die sich aus ihrer Sicht gar nicht voneinander weg, oder?
Letzte Frage, dehnt sich das Higgsfeld mit der Dehnung des Raumes eigentlich aus? Wird also evtl. das Higgsfeld irgendwann für Materie “durchsichtig” so wie einst das Universum für das Licht durchsichtig wurde und bewegt sich dann wohl alle Materie mit Lichtgeschwindigkeit, weil sie nicht mehr Wechselwirkt?
#53 MartinB
17. September 2014

@noonscoomo
Es macht einfach keinen Sinn, sich ein Eigenzeit-System für’s Photon vorzustellen; man kann das anschaulich als “Für’s Photon vergeht keine Zeit” ausdrücken, aber physikalisch wirklich sinnvoll ist das nicht.

Mir ist auch nicht ganz klar, wie dir die Tatsache, dass für das teilchen scheinbar keine Zeit vergeht, weiterhilft, wenn es um Verschränkung geht (das mit dem “wir gucken aus zwei Richtungen” habe ich nicht verstanden).

Das Higgsfeld füllt den ganzen Rauma us und hat überall denselben Wert; der ändert sich auch nicht bei der Ausdehnung (das Higgsfeld wird nicht dünner oder schwächer), sonst würden Teilchen im Laufe der Zeit ihre Masse ändern.
#54 noonscoomo
17. September 2014

Ich hätte erwartet, dass gemäss der Längenkontraktion die Entfernung zwischen den beiden verschränkten Photonen (aus ihrer Sicht) einfach null ist, denn sie bewegen sich ja mit Lichtgeschwindigkeit. Daher würde auch die spezielle Relativitätstheorie nicht verletzt, wenn das “eine” Photon dem “anderen” Photon mitteilt, welchen Zustand es eingenommen hat. Oder anders ausgedrückt, im Kristall an Ort A wird aus einem Photon zwei Photonen mit halber Frequenz, die sich voneinander entfernen, das eine nach B das andere nach C. Die Entfernung zwischen A und B bzw. A und C ist aus Sicht des Photons aber null, also auch die Entfernung zwischen B und C. Also befinden sie sich am selben Ort (aus ihrer Sicht).
Ist das blöd gedacht?

Wenn es keinen Sinn macht eine Eigenzeit für ein Photon anzunehmen, dann macht doch auch der Erklärungsversuch von Steven Giddings von der University of California keinen Sinn, warum seiner Meinung nach in schwarzen Löchern keine Information verloren geht, denn, so die Idee, wenn die Masse kollabiert und sich auf eine Singularität zusammenschrumpfen will explodiert sie _sofort_ wieder, sobald sie in die Nähe der Planck Länge kommt, nur dass wir davon nix sehen, weil es (aus unserer Sicht) wirklich sehr lange dauert. Für das schwarze Loch aber dauert das eben nicht sehr lange sondern passiert quasi sofort, da für das schwarze Loch eben die Zeit anders vergeht. Auch hier könnte man ja eigentlich sagen, das sei unsinnig, sich ein Eigenzeit System für ein schwarzes Loch vorzustellen.

Mit, “wir gucken aus zwei Richtungen” meine ich, wenn ich das Photon an Ort B und das Photon an Ort C messe habe ich (aus Sicht der Photonen) beides mal das gleiche Photon gemessen, da sich ja (aus Sicht der Photonen) beide am selben Ort befinden, also das selbe Photon sind/ist. (Mist, irgendwie taugt unsere Sprache nicht für sowas).

Woher weisst du, dass das Higgsfeld sich nicht ausdehnt? Kann doch gut sein, dass die Masse früher grösser war. Wenn das für _alle_ Materie gilt kürzt sich das doch quasi wieder raus. Aber gut, da hab ich noch nicht genug drüber nachgedacht, kann schon gut sein, dass mit der Ausdehnung des Raumes auch Higgsfeld “dazu” kommt. Entschuldige meine wenig mathematische Ausdrucksweise, ich lerne erst noch, mit der Mathematik zu hantieren, das ist leider recht viel Mühe, da brauch ich mehr Zeit für.
Und sag ruhig, wenn es nervt, wenn so blutige Laien wie ich solche Fragen stellen. Ich versuche einfach nur, mit der Absurdität umzugehen, die die aktuellen physikalischen Theorien bereithalten und dabei doch überraschend gut mit den Beobachtungen übereinstimmen 😉
#55 Alderamin
17. September 2014

@noonscoomo

Kann doch gut sein, dass die Masse früher grösser war.

Nö, denn wir haben Zeitmaschinen, die in die Vergangenheit schauen können: Teleskope. Und die sehen die Spektren weit entfernter Galaxien genau so aussehen, wie heutige Sternspektren (bis auf den Dopplereffekt). Ein sich verändernde Masse hätte tiefgreifende Auswirkungen auf die Fusionsreaktionen in einem Stern und seinen Energiehaushalt. Und ich denke, auch auf das Spektrum (z.B. die temperaturbedingte Linienbreite).
#56 noonscoomo
17. September 2014

@Alderamin
Gutes Argument, hätte ich mal schön selber drauf kommen können. Schade eigentlich. Damned.

Ich hätte mich direkt auf gemacht und die dunkle Materie damit erklärt und behauptet, dass der Effekt der dunklen Materie um so stärker zu sein scheint, je weiter eine Galaxie weg ist und dann gleich noch die beschleunigte Ausdehnung damit begründet, dass ja die Masse weniger wird.
😉
#57 MartinB
18. September 2014

@noonscoomo
Ich sehe nicht so recht, wie das mit den Photonen funktionieren soll. Aus einem Photon könen nicht einfach zwei mit halber Frequenz werden (außer in speziellen Kristallen).
Aber selbst wenn; ich kann bei der Verschränkung den Zustand des Photons ja z.B. auch auf ein anderes Objekt übertragen usw. Im Prinzip könnten zwischen der Aussendung des Photons und der Messung der Verschränkung Tausende von Umwandlungen des Zustands liegen (ich übertrage den Polarisatiionszustand des Photons auf ein Elektron, dessen Spin sich entsprechend einstellt, von dort auf ein anderes Elektron usw. – macht es dann am Ende noch irgendeinen Sinnn zu sagen, dass im “Eigensystem” des Zustands (was immer das dann sein soll) keine Zeit vergeht?)

Und du hast nicht zweimal dasselbe Photon gemessen, sondern zwei unterschiedliche Photonen (ein Photon jkann ja z.B. nicht zwei Polarisationen haben).

Ich will nicht 100% ausschließen, dass deine Idee nicht doch irgendwie hinzubiegen ist, aber ich sehe es im Moment nicht.

Zustände im Schwarzen Loch bzw. am Ereignishorizont sind ein bisschen anders gelagert – dort gibt es ein Eigensystem (man kann in ein schwarzes Loch fallen), während das Eigensystem eines Photons nicht wirklich existiert.
#58 noonscoomo
18. September 2014

@MartinB
Das mit dem Kristall war nur der Anschaulichkeit wegen.
Es ist doch aber richtig, dass ich zwei Teilchen nur verschränken kann, wenn sie sich begegnen, oder?
Was mich interessiert ist ja die Frage der Nichtlokalität, die, wenn man der Idee mit der Eigenzeit eines Teilchens, z.B. eines Photons folgen mag, kein Problem mehr ist, sofern sich das Teilchen mit Lichtgeschwindigkeit bewegt. Ich stell mir das anschaulich so vor, je schneller sich ein Teilchen bewegt, um so mehr schrumpft aus dessen Sicht der Raum in der Richtung in der es sich bewegt. Wenn es sich mit annähernd Lichtgeschwindigkeit bewegt wird der Weg von A nach B sehr kurz, bei exakt Lichtgeschwindigkeit ist der Weg gleich null weil dann der Nenner in der Lorentzkontraktion gegen unendlich geht. Das bedeutet doch aber, dass das Photon aus seiner Sicht in einem zweidimensionalen Universum existiert und dort einfach nur einen Ort hat und es sich überhaupt nicht bewegt. Der Bewegungsvektor (aus unserer Sicht) des Teilchens steht senkrecht auf der Fläche, die durch die beiden Dimensionen aufgespannt wird, in denen das Photon aus seiner Sicht existiert. Wenn sich jetzt also (aus unserer Sicht) die Bewegungspfade zweier Teilchen kreuzen, dann ist das also aus ihrer jeweils eigenen Sicht so, dass sich die beiden zweidimensionalen (ich nenn sie mal) Eigentwelten, also die beiden Flächen, sich genau so schneiden, dass die beiden Punkte genau aufeinander liegen. D.h. aus ihrer jeweils eigenen Sicht befinden sie sich am selben Ort in zwei unterschiedlichen Eigenwelten, die sich schneiden.
ich mache ein konkretes Beispiel, aus Sicht eines Photons, dass von der Sonne los fliegt in Richtung Erde und das eigentlich 8min braucht, bis es auf dein Auge trifft, existiert die Entfernung Sonne – Erde nicht und es braucht aus seiner Sicht auch keine Zeit um von der Sonne zurre Erde zu fliegen. D.h. aus Sicht des Photons befinden sich sein Ursprungsort in der Sonne und der Rezeptor in deinem Auge am selben Ort seiner zweidimensionalen Eigenwelt.
Ist das verständlich? Sprache ist so doof zu benutzen für dieses Thema.
#59 MartinB
18. September 2014

@noonscoomo
“Es ist doch aber richtig, dass ich zwei Teilchen nur verschränken kann, wenn sie sich begegnen, oder?”
Nein, ich kann auch z.B. zwei elektronen dadurch verschränken, dass ich zwischen ihnen Photonen austausche)

“wenn man der Idee mit der Eigenzeit eines Teilchens, z.B. eines Photons folgen mag”
Das Problem ist, dass die Eigenzeit eines Photons einfach nicht funktioniert – mathematisch bekomme ich eine Singularität und damit kann ich nichts mehr ausrechnen, was in der Physik schon ein Problem ist…

“Das bedeutet doch aber, dass das Photon aus seiner Sicht in einem zweidimensionalen Universum existiert und dort einfach nur einen Ort hat und es sich überhaupt nicht bewegt. ”
Ja, das habe ich schon verstanden. (Die Idee ist ja auch nicht ungewöhnlich oder abwegig.) Es ist aber eben kein Standpunkt, den man sauber in Formeln fassen kann, soweit ich sehe. Auch anschaulich ist es nicht so klar: wenn das Universum für das photon zweidimensional ist und alles auf seinem Weg gleichzeitig ist, was ist dann, wenn ich es durch eine Glasscheibe schicke, die es mit 50% Wahrscheinlichkeit absorbiert? Die “hälfte” des Photons bleibt stecken, die andere nicht, aber für das Photon gibt esjja gar keine Bewegung und die halbdurchlässige Glasscheibe hier und der Detektor bei Alpha centauri sind am “selben” Ort.

Ein ganz bisschen in diese Richtung gehen Ideen wie die twistor-Theorie:
https://de.wikipedia.org/wiki/Twistor-Theorie
da sind auch Lichtkegel die fundamentalen Objekte, nicht Raumzeitpunkte, wenn ich das richtig verstehe.

Wie gesagt, deine Idee ist nicht unsinnig oder so, aber bisher ist es niemandem gelungen, auf der Basis eine sinnvolle Theorie zu bauen, die etwas erklärt (und das wurde mit ziemlicher Sicherheit schon versucht).
#60 MartinB
18. September 2014

Noch ein Nachtrag:
Das Bild mit den lichtschnell fliegenden Elektronen, die an Punkten mit dem Higgsfeld wechselwirken, ist ja nur eine Beschreibung im Rahmen von Feynman-Diagrammen. Das tatsächliche Verhalten eines Elektrons ergibt sich ja erst durch Interferenz aller möglichen Diagramme (siehe die Teilchen-von-A-nach-B-Serie). Insofern bin ich auch von daher nicht überzeugt, dass diese Sichtweise viel nützt, um Verschränkung zu verstehen. Solange wir nicht etwas fundamental neues über den Messprozess herausfinden, ist es vielleicht einfach am besten, zu akzeptieren, dass die Welt so seltsam ist.
#61 Bilder machen ohne wirklich hinzugucken – Hier wohnen Drachen
16. Januar 2015

[…] Einer der neuesten (naja, so neu auch nicht, das paper ist vom letzten August, Dank übrigens an Alderamin) besteht darin, ein Objekt zu fotografieren, ohne das Licht, das auf das Objekt fällt, überhaupt […]
#62 Werner Feller
CH-Brunnen
5. Juni 2015

Weil die Polarisation bei der Erzeugung eines Photons festgelegt wird, haben die verschränkten Teile ebenfalls die gleiche Polarisation. Ändert man durch schräge Spiegel bei einem Teilchen die Polarisation, so wird diese Information nicht an das andere Teilchen übertragen. Deshalb kann auch keine Information übertragen werden. Wieso die Physik annimmt, dass die Polarisation eines Photons erst bei der Beobachtung festliegt, ist mir ein Rätsel.
#63 MartinB
5. Juni 2015

@Werner Feller
Offensichtlich hast du nicht ganz verstanden, wie die Verschränkung funktioniert – die Polarisation wird eben nicht einfach bei der Erzeugung festgelegt.
#64 Werner Feller
6. Juni 2015

@MartinB
Wenn Du mir Deine EMail-Adr. bekannt gibst, kann ich Dir einen Artikel zusenden, der das beweist
#65 MartinB
6. Juni 2015

Setz einfach einen Link auf den Artikel hier, dann haben alle was davon.
#66 Werner Feller
8. Juni 2015

Ok, ich werde es versuchen.
1. Photonen sind Bote-Teilchen, die Kräfte zwischen Elektronen vermitteln. Sie müssen deshalb Informationen enthalten.
2, In einem Polarisationsfilter werden 50% von unpolarisiertem Licht in polarsiertes umgewandelt. Wenn die Messanordnung oder die Beobachtung die Polarisation vorgibt, müssten alle Photonen angepasst werden. Weil nachweislich keine Dämpfung im Filter erfolgt, muss eine duale Information im unpolarisiertem Licht vorhanden sein.
3. Bei Versuchen an einer Dipolantenne zeigt sich, dass die Strahlung durch die Beschleunigung von Elektronen erzeugt wird, wobei Polarisation und Polarität durch die Richtung der Beschleunigung vorgegeben werden. Diese Information muss beim abgestrahlten Photon vorhanden sein, denn mit einer um 90° gedrehten Empfangsantenne wird kein Signal empfangen. Physiker argumentieren, dass bei Radiowellen Frequenz und Energie nicht mehr durch das plancksche Wirkungquantum gegeben seien. Weil aber tausende von Elektronen in die gleiche Richtung beschleunigt werden, summieren sich dieTeilenergien und ergeben damit eine höhere Gesamtenergie.
4. Diese Tatsachen weisen darauf hin, dass die Information in einem Photon bei der Erzeugung eingeprögt und bei der Messung oder Beobachtung höchstens festgestellt werden kann. Die Veränderung der Information eines Photons in einem Kristallgitter ist ein physikalischer Vorgang, der durch die Eingrenzung der Elektronenbeweglichkeit in eine Richtung entsteht. Grundsätzlich wird dort die duale Information der Polarität auf ein Elektron übertragen, welches seine Bewegungsrichtung mit der zusätzlichen Information der Polarisation weitergibt.
4. Licht ist keine elektromagnetische Welle, sondern ein Teilchen in einem Wahrscheinlichkeitsfeld.Die Felddimensionen werden durch einen Ort- und einen Zeitvektor vorgegeben und die Polarisation, sowie die Polarität durch eine Eigendrehung des Photons um eine Achse, die senkrecht zur Polarisationsebene steht. Ohne diese Eigenschaften kann kein Photon existieren.
Leider ist die etablierte Physik so auf die Quantenfeldtheorie fixiert, dass es praktisch keine Artikel über Wahrscheinlichkeitsfelder der Elementarteilchen gibt. Man gibt sich zufrieden, dass man nichts über die Dualität von Teilchen und Welle weiss. Man will es auch nicht wissen, denn die Verschränkung von Photonen ist heilig und Versuche, die beweisen, dass Verschränkung nur mit der eingeprägten Information der Polarität funktioniert, werden tunlichst vermieden oder gar nicht kommuniziert.
Wer mehr wissen möchte, kann die Seite Leghonia.com besuchen.
#67 MartinB
8. Juni 2015

“Ok, ich werde es versuchen.”
Warum dann die Textwand? Einfach sagen, wann und wo der Artikel erschienen ist.

“Sie müssen deshalb Informationen enthalten.”
In welchem Sinne? Jedes Quantenfeld trägt informationen.

“Weil nachweislich keine Dämpfung im Filter erfolgt, muss eine duale Information im unpolarisiertem Licht vorhanden sein.”
?Normale Polfilter filtern 50% der Lichtintensität heraus.

” Physiker argumentieren, dass bei Radiowellen Frequenz und Energie nicht mehr durch das plancksche Wirkungquantum gegeben seien. ”
Echt? Dafür hätte ich gern ne Quelle.

“sondern ein Teilchen in einem Wahrscheinlichkeitsfeld.”
Was soll ein “Wahrscheinlichkeitsfeld” sein? Sowas wie die Wellenfunktion eines Elektrons?

Ach so – da gibt es gar keinen “Artikel” (im Sinne von fachartikel), es handelt sich nur um die achthundersechsundsiebzigste Privattheorie der Art “Ich bin zwar keine Physikerin, aber ich erklär den leuten, die das zum Lebensinhalt gemacht haben, mal, wie die Welt funktioniert”? Gääähn.
#68 Werner Feller
9. Juni 2015

Schon Werner Heisenberg sagte: Wenn sich in der Physik eine neue Erkenntnis durchsetzen möchte, müssen nicht nur die Professoren, sondern auch deren Studenten aussterben.
#69 MartinB
9. Juni 2015

Oh, das Galileo-Gambit? Wie originell…

Im übrigen ist das Zitat von Planck.
#70 noonscoomo
Berlin
9. Juni 2015

@Werner Feller
“man soll nicht alles glauben, was im Internet steht” (Albert Einstein)
Mir war übrigens nicht bekannt, dass Erkenntnisse das eigene Bestreben haben, sich durchsetzen zu wollen, interessanter Gedanke.
Es mag wohl sein, dass zum Entwickeln neuer Ideen Querdenker eine wichtige und initiale Rolle spielen können. Das alleine reicht aber nicht. Irgendwann muss jemand die (wissenschaftliche) Arbeit tun.
Auch in der Physik ist es ganz einfach eine Idee zu haben (siehe unzählige posts in den Kommentaren dieses tollen Blogs). Die Idee dann aber in eine Theorie und ein mathematisches Modell zu überführen und auf Widersprüche mit bisherigen Beobachtungen zu prüfen ist alternativlos. Idealer Weise werden durch die Theorie dann Vorhersagen gemacht die von anderen Theorien nicht gemacht werden, die sich dann durch Beobachtung _anderer_ bestätigen oder widerlegen lassen. Wer das nicht kann oder will muss jemanden überzeugen das zu tun oder damit leben, dass er/sie nicht ernst genommen wird. Übrigens, wenn das Zitat stimmen würde, dann wunderte es mich sehr, dass sich Quantenphysik und Relativitätstheorie überhaupt durchsetzen konnten. Das Gegenteil ist der Fall, erst die wissenschaftliche Vorgehensweise hat das potenzial, bornierte Holzköpfe von einer “neuen” Physik zu überzeugen, die übrigens nie komplett neu ist sondern immer nur erweiternd, verbessernd oder alternativ beschreibend. Max Planck war übrigens selbst ein Student, der von Professoren die “klassische” Physik lernte und sie überzeugt vertrat und der Jahre damit zugebracht haben soll zu versuchen, das Wirkungsquantum wieder los zu werden.
#71 MartinB
9. Juni 2015

@noonscoomo
Planck hat ja sogar die Quantisierungsidee nur als Modell eingeführt und zu der Zeit nicht mal an Atome geglaubt, sondern noch die Idee der kontinuierlichen Materie vertreten. Die Idee von diskreten Schwingern war eine reine Modellierungstechnik, um die UV-Katastrophe zu vermeiden.
Das Zitat ist aber soweit ich weiß wirklich von ihm.

Zum Thema neue Gesetze finden und die Physik revolutionieren empfehle ich das hier:
https://scienceblogs.de/hier-wohnen-drachen/2011/08/13/buchersommer-r-feynman-the-character-of-physical-law-wie-man-neue-gesetze-findet/
#72 TiloS
22. September 2015

Hallo zusammen,

ich bin kein Physiker, beschäftige mich aber mit dem Thema und meine, die Gedankengänge der Verschränkung (Polarisation, gleiche Zustände, Messung) so halbwegs verstanden zu haben).
Was mich beschäftigt, euch vielleicht auch, ist die Ursache der Verschränkung.
Letztendlich können 2 Photonen nur verschränkt sein, wenn sie in irgend einer Weise miteinander verbunden sind. Da wir die Verbindung nicht sehen und da auch die direkte Wirkung eine Energieübertragung im bekannten Raum ausschließt, muss die Verbindung in einer weiteren Dimension bestehen.

Wie seht ihr das, was für eine Dimension könnte das sein? Könnte diese Dimension theoretisch auch die Zeitachse sein, oder kann man das ausschließen, und es muss eine weitere bisher unbekannte Raumdimension sein?
#73 MartinB
22. September 2015

@TiloS
“muss die Verbindung in einer weiteren Dimension bestehen.”
Nein. Nicht-lokal kann auch einfach nicht-lokal heißen.
Es gibt keinen Hinweis auf so eine weitere Dimension – das schließt sie nicht aus, aber es spricht halt nichts dafür.
In so einer weiteren Dimension müssten die Teilchen dann auch entweder am selben “ort” sein (dann wäre es aber eine andere “Art” von Dimension, denn zwei Objekte, die auf demselben Längengrad liegen, sind trotzdem voneinander entfernt) oder es müsste dort auch eine überlichtschnelle Kommunikation geben (da der Kollaps nach allem, was wir wissen, instantan erfolgt).
Ohne weitere Anhaltspunkte ist es nicht sinnvoll, da hreumzuspekulieren.
#74 TiloS
22. September 2015

Ich versuche nur bestimmte Dinge auszuschließen. Ich sehe es eher so, dass für eine überlichtschnelle Kommunikation momentan nichts spricht.
Photonen mit einer Masse von 0 (oder auch jegliche Energeiquanten mit m=0 ?) bewegen sich im Raum mit Lichtgeschwindigkeit. Alles andere mit einer größeren Masse bewegt sich langsamer.
Wenn es irgend einen theoretischen Ansatz für eine höhere Geschwindigkeit gibt, bin ich dafür offen. Den sehe ich aber nicht.

Ja, in einer weiteren Dimension müssten sich die Teilchen dann auch am selben “Ort” befinden. Und ja, das wäre dann eine andere “Art” von Dimension. Und zwar so eine Art wie sie z.B. die Zeit ist. Der “Ort” wäre dann der selbe Zeitpunkt. Deswegen meine Überlegung zur Dimension Zeit.

Sie merken, meine Devise lautet “Von mehreren möglichen Erklärungen ist die einfachste Lösung die wahrscheinlichste”.
#75 MartinB
22. September 2015

@ThiloS
“Den sehe ich aber nicht.”
Das spielt in der Physik keine Rolle. Wir suchen diejenige Beschreibung der Welt, die am besten zu unseren Reslutaten passt, in sich konsistent ist und dann noch möglichst einfach.

“Ja, in einer weiteren Dimension müssten sich die Teilchen dann auch am selben “Ort” befinden. Und”
Aber wie gsagt, nur weil wir beide uns am selben Breitengrad befinden, befinden wir uns nicht am selben Ort.
Dimension ist ein fester mathematischer Begriff – das was du meinst, ist wohl etwas anderes.
“Deswegen meine Überlegung zur Dimension Zeit.”
Aber nur weil wir beide gerade existieren, können wir trotzdem nicht kommunizieren, ohne Sachen in ein Fenster zu tippen.

Damit zwei Objekte sich direkt ohne Fernwirkung beeinflussen können, müssen *alle Koordinaten* übereinstimmen. Deswegen hilft es nicht viel, noch ne 5. Koordinate draufzusatteln und zu sagen, die stimmt überein.

“meine Devise lautet “Von mehreren möglichen Erklärungen ist die einfachste Lösung die wahrscheinlichste”.”
Nur dass deine Erklärung keine ist, sorry.

Der “Kollaps” der WF ist ja auch keine “normale” Kommunikation – es lassen sich ja z.B. keine Informationen damit übertragen.

Im übrigen geht es in der Physik eben nicht um “erklären”, sondern um “beschreiben”.
#76 TiloS
22. September 2015

Sorry dass ich hartnäckig bleibe, ich versuche auch nur möglichst plausible Beschreibungen zu finden.

“…die am besten zu unseren Reslutaten passt, in sich konsistent ist”
Eine überlichtschnelle Kommunikation ist aber gerade nicht konsistent, oder sehe ich das falsch?

“Dimension ist ein fester mathematischer Begriff – das was du meinst, ist wohl etwas anderes.”
Unser Universum, speziell die Raumzeit hat nach aktuellem Stand 3 Raum- und eine Zeit-Dimension.

“Aber wie gsagt, nur weil wir beide uns am selben Breitengrad befinden, befinden wir uns nicht am selben Ort.”
Mit unterschiedlichen Breiten- und Längengrad befinden wir uns natürlich nicht am selben Ort, räumlich müssen schon 3 Dimensionen passen. Aber die Zeit, die zwar eine Dimension der Raumzeit ist, ist trotzdem eine spezielle Dimension, in der für sich genommen Verschränkungszsenarien denkbar sind.

“Aber nur weil wir beide gerade existieren, können wir trotzdem nicht kommunizieren, ohne Sachen in ein Fenster zu tippen.”
Doch, können wir doch! Danke für dieses Argument. Und damit meine ich nicht, Sachen in ein Fenster zu tippen oder auf andere Weise Informationen zu übertragen.
Stell Dir mal ein Gedankenexperiment vor in dem wir uns treffen, unsere Uhren aufeinander abstimmen und uns dann voneinander entfernen. Irgendwann messe ich dann die Zeit indem ich auf die Uhr schaue, und, oh Wunder, ich weiß, dass es auf Deiner Uhr genauso spät ist.
Damit können wir zwar keine Informationen übertragen, aber dass kann man mit verschränkten Photonen auch nicht. In gewissem Sinne sind unsere Uhren miteinander verschränkt. Und zwar über die Dimension Zeit.
Und das Ganze geht prinzipiell nicht nur mit Uhren.

Wieso sollte dann nicht wenigsten die Zeit bei der Verschränkung eine Rolle spielen? Nur von Grundprinzip her. In dem Sinne bräuchten wir auch keine 5. Dimension, wenn die Zeit schon das Grundprinzip dafür liefert.
Eine Erklärung wäre das sowieso nicht, aber vielleicht ein Ansatz für eine Beschreibung.

Hat man eigentlich schon relativistische Effekte, speziell Zeitdilatation, bei Verschränkungen geprüft? Das könnte evtl. einen Anhaltspunkt liefern.
#77 MartinB
22. September 2015

@Thilo
“ich versuche auch nur möglichst plausible Beschreibungen zu finden.”
Das ist der falsche Ansatz. Jedenfalls dann, wenn du davon ausgehst, dass die Natur plausibel im Sinne von “Passt zu meiner alltäglichen Anschauung” sein muss. Muss sie nicht.

“Irgendwann messe ich dann die Zeit indem ich auf die Uhr schaue, und, oh Wunder, ich weiß, dass es auf Deiner Uhr genauso spät ist.”
Nein, weißt du nicht, dank Relativitätstheorie.
Und das ist ja auch in keinem Sinne Kommunikation, und unsere Uhren sind nicht verschränkt im physikalischen Sinne – egal was ich mit meiner Uhr tue, es hat auf deine keine Auswirkungem.

“Nur von Grundprinzip her. In dem Sinne bräuchten wir auch keine 5. Dimension, wenn die Zeit schon das Grundprinzip dafür liefert.”
Wie soll das gehen? Alle Objekte, die “jetzt” existieren, sind gleichzeitig, aber nur einige sind verschränkt.

“Hat man eigentlich schon relativistische Effekte, speziell Zeitdilatation, bei Verschränkungen geprüft?”
Was genau willst du da prüfen? Man hat geprüft, dass die Verschränkung überlichtschnell wirkt.

Ich sag’s nochmal: Deine Idee ist zu unscharf, um damit was anfangen zu können. Erst soll es eine Extra-Dimension sein, dann ist vielleicht auch die zeit schon die Dimension, die du suchst, aber einen Mechanismus, wie diese Extra-Dimension die verschränkung einfacher machen soll, hast du nicht. Ja, sowas kann man mal lustig spekulieren, aber es hat wirklich mit Physik nicht viel zu tun.
#78 TiloS
22. September 2015

“Passt zu meiner alltäglichen Anschauung” sein muss. Muss sie nicht.”
Spricht aber auch nichts dagegen, wenn es denn passt.

“Nein, weißt du nicht, dank Relativitätstheorie.”
Ganz ehrlich, das Argument ist schwach. Natürlich weiß ich, wie spät es auf Deiner Uhr ist, und natürlich muss die Relativitätstheorie mit berücksichtigt werden. Was glaubst Du, wie bei Satelliten die korrekten Positionsdaten ermittelt werden? Indem Uhrenvergleiche gemacht werden und indem man die relativistischen Effekte mit einrechnet. Genau so kann man es bei unserem Uhrenvergleich machen.

Es geht mir darum das Prinzip darzulegen, das bei einer Verschränkung dem gleichen Muster folgt. Und es geht mir darum die Art der Dimension aufzuzeigen, die für eine Verschränkung nötig ist.

“egal was ich mit meiner Uhr tue, es hat auf deine keine Auswirkungem”
Wenn sie korrekt arbeiten, zeigen sie beide die gleiche Zeit. Wenn ich eine Uhr physikalisch bearbeite, sind sie nicht mehr “verschränkt”. Wenngleich sie soweiso nicht im physikalischen Sinne wie Photonen verschränkt waren, dazu fehlt die Unbestimmtheit vor der Messung. Trotzdem ist die zeitliche Verbindung der beiden Uhren unbestreitbar vorhanden. Also eine Verbindung unabhängig von irgendeiner Informationsübertragung, diese Verbindung besteht allein auf der Zeitachse.
#79 MartinB
22. September 2015

@TiloS
“Genau so kann man es bei unserem Uhrenvergleich machen.”
Dann musst du aber permaent ein Signal mit mir austauschen, um zu wissen, wie ich mich bewege – das widerspricht ja genau dem, was wir beid er Verschränkung beobachten.

“das bei einer Verschränkung dem gleichen Muster folgt.”
Ist aber nicht so, s.o.

” Und es geht mir darum die Art der Dimension aufzuzeigen, die für eine Verschränkung nötig ist.”
Es gibt aber keinen Anhaltspunkt, dass irgendeine Art von “Dimension” für die Verschränkung notwendig sein soll.

“Wenn sie korrekt arbeiten, zeigen sie beide die gleiche Zeit.”
Nein, s.o.
“Wenn ich eine Uhr physikalisch bearbeite, sind sie nicht mehr “verschränkt”. ”
Das hat doch mit “Verschränkung” nichts zu tun, wo man ja einen physikalischen Unterschied sieht, wenn zwei Objekte verschränkt sind gegenüber dem Fall wo sie es nicht sind.

” Trotzdem ist die zeitliche Verbindung der beiden Uhren unbestreitbar vorhanden.”
Was soll denn eine “zeitliche Verbindung” sein? Wie soll sich die äußern? Wie kann ich messen, ob zwei beliebige Objekte “zeitlich verbunden” sind?

Es ist wirklich, wirklich wirklich keine gute Idee, Physik betreiben zu wollen, indem man eine nicht richtig ausgegorene Anchauung nimmt und dann alles so hinbiegt, dass diese Anschauung passt. Leute die das tun, haben mir inzwischen seit der Blog existiert, Dutzende geschribeen, jede mit ihrer eigenen Idee, wie die Welt funktionieren sollte, meist ähnlich unscharf wie Deine Ideen, aber durch keine Argumente davon abzubringen. Bitte gehe diesen Weg nicht – du wirst nichts erreichen und unglücklich werden. (Ein Aktuelles Beispiel findest du in der ellenlangen Diskussion beim letzten Quark-Artikel.)
#80 Dr. Webbaer
22. September 2015

@ Herr Dr. Bäker (und eine ein wenig zeitversetzte Bonusfrage, die Daten- oder die Informationsübertragung meinend vor dem Hintergrund sogenannter Verschränkung)

Wenn sich zwei Empfänger-Stationen auf einer Geraden (oder “Geraden”) im Raum befinden, in der Mitte eine Sender-Station, die geeignete verschränkte Photonengruppen jeweils Richtung dieser beiden Empfänger-Stationen, wobei die jeweilige Entfernung von der Sender-Station nicht sehr groß ist, bspw. eine Lichtsekunde, aussendet, und die beiden Empfänger-Stationen über geeignete und somit gleich eingestellte Photonenfilter jeweils denselben Code (es ergibt sich so zwingend ein Code oder es ergeben sich so zwingend auf beiden Seiten gleiche Daten) empfangen, den sie als Information nutzen [1]:
Liegt dann Informationsübertragung mit a) Lichtgeschwindigkeit vor oder b) mit doppelter Lichtgeschwindigkeit oder c) mit unendlicher Geschwindigkeit?

MFG
Dr. W

[1]
Ein derart versandter Code der (womöglich: unintelligenten) Sende-Station kann Information bedeuten, bspw. – hier wird es vielleicht schnell einsichtig -, wenn ein Gewinnspiel zwischen den beiden Empfänger-Stationen lange verabredet ist.
#81 MartinB
23. September 2015

@Wb
Mein Gott, wie oft habe ich das schon gesagt (und an Beispielen erklärt, sogar ausführlich oben im Text an Hand der Beispiel-Tabelle):
Man kann aus der Messung an nur einer Seite keinen “Code” empfangen oder etwas ähnliches, indem auf den beiden Seiten Photonenfilter irgendwie eingestellt werden.
Selbstverständlich bekommt jede Station ein Signal von der Quelle mit Lichtgeschwindigkeit, mehr Information wird hier nicht übertragen. Um die Verschränkung nachzuweisen, müssen Alice und Bob ihre gemessenen Signale auf herkömmlichen Weg vergleichen.
#82 TiloS
23. September 2015

@MartinB
Es ist schade, dass es bisher zu keiner konstruktiven Diskussion gekommen ist, was eigentlich meine Intension hier war, nicht das Präsentieren einer Theorie.
Keine Angst, unglücklich werde ich aber deswegen nicht.

Ich möchte nur nochmal die Fehler in Deiner Argumentation aufzeigen:
Meine Aussage bzgl “etwas passiert zur gleichen Zeit” oder “an bestimmten Orten herrscht die gleiche Zeit” bezieht sich nur auf den angenommenen Idealfall eines ungekrümmten Raumes. In der Realität muss man immer die relativistischen Effekte mit einrechen. Ich bin davon ausgegangen, dass das ein Physiker verinnerlicht hat. Die Raumzeit ist eine Einheit und ist immer als solche zu betrachten. Zumindest kann man nicht damit argumentieren, dass etwas aufgrund der Relativität auf einmal keine Gültigkeit mehr hat. Man muss sie nur mit beachten.

“Was soll denn eine “zeitliche Verbindung” sein? Wie soll sich die äußern? Wie kann ich messen, ob zwei beliebige Objekte “zeitlich verbunden” sind?”
In dem Sinne kann man eine zeitliche Verbindung immer mit relativistischen Formeln berechnen.
Auch wenn eine Uhr aufgrund von Massen/Geschwindigkeit nicht die gleiche Zeit wie eine andere anzeigt, so sind sie doch über eine relativistische Formel miteinander verbunden. Und wenn Dir Objekte zu unscharf sind (war nur ein Beispiel) dann nimm Zeitpunkte.
Ich brauche also nicht mal was zu messen. Ich kann also die Uhrzeit, die jetzt bei Dir herrscht, genau berechnen. Das ist die zeitliche Verbindung.

Ich habe zu keinem Zeitpunkt gesagt, dass ich weiß, wie die Welt funktioniert, oder dass ich eine fertige Theorie habe. Ich wollte nur über diese Argumente diskutieren. Dass Du aber die grundlegenden Argumente bzgl. Gleichzeitigkeit und Raumzeit, die seit Einstein anerkannt sind, nicht akzeptierst, zeigt mir, bei allem Respekt, dass Du zwar viele Sachen kennst aber einige Zusammenhänge nicht verstehst.
#83 TiloS
23. September 2015

Korrektur:
“dann nimm Zeitpunkte”
ersetzen durch:
“dann nimm Punkte im Raum”
#84 Dr. Webbaer
23. September 2015

@ Herr Dr. Bäker :

Man kann aus der Messung an nur einer Seite keinen “Code” empfangen oder etwas ähnliches, indem auf den beiden Seiten Photonenfilter irgendwie eingestellt werden.

Der Sender, der genau (sofern möglich) zwischen den beiden Emfpängern steht, sendet in beide Richtungen geeignet verschränkte Photonengruppen aus, wobei auf Seiten der Empfänger die Polarisationsfilter gleich eingestellt sind und ein Photon jeweils vom Filter absorbiert wird oder nicht.

Die Empfänger erhalten dann etwas, das sich als Code bspw. als ‘00010111‘ darstellen ließe und zudem die Sicherheit, dass die jeweils andere Station sehr zeitnah den selben Code empfängt?
(Wobei dieser (erst bei den Empfängern bereit stehende) Code dann als Information wie beschrieben (bspw. für Gewinnspiele) genutzt werden könnte?)
#85 MartinB
23. September 2015

@TiloS
“Es ist schade, dass es bisher zu keiner konstruktiven Diskussion gekommen ist,”
Es kann keine konstruktive Diskussion entstehen, weil du keine konkrete Idee hast.

” Ich bin davon ausgegangen, dass das ein Physiker verinnerlicht hat. ”
Dann macht aber deine Aussage mit den “verschränkten Uhren” wirklich gar keinen Sinn mehr. (Und die Arroganz lass mal bitte stecken…)

“Auch wenn eine Uhr aufgrund von Massen/Geschwindigkeit nicht die gleiche Zeit wie eine andere anzeigt, so sind sie doch über eine relativistische Formel miteinander verbunden.”
Was soll denn das für eine Verbindung sein? Du kannst nicht herausbekommen, was meine Uhr anzeigt, nur weil wir die mal nebeneinander gehalten haben – es sei denn, du weißt, wie ich mich bewegt habe. Und dazu müsstenw ir dann Signale austauschen…

” Dass Du aber die grundlegenden Argumente bzgl. Gleichzeitigkeit und Raumzeit, die seit Einstein anerkannt sind, nicht akzeptierst, zeigt mir, bei allem Respekt, dass Du zwar viele Sachen kennst aber einige Zusammenhänge nicht verstehst.”
ROFL. Nee, is klar. Deswegen habe ich hier auch etwa 20 oder so Artikel über die ART geschrieben, weil ich das alles nicht verstehe.

Ich habe nach wie vor kein Ahnung, was du eigentlich diskutieren willst – erst sollte es eine extra-Dimension sein, die für Verschränkung zuständig ist, dann irgendwie die zeit (weil alle Objekte irgendwie zeitlich verbunden sein sollen).

@Wb
Nein, ich werde es nicht noch einmal erklären.
#86 Dr. Webbaer
23. September 2015

@ Herr Dr. Bäker :

Es wäre schon OK, wenn das geschilderte Beispiel zur Hand nehmend erklärt werden könnte, der gemeinte physikalische Sachverhalt steht ja frei von der Esoterik und könnte schon, formalwissenschaftlich, vielleicht nagt es hier ein wenig, versucht werden aufzulösen.

MFG
Dr. W
#87 Krypto
23. September 2015

@Webbaer:
Es liegt grundsätzlich Kommunikation unter c vor, weil die Beteiligten sich vorher lokal auf die Systematik einigen und 100% der Information übermitteln.
Wenn ich Dich richtig verstanden habe, könnte ich Dir auch analog zu Deinen Gedanken eine Liste mit Informationen in die Hand drücken.
#88 Alderamin
23. September 2015

@Dr. Webbaer

Der Sender, der genau (sofern möglich) zwischen den beiden Emfpängern steht, sendet in beide Richtungen geeignet verschränkte Photonengruppen aus, wobei auf Seiten der Empfänger die Polarisationsfilter gleich eingestellt sind und ein Photon jeweils vom Filter absorbiert wird oder nicht.

Die Empfänger erhalten dann etwas, das sich als Code bspw. als ‘00010111‘ darstellen ließe und zudem die Sicherheit, dass die jeweils andere Station sehr zeitnah den selben Code empfängt?

Das wäre letztlich eine Rundum-Sendung (“Broadcast” oder “Multicast”) vom Sender an mehrere Empfänger, die nach einfacher Lichtlaufzeit die gleiche Information erhalten, aber keine Übertragung von einem Empfänger zum anderen Empfänger. Eine Informationsübertragung läge nur dann vor, wenn der eine Empfänger irgendwie das Ergebnis beim anderen Empfänger willentlich beeinflussen könnte, was er nicht kann.

Er weiß zwar, dass die andere Seite die gegenteilige Polarisation beobachten wird, die er selbst beobachtet, kann dies aber eben nicht nutzen, um eine 1/0-Information von seinem Ort aus zur anderen Seite zu senden, weil er nicht einmal beeinflussen kann, welche Polarisation er selbst beobachten wird.
#89 Noonscoomo
Berlin
25. September 2015

… aber immherhin kann man das nutzen um einen zufälligen Schlüssel für eine geheime Kommunikation zu übertragen, mit dem die beiden dann unterlichtschnell, aber sicher kommunizieren können.
Übrigens, ich las gerade eine interessante Erklärung für das Fermi-Paradoxon. Wir können das Rauschen der kosmischen Strahlung deswegen nicht von der Kommunikation von Aliens unterscheiden, weil die verschlüsselt kommunizieren und es deshalb aussieht, wie Rauschen.
#90 Krypto
25. September 2015

@Noonscoomo:
Verschlüsselte Kommunikation kann man eigentlich grundsätzlich von Rauschen unterscheiden, weil es zum Einen erkennbare Protokolle geben müsste und zum Anderen ein gewisser Signal/Rauschabstand eingehalten werden muss, damit Aliens ihr Signal vom Rauschen unterscheiden können.
Sonst hätten bei uns Geheimdienste leichtes Spiel, wenn sie Ihre Kommunikation im starken irdischen Rauschen verstecken könnten.
#91 Dr. Webbaer
25. September 2015

@ Alderamin :

Das wäre letztlich eine Rundum-Sendung (“Broadcast” oder “Multicast”) vom Sender an mehrere Empfänger, die nach einfacher Lichtlaufzeit die gleiche Information erhalten, aber keine Übertragung von einem Empfänger zum anderen Empfänger.

Negativ, natürlich nicht!, weil die Daten erst bei den jeweiligen Empfängerstationen erhoben werden können, sich der Gleichheit der Daten, die jeweils andere Empfängerstation meinend, sicher, wobei diese Daten idF und vorab verabredeten Kodierungsregeln folgend zu Information bestimmt werden könnten.
Eben bspw. ‘Gewinnspiele’ (siehe oben) meinend oder für die Zwecke symmetrischer Verschlüsselung.

@ Krypto:
Dito.

MFG
Dr. W
#92 Alderamin
25. September 2015

@Dr. Webbaer

Negativ, natürlich nicht!

Oh wohl! Informationsübertragung ist, wenn ich ein Bit (nicht das Bier…) habe und es einem Empfänger über einen Kanal zu diesem mitteile. Wenn mir meine Tante erzählt, sie sendet mir und meiner Schwester eine Tafel Schokolade oder eine Tüte Bonbons, kann sich aber noch nicht entscheiden, wem sie was sendet, dann ist es keine Informationsübertragung von meiner Schwester zu mir, wenn ich beim Auspacken des Geschenks aus meiner Schokolade auf ihre Bonbons schließe. Es besteht ja nicht einmal ein Kommunikaitonskanal zwischen uns. Vielleicht hat sie die Schokolade ja auch gar nicht erhalten, und der Postbote hat sie gegessen. Vielleicht wusste sie gar nicht, was es zu verteilen gab (und ob es überhaupt etwas gab).

Bestenfalls wäre es eine Informationsübertraung von meiner Tante zu jedem von uns beiden. Ich hatte übrigens unter anderem Informationstheorie in der Promotionsprüfung, falls das Eindruck macht 😛
#93 Alderamin
25. September 2015

@myself

Vielleicht hat sie die Schokolade ja auch gar nicht erhalten, und der Postbote hat sie gegessen.

Äh, Bonbons natürlich… (aber die Radlermaß eben war lecker…)
#94 Dr. Webbaer
26. September 2015

@ Alderamin :

Das wäre letztlich eine Rundum-Sendung (“Broadcast” oder “Multicast”) vom Sender an mehrere Empfänger, die nach einfacher Lichtlaufzeit die gleiche Information erhalten, aber keine Übertragung von einem Empfänger zum anderen Empfänger. [Alderamin]

Negativ, natürlich nicht!, weil die Daten erst bei den jeweiligen Empfängerstationen erhoben werden können, sich der Gleichheit der Daten, die jeweils andere Empfängerstation meinend, sicher, wobei diese Daten idF und vorab verabredeten Kodierungsregeln folgend zu Information bestimmt werden könnten.

Oh wohl! Informationsübertragung ist, wenn ich ein Bit (nicht das Bier…) habe und es einem Empfänger über einen Kanal zu diesem mitteile.

Negativ, das wäre Datenübertragung.
Information hat Bedeutung.
Information wird für Transportzwecke vom Sender kodiert und beim Empfänger dekodiert bzw. abstrahiert, wiederum zu Information.
Information kann aber auch von erkennenden Subjekten geschöpft werden, bspw. wäre eine neue wissenschaftliche Theorie von Individuen oder Gruppen geschöpft.
Die Frage ist wie die im Beispiel geschilderte Schöpfung von Information genau verstanden werden kann, den Transport des geschilderten Kanals betreffend.
Ansonsten wurde Ihr Kommentatorenfreund nicht ganz schlau, aus dem was Sie geschrieben haben.
Sie dürfen gerne davon ausgehen, dass Dr. Webbaer (auch) bei diesem Thema halbwegs firm ist.

MFG
Dr. W (der hofft, dass die verwendeten HTML-Auszeichnungen korrekte visuelle Ausgabe bewirken werden)
#95 Dr. Webbaer
26. September 2015

OK, zuviele BLOCKQUOTEs verschachtelt, so müsste es klappen:

@ Alderamin :

Das wäre letztlich eine Rundum-Sendung (“Broadcast” oder “Multicast”) vom Sender an mehrere Empfänger, die nach einfacher Lichtlaufzeit die gleiche Information erhalten, aber keine Übertragung von einem Empfänger zum anderen Empfänger. [Alderamin]

Negativ, natürlich nicht!, weil die Daten erst bei den jeweiligen Empfängerstationen erhoben werden können, sich der Gleichheit der Daten, die jeweils andere Empfängerstation meinend, sicher, wobei diese Daten idF und vorab verabredeten Kodierungsregeln folgend zu Information bestimmt werden könnten. [Dr. Webbaer]

Oh wohl! Informationsübertragung ist, wenn ich ein Bit (nicht das Bier…) habe und es einem Empfänger über einen Kanal zu diesem mitteile. [Alderamin]

Negativ, das wäre Datenübertragung.
Information hat Bedeutung.
Information wird für Transportzwecke vom Sender kodiert und beim Empfänger dekodiert bzw. abstrahiert, wiederum zu Information.
Information kann aber auch von erkennenden Subjekten geschöpft werden, bspw. wäre eine neue wissenschaftliche Theorie von Individuen oder Gruppen geschöpft.
Die Frage ist wie die im Beispiel geschilderte Schöpfung von Information genau verstanden werden kann, den Transport des geschilderten Kanals betreffend.
Ansonsten wurde Ihr Kommentatorenfreund nicht ganz schlau, aus dem was Sie geschrieben haben.
Sie dürfen gerne davon ausgehen, dass Dr. Webbaer (auch) bei diesem Thema halbwegs firm ist.

MFG
Dr. W
#96 Uwe
Hamurg
10. Februar 2016

Hallo MB,
habe Deine obigen Ausführungen nur überflogen. Auch wenn ich den mathematischen Teil nahezu ausgelassen habe, erscheint mir Deine Darstellung als pädagogisch sehr verständlich und wertvoll für Leute wie mich, die sich damit nachts hobbymäßig auseinandersetzen und gleich wieder arbeiten müssen. Verschränkung – ein wohl noch für lange Zeit elementares Thema in der Physik. Habe ich das richtig verstanden: Entweder beide Photonen (ungemessen laut Prof. H. Lensch und Schrödinger, Heisenberg dann eigentlich Wellen) werden bei dem Messvorgang registriert, oder keines, auch bei unterschiedlicher Polfilterstellung – gelten also dann als verschränkt? Ich weiß, der Diskurs kann noch viel komplexer werden, angefangen bei der Aufspaltung des Laserstrahls etc..

Aber bitte einfache Antworten – hab´s nur bis zur speziellen Relativitätstheorie geschafft (mathematisch, und das ist auch schon eine Weile her – hab gerade nicht mal mehr die Lorentz-Transformation herleiten können). War von Haus aus (Studium) Wissenschaftstheoretiker und versuche, auf dem Laufenden zu bleiben.

Beste Grüße
Uwe Schubert
#97 MartinB
10. Februar 2016

Hallo Uwe,
“Entweder beide Photonen (ungemessen laut Prof. H. Lensch und Schrödinger, Heisenberg dann eigentlich Wellen) werden bei dem Messvorgang registriert, oder keines, auch bei unterschiedlicher Polfilterstellung”
Nein, siehe auch die Beispieltabelle, wo Alice und Bob ihre Ergebnisse vergleichen.
Du musst immer den Zustand anschauen und dann die Regel anwenden: Wenn eine einen Zustand misst, dann ist der Zustand bei der anderen der, der als Faktor daneben steht.
Also: Wenn ich z.B. (rauf-rauf)+(runter-runter) habe und Alice misst rauf, dann muss das Photon bei Bob auch im Zustand rauf sein. Ob er es dann misst und mit welcher Wahrscheinlichkeit, hängt von der Stellung seines Polfilters ab.
#98 Wolfgang Voß
58638 Iserlohn
25. Dezember 2016

Hallo Herr Bäker,

Ich habe heute Ihren Block gelesen.
Leider gibt es da einige Dinge die sich mir nicht eschließen.

Sie schreiben dass ein senkrecht polarisiertes Photon einen Polarisationsfilter der dazu um 45° verdreht ist mit einer Wahrscheinlichkeit von 50% passiert.

Das hört sich für mich nach Zufallsgenerator an.

Wenn es tatsächlich rein zufällig den Filter passiert, so müsste bei einem nachfolgenden zweiten Polarisationsfilter wiederum die Hälfte der noch vorhandenen Photonen herausgefiltert werden.

Das würde bedeuten, dass es letztlich vom Aufbau (Dicke) des Filters abhängt verfiele Photonen bei einer Verdrehung von 45% den Filter passieren.

Kann es sein, dass die Phasenlage der Schwingung eines Photons, beim Erreichen des Filters mit beeinflusst, ob der Filter Passiert werden kann oder nicht und es somit nicht wirklich zufällig passiert?
#99 Aveneer
7. Februar 2018

>also nicht verzweifeln, wenn ihr nicht auf Anhieb seht, wie’s geht.
Hallo Martin – (Nicht denken der schon wieder.) Ist, denke ich, nicht schlimm was nun kommt. Nur ein Ansatz, der das „belegen“ soll, was du sagst.
5 Jahre – ich hoffe es hat gereicht. Meine Interpretation ist (hoffe ich) eher aus dem Satz von Bayes (Bayes Theorem) abgleitet.
Bob und Alice kennen sich in der QM aus und überlegen sich zuerst, eine sogenannte priori-Wahrscheinlichkeit (“priors”) von dem was sie messen werden. Dann überprüfen sie diese Überlegung.

Alice und Bob messen simultan an zwei verschiedenen Orten. Simultan bedeutet doch auch, dass die beiden Ergebnisse den maximalen raumzeitlichen Abstand haben (ignorier den Satz, wenn er falsch ist). Alice kann sich daher z.B. nicht sicher sein, das Bob gemessen hat. Der zeitliche Abstand der Information – Bob hat auch gemessen – ist bei simultaner Messung maximal (ich denke das ist wichtig). Die Unsicherheit, dass Bob die erwartete Messung auch durchgeführt hat maximal. Das Bedeutet, dass eine einzelne Messung von Alice gar keine Information über den Zustand bei Bob enthält. Vielleicht war er „schnell“ auf Toilette. Sieht Sie nicht, da der Abstand „Sonne / Erde“ entspricht- da ist das schon mal drin. Oder sein Photon ist daneben vorbei gefolgen…Sie müssen daher viele male Messen um die zuvor definierte priori-Wahrscheinlichkeit zu finden. Und sie wird erst so richtig “real” wenn sie ihre Messprotokolle mit max. c versenden um zu erkennen, dass jeder gemessen hat.

Was ich sagen möchte, bei einer simultanen Messung trägt das Messerergebnis an beiden Orten eigentlich gar keine Information, sie müssen auf „das Licht“ warten, die ihnen zeigt, ob der andere tatsächlich gemessen hat. Bei simultanen Messung hat die einzelne Messung ein „degree of belief“ von 0. Schöner wär‘s man würde erst sehen, dass der andere auch misst – dann wäre es aber nicht mehr überraschend sozusagen ~ „100%“ vorhersagbar.

Kann man das so sagen? Ich finde es eine recht gute Beschreibung, warum keine Information im eigentlichen Sinn übertragen wird (weil die Unsicherheit maximal ist- “Null” information) und warum man mehrmals messen muss.

Gruß
Aveneer
#100 MartinB
7. Februar 2018

Ich vermuzte, das ist einigermaßen richtig, aber so ganz verstehe ich nicht, was du schreibst.
Richtig ist auf jeden Fall, dass beide Daten normal austauschenmüssen, um die Verschränkung zu sehen.
#101 Lulu
Berlin
15. Dezember 2018

Die Nichtlokalität ist irgendwie vorstellbarer, wenn man sich dazu denkt, dass das Photon keine Eigenzeit hat, aber die Verschränkung gibt es auch mit langsameren Teilchen, oder?
#102 Wolfgang Stegemann
Bad Iburg
13. Februar 2019

Frage, es heißt Verschrnkungen funktionieren über Entfernungen von Lichtjahren hinweg. Wie will man das denn messen?
#103 MartinB
14. Februar 2019

Naja, gemessen hat man das über Entfernungen von vielen Kilometern, aber so, dass man sich sicher ist, dass zwischen beiden Messungen kein Signal mit Lichtgeschwindigkeit hätte ausgetauscht werden können.
Wenn das klappt, dann klappt es auch über Lichtjahre, auch wenn man das direkt nicht messen kann.
#104 Wolfgang Stegemann
Bad Iburg
14. Februar 2019

Das ist aber nicht überzeugend. Gedankenexperiment: angenommen zwei verschränkte Teilchen ziehen eine Spur von Teilchen hinter sich her, die man noch nicht wahrnehmen kann und die die Verbindung ausmacht, und diese Spur ist nur 200 km lang, dann endet die spukhafte Fernwirkung nach 200 km. Also wäre alles andere eine falsifizierte Theorie.
#105 Wolfgang Stegemann
Bad Iburg
14. Februar 2019

In einem anderen Forum wird grade gesagt, daß die Verschränkung mit der Messung aufhört, man also ein Teilchen hier manipulieren kann, das ursprünglich verschränkte dann aber nicht mehr reagiert. Stimmt das?
#106 MartinB
14. Februar 2019

@Wolfgang
Klar kann man immer annehmen, dass genau hinter dem Bereich, wo wir gerade aufhören zu messen, plötzlich was ganz Neues passiert. Es gibt nur keinen Hinweis darauf und die Konsistenz unserer Theorien lässt es sehr unwahrscheinlich erscheinen, aber zu 100% wissen kann man es nicht.

“daß die Verschränkung mit der Messung aufhört, ”
das ist so ungenau formuliert, dass ich die Richtigkeit nicht beurteilen mag. Wenn ich die Verschränkte Eigenschaft eines Objekts messe, dann ist hinterher diese Eigenschaft nicht mehr verschränkt – habe ich zwei Photonen mit verschränkter Polarisation, dann ist die Verschränkung nicht mehr da, sobald ich eine der beiden Polarisationen vollständig bestimmt habe, das ist richtig.
#107 Wolfgang Stegemann
Bad Iburg
14. Februar 2019

Noch eine letzte Frage: warum nimmt man nicht einfach an, daß es zwischen zwei verschränkten Teilchen eine Verbindung gibt (ein Quantensystem), daß man die Verbindung nur (noch) nicht kennt. Dann wäre alles einfach und man würde sich die gedanklichen Verrenkungen sparen.
#108 MartinB
https://scienceblogs.de/hier-wohnen-drachen
14. Februar 2019

Kann man machen, die müsste halt nur überlichtschnell sein und die Relativitätstheorie verletzen. Man könnte zum Beispiel nicht sagen, welche von zwei messungen zuerst ist, also kann man auch nicht sagen, wie sich da etwas ausbreiten soll (siehe dazu meinen Artikel Quantenmechanik und Realität, rechts bei den Serien zu finden).
Insofern macht das die Sache nicht wirklich besser.
#109 S.Steinmeyer
Rauenberg
6. Mai 2020

Super Artikelserie, auf die ich leider erst spät gestoßen bin. Bleibe dem Blog ab jetzt sicher treu! Allerdings habe ich mit diesem dritten Teil ein Problem. Alles ist gut bis zu dem Moment, an dem plötzlich der Zustand
\[\frac{1}{\sqrt{2}} |\uparrow\rangle |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle |\rightarrow\rangle\]

vom Hinmmel fällt. Wo kommt der denn jetzt her? Wie ensteht er aus den beiden unter -45° polarisierten Photonen? Tut er das überhaupt? Keine Ahnung, er taucht einfach aus dem Nichts auf. Da könnte ja jeder kommen und irgendeinen Zustand erfinden (Scherz).
Da er aber nun mal der grundlegende Ausgangspunkt für alle weiteren Erklärungen zur Verschränkung ist, empfinde ich es als äußerst unbefriedigend ihn nicht herleiten oder nachvollziehen zu können. Können sie mit bitte helfen? Das wäre großartig!
#110 MartinB
6. Mai 2020

@S. Steinmeyer
Das habe ich in diesem Artikel auch gar nicht erklärt. Was der Zustand ja tut ist, dass beide Photonen immer dieselbe Polarisation haben (egal welche das ist). Man braucht also einen Prozess, der zwei Photonen so erzeugt, dass ihre Polarisation identisch (aber unbekannt) ist.
Eine Möglichkeit dazu ist das hier:
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
#111 S.Steinmeyer
Rauenberg
6. Mai 2020

Die Antwort kam aber schnell! Danke dafür. Es ist also einfach nur ein Zustand, der die gewünschte Verschränkung beschreibt. ok. Damit verstehe ich jetzt auch den Rest. Nur eine weitere Aussage ist mir noch unklar. Ein paar Zeien weiter unten steht, dass das rechte Photon, für sich alleine betrachtet, vor der Messung im Zustand \frac{1}{\sqrt{2}} |\uparrow\rangle + \frac{1}{\sqrt{2}} |\rightarrow\rangle, war. Woher weiß ich denn dass es vorher genau in diesem Zustand war? Das kann ich doch aus dem “gebauten” Zustand nicht ablesen, oder? Sorry, wenn ich da auf dem Schlauch stehe.
#112 MartinB
7. Mai 2020

Wenn ich gar nicht wüsste, dass die Photonen verschränkt sind, dann weiß ich nichts über das linke Photon, dann schaue ich mir nur die Terme für das rechte Photon an, die anderen ignoriere ich schlicht. Das rechte Photon hat dieselbe Wahrscheinlichkeit für rauf und rechts, das ist sein Zustand. Dass es mit dem linken Photon verschränkt ist, weiß ich ja nicht, wenn ich nur das rechte habe.
#113 S.Steinmeyer
Rauenberg
7. Mai 2020

Das rechte Photon hat dieselbe Wahrscheinlichkeit für rauf und rechts, das ist sein Zustand.

Genau das verstehe ich ja nicht. Woher weiß ich, dass es z.B. nicht im Zustand mit der Wahrscheinlichkeit 50% -45° und 50% +45° ist?
Ist es etwa so, dass der Zustand den wir uns “gebaut” haben (und somit das ganze Beispiel), auf der Annahme basiert, dass die Photonen (in unverschränktem Zustand, also nur für sich alleine genommen) jeweils unter -45° (und damit mit 50% jeweils für rauf und rechts) polarisiert sind?
#114 MartinB
7. Mai 2020

@S.Steinmeyer
Das wäre ja (rechne es nach) derselbe Zustand.
Letztlich ist der Zustand einfach so, dass jede Polarisation gleich wahrscheinlich ist, egal wie ich die beiden Achsen wähle entlang derer ich die Polarisation angebe,

Jedes Photon für sich ist in der Polarisation vollkommen unbestimmt, aber beide haben immer dieselbe Polarisation, wenn man misst.
#115 Thomas Kretschmer
Berlin
19. Februar 2021

Guten Tag, MartinB,
ist die irgendeine Veröffentlichung bekannt, nach der verschränkte Photonen geringere Transmissionsgrade für Polfilter oder Polarisationswürfel haben, als unverschränkte, gleichermaßen Reflexionsgrade?
#116 MartinB
20. Februar 2021

@Thomas
Nein, das kann wenn ich die Frage richtig verstehe, auch so nicht sein. Man kann ja immer lokal das möglicherweise irgendwo existierende verschränkte andere Teilchen ignorieren.
#117 Thomas Kretschmer
Berlin
22. Februar 2021

MartinB,
vielen Dank für die Antwort. Ich bekomme aber andere Ergebnisse. Daher suche ich noch ein bisschen nach solchen Untersuchungen und erarbeite einen Vorschlag, wie das feststellbar sein müsste. Viele Grüße Thomas
#118 MartinB
23. Februar 2021

@Thomas
“Ich bekomme aber andere Ergebnisse.”
Dann machst du mit 99,999%-iger Sicherheit irgendwo einen Denkfehler (oder ich verstehe die Frage falsch). Kenne ich zur Genüge, ich habe in den letzten paar Monaten mehrfach die Quantenmechanik “widerlegt” – hat jeweils ne Weile gedauert, bis ich meinen Denkfehler bemerkt habe.
#119 Thomas Kretschmer
Berlin
23. Februar 2021

also, wenn du hinten vielleicht ein paar Neunen wegstreichst, wäre es charmanter. Nur und wirklich nur wenn es dich interessiert, schau mal da:
https://www.researchgate.net/post/Have_entangled_photons_a_lower_polarizing-filter-transmittance_than_unentangled_photons
(100% Bell-konform und ohne Zusatzstoffe)
#120 Julian S.
15. März 2021

Hallo zusammen,
ich habe folgende Frage zu der letzten Abbildung auf der ersten Seite:
Warum wurden in der Darstellung die “Gitterstreben” vom Polfilter horizontal gezeichnet, obwohl die Richtung vom Filter vertikal ist? Ich frage mich wie ich erklären kann, dass trotz der horizontal dargestellten “Gitterstreben” eine vertikale Welle hindurchkommt.

P.S.: Vielen Dank für den großartig geschriebenen Artikel!
#121 noonscoomo
Berlin
15. März 2021

Kurz gesagt liegt das daran, dass so eine Welle von etwas, was elektrisch leitend ist dann am besten absorbiert wird, wenn es parallel zu der Welle ist. Wenn es also entlang der Richtung des Leiters schwingt, dann entsteht in dem Leiter ein Stromfluss und der wird durch den Widerstand zu Wärme. Wenn die Welle jetzt genau senkrecht zu dem Gitter daher kommt, dann wird da in nem kleinen Stück des Querschnitts des Leiters kein Strom induziert und die Welle geht ungehindert durch.
#122 MartinB
16. März 2021

Stell dir die Drähte wie kleine, eindimensionale Spiegel vor. Licht, dass entlang der Drähte schwingt, kann reflektiert werden (weil die Elektronen in den Drähten im Licht mitschwingen und eine elektromagnetische Welle aussenden, die mit der einfallenden Welle wechselwirkt und sie aufhebt), Licht, das senkrecht dazu schwingt dagegen nicht, weil die Elektronen in ihrem jeweiligen Draht gefangen sind.

Meistens zeichnet man die Linien auf Polfilter allerdings tatsächlich in Durchlassrichtung.

Quantenmechanik verstehen III – Verschränkung

Kommentare (122)

Neueste Beiträge

So long and thanks for all the fun: Hier wohnen Drachen zieht um!

Kurz notiert: Nein, niemand hat ein Wurmloch gebaut

Quantenverschränkung für Anfänger: Der Physik-Nobelpreis 2022

Prehistoric Planet – ein Traum wird wahr!

Die Parabel von Achilles und der Schildkröte

Letzte Kommentare

Über das Blog

Artikelserien

Bücher

Archive

Meta

Quantenmechanik verstehen III – Verschränkung

Kommentare (122)

Abonnieren

Neueste Beiträge

So long and thanks for all the fun: Hier wohnen Drachen zieht um!

Kurz notiert: Nein, niemand hat ein Wurmloch gebaut

Quantenverschränkung für Anfänger: Der Physik-Nobelpreis 2022

Prehistoric Planet – ein Traum wird wahr!

Die Parabel von Achilles und der Schildkröte

Letzte Kommentare

Über das Blog

Artikelserien

Bücher

Schlagwörter

Archive

Meta