Von NOAA / National Weather Service – National Centers for Environmental Prediction – Climate Prediction Center
File: W!B: (overlay of weeks, see below) – www.nws.noaa.gov > Monitoring & Data > Global Climate Data > Global Regional Climate Maps > Europe [1], Gemeinfrei, Link
Die Temperatur ist eine Größe, die an jedem Punkt in Europa einen Wert hat – deswegen spricht man auch von einem Temperaturfeld.
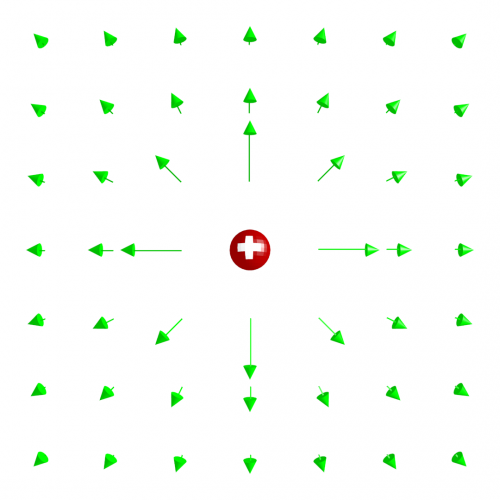
Ein anderes Beispiel ist ein elektrisches Feld – beispielsweise das elektrische Feld einer Punktladung (hier in zwei Dimensionen gezeichnet, damit es übersichtlicher ist):
Die Länge des Pfeils sagt, wie stark das Feld ist, die Richtung des Pfeils sagt, in welche Richtung das Feld zeigt. Natürlich kann ich das Feld nicht wirklich an jedem Punkt zeichnen, weil man dann nichts mehr erkennt, aber das Feld hat an jedem Punkt einen Wert.
Licht ist ja eine elektromagnetische Welle, man kann es deshalb (in der klassischen Physik) dadurch beschreiben, dass man an jedem Punkt im Raum und zu jedem Zeitpunkt sagt, wie groß jeweils der Wert des elektrischen und des magnetischen Feldes ist. (Tatsächlich benutzen die Physikerinnen meist eine andere Größe, das Viererpotential, weil das mathematisch einfacher ist, besonders in der QFT, aber mit dieser Komplikation ärgern wir uns hier nicht herum.)
Ähnliches gilt auch für Objekte wie Elektronen. Wir stellen uns Elektronen ja gern als kleine Kugeln vor (so wie die rote Kugel oben im Bild, nur dass die positiv geladen ist, nicht negativ – negativ geladene Teilchen sind natürlich blau, nicht rot). In der klassischen Physik ist das auch ein richtiges Bild, aber in der Feldtheorie beschreibt man ein Elektron nicht mehr als ein Teilchen, das sich an einem bestimmten Ort aufhält, sondern als Elektronenfeld – dieses Feld hat an jedem Punkt des Raumes einen Wert. Wenn ich weiß, dass sich ein einzelnes Elektron in einem kleinen Kasten aufhält, dann ist der Wert dieses Feldes im Kasten entsprechend ungleich Null, außerhalb gleich Null – jedenfalls wäre es bei einem “klassichen” Elektronenfeld so.
Hier kann man sich leicht verwirren lassen: Um das Vakuum quantentheoretisch beschreiben zu können, braucht man eine Quantenfeldtheorie. Was ich hier im Moment habe, ist noch eine klassische Feldtheorie, in der hat das Feld (wie ein Elektronenfeld oder ein elektrisches Feld) an jedem Punkt einen eindeutigen Wert, und wenn das Elektron “hier” ist, dann ist der Wert dieses Feldes überall woanders exakt gleich Null.
Leute, die schon etwas über Quantenmechanik wissen, sollten dieses Elektronenfeld auf keinen Fall mit der Elektronenwellenfunktion in der Quantenmechanik verwechseln – die beschreibt ein einzelnes Elektron quantenmechanisch, aber sie beschreibt nicht das Elektronfeld. Das Elektronfeld ist hier noch ein klassisches Feld (auch nicht ganz, 
weil es ein Spinorfeld ist, das erst quantisiert werden muss – eine echte klassische Theorie für das Elektron gibt es – anders als beim elektromagnetischen Feld – nicht.) Das wird oft verwirrend dargestellt – detailliert habe ich das hier erklärt.
Man könnte jetzt meinen, damit sei die Sache mit dem Vakuum ja wieder etwas einfacher geworden: Wenn alles durch solche Felder beschrieben werden kann, dann kann ich einfach sagen “Vakuum ist ein feldfreier Raum.” Im Vakuum ist der Wert des Feldes immer überall Null, und zwar für alle Felder, die es gibt (das elektrische und magnetische, das Elektronfeld und jedes andere Feld für all die anderen Elementarteilchen wie Quarks und Neutrinos ebenfalls). Das ist aber nicht richtig – bisher haben wir zwar Felder, aber wir haben die noch nicht mit den Mitteln der Quantentheorie beschrieben, das tun wir jetzt.
Quantenmechanische Überlagerungen
O.k., wir haben also jetzt ein Elektronfeld (oder ein elektromagnetisches Feld), das an jedem Punkt im Raum einen Wert hat. Damit sind wir aber noch nicht in der Quantentheorie angekommen – in der Quantentheorie haben Felder nämlich meist keine eindeutigen Werte, sondern befinden sich in Überlagerungszuständen. (Der Link erklärt dasmit der Überlagerung ausführlich, hier die Kurzfassung.)
![[1]](https://www.cpc.ncep.noaa.gov/products/analysis_monitoring/regional_monitoring/wcmax1.png){kind=link}
Kommentare (97)