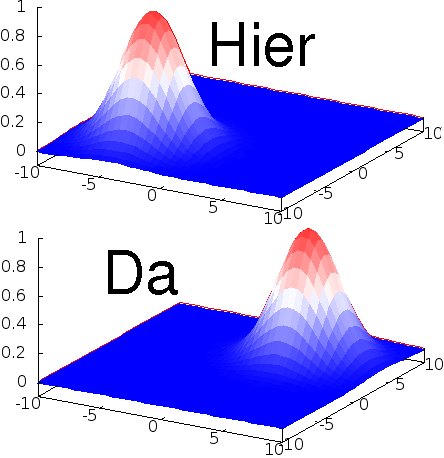
In der Quantentheorie kann man – außer wenn man gerade eine Messung gemacht hat und damit ganz sicher weiß, was los ist – nur Wahrscheinlichkeiten dafür angeben, dass ein System in einem bestimmten Zustand ist. Beispielsweise könnte ein Elektron entweder “hier” oder “da” sein – wenn es “hier” ist, dann hat das Elektronfeld einen großen Wert “hier”, wenn es “da” ist, hat es einen großen Wert “da”.
Da
s Bild ist etwas vereinfacht, weil das Elektron ja einen Spin hat, den ignoriere ich hier – ansonsten müsste das feld mehrere Spinorkomponenten haben, das wäre erstens unübersichtlich und ändert zweitens nichts am Prinzip.)
Wichtig ist hier, dass das Quantenfeld nicht einfach die Summe aus beiden Feldern ist. Vielmehr muss man für jede der beiden Möglichkeiten eine eigene Wahrscheinlichkeit angeben, die beiden Möglichkeiten sind aber zu unterscheiden. Wenn euch das verwirrt, denkt nochmal an das Temperaturfeld. Wenn es eine 50%-Wahrscheinlichkeit dafür gibt, dass morgen in Braunschweig 30° (freu) sind und 50% Wahrscheinlichkeit für 20° (kaaalt), dann ist das nicht dasselbe als wenn die Temperatur morgen 50° (oder 25°, wegen der 50%) ist, oder? Quantenmechanische Wahrscheinlichkeiten verhalten sich genauso, auch wenn sie – anders als beim Wetter – nicht einfach nur dadurch kommen, dass wir etwas nicht wissen.
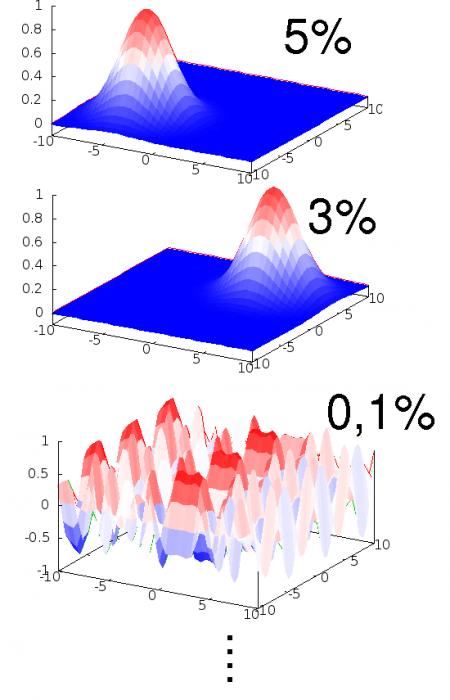
Um den Zustand eines Feldes (beispielsweise des elektrischen Feldes oder des Elektronfeldes) in der QFT anzugeben, muss ich jetzt für alle möglichen Felder die Wahrscheinlichkeit angeben:
Mathematisch ist das ziemlich trickreich, weil es ja unendlich viele mögliche Funktionen gibt, die das Feld beschreiben können. Deswegen wird das genau so auch selten tatsächlich gemacht, sondern sich mit anderen Techniken (wie dem Pfadintegral oder der “kanonischen Quantisierung”) beholfen.
Also: Um einen Zustand eines Quantenfeldes anzugeben, müsst ihr alle möglichen Feldkonfigurationen hinschreiben und für jede davon eine Wahrscheinlichkeit angeben.
Ich habe mal wieder etwas vereinfacht,- genauer gesagt muss man für jede Feldkonfiguration nicht die Wahrscheinlichkeit, sondern die Wahrscheinlichkeitsamplitude angeben, die eine komplexe Zahl ist. Aber hier geht’s ja nur ums Prinzip, nicht um die Details. Außerdem habe ich etwas übertrieben: es reicht, wenn ihr einen vollständigen Satz von Feldkonfigurationen betrachtet also beispielsweise alle Fourierkomponenten. Das ist ähnlich in der Quantenmechanik – dort ist der Zustand eindeutig bestimmt, wenn ihr die Wahrscheinlichkeit für jeden mögliche Ort des Elektrons angebt, das ist dann gerade die Wellenfunktion. Aber Achtung: Es bekommt nicht einfach bloß die Fourierkomponente zur Wellenzahl k eine einzige Amplitude, sondern jeder mögliche Wert der Fourierkomponente hat eine Wahrscheinlichkeitsamplitude. Im Detail habe ich das auch in der QFT-Serie in den letzten beiden Teilen zum Thema Zustände erklärt.
Das Vakuum
Man könnte jetzt annehmen, dass der Vakuumzustand derjenige ist, bei dem die Wahrscheinlichkeit, dass unser Quantenfeld (wir betrachten erst mal nur ein Feld, beispielsweise das elektromagntische) überall gleich Null ist, gleich 1 ist und alle anderen Zustände, in denen das Feld irgendwo von Null verschieden ist, haben den Wert Null. Das sollte doch die beste Annäherung an die Idee des “feldfreien Raums” sein, oder? Das sähe etwa so aus:
Es gibt da nur ein klitzekleines Problem: Wenn ihr die Gleichungen der QFT verwendet, um diesen Zustand zu berechnen, dann stellt ihr etwas merkwürdiges fest: Er hat eine unglaublich hohe Energie und ist nicht – wie man meinen könnte – der energetisch günstigste Zustand. Würdet ihr also ein solches “Vakuum” irgendwo herstellen, wäre es nicht stabil, sondern würde ziemlich schnell in einen Zustand mit niedrigerer Energie übergehen.
Und das ist sicher nicht das, was wir uns unter einem Vakuum vorstellen – ein Vakuum sollte zumindest stabil sein und es sollte nicht mehr Energie enthalten als andere Zustände.
Deshalb ist man in der QFT auf die Idee gekommen, das Vakuum anders zu definieren: “Das Vakuum ist der Zustand mit der niedrigst-möglichen Energie.”
Kommentare (97)