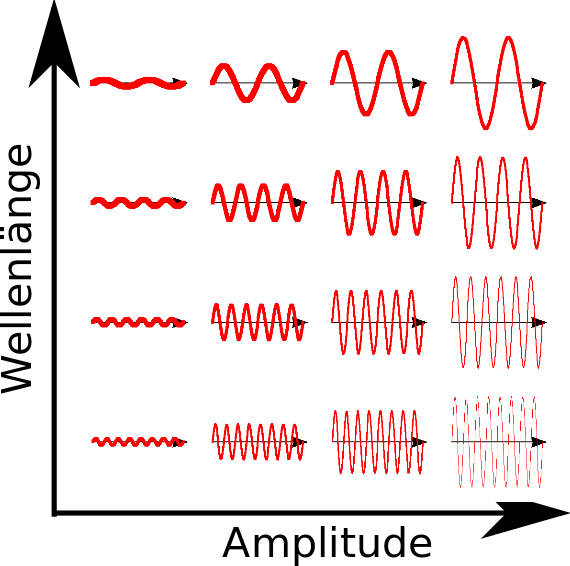
Und wie sieht dieser Vakuumzustand nun aus? Das ist zugegebenermaßen ziemlich kompliziert (und nahezu alle QFT-Bücher sagen dazu wenig bis nichts). Die genaue Erklärung findet ihr (wen wundert’s inzwischen noch…) in meiner QFT-Serie, aber zumindest eine grobe Idee will ich euch geben. Dieses Bild hier soll illustrieren, wie der Vakuumzustand aussieht. Jedes Teilbildchen gibt an, wie unser Feld aussehen könnte; die Dicke der Linie ist ein Maß für die Wahrscheinlichkeit:
Ich habe dabei die unterschiedlichen Feldkonfigurationen so sortiert, dass das ganze halbwegs übersichtlich bleibt, außerdem habe ich das Feld jetzt nur eindimensional entlang einer Linie gezeichnet, nicht wie sonst in zwei Dimensionen, einfach weil es dann etwas übersichtlicher wird: Von links nach rechts wird dabei die Amplitude (also der Wert des Feldes) immer größer, nach unten hin werden die Wellen immer kürzer. Ich habe dabei die Standard-Technik der Physik angewendet und das Feld als ebene Welle dargestellt. Ihr seht, dass große Abweichungen des Feldes vom Nullwert oder solche, die sich räumlich schnell ändern, unwahrscheinlich sind, während geringe Abweichungen vom Nullwert mit langer Wellenlänge eher wahrscheinlich sind.
Der Vakuum-Zustand eines Quantenfeldes hat folgende Eigenschaften:
Im Mittel ist alles gleich Null
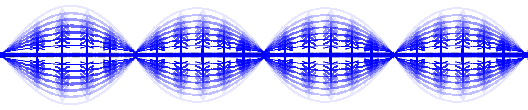
Nehmen wir als Beispiel das elektrische Feld. Wenn ich ein geladenes Teilchen in ein Vakuum bringe, dann sollte das teilchen nicht in eine Richtung gezogen werden. Die Wahrscheinlickeit, dass das elektrische Feld z.B. nach “oben” zeigt, sollte also genau so groß sein wie die, dass es nach “unten” zeigt. Das Feld hat zwar eine Wahrscheinlichkeit, von Null verschieden zu sein, aber wenn ich über alle Möglichkeiten mittele, dann sollte Null herauskommen. (In vornehmem Physiksprech heißt das “Der Erwartungswert des Feldes ist Null”.) Aus Platzgründen habe ich das im Bild oben nicht mit eingezeichnet – ihr könnt euch zu jeder der roten Kurven jeweils die dazu entgegengesetzte (die da einen berg hat, wo die gezeichnete ein Tal hat und umgekehrt) dazudenken, die hat dann genau dieselbe Wahrscheinlichkeit. Für eine bestimmte Wellenlänge kann man das auch so zeichnen (diesmal in blau, und alle unterschiedlichen Möglichkeiten zu einer Wellenlänge direkt übereinandergezeichnet):
Null ist der wahrscheinlichste Wert
Zwar gibt es eine Wahrscheinlichkeit, einen Wert des Feldes ungleich Null zu finden, doch von allen Möglichkeiten ist der Wert Null der wahrscheinlichste. (Achtung: Das heißt nicht, dass der Wert Null wahrscheinlicher ist als alle anderen Werte zusammengenommen – er ist nur wahrscheinlicher als jeder andere Wert. Wenn ich einen Würfel so fälsche, dass ich mit 20% Wahrscheinlichkeit eine 6 würfle und mit jeweils 16% jede der anderen Zahlen, dann ist 6 der Wahrscheinlichste Wert, aber in 4 von 5 Fällen werde ich trotzdem etwas anderes würfeln.) Im großen Bild seht ihr das daran, dass die Kurven mit kleinerer Amplitude dicker gezeichnet sind, in dem einfachen Bild mit einer einzigen Wellenlänge ist die dickste Linie genau die Null-Linie.
“Glatte” Felder sind wahrscheinlicher als “raue”
Anordnungen des Feldes, bei denen das Feld an benachbarten Punkten ähnliche Werte hat, sind wahrscheinlicher als solche, bei denen das Feld räumlich stark schwankt – je größer die Wellenlänge, desto wahrscheinlich ist so eine Feldkonfiguration. Weil starke räumliche Schwankungen (also kurze Wellenlängen) immer eine hohe Energie bedeuten, heißt das, dass Felder mit hoher Energie weniger wahrscheinlich sind als solche mit niedriger Energie.
Der Vakuumzustand ist raum- und zeitunabhängig
Das Vakuum sieht zu allen Zeiten und an allen Orten und auch für beliebige Beobachter immer gleich aus. Er ist zwar eine Überlagerung unterschiedlicher Möglichkeiten, aber diese Überlagerung ist zeitunabhängig. Das ist der Darstellung oben nicht ohne weiteres zu entnehmen – es sieht sogar so aus, als wäre es nicht so. Wenn ihr euch beispielsweise mit einer Rakete an einer Welle vorbeibewegt, dann schlägt die Relativitätstheorie zu und sorgt für eine Längenkontraktion, die Wellenlänge einer Welle ändert sich also. Auf den ersten Blick könnte man deshalb meinen, dass der Vakuumzustand vom Beobachter abhängen sollte, aber wenn man alles richtig ausrechnet stellt man fest, dass das nicht so ist. (Dass das Vakuum für alle immer gleich aussieht, ist in anderen Formulierungen der QFT einfacher zu sehen; ein weiterer Grund, warum die Darstellung, die ich hier wähle, selten verwendet wird.)






Kommentare (97)