Verführerisch einfach: Feynmandiagramme

Um Prozesse bei Elementarteilchen zu beschreiben, verwendet man ja gern Feynmangraphen (oder Feynmandiagramme). Vermutlich hat kein anderes mathematisches Werkzeug so sehr Einzug in die Populärwissenschaft gefunden wie diese kleinen Bildchen. Sie sind einfach, anschaulich und wurden – anders als viele andere Veranschaulichungen – nicht speziell für Laien erfunden, sondern werden tatsächlich in der Physik benutzt. Leider haben sie auch einen entscheidenden Nachteil: Man kann sie extrem leicht falsch verstehen.

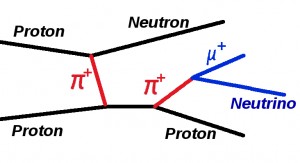
Hier erst einmal ein (extra kompliziertes) Beispiel für ein Feynmandiagramm

Die Zeitrichtung läuft hier von links nach rechts (manchmal auch von unten nach oben, da muss man aufpassen). Von links kommen also zwei Protonen, das eine sendet ein Teilchen (ein positives Pion) aus und wird dabei zu einem Neutron. Das andere Proton nimmt das Pion auf (und verandelt sich kurzfristig in ein Teilchen mit doppelter Ladung) und zerfällt dann wieder in ein Proton und ein Pion. Das Pion wiederum zerfällt in ein positiv geladenes Myon und ein Neutrino.

Eigentlich sind diese Graphen aber keine Bilder, sondern nichts als in Bilder umgeschriebene Gleichungen. (Wie man damit umgeht und so etwas prinzipiell berechnet habe ich vor seehr langer Zeit mal erklärt.) Mit diesen Gleichungen kann man berechnen, wie wahrscheinlich ein Prozess wie der oben dargestellte ist. (Generell gibt es in der Quantenwelt ja selten absolute Sicherheit, sondern nur Wahrscheinlichkeiten.)

Feynmangraphen sind ziemlich praktisch, weil sie es sehr leicht machen, sicherzustellen, dass man keine Möglichkeit für einen Prozess übersieht. Außerdem sind sie deutlich übersichtlicher als Gleichungen, weil die zweidimensionale Anordnung und das Verbinden von Punkten, an denen etwas passiert, mit Linien wesentlich einfacher zu überblicken ist als es eine einzelne Formel wäre – die für den dargestellten Prozess wäre schon ziemlich lang und unübersichtlich. (Obwohl Feynmangraphen so praktisch sind, soll der erste Vortrag von Feynman, in dem er sie vorgeführt hat, ein ziemlicher Flop gewesen sein. Man musste sich wohl erst mal an den Gedanken gewöhnen, statt Gleichungen Bildchen hinzumalen.)

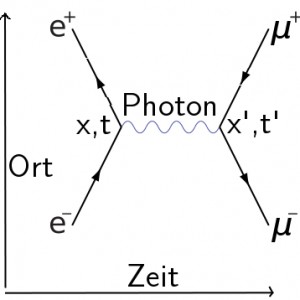
Feynmangraphen haben aber auch einen entscheidenden Nachteil: Sie verführen dazu, sie zu wörtlich zu nehmen. Nehmen wir dieses etwas einfachere Diagramm, in dem ein Elektron (e-, Pfeil in Zeitrichtung vorwärts) und ein Positron (e+, Pfeil in Zeitrichtung rückwärts) zu einem Photon werden, das dann wiederum in ein Myon und ein Anti-Myon zerfällt (das Bild stammt aus dem oben verlinkten Artikel, wo es wesentlich detaillierter erläutert wird als ich es hier tue (dezenter Hinweis…)):

Die beiden ankommenden Teilchen treffen sich am Ort x zur Zeit t – so sieht es jedenfalls aus. Aber in Wahrheit können wir den Prozess ja nicht im Detail beobachten – und schon gar nicht wissen wir, an welchem Ort sich die beiden Teilchen treffen. Wenn man bedenkt, dass es sich eigentlich um Quantenfelder handelt, nicht um Teilchen, und dass Elektron und Positron in Wahrheit eher wie zwei Wellen aussehen als wie zwei Punktteilchen, dann ergibt es gar nicht so schrecklich viel Sinn, von einem genauen Ort zu sprechen, an dem die Teilchen sich treffen. Das gleiche gilt für das eingezeichnete Photon: Scheinbar bewegt es sich vom Ort x zum Ort x’ – aber in Wahrheit ist auch das Photon eher eine Welle als ein Punktteilchen und ist über den Raum ausgebreitet.

Um den Prozess korrekt zu berechnen, muss man alle Möglichkeiten im Feynmandiagramm berücksichtigen – man muss also alle denkbaren Orte x und x’ (und auch alle möglichen Zeiten t und t’) in die Rechnung mit einbeziehen. Es wäre also zum Beispiel nicht richtig zu sagen, dass sich das Photon tatsächlich von einem bestimmten Ort zu einem bestimmten anderen bewegt, sondern es müssen alle Möglichkeiten in Betracht gezogen werden. Wir können auch nicht sagen, dass zur Zeit t”, die in der Mitte zwischen t und t’ liegt, ein Photon da ist – denn auch die Möglichkeit, dass sich die beiden Teilchen erst nach dem Zeitpunkt t” begegnet sind, müssen wir berücksichtigen.

Feynmangraphen sind also in dieser Hinsicht ziemlich irreführend.

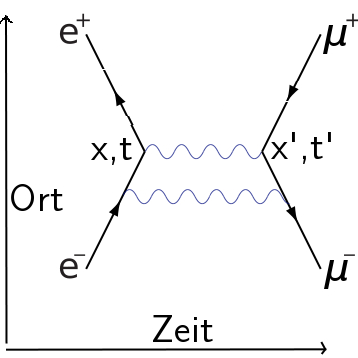
Sie sind sogar noch irreführender, wenn man bedenkt, dass es ja noch ganz andere Möglichkeiten dafür gibt, dass dieser Prozess stattfinden kann, beispielsweise diese hier

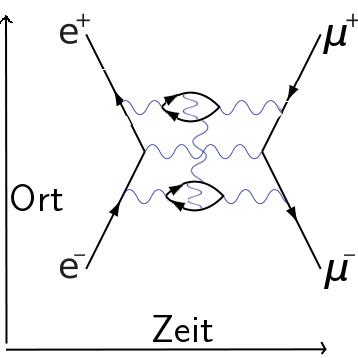
Hier wird zwischen den Teilchen noch ein weiteres Photon ausgetauscht, und auch das ist ein möglicher Prozess. Und auch dieser Prozess hier ist möglich:

Alle denkbaren Möglichkeiten, wie aus einem Elektron und einem Positron ein Myon-Anti-Myon-Paar werden kann, müssen in die Berechnung mit einbezogen werden.

Wenn ihr einen Moment nachdenkt, dann seht ihr, dass das unendlich viele Möglichkeiten sind – denn ein Elektron kann immer ein Photon aussenden, das von einem anderen geladenen Teilchen absorbiert wird. Der wahre Prozess ist also eine Überlagerung aus unendlich vielen einzelnen Feynmandiagrammen, von denen jedes einzelne wiederum eine Überlagerung unendlich vieler möglicher Orte und Zeiten für die einzelnen Knotenpunkte ist.

Dass Feynmandiagramme trotz dieser vielen Unendlichkeiten oft so nützlich sind, liegt daran, dass die elektromagnetische Wechselwirkung vergleichsweise schwach ist: Die Wahrscheinlichkeit, dass ein Elektron ein Photon aussendet, ist vergleichsweise klein. Für jeden Punkt in einem Feynmandiagramm, an dem eine Photonlinie beginnt oder endet, muss man in die Wahrscheinlichkeitsberechnung für diesen Prozess also eine kleine Zahl einbeziehen. Diagramme mit sehr sehr vielen solchen Punkten tragen deswegen zum Gesamtprozess nur sehr wenig bei. (Auf der anderen Seite werden es natürlich auch immer mehr mögliche Diagramme. Soweit ich weiß, ich nicht wirklich sauber bewiesen, dass diese unendlich vielen Diagramme tatsächlich immer weniger beitragen und vernachlässigt werden können – aber die Vorhersagen der Theorie sind so gut, dass das wohl für alle praktischen Zwecke in Ordnung geht.) Diesen Trick nennt man übrigens auch “Störungstheorie” – die komplizierteren Diagramme haben nur einen geringen Einfluss und können deshalb als kleine Störung betrachtet werden.

Feynmandiagramme funktionieren also deshalb so gut, weil wir meist nicht all zu viele von ihnen berücksichtigen müssen – und das wiederum klappt, weil die elektromagnetische Wechselwirkung einigermaßen schwach ist. Bei der starken Kernkraft, die die Quarks in den Protonen zusammenhält, ist das anders: Hier ist die Wechselwirkung so stark, dass in den meisten Fällen auch die feynmandiagramme mit vielen Knotenpunkten nicht vernachlässigt werden dürfen. Deswegen werden in dieser Theorie oft keine Feynmandiagramme berechnet, sondern andere Wege beschritten; beispielsweise die Simulation der Quantenfelder selbst. Einige Effekte der QFT lassen sich auch gar nicht mit Hilfe von Feynmandiagrammen beschreiben, ein (ziemlich kompliziertes) Beispiel findet ihr hier.

Virtuelle Teilchen

Aber es kommt noch etwas komplizierter. Betrachten wir nochmal das Beispiel oben, bei dem sich Elektron und Positron vernichten und – zwischendurch – ein Photon herauskommt. Dieses Photon hat – wegen der Erhaltungssätze – genau die Energie und den Impuls der ankommenden beiden Teilchen. Nehmen wir als Beispiel an, dass unsere beiden einlaufenden Teilchen frontal zusammenstoßen. Dann ist ihr Gesamtimpuls Null, das Photon hat also auch keinen Impuls, sondern nur Energie. Für Energie und Impuls eines “echten” Photons gilt aber die einfache Beziehung p=E/c (Impuls gleich Energie durch Lichtgeschwindigkeit). Beide Beziehungen lassen sich nicht gleichzeitig erfüllen.

Unser Photon im Inneren des Feynmangraphen ist ein virtuelles Photon – eins, das nicht die richtige Beziehung zwischen Energie und Impuls hat. Generell sind alle Teilchen, die auf den inneren Linien eines Feynmandiagramms auftauchen, solche “virtuellen” Teilchen. (Für ein virtuelles Teilchen mit Masse gilt dann die Gleichung für die kinetische Energie – in der klassischen Physik E=(1/2) m v² – nicht.)  Aus Gründen, die ich jetzt hier nicht erkläre, bezeichnet man solche Teilchen als Teilchen, die “nicht auf der Massenschale liegen” (man sagt auch kurz, sie sind “off-shell”).

Virtuelle Teilchen verletzen also die korrekte Beziehung zwischen Energie und Impuls. Sie verletzen aber nicht die Energie- und Impulserhaltung – im Gegenteil: Sie sind ja gerade deshalb “off-shell”, damit sie die Erhaltungssätze korrekt erfüllen können. Die Energie ist auch bei virtuellen Teilchen erhalten.

Virtuelle Teilchen, die sehr stark “off-shell” sind, sind allerdings vergleichsweise unwahrscheinlich. Je größer die Strecke ist, die so ein Teilchen zurücklegen soll, desto unwahrscheinlicher wird der Prozess. (Wer eifrig meine QFT-Serie gelesen hat, erkennt jetzt einen guten alten Bekannten wieder: den Propagator.) Prozesse, bei denen die virtuellen Teilchen große Energien mit sich herumtragen, können deshalb nur auf sehr kleinem Raum stattfinden und die virtuellen Teilchen können entsprechend nur eine kurze Zeit existieren. Das ist vermutlich auch der Grund, warum man dieses Phänomen leicht mit der Unschärferelation verwechselt, nach der die Energieunschärfe und die Zeitunschärfe ja zusammenhängen. (Gerade die Energie-Zeit-Unschärfe ist aber eine ziemlich knifflige Unschärferelation – und bevor jemand fragt: Ja ich setze es mal auf die Themenliste…)

Also: Virtuelle Teilchen verletzen nicht die Energieerhaltung, sondern liegen nicht auf der Massenschale (sie verletzen die für diese Teilchensorte gültige Energie-Impuls-Beziehung).

Feynmandiagramme und das Vakuum

Eigentlich beschäftige ich mich im Moment ja vor allem mit Nichts – oder genauer gesagt, dem Vakuumzustand. Für die Überlegungen zum Vakuum ist die Überlegung hier deswegen wichtig, weil ja oft argumentiert wird, im Vakuum würden sich ständig virtuelle Teilchen-Antiteilchen-Paare bilden. Ein zugehöriges Feynmandiagramm dazu könnte so aussehen:

Hier entstehen aus dem Nichts ein Elektron, ein Positron und ein Photon und vernichten sich am Ende wieder. Alle drei fliegen von ihrem Entstehungsort zu ihrem Vernichtungspunkt – dass man die drei Linien nicht übereinander zeichnet sondern zwei von ihnen krümmt, hat überhaupt keine Bedeutung. Und wie auch sonst muss man hier alle Möglichkeiten in Betracht ziehen, wie der Prozess passieren kann. Es ist also nicht richtig, sich vorzustellen, dass an einem bestimmten Punkt im Raum zu einer bestimmten Zeit gerade für einen Moment ein Elektron sitzt, wie es oft in anschaulichen Erklärungen gemacht wird. Denn genauso trägt zum Endergebnis der Prozess bei, wo genau an dieser Stelle ein Positron sitzt – oder auch gar kein Teilchen. Wenn man das Vakuum mit Hilfe von Feynmandiagrammen beschreiben will, dann muss man alle Möglichkeiten überlagern.

Zu sagen, dass sich im Vakuum ständig Teilchen und Antiteilchen bilden ist also auch in dieser Hinsicht etwas irreführend. (Hinzu kommt, dass die Überlagerung, von der wir hier sprechen, eine quantenmechanische Überlagerung ist – es werden nicht einfach Wahrscheinlichkeiten addiert, sondern Wahrscheinlichkeitsamplituden. Das habe ich auch im oben verlinkten Artikel über Feynmandiagramme, aber auch hier erklärt.)

Da bei Feynmandiagrammen die Energie immer erhalten ist und in unserem Diagramm Teilchen aus dem Nichts entstehen, muss eins der Teilchen im Diagramm – rein rechnerisch – eine negative Energie tragen. Das ist nicht problematisch, weil es sich ja nur um ein “virtuelles” Teilchen handelt, aber es zeigt noch einmal, dass sich hier eben keine Energie aus dem Vakuum “geborgt” wird – diese Vorstellung ist einfach falsch.

Mehr zum Vakuum gibt es dann demnächst – da kommen dann auch wieder Feynmangraphen vor, deswegen lohnte es sich, hier ein paar Missverständnisse auszuräumen.

Feynmangraphen sind also wirklich eine tolle und praktische Sache – aber ganz so einfach, wie man oft denkt, sind sie nicht zu interpretieren.