Das Vakuum ist schon eine ziemlich komplizierte Sache. Dass es nicht einfach “Nichts” ist, dazu habe ich inzwischen ja einiges geschrieben. Heute schaue ich auf einen anderen Aspekt des Vakuums, die viel zitierte Vakuumpolarisation, die oft als Beleg dafür angeführt wird, dass sich im Vakuum ständig Teilchen und Antiteilchen bilden. Aber wieder einmal ist die Sache komplizierter, als man denkt…
Die Geschichte der Vakuumpolarisation
Die Idee, dass das Vakuum eine “Struktur” hat, ist natürlich insofern alt, als man ja früher an den Äther geglaubt, hat, das Medium, in dem sich elektromagnetische Wellen ausbreiten. (Weil man sich nicht vorstellen konnte, dass es Felder geben kann, die nicht an Materie geknüpft sind.) Doch Anfang des 20. Jahrhunderts hat Einstein ja mit dieser Vorstellung aufgeräumt und das Vakuum konnte wieder einfach Nichts sein.
Jedenfalls bis 1928. Da hat der berühmte Physiker Dirac seine ebenso berühmte Dirac-Gleichung aufgestellt, die das Verhalten von Elektronen beschreibt. Die Gleichung sagte viele Dinge richtig vorher (beispielsweise den Spin der Elektronen, also die Tatsache, dass sie sich ein bisschen wie kleine Kreisel benehmen). Es gab aber auch einen beunruhigenden Aspekt: Laut der Diracgleichung müsste ein Elektron Zustände mit negativer Energie annehmen können. Da wir aber nicht beobachten, dass Elektronen immer mehr und mehr Energie verlieren und ihre Energie dabei gegen negativ unendlich geht, war da wohl etwas faul.
Dirac hatte genügend Selbstbewusstsein, um seine Gleichung nicht einfach wegzuwerfen (dazu fand er sie zu schön), sondern um sie zu retten. Dazu postulierte er, dass es die negativen Zustände zwar gibt (denn die Gleichung sagte sie ja vorher), dass sie aber schon alle von Elektronen besetzt seien. (Ein fundamentales Gesetz, das Pauli-Prinzip, sagt, dass niemals zwei Elektronen im gleichen Zustand sein können.) Das ist ähnlich wie im Uni-Hörsaal – ihr könnt euch nicht einfach auf den besten Platz setzen, wenn ihr reinkommt, sondern nur auf den besten noch freien Platz. Dirac postulierte ein Meer von Elektronen, die all die negativen Zustände besetzen – “Dirac sea” (zu deutsch leider mit “Dirac-See” statt “Dirac-Meer” übersetzt) genannt.
Er kam zusätzlich auf die Idee, dass man mit genügend Energie ein Elektron aus so einem negativen Energiezustand herausschlagen können sollte – was dann übrig bleibt ist ein “Loch”, ein fehlendes Elektron. Und das würde sich wie ein teilchen mit positiver Ladung verhalten – das Positron war entdeckt. (Ja, diese Geschichte habe ich schon mal erzählt, aber mir geht es um den Aspekt, der jetzt kommt.) Dieses Bild hier soll das veranschaulichen: Unten in blau die besetzten Zustände mit negativer Energie, von denen Elektronen in Zustände mit positiver Energie (gelb) gehoben werden und ein Loch zurücklassen.
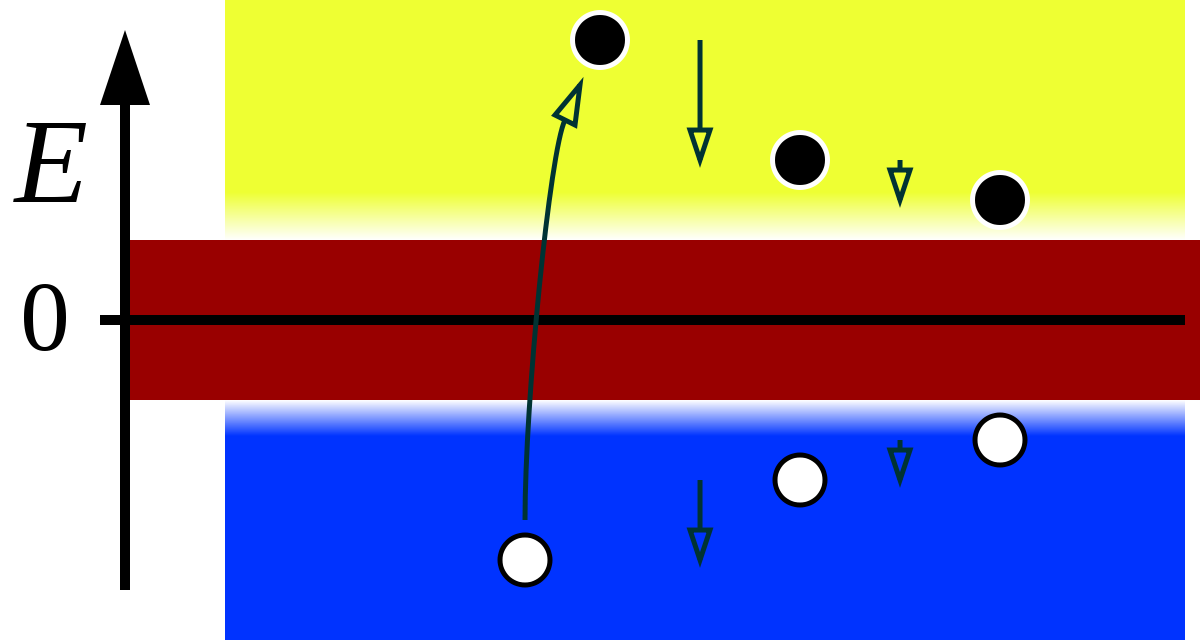
By Incnis Mrsi – Own work, Public Domain, Link
Laut Dirac war das Vakuum also angefüllt mit lauter Elektronen in Zuständen mit negativer Energie – dass wir davon nichts merken, liegt eben daran, dass die überall sind und sozusagen zum Vakuum “dazugehören”.
Aber stimmt das auch? Oder würde man nicht doch etwas merken?
1934 veröffentlichte der Physiker Rudolf Peierls einen Artikel mit dem Titel “The vacuum in Dirac’s Theory of the Positive Electron” (Das Vakuum in Diracs Theorie des positiven Elektrons). Darin verfolgte er die Idee, die Dirac-See zu stören. Wenn man beispielsweise eine elektrische Ladung im Vakuum betrachtet, müsste deren Feld dann nicht die vielen Elektronen in ihren Zuständen beeinflussen? Die umgebenden Elektronen würden sich ein wenig umordnen (sie würden von einer positiven Ladung etwas angezogen, von einer negativen abgestoßen) und würden dadurch das elektrische Feld der Ladung ein wenig abschwächen.
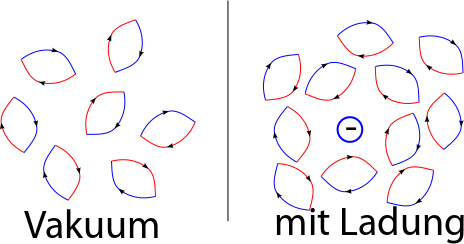
Etwas ähnliches kennt man von normalen Materialien: Bringt man zum Beispiel einen Salzkristall in ein elektrisches Feld, dann verschieben sich die elektrisch geladenen Ionen innerhalb des Kristalls ein wenig und schwächen so das Feld im Inneren des Kristalls ab. Das kann man sich etwa so vorstellen (links unverschobene, rechts verschobene Ionen):
(Dieses wunderschöne Bild habe ich für mein demnächst erscheinendes Buch erstellt – was auch erklärt, warum ich im Moment wenig blogge…)
Dieses Phänomen bezeichnet man als “elektrische Polarisation” und Materialien, die so reagieren, nennt man “dielektrisch” (das liest man “di-elektrisch”, griechisch “dia” heißt “hindurch”, wen ich mich an meine Griechisch-Stunden richtig erinnere). Man kann Materialien also polarisieren und dabei wird das elektrische Feld in ihrem Innere schwächer.
Peierls erkannte, dass nach Diracs Theorie dasselbe auch mit dem vakuum möglich sein müsste. Wenn wir eine elektrische Ladung, beispielsweise die eines Elektrons, messen, dann messen wir gar nicht wirklich den richtigen Wert der Ladung, sondern wir messen einen Wert, der zu klein ist,weil die Ladung durch die verschobenen Elektronen etwas abgeschwächt wird. Das Vakuum kann also polarisiert werden – der Begriff der “Vakuumpolarisation” war geboren.
Hinweis: Ich bin mir nicht sicher, ob es wirklich Peierls war, der als erster diese Idee hatte. Sein paper ist jedenfalls das älteste, das ich bei google scholar zum Thema “vacuum polarisation” finden konnte — aber ich habe nicht wirklich sehr ernsthaft recherchiert.
Tja, und dann kam es wie so oft in der Physik: Die Idee der Dirac-See wurde Ende der 40er Jahre als unnötig erkannt, als man die Quantenfeldtheorie entwicelte und sah, dass die Lösungen mit negativer Energie ganz sauber als Anti-Teilchenlösungen mit positiver Energie aufgefasst werden können. In der modernen QFT braucht man keine Dirac-See mehr. Aber der Begriff “Vakuumpolarisation” blieb – er wird sogar heute noch verwendet. Nur seine Bedeutung hat sich leicht verschoben.
Die Vakuumpolarisation in der QFT
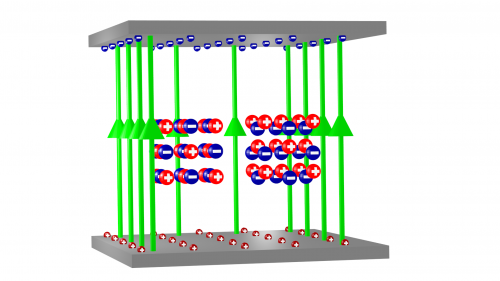
In der QFT wird die Vakuumpolarisation oft mit Hilfe der berühmten ständig aus dem Nichts entstehenden und wieder vergehenden Teilchen-Antiteilchen-Paaren erklärt. Die Idee dahinter ist die folgende: Nehmt an, dass es tatsächlich so wäre, dass im Vakuum ständig Elektronen und Positronen aus dem Nichts entstehen. Im Mittel werden wir davon – ähnlich wie bei der Dirac-See – nicht viel merken, weil an jedem Punkt immer gleich viele Elektronen und Positronen in diesen sogenannten “virtuellen” Paaren sind. Wenn wir jetzt aber eine elektrische Ladung in unser Vakuum bringen, dann können sie diese Teilchen-Antiteilchen-Schleifen passend zu dieser Ladung ausrichten, etwa so:
(Die Farben sollen hier die Ladung kennzeichnen – negativ ist blau, positiv ist rot. Habe ich aber nicht bei allen Bildern hier konsequent so gemacht…)
Und damit wird dann die Ladung – genau wie in unserem dielektrischen Kristall oben – ein wenig abgeschirmt. Dieses Phänomen könnte man mit Recht als Vakuumpolarisation bezeichnen.
Dass ein solches Phänomen tatsächlich existiert, dass sich also die messbare Größe einer elektrischen Ladung ändert, wenn man der Ladung näherkommt, daran besteht eigentlich kein Zweifel – ein Experiment, dass das belegt, ist eine winzige Verschiebung der Energien im Wasserstoff-Atom, die Lamb-Shift (dazu schreibe ich bei Gelegenheit mehr – jaja, eine Endlosserie über gar nichts, das hatte auch noch keiner…).
Also gibt es die Vakuum-Polarisation wirklich, oder?
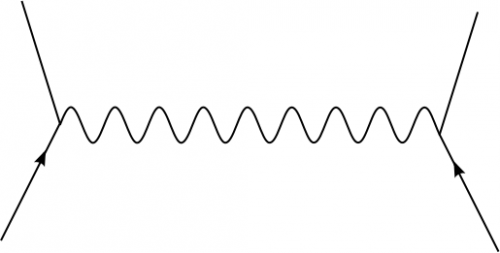
Auch das ist aber wieder nicht so einfach, wie es scheint. Betrachten wir noch einmal unser Teilchen, das von den Vakuumpolarisationen umgeben ist. Um seine Ladung zu messen, muss es mit einem anderen Teilchen in seiner Nähe wechselwirken. In der Sprache der QFT kann ich diese Wechselwirkung mit Hilfe von Feynman-Diagrammen beschreiben. Dabei tauschen die beiden Teilchen ein (virtuelles) Photon aus. Das sieht etwa so aus (Achtung: die Zeitrichtung läuft diesmal von unten nach oben im Bild):
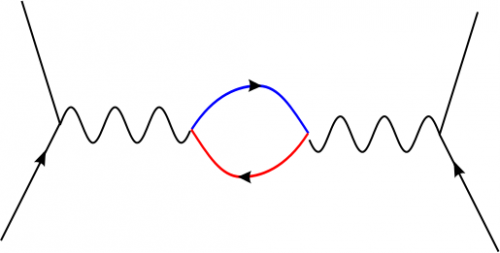
Hier ist jetzt von der Vakuumpolarisation nichts zu merken – das Photon wird direkt ausgetauscht. Aber die “Teilchen des Vakuums” könnten ja mit dem Photon wechselwirken – sie könnten es zum Beispiel erst absorbieren und dann wieder emittieren. Das würde dann so aussehen:
Tja, und schon haben wir den Ärger: Ist das nun eine Teilchen-Antiteilchen-Schleife im Vakuum, die ein Photon absorbiert und dann wieder aussendet? Oder ist es in Wahrheit ein Photon, das einfach durchs Vakuum fliegt, sich zwischenzeitig in ein Teilchen-Antiteilchen-Paar aufspaltet und dann wieder zu einem Photon wird? Dann hat das Vakuum nicht so viel mit der Sache zu tun. Man könnte versucht sein zu argumentieren, dass im Bild ja die Schleife “unten” anfängt, also bevor sie das Photon absorbiert – aber das ist wieder der Ärger mit der zu wörtlichen Interpretation der Feynman-Diagramme. Denn die beiden Linien (die rote und die blaue) stellen symbolisch einfach nur dar, dass die beiden Teilchen vom linken zum rechten Knoten-Punkt in der Raumzeit fliegen – dass man sie sie gekrümmt zeichnet, ist nur, damit man noch was erkennt. Rechnerisch muss man bei der Berechnung dieses Diagramms einfach die beiden virtuellen Teilchen vom einen Knoten zum anderen laufen lassen.
Und ganz ähnlich wie letztes Mal beim Casimir-Effekt führen beide Betrachtungsweisen zum richtigen Ergebnis. Die zweite ist typischerweise die, die man verwendet, um so ein Feynmandiagramm zu berechnen, und die hat eigentlich nicht mehr wirklich etwas mit “Vakuumpolarisation” zu tun, denn wir haben ja am Anfang nicht einfach Nichts, sondern ein ankommendes Photon. Trotzdem werden Feynmandiagramme dieser Art oft als “Vakuumpolarisation” bezeichnet. Ein Beleg dafür, dass sich im Vakuum ständig Teilchen-Antiteilchen-Paare bilden, sind sie aber nicht, denn man kann sie eben auch anders interpretieren.
Und das ist vielleicht ein generelles Problem bei all diesen Ideen zum Vakuum: Wann immer wir die Vakuum-Effekte messen wollen, müssen wir das Vakuum mit irgendwelchen Teilchen stören – und dann ist es eben kein Vakuum mehr. In der Sprache der Feynmandiagramme betrachtet braucht man immer (mindestens) ein Teilchen, das in die betrachtete Region hineinfliegt und eins, das wieder herauskommt, und ob ich die dort stattfindende Reaktion dem Teilchen oder dem Vakuum zuschlage, ist ein eher eine Frage des Geschmacks als der Physik.
Eine Sache ist aber auf jeden Fall klar: Auch wenn Ihr die Schleife im Diagramm oben als Schleife im Vakuum interpretieren wollt, die mit einem Photon wechselwirkt – eine Eigenschaft hat sie mit Sicherheit nicht: Sie “borgt” sich keine Energie aus dem Vakuum mit Hilfe der Unschärferelation. Denn in einem Feynmandiagramm gelten strenge Regeln: An jedem Punkt des Feynmandiagramms sind Energie und Impuls exakt erhalten – die Energie des Teilchen-Antiteilchen-Paares in der Mitte ist exakt so groß wie die des einlaufenden (und die des auslaufenden) Photons. (Falls die Energie des Photons sehr klein ist, heißt das, dass eins der beiden Teilchen in der Schleife eine negative Energie haben muss – das scheint zwar unsinnig, ist aber notwendig, damit alles richtig herauskommt. Anders als die Lösungen mit negativer Energie bei Dirac macht diese negative Energie hier aber weniger Ärger, weil sie nur bei virtuellen Teilchen auftreten darf.)
Also: Auch die Vakuumpolarisation liefert keinen echten Beweis dafür, dass im Vakuum Teilchen-Antiteilchen-Paare aus dem Nichts entstehen. Wenn man sie so auffassen will, dann ist auf jeden Fall die Energie erhalten – der Kram mit der Unschärferelation hält einer genaueren Betrachtung nicht stand.
Kleiner Hinweis: Nächste Woche wird es hier noch stiller sein als sonst – ich bin zur Konferenz in Barcelona (angesichts von U-Bahnschächten mit ca. 35° und U-Bahnen mit Klimatisierung auf 18° ist die Erkältung vermutlich wieder vorprogrammiert…).






Kommentare (106)