Die Physik ist ja voller abgefahrener und faszinierender Phänomene – Vakuumfluktuationen, negative Temperaturen, Quantenverschränkungen und und und. Aber heute schauen wir uns mal etwas ganz simples und einfaches an – ungefähr das einfachste physikalische Phänomen, das man sich vorstellen kann: Ein Teilchen fliegt von A nach B. (Danke an die Kommentatoren Loqi und Rainer Zufall, die mich mit klugen Fragen auf die Idee brachten, diesen Artikel zu schreiben.)
Um die Sache konkreter zu machen, stellen wir uns vor, dass vor uns auf dem Tisch zwei Detektoren stehen, mit denen man Elektronen messen kann. Die beiden Detektoren haben einen Abstand von einem Meter und können ein Elektron sehr genau lokalisieren (wir können uns zum Beispiel vorstellen, dass sie eine sehr kleine Kammer enthalten, in der die Lagun des Elektrons gemessen wird, oder eine Art Geigerzähler, oder sonst irgendetwas. Da es hier wirklich nur um die fundamentalen Grundlagen geht, lasse ich das einfach offen.) Wir ignorieren alle äußeren Einflüsse, über dem Tisch herrscht also Vakuum und der Tisch wiegt auch nichts und zieht deswegen das Elektron nicht an oder sonst etwas. Wir haben also wirklich nur ein Elektron zwischen zwei Punkten A und B.
Genau um 12:00:00Uhr messen wir das Elektron im Detektor A und um 12:00:01Uhr im Detektor B, einen Meter entfernt. Das Elektron (oder allgemein das Teilchen) hat sich also von A nach B bewegt. Wie beschreibt man diesen unglaublich simplen Sachverhalt in den unterschiedlichen physikalischen Theorien und was hat das Elektron laut diesen Theorien zwischendurch gemacht?
Klassische Physik
Fangen wir erst mal mit der klassischen Physik an, die ihr vermutlich mal in der Schule gelernt habt und laaaangweilig fandet.
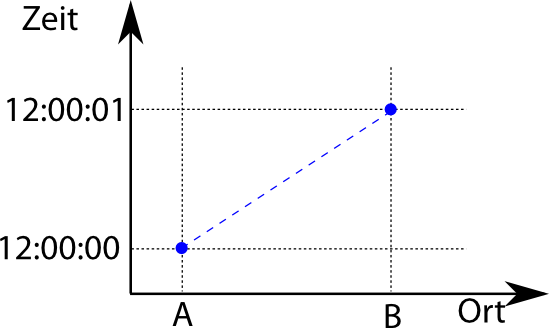
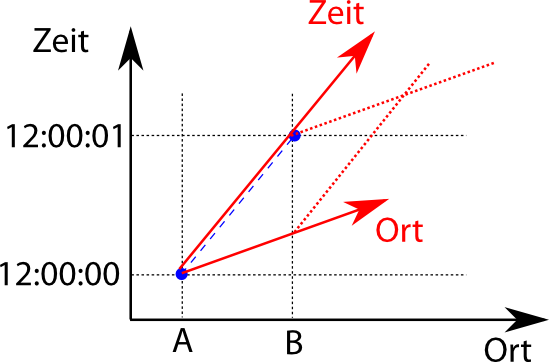
Nach den Regeln der klassischen Physik (die newtonschen Axiome) bewegt sich ein Elektron, auf das keine Kräfte wirken, mit konstanter Geschwindigkeit. Wenn es also um 12:00:00Uhr bei A war und um 12.00:01Uhr bei B in einem Meter Entfernung, dann hat es in einer Sekunde eine Strecke von einem Meter zurückgelegt und sich somit mit einer Geschwindigkeit von 1m/s bewegt. Entsprechend kann ich ausrechnen, wo das Elektron zwischendurch war und kann es z.B. in ein Diagramm einzeichnen:
Ort und Geschwindigkeit unseres Elektrons sind also zu jedem Zeitpunkt festgelegt.
Wenn ihr Lust habt, könnt ihr die Formeln nehmen, die man in allen Physik-Schulbüchern findet, und zum Beispiel die kinetische Energie (also die Bewegungsenergie) des Elektrons ausrechnen. Dafür gilt die Formel E=(1/2) m v². (Da die Masse des Elektrons sehr klein ist, ist seine Energie in diesem Fall extrem winzig, etwa 0,00000000000000000000000000000045 Joule, wenn ich mich bei den Nullen nicht verzählt habe…)
Mehr gibt es in der klassischen Physik dazu nicht zu sagen.
Oder doch?
Bezugssysteme
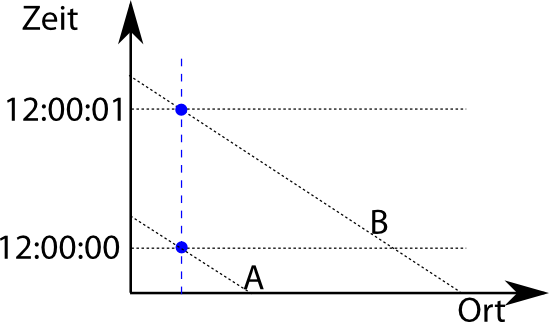
Stellt euch eine zweite Beobachterin vor, die sich mit einem Meter pro Sekunde in dieselbe Richtung bewegt wie das Elektron. Für sie stellt sich das Experiment anders dar: Das Elektron steht still und der Tisch mit den beiden Detektoren ist es, der sich bewegt. Ihr Diagramm, das beschreibt, was das Elektron tut, sieht entsprechend anders aus:
Wenn sich das Elektron im Tisch-System von links nach rechts bewegt, dann bewegen sich die Detektoren A und B im System der Beobachterin von rechts nach links, ihre Linien sind also andersherum geneigt.
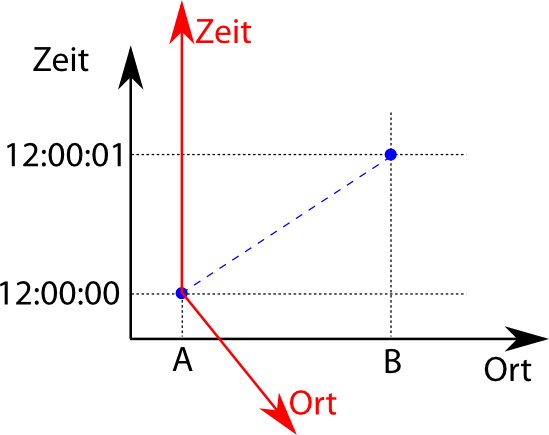
Ihr könnt auch, das, was die Beobachterin sieht, in euer Diagramm mit einzeichnen, das sähe dann etwa so aus (wobei die Regel hier so ist, dass Linien für konstante Orte senkrecht auf der roten Orts-Linie stehen; unten, wenn es um die Relativitätstheorie geht, sieht das etwas anders aus)::
Die Zeitachse ist euch und die mitbewegte Beobachterin dieselbe, aber die Ortsachse liegt für sie anders. (Damit keine Missverständnisse aufkommen – euer System ist nicht dadurch ausgezeichnet, dass Ort und Zeit genau senkrecht stehen – wenn die mitbewegte Beobachterin die Grafik zeichnet, dann sind es ihre Achsen, die senkrecht aufeinander stehen und eure, die verzerrt sind.)
Interessanterweise hat für sie das Elektron auch keine kinetische Energie. Der Energiegehalt eines Systems hängt also von der Beobachterin ab.
Das ist ein Punkt, der in Büchern zur klassischen Physik oft nicht gewürdigt wird: Wie viel Energie in einem System steckt, hängt davon ab, wie ihr euch relativ zum System bewegt. Das gilt auch für das Universum als ganzes – es gilt zwar für jede Beobachterin Energieerhaltung, aber wie groß die Gesamtenergie ist, darüber herrscht keine Einigkeit. Das ist die so genannte Galilei-Invarianz. (Sehr schön erklärt im Buch von Penrose “Road to Reality”.)
Das man Raumpunkte nicht irgendwie kennzeichnen kann (außer durch Objekte, die man dort platziert), kann man nicht entscheiden, wer recht hat. Ist der Tisch mit den Detektoren fest im Raum verankert oder ist es das Elektron, während der Tisch sich durch den Raum bewegt? Das kann man schlicht und einfach nicht sagen.
Newton selbst hat das so übrigens nicht so akzeptiert – er glaubte an einen absoluten Raum, obwohl seine Bewegungsgesetze keine Möglichkeit bieten, diesen absoluten Raum festzulegen. Kant hat das dann entsprechend übernommen, als er seine Kritik der reinen Vernunft schrieb, und den absoluten Raum sogar zu einer Denknotwendigkeit erklärt.
Newton hatte auch einen guten Grund, das so zu glauben – einige Bewegungen lassen sich nämlich “absolut” messen. Immer wenn sich etwas dreht, dann wirken Fliehkräfte, und diese Kräfte könnt ihr nicht einfach dadurch zum Verschwinden bringen, dass ihr euch passend mitbewegt. Zum Glück muss ich das nicht ausführlich erklären, denn das hat Florian schon mal gemacht, und zwar in dieser Buchrezension hier. Mich würde das aber etwas vom eigentlich Ziel dieses Artikels abbringen, denn es soll hier ja nicht so sehr darum gehen, was Raum und Zeit sind (obwohl ich dazu gleich noch ein bisschen was sagen werde), sondern darum, was unser Elektron tut.
Also: Im Ruhesystem unseres Tisches bewegt sich das Elektron mit einer konstanten Geschwindigkeit von A nach B und hat dabei eine kinetische Energie. Für eine andere Beobachterin stellt sich die Sache anders dar, das Elektron ruht und hat entsprechend auch keine kinetische Energie.
So, das ist jetzt aber wirklich alles, was es darüber in der klassischen Physik zu sagen gibt. Oder?
Oder auch nicht.
Das Lagrange-Prinzip
Man kann die Bewegung des Elektrons auch noch auf ganz andere Weise beschreiben. Innerhalb der klassischen Physik ist diese Beschreibung nur eine mathematisch elegante Umformulierung, die keine neuen physikalischen Erkenntnisse bringt, aber wenn wir später zur Quantenmechanik übergehen, wird sie uns sehr nützlich sein.
Diese Beschreibung ist das sogenannte Lagrange-Prinzip oder auch Prinzip der kleinsten Wirkung. Es funktioniert so:
Wir wissen nicht, was das Elektron auf seinem Weg von A nach B gemacht hat, wir wissen nur, dass es zu einer Zeit bei A und zu einer anderen Zeit bei B war. Welchen der möglichen Wege hat es genommen?
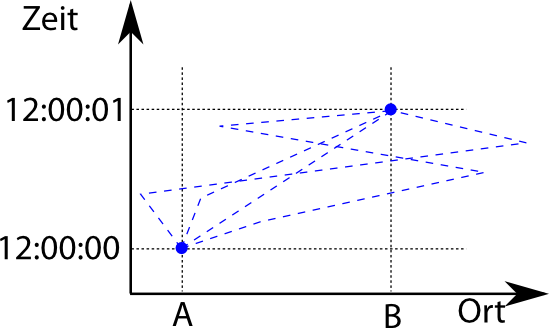
Dazu betrachtet man alle denkbaren Wege, die das Elektron hätte nehmen können: Den direkten Weg, einen Weg, wo es dreimal zwischen A und B hin- und herflitzt, einen, bei dem es das erste Stück ganz gemächlich dahinkriecht und dann plötzlich beschleunigt, um gerade noch rechtzeitig anzukommen, einen, bei dem es erstmal zum Jupiter fliegt (überlichtschnell, aber das macht nix, noch sind wir in der ganz klassischen Physik) und so weiter. Dabei ist wichtig, dass zwei “Wege” auch dann unterschiedlich sind, wen das Teilchen genau dieselbe Strecke zurücklegt, nur auf unterschiedliche Weise. Es ist also ein anderer Weg, wenn das Elektron erst 10 Zentimeter mit einer Geschwindigkeit von 0,2m/s zurücklegt und dann nach einer halben Sekunde plötzlich schneller wird, um nach einer Sekunde anzukommen. Hier sind ein paar der Wege in unser Diagramm eingezeichnet (alle unendlich vielen Möglichkeiten einzuzeichnen ist etwas unübersichtlich):
Wir betrachten also alle denkbaren Möglichkeiten in unsere Diagramm, wie das Elektron in der richtigen Zeit von A nach B kommen kann. (Anmerkung für die Physik-Nerds: Vermutlich müssen die Pfade eigentlich stetig differenzierbar sein und dürfen keine scharfen Knicks aufweisen; ganz sicher bin ich mir da allerdings nicht. Da das aber für das prinzipielle Verständnis egal ist, kümmere ich mich um solche Details hier nicht.)
Für jeden dieser Wege berechnen wir jetzt eine spezielle Größe, die Wirkung genannt wird. (Dieser Begriff ist sehr unglücklich gewählt, denn mit dem, was man im Alltag als “Wirkung” bezeichnet, hat diese Wirkung so ziemlich nichts zu tun.) Dazu messen wir zu jedem Zeitpunkt die kinetische Energie des Elektrons und addieren all diese Werte auf (mathematisch korrekt muss man über die Zeit integrieren). Derjenige Weg, bei dem die Wirkung am kleinsten ist, ist der, den das Elektron tatsächlich nimmt. (Wenn auf das Elektron noch Kräfte wirken, dann muss man die ebenfalls in der Wirkung berücksichtigen, aber das tun wir nicht.)
Dass das wirklich der Weg ist, bei dem das Elektron mit konstanter Geschwindigkeit auf geradem Weg fliegt, kann man leicht einsehen: Jeder Umweg bedeutet, dass das Elektron seine mittlere Geschwindigkeit erhöhen muss, also erhöht sich auch die mittlere Energie und damit die Wirkung. Das Elektron muss also den geraden Weg nehmen. Und von allen Möglichkeiten, den geraden Weg zu nehmen, ist die Wirkung dann am kleinsten, wenn die Geschwindigkeit konstant ist – denn ein Stück mit langsamer Geschwindigkeit muss ja mit einem mit hoher Geschwindigkeit kompensiert werden. Da in die kinetische Energie aber das Quadrat der Geschwindigkeit eingeht, ist das immer ungünstiger als die konstante Geschwindigkeit.
Ihr könnt euch das Leben auch – mit Hilfe der Beobachterin von vorhin – noch einfacher machen: Im Bezugssystem des Elektrons ist der Weg mit der kleinsten Energie logischerweise der, wo das Elektron brav auf der Stelle sitzt und darauf wartet, dass Detektor B vorbeikommt, da ist die Wirkung gleich Null. Wenn das in diesem System so gilt, dann muss es auch im Tisch-System gelten, also muss das Elektron mit konstanter Geschwindigkeit fliegen.
So, damit ist nun aber wirklich im Rahmen der klassischen Physik alles gesagt, was es zu sagen gibt.
Relativitätstheorie
Verlassen wir die “ganz” klassische Physik und schauen wir, wie sich das Bild ändert, wenn wir zur Relativitätstheorie übergehen. (Ich mache hier keinen Unterschied zwischen spezieller und allgemeiner RT, weil hier keine Schwerefelder wirken und deswegen beide Theorien dasselbe sagen – mehr zur Allgemeinen RT findet ihr, wenn ihr rechts bei “Artikelserien” klickt, da gibt es eine Serie zur Raumzeitkrümmung.) Warnhinweis: Falls hier jemand der üblichen Verdächtigen in den Kommentaren etwas über “Deppenphysik” und “Warum die RT Quatsch ist” schreiben will – ich werde solche Kommentare vermutlich schlicht löschen, weil ich keine Lust auf immer den gleichen Blödsinn habe.
Ich habe die RT hier übrigens generell etwas kurz abgehandelt, weil sie für die folgenden Betrachtungen zur Quantenphysik nicht ganz so wichtig ist.
In der Relativitätstheorie passiert etwas Ähnliches wie oben, als wir unsere Sicht der Dinge mit der der mitbewegten Beobachterin verglichen haben. Dort war es ja so, das wir uns zwar einige darüber waren, zu welchem Zeitpunkt das Elektron bei A und B war, aber nicht, was die relativen Positionen waren.
In der Relativitätstheorie ändert sich jetzt auch die Zeitwahrnehmung – die mitbewegte Beobachterin hat eine etwas andere Zeitwahrnehmung als wir, das ist die berühmte Zeitdilatation. Im Raumzeit-Diagramm verkippt sich dabei auch die Zeitachse, wobei die folgende Darstellung nur schematisch zu verstehen ist, sie ist quantitativ absolut falsch, denn bei Geschwindigkeiten von 1m/s ist der Unterschied im Zeitablauf extrem winzig (Sorry, hier war erst ein falsches Bild, ich hoffe, diese Version stimmt jetzt einigermaßen):
Etwas mehr über die Regeln, die gelten, wenn man zwischen unterschiedlichen Beobachterinnen hin- und hertransformiert, habe ich vor langer Zeit mal beim kleinen Sommerrätsel geschrieben. Da das für das folgende nicht so wichtig ist, gehe ich hier nicht näher darauf ein.
Ein Punkt ist hier aber wichtig: Da man sich innerhalb der Relativitätstheorie nicht einig ist, wie der Zeitablauf zwischen den beiden Messungen genau war, ist es sinnvoll, sich immer auf konkrete Ereignisse zu beziehen. Man spricht also vom Ereignis A, wenn das Elektron im Detektor A gemessen wird und vom Ereignis B, wenn es bei B gemessen wird. Dass es beide Ereignisse gibt und dass B nach A stattfindet, darüber sind sich alle einig – aber jede Beobachterin hat ihre eigene Vorstellung davon, wie viel Zeit zwischen A und B vergangen ist und wie weit die beiden Ereignisse im Raum auseinanderliegen. Wenn ich im folgenden von A und B rede, meine ich deswegen meist nicht mehr die Detektoren, sondern das jeweilige Messereignis.
Eigenzeit
Sind wir damit mit der Relativitätstheorie durch? Nicht ganz. Denn die RT hat noch eine nette Aussage über das Verhalten von Teilchen zu machen, die analog zum Lagrange-Prinzip der kleinsten Wirkung ist, das ich oben erklärt habe. Da haben wir ja gesagt, dass das Elektron von allen denkbaren Wegen denjenigen nimmt, bei dem die Wirkung minimal wird. In der RT (besonders der ART) kann man das Prinzip umformulieren zum Prinzip der maximalen Eigenzeit: Von allen möglichen Wegen nimmt das Teilchen denjenigen, bei dem seine Eigenzeit maximiert wird.
Für das Elektron vergeht ja auch eine gewisse Zeit zwischen A und B. Nehmt an, es würde einen der Umwege fliegen, die ich oben eingezeichnet habe. Dann wäre es sehr schnell unterwegs, damit es die lange Strecke schafft. Und weil es schnell unterwegs ist, vergeht – wegen der Zeitdilatation – für das Elektron weniger Zeit als wenn es mit konstanter Geschwindigkeit den geraden Weg nimmt. Tatsächlich kann man zeigen, dass die beiden prinzipien (kleinste Wirkung oder maximale Eigenzeit) zueinander äquivalent sind, für einen einfachen Fall habe ich das hier getan.
Viel mehr gibt es über den Weg von A nach B in der Relativitätstheorie nicht zu sagen – sie ändert unser Bild von Raum und Zeit, also die Vorstellung davon, wie die Ereignisse A und B räumlich und zeitlich zueinander angeordnet sind, aber das diskutiere ich hier nicht im einzelnen, denn auch dazu könnt ihr entweder in meiner ART-Serie oder in der oben verlinkten Buchrezension bei Florian mehr nachlesen.
Tja, und wieder einmal bestätigt sich der erste Hauptsatz der Bloggodynamik: Blogartikel werden immer länger, als man denkt. Zugegeben, es war schon sehr optimistisch von mr anzunehmen, ich würde den Weg von A nach B komplett in einem Artikel abhandeln können, aber dass man über die klassische Physik so viel schreiben kann, war mir vorher nicht so klar.
Quantenmechanik und Quantenfeldtheorie vertage ich also – wie so oft – auf einen zweiten (und dritten????) Teil…






Kommentare (27)