Ein Teilchen fliegt von A nach B… Teil 2: Quantenmechanik

In dieser kleinen Serie schaue ich mir das so ziemlich simpelste physikalische Phänomen an, das es gibt: Ein Teilchen (z.B. ein Elektron) fliegt von A nach B. Oder, genauer gesagt, es wird zu einer Zeit am Ort A beobachtet und zu einer späteren Zeit am Ort B (jeweils durch irgendeinen Detektor, über dessen Funktion ich mir keine weiteren Gedanken mache – erstens bin ich Theoretiker und zweitens würde das die Sache nur unnötig komplizieren).

Im ersten Teil habe ich die Sichtweise der klassischen Physik und die der Relativitätstheorie erklärt – das Teilchen hat jeweils eine wohldefinierte Bahn und wenn wir wissen, dass es zwischen A und B kräftefrei ist, dann können wir genau ausrechnen, wo es in der Zwischenzeit war. Zusätzlich habe ich noch zwei andere Sichtweisen der Dinge ins Spiel gebracht, nämlich das Prinzip der kleinsten Wirkung und das der maximalen Eigenzeit.

Das Prinzip der kleinsten Wirkung wird uns nachher im nächsten Teil (jaja, der Artikel ist wie üblich länger als erwartet) in erweiterter Form wieder begegnen, aber erst einmal schauen wir uns an, wie sich das Verhalten des Teilchens beschreiben lässt, wenn wir die Sichtweise der Quantenmechanik in ihrer üblichen Form verwenden.

 Wahrscheinlichkeiten

Während wir in der klassischen Physik wissen, was unser Teilchen zwischen den beiden Beobachtungen bei A und B gemacht hat, können wir in der Quantenmechanik (kurz QM) für die meisten Ereignisse nur Wahrscheinlichkeiten angeben. Ein Teilchen, das wir nicht beobachten, hat eine Wahrscheinlichkeit, an diesem oder jenem Ort zu sein. Erst wenn wir seinen Ort – beispielsweise mit unserem Detektor – messen, dann wissen wir sicher, wo es jetzt gerade ist.

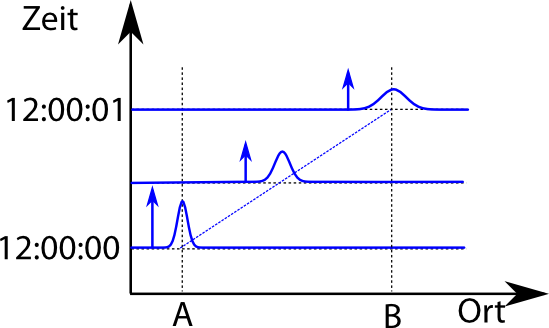
Wenn wir also um 12:00:00Uhr das Teilchen im Detektor A gemessen haben, dann wissen wir sicher, dass es zu diesem Zeitpunkt nirgendwo anders gewesen sein kann. (Auch in der Quantenmechanik kann ein Teilchen nicht an zwei Orten gleichzeitig gefunden werden, wenn man es tatsächlich beobachtet. Was es tut, wenn man es nicht beobachtet, ist eine andere Sache…) Wir können das so veranschaulichen

Die Linie zeigt die Aufenthaltswahrscheinlichkeit dafür an, dass das Elektron irgendwo ist; da es im Detektor A ist, ist die Wahrscheinlichkeit außerhalb des Detektors gleich Null. Innerhalb des Detektors, der ja nicht unendlich klein sein kann,ist es irgendwo, deshalb habe ich dort der Einfachheit halber die Wahrscheinlichkeit überall gleich groß gemacht. (Und wenn man mathematisch pingelig sein will, dann muss man hier von einer Wahrcheinlichkeitsdichte sprechen, damit das Integral darüber gleich 1 ist und man muss – bei einem unendlich genau messenden Detektor – jetzt hier eine delta-Distribution benutzen und lauter so Zeug, aber für “mathematisch pingelig” war ich noch nie bekannt…)

Die Darstellung ist vielleicht etwas gewöhnungsbedürftig, weil die senkrechte Achse eine Doppelfunktion hat: Sie gibt die Zeit an, zu der die Aufenthaltswahrscheinlichkeit angeguckt wird und in der blauen Kurve gibt sie die Wahrscheinlichkeit an.

Mathematisch ist es etwas einfacher, wenn man annimmt, dass der Detektor keine ganz festen Wände hat, sondern dass die Wahrscheinlichkeit, das Elektron irgendwo zu finden, genau am Ort des Detektors am größten ist und dann nach Außen abfällt. Das sieht dann etwa so aus:

Das ändert nicht wirklich viel, macht aber die Darstellung etwas einheitlicher.

Diese Aufenthaltswahrscheinlichkeit ändert sich jetzt mit der Zeit. Sie “zerläuft” nämlich, wird also immer breiter. Das kann man etwa so veranschaulichen:

Ich war hier beim zeichnen etwas schlampig, weil die Fläche unter der Kurve immer die gleiche sein müsste, denn die Fläche entspricht der Gesamtwahrscheinlichkeit, das Teilchen zu finden – dann hätte man aber nix mehr erkannt.

Wie schnell die Wahrscheinlichkeitsverteilung zerläuft, hängt (unter anderem, dazu später mehr) davon ab, wie genau wir das Teilchen vorher festgenagelt haben. (Das ist ein Beispiel für die berühmte Unschärferelation: Wenn man den Ort des Teilchens sehr genau kennt, dann weiß man nicht sehr viel über seine Geschwindigkeit, es kann also bereits nach kurzer Zeit sehr weit weg vom Ursprungsort gefunden werden.) Man kann das, wenn man will, auch berechnen, dafür gibt es die Schrödinger-Gleichung, so ziemlich die wichtigste Gleichung in der Quantenmechanik. Wenn ihr auf den Artikelserien-Link klickt, dann findet ihr dort eine sehr lange ausführliche Erklärung der Gleichung, die brauchen wir heute aber nicht. Für unsere Zwecke reicht es völlig zu wissen, dass die Wahrscheinlichkeitsverteilung zerläuft.

Zum Zeitpunkt 12.00:01 haben wir jetzt also eine ziemlich breite Verteilung.

Jetzt kommt unser zweiter Detektor ins Spiel: Denn zu dieser Zeit – so ja die Vorgabe unseres Experiments – messen wir das Teilchen im Detektor B. Wir wissen jetzt, dass das Teilchen bei B ist, die Wahrscheinlichkeitsverteilung ändert sich also sprunghaft vom Bild oben zu dieser hier:

Das ist der berühmte “Kollaps der Wellenfunktion” (die Wellenfunktion ist eine mathematische Größe, aus der man die Wahrscheinlichkeitsverteilung berechnen kann. Näheres dazu auch in der Schrödinger-Serie.) Sprunghaft ändert sich das, was wir über unser Elektron wissen – eben hätte es noch so ziemlich überall sein können, jetzt aber ist es ganz bestimmt im Detektor B und nirgends sonst.

Ein entscheidender Unterschied zwischen klassischer Physik und Qm ist, dass die klassische Physik deterministisch ist. Es hindert uns niemand, im Detektor A sowohl den Ort als auch die Geschwindigkeit des Teilchens zu messen; wir hätten beispielsweise zwei Detektoren haben könne, die nebeneinander stehen und messen können, wann das Teilchen jeweils durchfliegt. Dann kennen wir die Geschwindigkeit und den Ort zu einer Zeit und können genau vorhersagen, wo das Teilchen wann sein wird. Machen wir das Experiment wieder und wieder und messen immer dieselbe Geschwindigkeit und denselben Ort, so wird das Teilchen auch immer eine Sekunde Später im Detektor B gefunden werden.

In der QM gilt das nicht – wenn wir das Teilchen exakt bei A gemessen haben, dann können wir über seine Geschwindigkeit nichts aussagen (das ist die Unschärferelation) und es gibt nur eine gewisse Wahrscheinlichkeit, dass das Teilchen bei B gefunden wird. Wenn wir das Experiment 1000 mal wiederholen, dann werden wir – trotz identischer Ausgangsbedingungen – das Teilchen vielleicht nur 20 mal bei B messen und die anderen 980 mal nicht. Und wenn wir lauter Detektoren kugelförmig im Abstand von einem Meter um A herum anordnen, dann wird jedesmal ein Detektor das Teilchen finden, aber es gibt keine Möglichkeit, vorherzusagen, wann welcher Detektor anschlägt.

Wellenpakete

Das Bild unseres Teilchens in der Quantenmechanik sieht also vollkommen anders aus als das der klassischen Physik. Das wirft natürlich die Frage auf, warum wir dieses Verhalten von Teilchen im Alltag normalerweise nicht beobachten. Wie funktioniert der Übergang von der Quantenmechanik zur klassischen Physik?

Um das zu verstehen, werfen wir erst mal einen Blick auf die berühmte Unschärferelation. Sie lautet – in der Version, die für uns relevant ist –

Dabei ist Δ x die Ortsunschärfe – das ist nichts anderes als die Breite unseres Wahrscheinlichkeitsberges oben im Bild und somit ein Maß dafür, wie gut wir den Ort des Teilchens kennen. Und Δp ist die Impulsunschärfe, misst also, wie genau wir den Impuls eines Teilchens kennen. Und auf der rechten Seite der Ungleichung steht das berühmte h-quer, das Plancksche Wirkungsquantum geteilt durch 2π.
Der Impuls eines Teilchens ist das Produkt aus seiner Masse und seiner Geschwindigkeit v; wenn wir annehmen, dass wir die Masse kennen und sie m nennen, dann können wir also schreiben

Jetzt kann man Zahlenwerte einsetzen, Beispiele findet man bei Wikipedia (leider hat die Batterie meines Taschenrechners gerade einen tragischen Tod erlitten, und da es sich um einen Rechner mit komischen Knopfzellen handelt, habe ich keine Ersatzbatterien griffbereit). Bei einem Staubkorn kann man problemlos gleichzeitig den Ort auf 10Nanometer und die Geschwindigkeit auf 1Nanometer pro Sekunde genau messen, ohne Ärger mit der Unschärfe zu bekommen. Bei einem Elektron dagegen, dass um viele Größenordnungen (etwa eine Billiarde mal) leichter ist, wäre eine so genaue Orts- und Geschwindigkeitsmessung nicht möglich.

Wie übersetzt sich diese Logik in das Bild unserer Wahrscheinlichkeitsverteilung oben? Die Unschärferelation sagt uns , dass eine sehr enge Lokalisierung eines Elektrons zu einer großen Unkenntnis der Geschwindigkeit führt (während das Problem bei einem schwereren Teilchen weniger dramatisch ist). Diese Unkenntnis der Geschwindigkeit bedeutet aber, dass wir den Ort unseres Teilchens nach kurzer Zeit nur noch sehr ungenau kennen. Je kleiner also die Masse des Teilchens ist, desto schneller “zerläuft” die Wahrscheinlichkeitsverteilung.

Noch ein anderer Aspekt ist wichtig: Oft haben wir ja sowohl eine Information über den Ort, als auch über die Geschwindigkeit eines Teilchens. (Allerdings natürlich immer im Einklang mit der Unschärferelation.) In diesem Fall bewegt sich dann die Wahrscheinlichkeitsverteilung als Ganzes in eine bestimmte Richtung, während sie gleichzeitig immer weiter auseinanderläuft. (Ziemlich ausführlich habe ich das in den Teilen 4-6 meiner Serie zur Schrödingergleichung diskutiert….) Das sieht dann etwa so aus:

Hier habe ich angenommen, dass die Masse unseres Teilchens größer ist, so dass die Verteilung nicht ganz so schnell zerläuft. In blau gestrichelt habe ich die “klassische” Bewegung des Teilchens eingezeichnet. Bei einem Teilchen, das hinreichend viel Masse hat, können wir dann dieses Bild vom Bild der klassischen Physik kaum noch unterscheiden – dort ist die Wahrscheinlichkeit, das Teilchen zu finden, immer genau an einem Punkt gleich 1 (wenn es ein punktförmiges Teilchen ist) und an allen anderen Punkten gleich Null (in rot eingezeichnet):

Ihr seht also, dass die QM zwar prinzipiell andere Vorhersagen macht als die klassische Physik, dass die klassische Physik aber als Grenzfall in der QM enthalten ist.

Zusätzlich kommt noch ein anderer Aspekt hinzu, den ich hier aber nur kurz erwähnen möchte: Ein hinreichend großes Teilchen auf dem Weg von A nach B wird immer mit seiner Umwelt wechselwirken (beispielsweise, wenn Licht darauf fällt). Diese Wechselwirkungen können (vermutlich) als quantenmechanischer Messprozess interpretiert werden, so dass die Wahrscheinlichkeitsverteilung auch zwischen A und B immer wieder zusammenschrumpft, weil das Teilchen beobachtet wurde. (In QM-Experimenten kann man das im so genannten Quanten-Zeno-Effekt ausnutzen.) Weil aber niemand so ganz genau weiß, was ein quantenmechanischer Messprozess ist und weil ich schon mehrfach ausführlich über dieses Problem geschrieben habe, verfolge ich auch diesen Aspekt nicht weiter (unter den Artikelserien findet ihr die Artikel “Die beliebtesten Phrasen…” und “Qm und Realität”, die das ausfürhlich behandeln.) Aber auch hier zeigt sich, dass man – wenn man nur genau genug hinguckt – über ein Teilchen, das von A nach B fliegt, ziemlich viel sagen kann.

Und da das so ist, verschiebe ich den zweiten Teil der quantenmechanischen Betrachtung dann lieber auf den nächsten Teil, denn sonst wird dieser Artikel hier zu lang.