In dieser kleinen Serie schaue ich mir das so ziemlich simpelste physikalische Phänomen an, das es gibt: Ein Teilchen (z.B. ein Elektron) fliegt von A nach B.Im letzten Teil haben wir uns angeschaut, wie man das Verhalten des Teilchens in der Quantenmechanik (QM) beschreibt: Das Teilchen hat eine Aufenthaltswahrscheinlichkeit, die bei einer Messung am Detektor A dort lokalisiert ist und dann zerläuft. Wir haben auch gesehen, wie diese Beschreibung und die der klassischen Physik ineinander übergehen: Wenn das Teilchen hinreichend schwer ist, dann zerläuft seine Aufenthaltswahrscheinlichkeitsfunktion (tolles Wort, oder?) nur vergleichsweise langsam und sie bewegt sich ähnlich wie ein klassisches Teilchen.
Es gibt aber noch eine ganz andere Sichtweise der Dinge – sie ist mathematisch äquivalent zur Beschreibung mit Aufenthaltswahrscheinlichkeiten, ist aber konzeptionell ganz anders gestrickt. Das ist das so genannte “Pfadintegral”.
Um das zu verstehen, müsst ihr noch einmal an den ersten Teil der Serie zurückdenken. Dort haben wir gesehen, dass man in der klassischen Physik das Prinzip der kleinsten Wirkung verwenden kann, um den Weg des Teilchens von A nach B zu beschreiben: Man betrachtet alle denkbaren Wege von A nach B
Der Weg, den das Teilchen tatsächlich geht, ist der mit der minimalen Wirkung. “Wirkung” ist dabei nicht das, was man sich im Alltag darunter vorstellt (der Weg der minimalen Wirkung ist nicht der, bei dem das Teilchen wenig “bewirkt” oder so), sondern einfach ein physikalischer Fachausdruck für eine bestimmte Größe. In unserem einfachen Fall eines Teilchens, das kräftefrei unterwegs ist, ist die Wirkung die Summe über die kinetische Energie zu jedem Zeitpunkt. Mathematisch genauer spricht man vom Integral über die Wirkung (Nachtrag: wie Kommentator Bjoern richtig bemerkt, stimmt das nicht wirklich, es sollte eher Integral über die kinetische Energie oder allgemein über die Lagrangefunktion heißen, aber ich bin hier etwas schludrig) – aber ihr könnt euch einfach vorstellen, dass ihr zu jeder Mikrosekunde einmal die kinetische Energie des teilchens messt und diese ganzen Energien addiert (und am Ende passend normiert, indem ihr durch die Zahl der Messungen teilt, damit immer etwa dasselbe rauskommt, egal ob ihr jede Mikrosekunde oder alle zwei Mikrosekunden messt).
In der klassischen Physik war es jetzt so, dass das Teilchen den Weg mit der kleinsten Wirkung nimmt, fertig. (Falls jemand ganz pingelig sein will: Ein Weg mit extremaler Wirkung geht auch, das ist aber nur selten praktisch relevant.) In der QM sind die Spielregeln etwas komplizierter.Wir haben ja schon im letzten Teil gesehen, dass man in der QM Wahrscheinlichkeitsaussagen macht, keine deterministischen Vorhersagen. Die Wahrscheinlichkeit, dass das Teilchen erst bei A dann bei B gemessen wird, konnten wir über die Wahrscheinlichkeitsverteilung darstellen, die am Anfang (nach der Messung bei A) einen Wert hatte und dann zerlief. Berechnen kann man das mit der Schrödingergleichung, das habe ich aber nicht vorgeführt (zumal es dazu auch ne ganze Artikelserie gibt…).
Auch in unserer neuen Darstellung mit dem Pfadintegral kann man die Wahrscheinlichkeit dafür berechnen, dass das Teilchen von A nach B läuft. Dazu betrachtet man, wie gesagt, jeden möglichen Weg und berechnet dessen Wirkung. Mathematisch kann man das, was hier passiert, sehr elegant mit komplexen Zahlen darstellen (das habe ich z.B. in meiner QFT-Serie auch so gemacht), aber anschaulicher ist es, man hantiert mit kleinen Pfeilen.
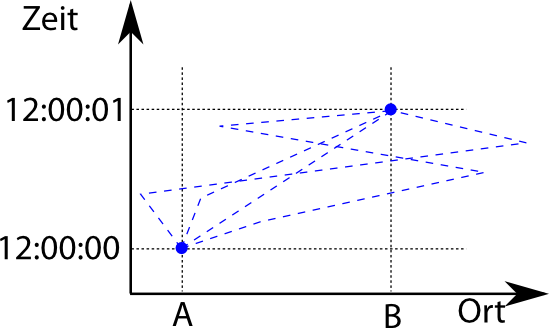
Jeder mögliche Weg von A nach B bekommt also einen kleinen Pfeil zugeordnet, den ihr euch wie einen Zeiger an einer Uhr vorstellen könnt.. Am Anfang (um 12:00:00 bei A) zeigt der Pfeil für alle Wege genau nach rechts. (Ihr könnt ihn auch woanders hinzeigen lassen, das ist egal – Hauptsache, ihr macht es für alle Wege gleich.) Jetzt verfolgt ihr den gerade betrachteten Weg von A nach B und lasst den Pfeil dabei rotieren (typischerweise gegen den Uhrzeigersinn). Wie schnell der Pfeil zu einem bestimmten Zeitpunkt rotiert, hängt von der Wirkung ab – teilt die Wirkung durch das Plancksche Wirkungsquantum h, und ihr erhaltet den Wert der Rotationsgeschwindigkeit (in Einheiten von Radiant pro Sekunde, falls es jemand genau wissen will). Ihr lauft also den Weg des Teilchens ab und lasst den Pfeil rotieren, und zwar um so schneller, je größer die Wirkung jeweils ist. (Nachtrag: wieder etwas schludrig, genauer ist es das Wirkungsinkrement oder die Lagrangefunktion, siehe den Kommentar unten) Das kann man sich etwa so veranschaulichen (das Bild ist nur qualitativ zu verstehen, ich habe nichts wirklich durchgerechnet und für ein reales Teilchen dreht sich der Pfeil viele viele Millionen mal in der Sekunde):
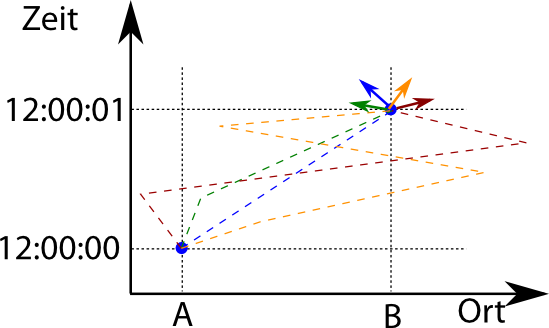
Das tut ihr jetzt für jeden der möglichen Pfade von A nach B. Am Ende habt ihr dann also jeden denkbaren Pfad von A nach B genommen und zu jedem gehört ein Pfeil, der in eine Richtung zeigt (statt unendlicher vieler Pfade zeichne ich nur vier):
Jetzt hängt ihr alle diese Pfeile hintereinander, also immer den Startpunkt des einen Pfeils hinter den Endpunkt des vorigen Pfeils. (Weil das unendlich viele Pfeile sind, ist diese Operation mathematisch etwas trickreich, aber das muss euch nicht stören, weil es hier nur um die Anschauung geht.) Das gibt dann einen Gesamtpfeil (in schwarz):
Als nächstes zeichnet ihr ein Quadrat, dessen Kantenlänge gleich der Länge des Gesamtpfeils ist:
Und jetzt kommt der Trick des Ganzen: Die Fläche dieses Quadrats gibt euch die Wahrscheinlichkeit dafür, dass das Teilchen von A nach B fliegt. Das ist alles. (Diese ganze Erklärung mit den Pfeilen stammt übrigens von Feynman aus dem Buch “QED – the strange theory of light and matter”.)
Auch wenn die Prozedur auf den ersten Blick etwas kompliziert aussieht, ist sie konzeptionell doch sehr einfach: Ihr betrachtet alle Möglichkeiten, wie das Teilchen von A nach B kommen kann. Jeder dieser Möglichkeiten ordnet ihr einen Pfeil zu, dessen Drehwinkel durch die Wirkung auf diesem Weg gegeben ist. Alle diese Pfeile hängt ihr hintereinander und bekommt direkt die Wahrscheinlichkeit dafür, dass der Prozess stattfindet.
Pfadintegrale und die klassische Physik
Auch bei den Pfadintegralen kann man wieder die Verbindung zur klassischen Physik herstellen – dort war es ja so, dass sich das teilchen auf dem Weg mit der kleinsten Wirkung bewegt – das ist also der, bei dem sich der Pfeil am wenigsten gedreht hat. In der QM sollte also dieser Weg zum Endergebnis am stärksten beitragen, wenn es sich um ein Teilchen handel,t das man mit den Mittel der klassischen Physik beschreiben kann.
So ist es auch tatsächlich: Für ein solches Teilchen ist die Wirkung ja viel viel größer als das Plancksche Wirkungsquantum h. Das bedeutet, dass die Drehgeschwindigkeit des Pfeils sehr groß ist – der Pfeil dreht sich also auf jedem Weg von A nach B sehr sehr oft herum, bis er in seiner Endstellung ankommt.
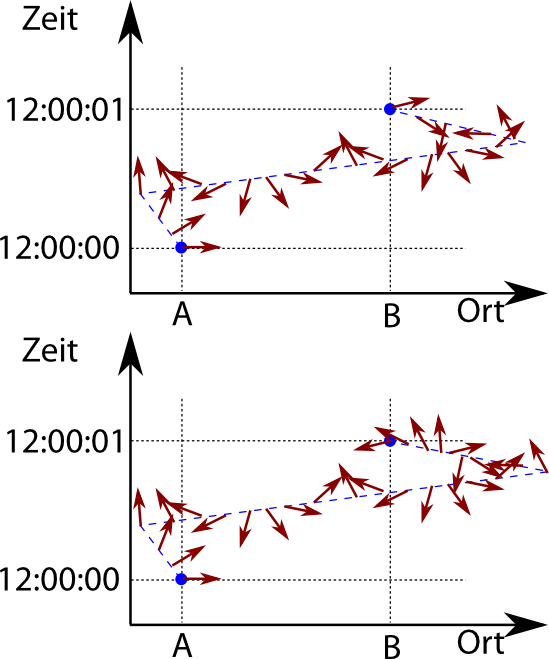
Betrachten wir jetzt einen beliebigen Weg von A nach B (nicht den mit der kleinsten Wirkung, sondern einen anderen). Wenn sich der Pfeil extrem schnell dreht, dann muss ich diesen Weg nur ein klein wenig verändern (im zweiten Bild habe ich ihn rechts ein Stückchen länger gemacht, das lässt sich am schnellsten zeichnen), und ich bekomme einen Weg, bei dem der Pfeil genau in die entgegengesetzte Richtung zeigt:
Die Pfeile dieser beiden Wege tragen also zum Endergebnis nichts bei, weil sie sich gegenseitig aufheben.
Hmm – aber gilt das dann nicht für alle Wege? Dann heben sich alle Pfeile immer gegenseitig weg und die Wahrscheinlichkeit ist immer null, weil alle Pfeile sich aufheben. Teilchen können sich also nie von A nach B bewegen (egal wo A oder B ist) – das scheint nicht so ganz korrekt zu sein, oder?
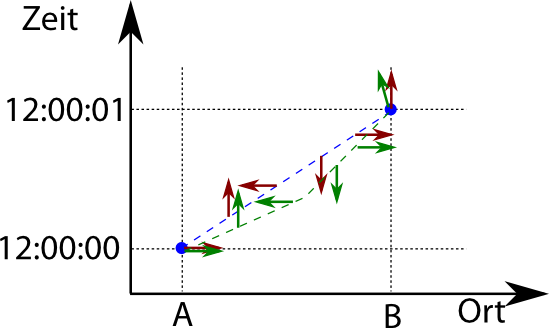
Ist es auch nicht – es gibt nämlich einen Weg, bei dem das Argument nicht gilt: Den Weg mit der kleinsten Wirkung. Betrachtet diesen Weg, zu dem ein entsprechender Pfeil gehört. Als nächstes betrachten wir zwei Wege, die zu diesem fast identisch sind – damit ist ihre Wirkung auch fast identisch (mathematisch liegt das daran, dass wir das Minimum der Wirkung betrachten, und in der Nähe des Minimums verschwindet ja die erste Ableitung). Die Pfeile dieser Wege zeigen also fast in dieselbe Richtung. Hier einer der beiden Pfade; weil er etwas länger ist, rotiert der Pfeil ein klein wenig weiter, aber nicht sehr viel (ich zeichne nur einen, sonst wird’s unübersichtlich, und ich bin mit den Farben der Pfeile nicht ganz konsequent gewesen, ich hoffe das verwirrt nicht…):
Der Pfeil dieses Pfades und der des Weges mit kleinster Wirkung heben sich also nicht weg, sondern verstärken sich. Deswegen wird in diesem Fall die Wahrscheinlichkeit vom Pfad mit der kleinsten Wirkung dominiert.
Weichen wir stärker vom Weg minimaler Wirkung ab, dann finden wir natürlich auch einen Weg, dessen Pfeil dem des Weges mit der kleinsten Wirkung entgegengesetzt ist, aber zu diesem Weg finden wir dann wieder einen, der dessen Pfeil kompensiert. Insgesamt ergibt sich also ein großer Beitrag von solchen Wegen, bei denen die Wirkung (fast) minimal ist und damit wieder genau das Bild der klassischen Physik. Ausführlich habe ich das übrigens auch in meiner QFT-Serie diskutiert.
Energie- und Impulserhaltung
Die Darstellung mit Pfadintegralen (und später dann die mit Feynman-Diagrammen) führt immer wieder zu Verwirrung, weil die einzelnen Pfade, die wir hier betrachten, ja ziemlich seltsam sind: Das Teilchen fliegt einfach so im Zickzack und ändert dabei seine Geschwindigkeit. Was ist denn mit der Energie- und der Impulserhaltung? Gelten die in der QM nicht mehr? (Das glauben viele Leute, weil es ja auch die Unschärferelation gibt – wenn man den Impuls nicht genau bestimmen kann, dann kann er ja wohl auch nicht exakt erhalten sein, oder?) Um das zu verstehen, muss man etwas genauer hinschauen.
Warnung: Das was ich jetzt schreibe, habe ich in genau dieser Form in keinem Physikbuch diskutiert gefunden; es gibt ein paar Diskussionen beim Physikforum, in denen diese Problematik besprochen wird und ich bin mir ziemlich sicher, dass es stimmt, aber bevor ihr es in eurer Masterprüfung so wiedergebt, solltet ihr vielleicht nochmal die Prüferin fragen. Ich bin mir auch nicht ganz sicher, ob das, was ich hier schreibe, wirklich verständlich (oder gar allgemeinverständlich) ist – beschwert euch im Zweifel in den Kommentaren.
Im folgenden betrachte ich nur die Impulserhaltung; für die Energieerhaltung geht das Argument letztlich genauso (und in der QFT sorgt die Relativitätstheorie dafür, dass Energie und Impuls nur zwei Aspekte derselben Sache sind).
Wir haben also um 12:00:00 unser Teilchen bei A gemessen. Betrachten wir einen der möglichen Pfade von A nach B, und zwar einen Zickzackpfad. Wenn das Teilchen diesen Pfad nimmt, dann ist während des Wegs von A nach B der Impuls nicht erhalten, weil das Teilchen ja seine Geschwindigkeit abrupt ändert. Trotzdem trägt dieser Pfad zur Gesamtwahrscheinlichkeit bei. Solange wir allerdings nur den Ort des Teilchens bei A und B messen, wissen wir über seinen Impuls vorher und hinterher nichts, insofern können wir kein direktes Problem mit der Impulserhaltung feststellen, weil wir den Impuls ja nicht kennen.
Probieren wir also etwas anderes: Wir geben dem Teilchen am Anfang (bei 12:00:00Uhr) einen genau bekannten Wert des Impulses. Damit ist sein Aufenthaltsort allerdings – wegen der Unschärfe – vollkommen unbestimmt. Messen wir den Impuls des Teilchens um 12:00:01 erneut, so messen wir exakt denselben Wert, die Impulserhaltung ist gewährleistet. Das liegt daran, dass die Aufenthaltswahrscheinlichkeit sich zeitlich nicht ändert (wer’s gern mathematisch ausdrückt: Der Impulseigenzustand ist auch ein Energieeigenzustand und deshalb bis auf einen Phasenfaktor zeitlich konstant.)
Wie beschreiben wir den Zustand mit festem Impuls im Pfadintegral-Bild? Das ist auf den ersten Blick nicht so einfach, denn wir sind ja immer an einem Ort (A) losgelaufen und an einem anderen Ort (B) geendet – jetzt aber wissen wir den Ort nicht, sondern kennen nur den Impuls am Anfang und am Ende. Wir können aber nach den Regeln der QM den Zustand mit festem Impuls am Anfang als eine Überlagerung aus lauter Zuständen ansehen, bei denen das Teilchen an einem bestimmten Ort ist. (Das mit den Überlagerungen habe ich in meiner QM-Serie ausführlicher erklärt.)
Wir betrachten also den Zustand unseres Teilchens mit festem Impuls zur Zeit 12:00:00 als eine Überlagerung aus Zuständen, an denen das Teilchen an jeweils einem Ort ist. Genauso betrachten wir den Zustand zur Zeit 12:00:01 mit festem Impuls ebenfalls als eine Überlagerung aus allen denkbaren Ortszuständen. Die Gesamtwahrscheinlichkeit, dass ein teilchen mit einem bestimmten Impuls zur Zeit 12.00:00 zu einem teilchen mit einem bestimmten Impuls zur zeit 12.00:01 wird, ergibt sich jetzt als Überlagerung aller Möglichkeiten, von jedem der denkbaren Startpunkte zu jedem der denkbaren Endpunkte zu kommen. Eine dieser Möglichkeiten ist unser alter Bekannter: Der Weg von A nach B. Die Wahrscheinlichkeit für diesen Weg wiederum können wir berechnen, indem wir alle denkbaren Möglichkeite, von A nach B zu kommen, aufaddieren, so wie wir es oben gemacht haben. Das gleiche müssen wir aber auch für alle anderen denkbaren Kombinationen von Start- und Zielpunkt tun, weil ja alle möglichen Start- und Zielpunkte beitragen.
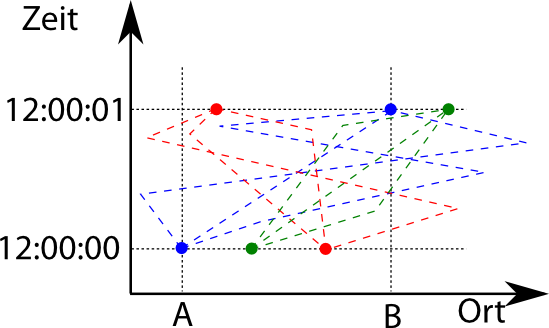
Wir haben jetzt also eine komplizierte Dreifachsummierung: Den Anfangs- und den Endzustand beschreiben wir jeweils als Überlagerung aus einzelnen Ortszuständen, und für jede denkbare Kombination betrachten wir dann noch alle möglichen Wege. Das kann man vielleicht etwa so veranschaulichen:
Es werden also alle Wege von allen möglichen Start- zu allen möglichen Endpunkten jeweils überlagert und dann am Ende alles aufsummiert. Da kann einem beim Hinschauen schon etwas schwummrig werden – aber zum Glück ist die Mathematik der ganzen Angelegenheit wesentlich einfacher, als man vielleicht denkt: Am Ende überlagern sich nämlich alle denkbaren Möglichkeiten genau so, dass die Wahrscheinlichkeit dafür, dass der Impuls des Teilchens um 12.00:01 derselbe ist wie der um 12.00:00, genau gleich 1 ist, und alle anderen Möglichkeiten haben die Wahrscheinlichkeit Null. Einzelne Wege von A nach B scheinen also die Impulserhaltung zu verletzen, aber die Überlagerung der einzelnen Wege ist ja nur unsere Art, den Prozess zu beschreiben – physikalisch relevant ist nur das Endergebnis. Deswegen finde ich es auch etwas unglücklich, wenn manche Leute – wie David Deutsch in seinem Buch “Fabric of Reality” – sagen, dass das Teilchen in unterschiedlichen Paralleluniversen existiert, die dann miteinander wechselwirken. Keins dieser “Paralleluniversen” ist für sich genommen physikalisch zulässig. Wenn man den Prozess bildlich beschreiben will, dann kann man natürlich sagen: “Das Teilchen geht alle Wege gleichzeitig mit allen denkbaren Geschwindigkeiten und interferiert am Ende mit sich selbst, so dass die Wahrscheinlichkeit des Endzustands herauskommt”. (So ähnlich formuliert es auch Feynman im oben erwähnten QED-Buch.) Aber das ist eben eine anschauliche Beschreibung unserer Rechenvorschrift, nicht unbedingt eine anschauliche Beschreibung dessen, was im Universum “tatsächlich” passiert – wie man schon daran sehen kann, dass man das Teilchen ja auch ohne den Pfadintegral-Formalismus beschreiben kann, so wie wir es im letzten Teil getan haben. Es ist durchaus nützlich, beide Bilder parat zu haben; manchmal ist das eine praktischer und anschaulicher, manchmal das andere. Aber wie die Natur “wirklich” ist, können wir nicht sagen.
Falls ihr jetzt denkt, dass mit diesem Fazit alles gesagt wäre, was man zum Thema “Ein Teilchen fliegt von A nach B” sagen kann – nein. Aber den 4. (und vermutlich 5. (oder gar 6.???)) Teil dieser Serie verschiebe ich dann ins nächste Jahr (in dem auch noch die im Sommer begonnene Serie zum Vakuum weitergehen sollte).
Für dieses Jahr aber war’s das.
Allen Leserinnen und Lesern einen guten Rutsch und alle guten Wünsche für 2014.









Kommentare (43)