Ein Teilchen fliegt von A nach B… Teil 4 Quantenfelder und Unendlichkeiten

In dieser kleinen Artikelserie passiert wirklich nichts Aufregendes – ein Teilchen fliegt von A nach B. Aber je tiefer man in die Physik einsteigt, desto komplexer wird dieser unglaublich einfache Prozess: In der klassischen Physik fliegt das Teilchen einfach von A nach B, in der Quantenmechanik haben wir plötzlich (in der üblichen Formulierung) Warhscheinlichkeitsverteilungen, die sich zeitlich entwickeln, und wenn wir das Bild des Pfadintegrals verwenden, dann können wir unser Teilchen so beschreiben, als würde es alle denkbaren Wege mit allen denkbaren Geschwindigkeiten gleichzeitig nehmen und am Ende alle diese Wege miteinander interferieren lassen.

Und als ob das noch nicht genug wäre, geht es noch komplizierter, wenn wir berücksichtigen, dass unser Teilchen auch noch mit anderen Teilchen wechselwirken kann.

Moment – wieso wechselwirken? Sollte unser Teilchen nicht einfach durchs Vakuum fliegen (mal abgesehen von den beiden Detektoren)? Ja, sollte es. Aber das Vakuum ist ja auch nicht mehr das, was es mal war, sondern ein nicht ganz unkompliziertes Gebilde. (Und, ja, ich weiß, dass in meiner Vakuum-Serie auch noch mindestens ein Teil aussteht – hat jemand Lust, mir ne Vollzeitanstellung als Blogger zu finanzieren?) Wenn also ein Teilchen durch die Gegend fliegt, dann kann unterwegs alles mögliche passieren (und alle diese Möglichkeiten müssen wir am Ende, wie beim Pfadintegral in der QM, miteinander interferieren lassen).

Machen wir die Sache etwas konkreter und nehmen als Teilchen, das von A nach B fliegt, ein Elektron. Ich betrachte hier zunächst einmal nur die Theorie der Quantenelektrodynamik; unser Elektron darf also nur mit Photonen, den Teilchen des Lichts, wechselwirken.

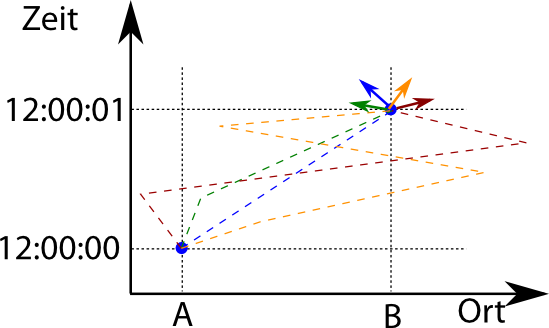
Im letzten Teil haben wir den Weg des Elektrons von A nach B als Überlagerung über alle denkbaren Wege beschrieben, etwa so:

Zu jedem denkbaren Weg gehört dabei ein Pfeil und am Ende muss man alle diese Pfeile hintereinanderhängen, um die Gesamtwahrscheinlichkeit herauszubekommen, dass das teilchen von A nach B fliegt.

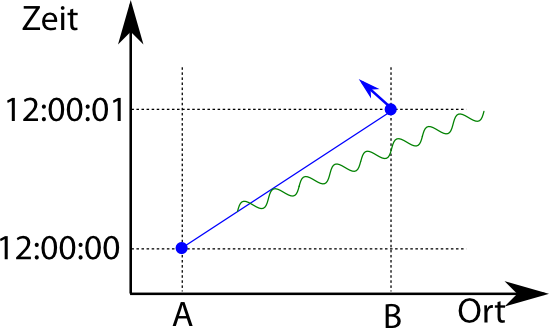
Jetzt aber kommt noch hinzu, dass unser Elektron auf jedem dieser Wege auch noch etwas anderes tun kann, als einfach irgendwo herumzufliegen – es kann zum Beispiel ein Photon aussenden:

Geht das wirklich so? Nein, eigentlich nicht. Betrachten wir wieder den Fall, dass unser Elektron am Anfang einen bestimmten Impuls hat. Damit liegt auch seine Bewegungsenergie fest, denn Impuls ist (bei nicht-relativistischen Geschwindigkeiten) Masse mal Geschwindigkeit und die Bewegungsenergie ist ein-halb mal Masse mal Geschwindigkeit ins Quadrat.Wenn unser Elektron jetzt ein Photon mit einer bestimmten Energie aussendet, dann verringert sich die Energie des Elektrons um diesen Betrag und entsprechend verringert sich auch seine Geschwindigkeit und damit sein Impuls. Damit die Impulserhaltung gelten kann, müsste dieser Impuls jetzt auf das Photon übertragen werden. Dummerweise gibt es aber auch für Photonen eine eindeutige Beziehung zwischen Energie und Impuls – und die Formeln passen nicht so zusammen, dass unser Photon sowohl den fehlenden Impuls als auch die fehlende Energie des Elektrons übernehmen könnte. Ein frei herumfliegendes Elektron kann also kein Photon einfach so aussenden, dann könnten wir am Ende den Impuls von Elektron und Photon und deren Energien messen und eine Verletzung der Impuls- oder Energieerhaltung bekommen.

Was es aber tun kann, ist, das Photon erst auszusenden und dann wieder zu absorbieren. (Ihr solltet euch inzwischen nicht mehr darüber wundern, dass ein Photon ausgesandt und wieder eingefangen werden kann – auch für das Photon müssen alle denkbaren Wege berücksichtigt werden, nicht nur die, bei denen es brav mit konstanter Lichtgeschwindigkeit fliegt. Wenn wir Zustände mit festem Impuls betrachten, dann ist der Aufenthaltsort unserer Teilchen eh nicht festgelegt, sondern sie sind über den ganzen Raum “verschmiert”.)

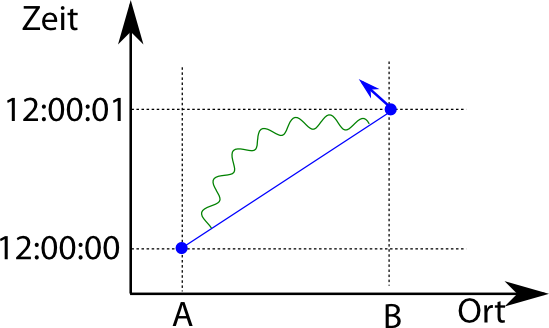
Ich zeichne das mal so, obwohl ich hier jetzt wieder ein Elektron habe, das mit eindeutigem Ort losfliegt (also keinen eindeutigen Impuls hat):

“Wie soll das denn gehen?” fragt ihr euch jetzt vielleicht. Zwischendrin hat doch das Elektron ein Photon ausgesendet und damit haben wir doch ein Problem mit der Energie- und Impulserhaltung, oder nicht? Nein, überraschenderweise haben wir das nicht, aber die Physik ist hier trotzdem seltsam. Nachdem das Elektron das Photon ausgesandt hat, hat es seine Energie und seinen Impuls geändert und das Photon trägt genau diese Energie und diesen Impuls weg (bringt beide aber bei der Absorption brav wieder zurück). Die Energie- und Impulserhaltung ist also gewährleistet.

“Moment, du hast doch gerade erklärt, dass das nicht geht, weil die Energie-Impuls-Beziehungen nicht passen!” beschwert ihr euch als nächstes, richtig? Recht habt ihr – aber unser Elektron und unser Photon haben im Moment (also zwischen dem Aussenden und dem Einfangen des Photons) einfach nicht die richtige Beziehung zwischen Energie und Impuls. Das Elektron kann zum Beispiel einen riesigen Impuls und eine sehr kleine kinetische Energie haben (oder umgekehrt). Solche Teilchen, bei denen die Energie-Impuls-Beziehung nicht passt, nennt man virtuelle Teilchen, dazu habe ich letztes Jahr schon etwas geschrieben.

Allerdings ist wieder mal Vorsicht geboten: Wir haben hier einen einzigen Prozess betrachtet, bei dem das Elektron ein Photon aussendet. tatsächlich muss man aber wieder einmal alle Möglichkeiten berücksichtigen, wie das Elektron ein (oder auch mehrere) Photonen aussenden und wieder einfangen kann.

Diagramme dieser Art nennt man übrigens auch Feynman-Diagramme.

Anmerkung für PhysikerInnen: Man kann Feynman-Diagramme im Orts- oder im Impulsraum lesen. Normalerweise bezeichnet man die Achsen im Diagramm ja einmal als Orts- und einmal als Zeit-Achse. Die Vertices, wo Teilchen absorbiert oder emittiert werden, liegen dann an einem bestimmten Ort. Um alle Möglichkeiten zu berücksichtigen, muss man dann aber über alle denkbaren Orte integrieren. Tut man das für den Fall, wo alle ein- und ausfliegenden Teilchen in Impulseigenzuständen sind, dann sorgt die Integration über den Ort gerade dafür, dass man die Fouriertransformierte der Delta-Distribution für den Impuls bekommt. Mit anderen Worten: Die Integration über den Ort (und die Zeit) sorgt genau für die Erhaltung des Impulses (und der Energie) an jedem Vertex. Die Rechnung dazu steht vermutlich in jedem QFT-Buch der Welt, nicht alle machen sich aber die Mühe, die doppelte Interpretation von Feynmandiagrammen (lesbar im Orts- oder im Impulsraum) explizit zu erwähnen, was zumindest bei mir immer zu massiver Verwirrung geführt hat.  (Ende der Anmerkung)

Wir müssen  für unser Elektron auf seinem Weg von A nach B nicht nur alle denkbaren Wege überlagern, sondern auch noch alle Möglichkeiten, wie das Elektron unterwegs ein (oder auch mehrere) Photonen aussenden kann, wobei dann zwischendurch aus dem Elektron ein “virtuelles” Elektron wird, bei dem die Energie-Impuls-Beziehung nicht passt. Solche Teilchen nennt man auch Teilchen, die “nicht auf der Massenschale liegen” oder kurz “off-shell”-Teilchen. (Der Begriff “Massenschale” stammt aus der Relativitätstheorie und drückt gerade die Verknüpfung zwischen Energie und Impuls aus. Das erkläre ich jetzt aber nicht auch noch (hätte ich klugerweise im ersten Teil machen können, da habe ich aber nicht dran gedacht…))

Unendlichkeiten, Renormierung und all  das

“Gut”, sagt ihr vermutlich, “dann rechnen die Physikerinnen diese ganzen Wechselwirkungen eben auch noch mit aus, das wird ja vermutlich auch nicht schlimmer sein, als das, was wir bisher gemacht haben.” Aber leider ist dieser Optimismus nicht wirklich gerechtfertigt.

Wir müssen ja (wie im letzten Teil erklärt) einen Pfeil für jede Möglichkeit berechnen, mit dem wir den Beitrag des einzelnen Pfades bewerten, und am Ende alle diese Pfeile zu einem Gesamtpfeil addieren, aus dem wir dann die Wahrscheinlichkeit des Prozesses berechnen. Rechnet man nun aus, wie schnell sich dieser Pfeil dreht, wenn man den Prozess mit dem ausgesandten und wieder eingefangenen Photon berücksichtigt, dann kommt man auf einen mathematisch eindeutigen, aber physikalisch ziemlich unhandlichen Wert: Unendlich.

Das ist das berühmte Problem der Unendlichkeiten in der Quantenfeldtheorie, von dem ihr vielleicht schon mal gehört habt. Es hat die Physikerinnen etwa 20 Jahre lang beschäftigt, bis Ende der Vierziger Jahre die richtigen Werkzeuge zur Verfügung standen, um mit diesen Unendlichkeiten fertig zu werden.

Ohne viel Mathematik zu betreiben (die Mathematik ist hier wirklich etwas hässlich, da wimmelt es von fiesen Integralen und Dinge werden in 4-plus-ein-bisschen Dimensionen berechnet, um die Unendlichkeiten sauber fassen zu können und lauter so Zeug, das mich nach wie vor verwirrt, aber mir geht es nur darum, euch eine Idee zu geben, was passiert), also, auch ohne viel Mathematik könnt ihr leicht einsehen, warum hier Unendlichkeiten ins Spiel kommen können. Unsere virtuellen teilchen waren ja “off-shell” – Energie und Impuls können beliebige Werte annehmen, solange nur die Gesamtsumme passt, so dass der Impuls (und die Energie) erhalten ist.  Und beliebige Werte sind eben auch sehr sehr große Werte – theoretisch kann die Energie eines virtuellen Teilchens oder sein Impuls größer sein als die des gesamten beobachtbaren Universums oder aller denkbaren Multiversen zusammengezählt oder noch viel mehr.

Ist das nicht ziemlich unsinnig? Anzunehmen, dass jedes Elektron, das von A nach B fliegt, zwischendurch mal einen Weg geht auf dem seine Energie so groß ist, dass sie größer ist als die des Universums? Und müsste so ein Prozess nicht dazu führen, dass sich unterwegs dann ein Schwarzes Loch bildet (weil wir so irre viel Energie haben), das den ganzen Prozess kaputt macht? (Das ist eine wirklich gute Frage, auf die wir ohne eine Theorie der Quantengravitation aber wohl keine Antwort haben.) Irgendwo muss ja wohl auch mal eine Grenze für die Energie (oder den Impuls) erreicht sein, oder?

Richtig. Und diese Erkenntnis ist tatsächlich der Schlüssel dazu, mit den Unendlichkeiten fertig zu werden: Wir müssen die Energien und die Impuls begrenzen (Ursprünglich hat man das, was jetzt kommt, als rein mathematisches Werkzeug angesehen (eine so genannte “Regularisierung”), aber der Trend geht heutzutage immer mehr dahin, die Unendlichkeiten als künstlich anzusehen, weil irgendwo eine fundamentalere Theorie, die wir noch nicht haben, die Energien sauber begrenzen sollte.)

Wir nehmen also an, dass es einen maximalen Impuls für unsere virtuellen Teilchen gibt (und genauso eine maximale Energie, ich schreibe das jetzt nicht immer hin). Wenn wir das tun und dann den Beitrag unseres Prozesses zur Drehung unseres Pfeils berechnen, dann kommt ein irrsinnig großer, aber endlicher Wert heraus. Wie groß der Wert genau ist, hängt davon ab, wo wir den Grenz-Impuls ansetzen. Wie groß dieser Wert tatsächlich ist, hängt sicher davon ab, welchen Gültigkeitsbereich unsere Theorie hat, die wir gerade betrachten (die Quantenelektrodynamik) – aber solange wir die fundamentalere Theorie nicht haben, wissen wir das ja nicht. “Mist!”, wie mein Lieblingsbrot sagen würde.

Aber wir können uns aus diesem Sumpf herausziehen, wenn wir uns erinnern, dass wir hier Physik betreiben – nicht bloß theoretische Physik, sondern echte Physik, die auch messbare Konsequenzen hat. Was wissen wir denn experimentell und aus den Überlegungen der letzten Teile?

Wir wissen, dass Elektronen von A nach B fliegen können und aus der QM wissen wir auch ziemlich genau, wie schnell sich der Amplitudenpfeil des Elektrons auf diesem Weg dreht. Das hing ja – ihr erinnert euch vielleicht noch – von der kinetischen Energie zu jedem Zeitpunkt ab und in die geht die Masse ein. Diese Masse können wir experimentell auf verschiedene Weise bestimmen, aber eine Möglichkeit besteht genau darin, zu sehen, wie das Elektron von A nach B kommt. Im zweiten Teil haben wir ja auch – in der anderen Darstellung der QM – gesehen, dass es von der Masse eines Teilchens abhängt, wie schnell seine Wahrscheinlichkeitsverteilung zerläuft. So oder so – in der Quantentheorie hat die Masse eines teilchens etwas damit zu tun, wie es von A nach B kommt; ausgedrückt entweder durch das Zerlaufen der Wahrscheinlichkeitsverteilung oder durch die Drehung des kleinen Pfeils.

Wenn wir jetzt zusätzlich die Möglichkeit berücksichtigen, dass das Elektron unterwegs noch Photonen aussenden kann, dann wissen wir schon, wie sich das am Ende auf die Ergebnisse auswirken muss: Gar nicht. Denn die Masse des Elektrons, die die Bewegung bestimmt, haben wir experimentell gemessen und der Wert, den wir da herausbekommen haben, muss der Wert sein, der am Ende aller Rechnungen auch in unserer Quantenelektrodynamik herauskommt. Der gemessene Wert der Elektronenmasse muss also den Einfluss des Photon-Aussende-Prozesses (und aller anderen denkbaren Prozesse) schon enthalten.

Findet ihr das verwirrend? Falls ja, kann ich euch beruhigen: Ist es auch. Es ist deswegen verwirrend, weil wir mit zwei unterschiedlichen Konzepten von “Masse” hantieren: Das eine ist die experimentell bestimmte Masse, die wir bekommen, wenn wir beobachten, wie unser Teilchen von A nach B fliegt. Das andere ist die “theoretische” Masse, die als Zahl in unsere Gleichungen für die Quantenelektrodynamik eingeht. Diese Zahl selbst ist keine beobachtbare Größe – beobachten können wir nur die experimentelle Masse. Die experimentelle und die theoretische Masse sind nicht identisch, weil in die experimentelle Masse auch noch der Prozess eingeht, bei dem das Elektron unterwegs ein Photon aussendet und dann wieder einfängt. (Und falls jemand fragt, wie das nun wieder mit der Relativitätstheorie und der Gravitation zusammenhängt – die schwere Masse des Elektrons ist auch die, in der alle diese Effekte schon drin sind.)

Oft spricht man bei der theoretischen Masse auch von der “nackten” Masse, weil es eben die Masse ohne alles ist, also ohne zusätzliche Effekte durch Photonenaussendung und so. Die experimentelle Masse heißt oft “effektive Masse”, weil es die ist, die sich am Ende (also “effektiv”) ergibt, wenn man alle Effekte berücksichtigt. (Ein ähnliches Phänomen gibt es übrigens in der Festkörperphysik: Elektronen in einem Kristallgitter benehmen sich fast wie freie Elektronen, aber die Wechselwirkung mit dem Kristallgitter äußert sich darin, dass sich ihre Energie-Impuls-Beziehung ändert. Das erkläre ich übrigens ausführlich in meinem demnächst hoffentlich erscheinenden Buch zu meiner Vorlesung.)

Wie groß der Unterschied zwischen experimenteller und theoretischer Masse ist, hängt davon ab, wo wir unseren Wert für den Grenzimpuls annehmen, je größer der ist, desto größer ist der Unterschied. (Und wenn wir beliebig große Impulse zulassen, dann wird der Unterschied unendlich groß.) Was man jetzt mathematisch trickst ist das Folgende: Man berechnet, wie groß der Unterschied zwischen der experimentellen und der theoretischen Masse ist, und zwar abhängig von dem Wert des Grenzimpulses (auch gern als “cutoff” bezeichnet) und schreibt die Gleichungen mit diesem Wert der theoretischen Masse, so dass sichergsetellt ist, dass nach Einbeziehen der Photon-Aussendung die experimentell gemessene Masse rauskommt. Und dann zeigt man, dass man den Massenterm für beliebige Werte des cutoffs so anpassen kann, dass immer die experimentell beobachtbare Masse herauskommt. (Mathematisch klappt das sogar mit einem Grenzübergang für unendlich große cutoffs, aber physikalisch ist das – wie oben angemerkt – vermutlich nicht wirklich sinnvoll.) Damit ist sichergestellt, dass die Theorie funktioniert – wir wissen zwar nicht, wo der cutoff liegt, aber wir können immer sicherstellen, dass am Ende eine Übereinstimmung mit dem Experiment herauskommt.

Mir ist gerade eine Analogie eingefallen, ich weiß nicht, ob die euch weiterhilft, aber ich versuch’s mal damit: Stellt euch vor, ein reicher Erbonkel vermacht euch einen Prozentsatz seines Vermögens. Leider wisst ihr nicht, wie groß der Prozentsatz ist (1%, 10%, 99%?), und ihr wisst auch nicht, wie groß sein Vermögen tatsächlich ist. Irgendwann bekommt ihr dann von der Kanzlei Fish&Cage eine Überweisung über eine Million Euro, euer effektives Erbe. Wenn ihr 1% bekommen habt, dann betrug das Vermögen des Onkels 100Millionen, wenn es 10% waren, 10 Millionen und so weiter. Abhängig vom Wert des Prozentsatzes (des cutoffs) könnt ihr das wahre, unbeobachtbare (“nackte”) Vermögen berechnen.

Diesen Trick, mit dem man die Theorie rückwärts an die Beobachtung anpasst, nennt man “Renormierung”. Ist ein etwas blöder Name, weil wir ja noch gar nicht “normiert” haben, also können wir es auch nicht “renormieren”, aber geeignet gewählte Worte sind ja nicht immer die Stärke der PhysikerInnen. Im Englischen heißt der Prozess übrigens “renormalisation” und manchmal liest man dann im Deutschen das Wort “Renormalisierung”, das ist aber falsch und ein Zeichen dafür, dass jemand falsch rückübersetzt.

Genau so, wie wir es hier für die Masse gemacht haben, muss man auch andere Größen “renormieren”, beispielsweise die elektrische Ladung. Generell gilt, dass jede Größe, die in die fundamentalen Gleichungen einer Quantenfeldtheorie eingeht, renormiert werden muss, um Theorie und Experiment zusammenzubringen.

Der Trick mit der Renormierung klappt allerdings nicht immer – manche Theorien sind nicht renormierbar, es gibt also keinen mathematisch sauberen Weg, die Unendlichkeiten (oder die Abhängigkeit vom cutoff) sauber rauszubekommen. Solche Theorien sind dann physikalisch nicht sinnvoll. Ein Beispiel dafür ist die Quantengravitation: Einfache Ansätze, die allgemeine Relativitätstheorie zu einer Quantentheorie zu machen, scheitern genau an diesem Problem. Auch aus persönlicher Erfahrung kenne ich das Problem der Renormierbarkeit: Zu meiner Promotionszeit gab es einen Probevortrag zu einer Doktorarbeit, die eigentlich schon fast fertig zu sein schien. In der Fragestunde wies dann einer der anwesenden Professoren darauf hin, dass die Theorie – entgegen dem ersten Anschein – nicht ohne weiteres renormierbar sein dürfte, was die Bearbeitungszeit der Doktorarbeit dann nicht unbeträchtlich verlängerte.

So langsam wird der Weg unseres Teilchens von A nach B wirklich ziemlich kompliziert, oder? Nicht nur, dass wir alle Möglichkeiten betrachten müssen, wie das Teilchen fliuegen kann, jetzt kann es unterwegs auch noch “virtuelle Teilchen” aussenden und wieder einfangen und das, was wir experimentell für die Eigenschaften unseres Teilchens (wie Masse oder Ladung) halten, ist gar nicht das, was das Teilchen “wirklich” an Eigenschaften hat. Und dabei habe ich bisher nur ein einfaches Elektron angeguckt, das auch nur Photonen aussenden konnte. In Wahrheit gibt es aber ja auch noch andere Teilchen in der Welt, die das ganze noch weiter verkomplizieren. Das tun sie dann aber erst im nächsten Teil.

Zum Abschluss ein kleiner Warnhinweis: Ich habe bei der Darstellung der Renormierung einiges stark vereinfacht und viele Komplikationen komplett weggelassen (beispielsweise kann man sich fragen, was passiert, wenn das Elektron zwei Photonen nacheinander aussendet und dann wieder einfängt – das gibt zusätzliche Beiträge zur Renormierung, die man auch berücksichtigen muss). So ganz tief ist mein eigenes Verständnis der Renormierung auch nicht – obwohl ich denke, dass ich die Grundidee richtig wiedergegeben habe, übernehme ich keine Garantie, dass ich nicht irgendwo begrifflich oder sonstwie etwas geschlampt habe.

Lesetipp: Eine konzeptionell sehr klare (und zudem ziemlich lustige) Darstellung (in Dialogform!) der Renormierung findet ihr im Buch “Quantum Field Theory in a Nutshell” von Zee, Kapitel III.1.