Der Nachweis der kosmischen Inflation durch die Entdeckung von Gravitationswellen (bzw. deren Spuren) ist ja schon eine Weile her und wurde von Florian ausführlich erklärt (klickt den Link oben…). [NACHTRAG: Inzwischen wissen wir, dass die Messung fehlerhaft war, Gravitationswellen wurden aber ja jetzt auf andere Weise nachgewiesen.] Da mein Blog – besonders im Moment – nicht so der tagesaktuelle ist, schreibe ich nicht noch mehr darüber, sondern tue das, was ich am liebsten tue: Ich werfe einen Blick auf die physikalischen Prinzipien, die dahinter stehen. Und da stellt sich natürlich die Frage: Was sind eigentlich Gravitationswellen? Irgendwie sollen die ja die Raumzeit verzerren – aber wie genau sieht das aus? Sind die so ähnlich wie elektromagnetische Wellen?
Um diese Frage zu klären werfen wir erst mal einen Blick auf Einsteins Allgemeine Relativitätstheorie. Die beruht auf zwei cleveren Ideen von Albert Einstein (und einer Menge Mathematik dahinter, bis man diese Ideen sinnvoll zusammenbringt, aber auf die Mathematik verzichte ich heute….).
Einsteins erste brillante Erkenntnis, die zur Allgemeinen Relativitätstheorie (kurz: ART) führte, war, dass man die Gravitation als einen geometrischen Effekt “wegerklären” kann – es gibt in Wahrheit gar keine Gravitationsfelder, sondern es gibt stattdessen eine gekrümmte Raumzeit. In dieser sind Teilchen, auf die keine weiteren Kräfte wirken, im freien Fall – aber weil die Raumzeit gekrümmt ist, folgen sie nicht einfach geraden Bahnen, sondern eben Bahnen, die gekrümmt sind, so wie zum Beispiel ein Ball, den man wirft, eine Parabel beschreibt. (Wenn man genau ist, sind diese Bahnen nicht gekrümmt, sondern sind “so gerade wie möglich” – so genannte Geodäten – aber das erkläre ich hier nicht. Über solche Details der Raumzeitkrümmung brauchen wir uns hier erst mal keine Gedanken zu machen – wer mehr wissen will, findet rechts bei den “Artikelserien” eine 6-teilige Monsterserie über die Raumzeitkrümmung.)
Leider können wir den “Raum” nicht direkt beobachten – Raum kann man nicht anfassen (und Zeit auch nicht). Beobachten können wir Objekte im Raum (und der Zeit) – wenn wir also verstehen wollen, wie Gravitationswellen die Raumzeit beeinflussen, dann müssen wir uns Objekte in der Raumzeit angucken.
Das ist übrigens ähnlich mit elektrischen Feldern (die Analogie zu elektrischen Feldern werde ich im folgenden immer wieder verwenden): Elektrische Felder üben eine Kraft auf elektrische Ladungen aus – und die ist das, was wir beobachten. Eine Radiowelle bringt zum Beispiel Elektronen in der Antenne eures Radiogeräts zum Schwingen (es sei denn, ihr hört Radio übers Internet…), und diese Schwingung wird dann verstärkt und in Schallsignale umgewandelt. (Einstein hat übrigens die letzten 30 Jahre seines Lebens zu einem Großteil damit verbracht, zu versuchen, seinen Erfolg für die Gravitation auch für die Theorie des Elektromagnetismus zu wiederholen – aber den Elektromagnetismus kann man nicht direkt auf die Geometrie der Raumzeit zurückführen. (Obwohl unsere aktuelle Theorie des Elektromagnetismus – die Quantenelektrodynamik – als so genannte Eichtheorie in vieler Hinsicht sehr ähnlich zur ART ist.))
Wenn wir also elektromagnetische Wellen untersuchen wollen, müssen wir uns ein Teilchen angucken, das elektrisch geladen ist, und dann sehen, was die elektromagnetische Welle mit dem Teilchen macht. Dabei stellen wir fest, dass unser Teilchen sich im elektrischen Feld der em-Welle bewegt – es oszilliert, bewegt sich also periodisch hin und her und wird dabei beschleunigt.
Man könnte also – ganz analog – annehmen, dass man ein Teilchen mit einer “gravitativen Ladung ” betrachten muss, um Gravitationswellen zu finden. Da Schwerefelder von Massen erzeugt werden (oder, anders gesagt, da Massen die Raumzeit krümmen), ist eine Masse nichts anderes als eine Gravitationsladung. Können wir also am Verhalten einer einzelnen Masse sehen, wie eine Gravitationswelle wirkt?
Nein, das können wir nicht. Einsteins zweite brillante Erkenntnis war das sogenannte Äquivalenzprinzip – das besagt gerade, das Teilchen, auf die nur “Schwerefelder” wirken, von diesen nichts merken und im freien Fall sind. Wenn ihr im Weltall auf der ISS herumturnt, seid ihr im freien Fall und damit schwerelos; ebenso wenn ihr in einem Flugzeug auf einer Parabelbahn fliegt oder (näherungsweise) wenn es in der Achterbahn vorm Looping rapide nach unten geht. Würde man euch die Augen verbinden, könntet ihr nicht sagen, ob ihr gerade mutterseelenallein im Weltall schwebt (o.k., dazu bräuchtet ihr vielleicht noch nen Raumanzug…) oder ob ihr gerade im freien Fall auf die Erde zustürzt.
Fazit: Anders als bei einer em-Welle kann ein einsames Punktteilchen von einer Gravitationswelle nichts bemerken, weil es die ganze Zeit im freien Fall ist.
Um die Wirkung einer Gravitationswelle zu verstehen, muss man also mehrere Teilchen betrachten und sehen, was diese Teilchen tun.
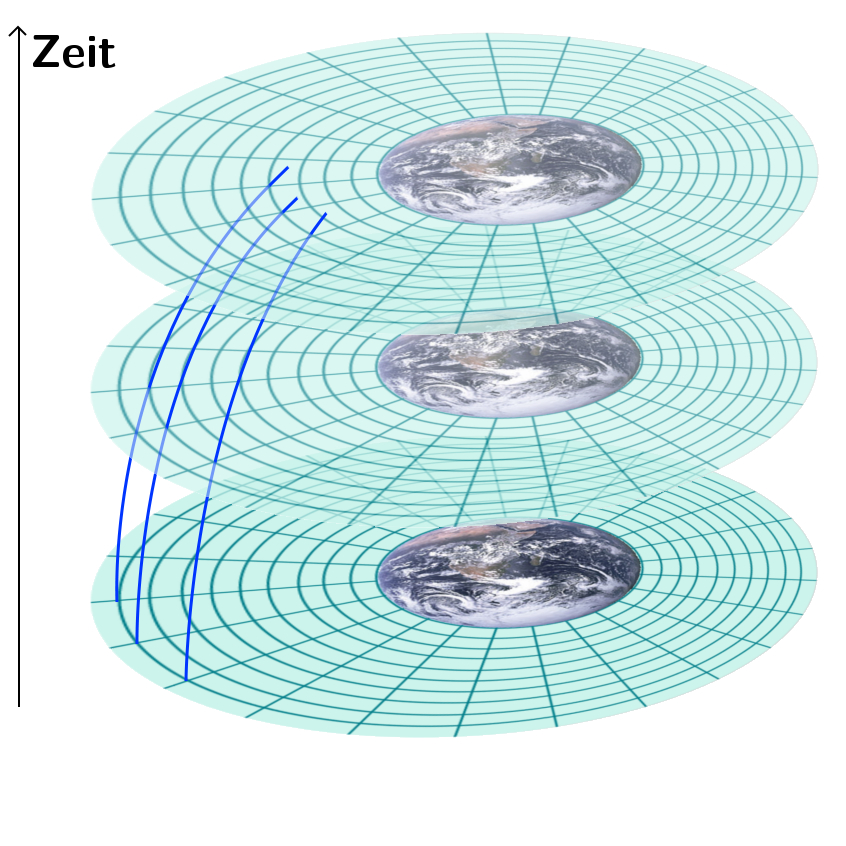
Betrachten wir erst mal drei Teilchen in der Nähe der Erde (die nachfolgenden Bilder stammen aus der Raumzeit-Krümmungs-Serie). Wir lassen sie in gleicher Entfernung nebeneinander starten und gucken, was passiert (hier ist in Richtung nach oben die zeit aufgetragen, die Erde habe ich dafür auf zwei Dimensionen plattgebügelt):
Wie ihr seht, laufen die Teilchen aufeinander zu – sie fallen alle in Richtung Erdmittelpunkt, ihr Abstand wird also kleiner. Die Linien starten senkrecht (am Anfang sind die Teilchen in Ruhe) und kippen dann immer weiter nach rechts ab, weil die Teilchen beim Fallen immer schneller werden.
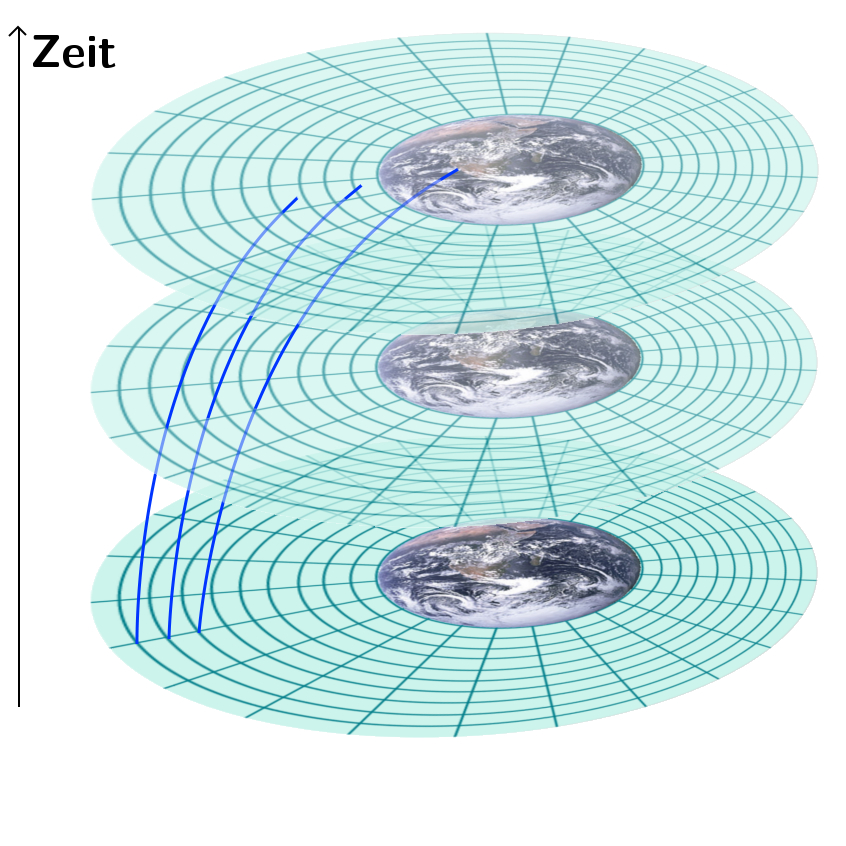
Lassen wir die drei Teilchen als nächstes in unterschiedlichem Abstand starten:
Das Teilchen, das dichter an der Erde dran ist, wird stärker angezogen (in der Sprache der Schwerefelder) und wird deswegen stärker beschleunigt. Die Teilchen entfernen sich also voneinander.
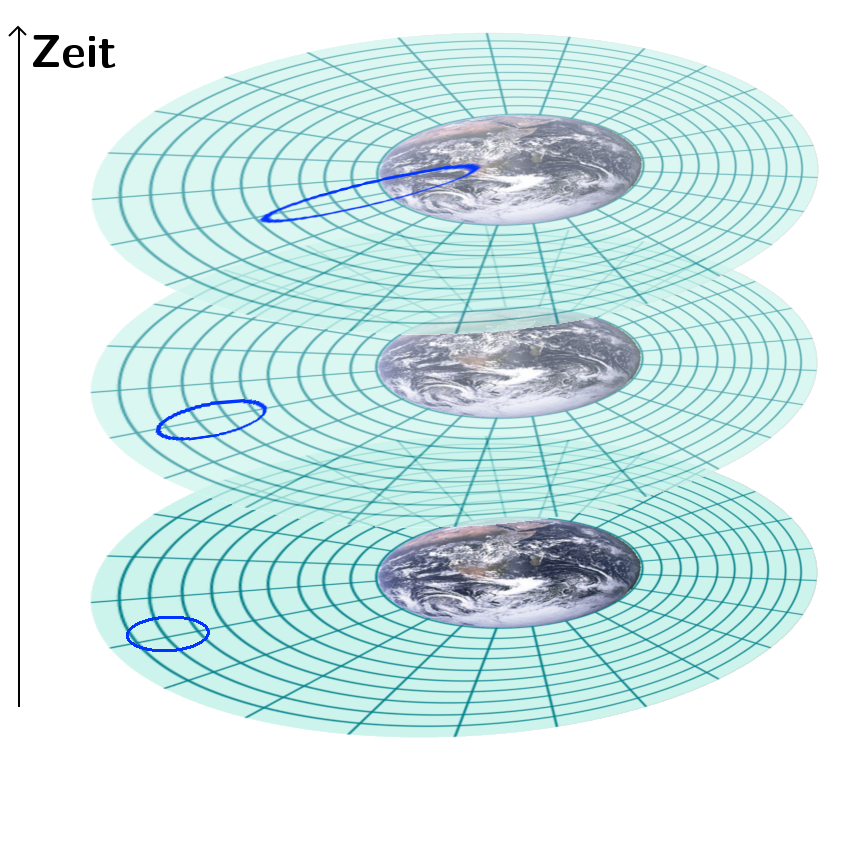
Wir können beide Bilder zusammenfassen, wenn wir zeichnen, was mit einem Ring aus Teilchen passiert:
Ein solcher Ring wird also verzerrt. Wenn man alles ganz sauber ausrechnet und aufzeichnet, dann sieht man, dass aus dem Ring eine Ellipse wird, wobei sich aber die Fläche nicht ändert.
Anders sähe die Sache aus, wenn wir den Teilchenring im Inneren der Erde loslassen würden (wir stellen uns vor, dass die Materie der Erde die Teilchen nicht weiter stört). Je dichter wir am Erdmittelpunkt sind, desto schwächer ist die Schwerkraft, also fallen weiter außen liegende Teilchen schneller. Nach wie vor fallen die Teilchen, die nebeneinander starten, aufeinander zu. Insgesamt wird dadurch der anfängliche Kreis kleiner, er wird also als ganzes gestaucht.
Das ist nicht nur hier so, sondern eine ganz allgemeine Regel für den Einfluss der Raumzeitkrümmung auf einen Teilchenring: Wird durch den Ring Materie eingeschlossen, dann wird er zusammengezogen und ändert seine Fläche – ein Ring im Vakuum kann durch die Raumzeitkrümmung (also durch Schwerefelder) zwar verzerrt werden, aber seine Fläche nicht ändern. Nachtrag: Nach längerem Überlegen bin ich (Dank an Niels et al.) zu dem Schluss gekommen, dass diese Aussage so nicht haltbar ist (siehe die Diskussion unten): Wenn ich es richtig sehe, gilt das Argument aber für eine Kugel aus Teilchen – eine Kugel aus Teilchen ändert – zumindest anfänglich – ihr Volumen nicht, wenn keine Materie eingeschlossen ist. (Wen sie sich dann erst mal verzerrt hat, dann kann sie auch ihr Volumen ändern.) Für einen Ring gilt das nur, wenn senkrecht zur Ebene des Rings nichts passiert wie bei einer Gravitationswelle, da hatte ich etwas zu schnell verallgemeinert. Siehe auch unten meinen Kommentar #17. (Mehr zum Überschussradius findet ihr im zweiten Teil der Serie – dort erkläre ich, warum der Sonnenradius “zu groß” ist.)
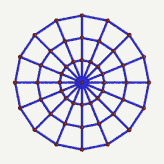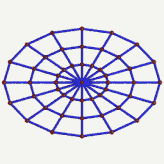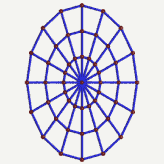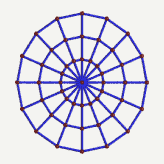
Zurück zu den Gravitationswellen. Um zu sehen, wie Gravitationswellen wirken, müssen wir uns also einen Ring aus Teilchen (oder eine andere Anordnung, aber ein Ring ist recht praktisch) im Vakuum angucken und Gravitationswellen draufschicken. (Die Frage, wo diese Wellen herkommen, klären wir später…) Hier ist unser Ring:
Wir stellen uns also einen Ring aus Teilchen vor, auf den eine Gravitationswelle trifft. (Man könnte auch eine Kugel nehmen, aber der Ring reicht, wie wir gleich sehen werden.) Die Welle trifft dabei senkrecht auf den Ring (stellt euch vor, eure Augen würden Gravitationswellen auf den Bildschirm strahlen), weil das am Einfachsten ist. Was kann so eine Welle mit dem Ring machen?
Dazu überlegen wir uns alle Möglichkeiten (ich hoffe, ich vergesse keine), wie sich so ein Ring verformen kann.
Zunächst mal könnte er als ganzes größer oder kleiner werden, so dass der Durchmesser des Kreises oszilliert, er aber seine Form nicht ändert, etwa so (nach rechts ist hier die Zeit aufgetragen, wir gucken von Vorn auf den Ring, genau in der Richtung, in der auch die Welle auf den Ring trifft):
Das geht aber – wie eben schon erwähnt – im Vakuum nicht. Die einzige Möglichkeit, wie man es erreichen könnte, wäre, wenn man eine Masse “aus dem Nichts” entstehen lässt, dann würde sich eine Stoßwelle durch die Raumzeit ausbreiten, die unseren Ring als Ganzes stauchen oder (wenn die Masse verschwindet) dehnen könnte. Da nach Einstein aber E=mc² ist und da die Energie erhalten ist, geht das so nicht: Um Energie irgendwohin zu bekommen, muss man sie dorthin transportieren, man kann sie nicht einfach entstehen lassen. (Etwas Ähnliches gilt übrigens – wegen der Erhaltung der elektrischen Ladung – auch für elektrische Felder. Eine plötzlich entstehende elektrische Ladung würde eine elektrische Longitudinalwelle als Stoßwelle erzeugen, also eine, bei der das elektrische Feld in Ausbreitungsrichtung zeigt. Solche Wellen gibt es aber nicht.)
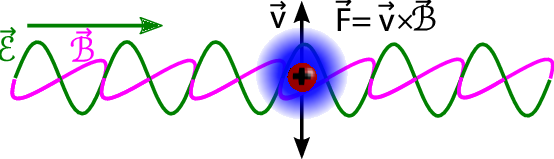
Die nächste Möglichkeit – und eine, die erst mal ganz plausibel aussieht – wäre die, dass wir unseren Ring zum Auf- und Abschwingen bringen. So wäre es ja mit einer elektromagnetischen Welle wie in diesem Bild hier (geklaut aus meinem demnächst erscheinenden Buch…):
Von links kommt eine em-Welle (elektrische Felder sind grün, Magnetfelder magenta) und bringt die elektrische Ladung in der Mitte zum Auf- und Abschwingen. Zusätzlich entsteht noch eine Kraft nach rechts, weil die bewegte Ladung eine Geschwindigkeit hat und das Magnetfeld darauf eine Kraft ausübt (das ist auch die Formel im Bild) – aber dieser Effekt ist klein und für uns nicht relevant (es ist der berühmte Lichtdruck).
Ein Ring aus elektrischen Ladungen würde also ebenfalls auf- und ab-schwingen. Kann ein Ring aus Massen in einer Gravitationswelle auch in dieser Weise auf- und abschwingen?
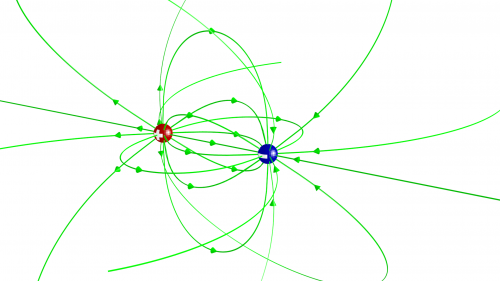
Dazu müssen wir uns fragen, wieso denn eigentlich das elektrische Feld in der em-Welle auf- und abschwingt. Eine em-Welle könnt ihr ja mit einer Antenne erzeugen, in der Elektronen mit ihrer elektrischen Ladung auf und ab beschleunigt werden und oszillieren. Weil so eine Antenne etwas unübersichtlich ist (es gibt viele Elektronen drin und positive Atomkerne, die die Gesamtladung ausgleichen), nehmen wir stattdessen den einfachsten Fall: Wir denken uns eine positive und eine negative Ladung gleicher Stärke, einen sogenannten Dipol. Die haben ein elektrisches Feld, das etwa so aussieht:
Die Feldlinien zeigen dabei von der positiven zur negativen Ladung. Um mit einem solchen Dipol eine em-Welle zu erzeugen, können wir die beiden Ladungen zum Beispiel mit einer (ungeladenen) Feder verbinden und dann schwingen lassen. Weil die beiden Ladungen entlang einer Achse schwingen, entsteht ein passend dazu gerichtetes elektrisches Feld (jedenfalls, wenn man senkrecht zur Verbindungslinie nach außen guckt), das ebenfalls schwingt, also unsere em-Welle. Deswegen heißt eine solche Welle auch Dipol-Welle. (Mathematisch ist unser Dipol-Moment der Abstand zwischen den Ladungen multipliziert mit der Ladungsstärke. Die Stärke der entstehenden Welle ist dann proportional zur Ladungsstärke mal der Beschleunigung, also der zweiten Ableitung des Abstands nach der Zeit.)
Versuchen wir dasselbe mit Massen. Wir verbinden also zwei Massen mit einer Feder und lassen sie schwingen. Bekommen wir eine Gravitationswelle?
Leider nein. Beim elektrischen Dipol hatten die beiden Ladungen ja entgegengesetztes Vorzeichen – eine war positiv und eine negativ. Beim Massen-Dipol ist das anders: Massen gibt es nur mit einem Vorzeichen (es gibt keine “Anti-Masse”). Betrachtet man jetzt den Effekt der Schwingung, dann hebt die Bewegung der einen Masse genau die der anderen Masse auf. (Der Grund dafür ist das 3. Newtonsche Axiom: Auch beim Massendipol ist die Stärke gleich der zweiten Ableitung nach der Zeit, aber die Summe über alle Beschleunigungen im System ist wegen F=ma und “actio=reactio” immer gleich Null.) Nachtrag: Dieser Absatz ist nicht ganz richtig. Wir bekommen tatsächlich keine Gravitationswelle durch ein Dipolmoment – das verschwindet, insofern ist die Erklärung richtig. Aber die schwingenden Massen haben ein “Quadrupolmoment” (klingt komisch, weil es ja zwei sind, nicht vier, ist aber so) und senden deshalb trotzdem Gravitationswellen aus. Das, worum es mir ging (Gravitationswellen haben keinen Dipol-Charakter) ist also richtig, aber dass die schwingenden massen gar keine Wellen aussenden, ist falsch. Dank an Markus Pössel, der es mir geduldig erklärt hat.
Eine Gravitationswelle kommt also nicht durch einen Massendipol zu Stande. Entsprechend können wir unseren Ring nicht als ganzes nach oben oder unten verschieben.
Das nächst-kompliziertere Verformungsmuster für unseren Ring ist, ihn in eine Ellipse mit gleicher Fläche zu verzerren. (Die Fläche darf sich ja nicht ändern, wie wir oben gesehen haben – ich gebe aber zu, dass ich beim Zeichnen nicht ganz exakt war…).
Der Ring oszilliert also jeweils zwischen zwei Ellipsenformen, zwischendurch ist er aber immer auch mal unverformt. Auf der schönen Seite Einstein online (generell eine gute Adresse, wenn es um die Relativitätstheorie geht) gibt es dazu auch eine schicke Animation (Dank an Markus Pössel):
Breitet sich so eine Verzerrung aus, dann sieht das etwa so aus:
Natürlich kann die Ellipse auch gedreht sein, etwa so:
Die einzelnen Teilchen bewegen sich dabei nur wenig.
Diese beiden um 45° zueinander gedrehten Möglichkeiten reichen schon, um alle denkbaren Orientierungen der Ellipsen zu bekommen; wenn ihr einen anderen Winkel wollt, dann könnt ihr die beiden Ellipsen passend überlagern. (Das ist ganz analog zu einer em-Welle – auch dort gibt es zwei Möglichkeiten für das elektrische Feld: Es kann entweder senkrecht oder waagerecht schwingen, andere Orientierungen bekommt ihr ebenfalls durch Überlagerung.) Wellen dieser Art nennt man auch Quadrupol-Wellen.
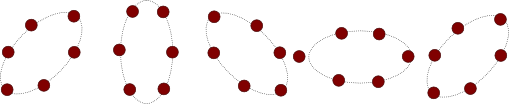
Man kann die beiden Ellipsen aber auch zeitversetzt überlagern, dann bekommt man so ein Muster:
Dieses Bild kann man leicht falsch verstehen: Die einzelnen Teilchen rotieren nicht mit dem Ring, sondern beschreiben nur kleine Kreisbahnen um ihre Position herum.
Auch hier gibt es wieder zwei Möglichkeiten – die Ellipse kann sich links- oder rechtsrum drehen. Wichtig ist dabei, dass die einzelnen Teilchen des Rings nicht um den ganzen Ring herumrotieren, sondern alle nur kleine Bewegungen um ihre Ruhelage machen. Auch die rotierende Ellipse ist wieder ganz analog zur em-Welle: Auch dort kann man durch zeitlich verschobene Überlagerung eine sogenannte zirkular polarisierte Welle bekommen, die sieht so aus:
Auch diese Welle kann sich entweder mit dem oder gegen den Uhrzeigersinn drehen.
Die Orientierung der Welle bezeichnet man generell als ihre Polarisation. Dass es letztlich nur zwei Möglichkeiten für diese Polarisation gibt, hängt damit zusammen, dass die Welle sich mit Lichtgeschwindigkeit ausbreitet und dass ihr sie deshalb nicht überholen könnt. Bei der Lichtwelle bekommt ihr übrigens in allen Fällen eine identisch aussehende Welle, wenn ihr das Bild um 360° dreht; bei der Gravitationswelle schon, wenn ihr es um 180° dreht. (Wenn ihr den Sprung zur Quantentheorie macht, ist das genau der Grund, warum Photonen einen Spin von 1 haben müssen und Gravitonen einen von 2. Mehr zum Thema Teilchenspin findet ihr hier und hier. Und da man auch Gravitonen nicht überholen kann, haben die auch nur zwei mögliche Zustände des Spins; Spin-2-Teilchen mit Masse hätten 5 Möglichkeiten. Hmmm, über Gravitonen habe ich noch nie geschrieben, aber das werde ich hoffentlich bald mal nachholen, dann verstehe ich die Dinger vielleicht mal….)
Dass ich so detailliert auf dieses Verformungsmuster unseres Rings eingehe, lässt schon ahnen, dass das jetzt tatsächlich mal eine Verformung ist, die mit Gravitationswellen auch möglich ist – und so ist es auch. Dazu dürfen die Massen nicht bloß gegeneinander schwingen, sondern müssen umeinander herum rotieren, etwa so:

By User:Zhatt – Own work, Public Domain, Link
Dabei entstehen dann Gravitationswellen; das veranschaulicht diese Animation der NASA (zwei oszillierende Neutronensterne sitzen in der Mitte und strahlen die Wellen nach Außen ab):

By NASA/JPL – https://lisa.jpl.nasa.gov/popups/ripples.html
https://lisa.jpl.nasa.gov/IMAGES/wavy.gif, Public Domain, Link
Eine sehr schöne Animation (auf allerdings augenentzündungenverursachendem (ein Wort von geradezu Homerscher Länge…) Hintergrund) findet ihr auch auf dieser Seite.
Auch in unserem Sonnensystem entstehen solche Wellen, weil die Planeten um die Sonne kreisen. Allerdings sind sie unglaublich schwach – Das System Sonne-Jupiter beispielsweise strahlt etwa 40Watt an Gravitations-Energie nach außen ab (die Strahlungsleistung der Sonne beträgt etwa 4E26Watt, also 100 Billionen Billionen Mal so viel – kein Wunder, dass wir Sterne leicht sehen können, aber nicht so viel von ihren Gravitationswellen bemerken…).
Welche Möglichkeiten gäbe es noch für unseren Ring? Er könnte sich theoretisch auch entlang der Ausbreitung der Welle verschieben – aber genau wie bei den em-Wellen wäre das eine Longitudinalwelle, die es nicht geben kann (dazu müsste man die Energieerhaltung verletzen).
Außerdem könnte man ja noch auf die Idee kommen, dass sich nach Einstein ja nicht bloß der Raum krümmt, sondern die Raumzeit – beeinflusst eine Gravitationswelle vielleicht auch den Zeitverlauf unserer Teilchen, so dass bei ihnen die Zeit mal schneller und mal langsamer vergeht? Auch das kann – letztlich aus demselben Grund der Energieerhaltung – nicht passieren.
Theoretisch sind auch kompliziertere Schwingungsmuster als die einfache Ellipsenverzerrung möglich – die bezeichnet man dann z.B. als Oktopol- oder generell als Multipol-Wellen. Solche Wellen zu erzeugen erfordert aber entsprechend kompliziertere Anordnungen der Massen, deshalb sind sie nicht ganz so wichtig.
Gravitationswellen führen also zu elliptischen Verzerrungen. Es sind genau diese Verzerrungen, die zu dem charakteristischen Muster der “B-Moden” führen, das man in der kosmischen Mikrowellenstrahlung entdeckt hat. Eine – stellenweise anspruchsvolle, aber schön illustrierte – Erklärung dazu findet ihr an der Uni Berkeley; in dem Bild in Abschnitt 5 findet ihr auch genau die verzerrten Ellipsen wieder, die zeigen, wie Gravitationswellen den Raum krümmen.
Wieder einmal ist ein kurzer Text zum Thema viel länger geworden als erwartet – und es gäbe noch viel mehr zu schreiben (insbesondere über das Thema Gravitonen…). Ich hoffe, ihr habt aber zumindest eine kleine Idee bekommen, was Gravitationswellen sind.












Kommentare (50)