Das Wort “Nullpunktsenergie” geistert ja öfters mal herum – es ist eine Energie, die da ist, wenn eigentlich nichts da ist (nämlich im Vakuum), und manche Leute wollen sie sogar anzapfen und damit alle Energieprobleme der Welt lösen (das klappt aber nur in der science fiction). Das Konzept der Nullpunktsenergie stammt aber nicht aus der Theorie des Vakuums (oder der Elementarteilchen), sondern aus der Quantenmechanik von Atomen und Molekülen. Und zumindest dort hat diese Nullpunktsenergie auch ganz deutliche und messbare Konsequenzen.
Stellt euch ein einfaches Molekül vor, das aus zwei Atomen besteht, zum Beispiel ein Wasserstoff-Molekül. Das besteht ja aus zwei Wasserstoffatomen, die chemisch aneinander gebunden sind. Der Abstand zwischen den beiden Atomen in unserem Molekül ist durch die Kraft bestimmt: zum einen ziehen sie sich an, zum anderen möchten sie sich auch nicht zu nahe kommen, weil die Elektronen sich am liebsten über einen Bereich verteilen wollen (und weil die positiv geladenen Atomkerne sich abstoßen). (Relativ ausführlich habe ich das als Beispiel mal in der Quantenmechanik-verstehen-Serie besprochen.) Schiebt man die beiden Atome also dichter zusammen, dann stoßen sie sich ab, zieht man sie auseinander, dann ziehen sie sich an.
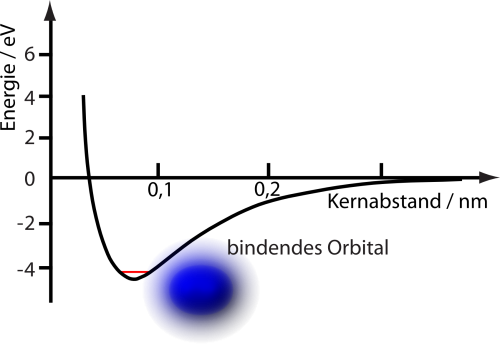
Zeichnet man die Energie als Funktion des Abstands, sieht das Bild etwa so aus:
Dabei habe ich in blau die Verteilung der Elektronenwolken (das Orbital) im Molekül eingezeichnet. Ihr seht, dass es einen Abstand gibt, bei dem die Energie minimal wird, das ist entsprechend der Gleichgewichtsabstand der Moleküle.
Wir können uns das – als brauchbare Analogie – so vorstellen, als wären die beiden Atome mit einer kleinen Feder verbunden, die gerade die passende Gleichgewichts-Länge hat. (Das ist natürlich nur eine Veranschaulichung, sooo kleine Federn gibt es nicht- die müssten dann ja auch aus Sub-Atomen bestehen, die sich anziehen, wofür wir dann Sub-Sub-Atome bräuchten usw….)
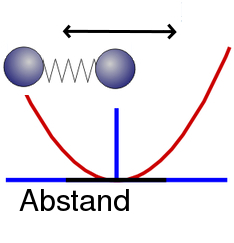
Im einfachsten Fall ist die rückstellende Kraft bei so einer Feder genau proportional zur Auslenkung: Je weiter ihr die Feder dehnt (oder staucht), desto größer wird sie. Schaut man sich die Energie an, die man reinstecken muss, um die Feder zu dehnen (oder zu stauchen, ich schreibe das jetzt nicht jedesmal mit hin…), so ist diese proportional zum Quadrat der Auslenkung, denn es gilt ja: Arbeit ist Kraft mal Weg, und wenn die Kraft porportional zum Weg ist, dann ist die Arbeit proportional zum Quadrat des Weges. Trägt man also die Energie auf, dann sieht das so aus:
Der blaue Strich kennzeichnet die Gleichgewichtslage, da wo die Atome in Ruhe sind und ihren energetisch günstigsten Abstand haben, die rote Linie zeigt, wie sich die Energie mit zunehmender Auslenkung ändert. Wenn ihr das Bild mit dem Bild für die Energie des Wasserstoffmoleküls oben vergleicht, dann seht ihr, dass die rote Parabel in der Nähe des Minimums eine ganz brauchbare Näherung darstellt. (Was mathematisch nicht verwunderlich ist, weil man so ziemlich jede Funktion in der Nähe des Minimums mit einer Parabel annähern kann.)
Wir haben also – in unserem einfachen Modell – zwei Objekte, die mit einer Feder verbunden sind. Wenn man die beiden Atome etwas auseinander zieht und dann loslässt, dann werden sie anfangen zu schwingen, jedenfalls nach den Regeln der klassischen Physik. Die Schwingung hat dabei eine bestimmte Frequenz (die Eigenfrequenz oder auch Resonanzfrequenz), die also sagt, wie lange eine Schwingung dauert. Solange die Auslenkung der Atome einigermaßen klein ist, ist die Frequenz unabhängig von der Auslenkung, und ihr könnt – immer noch im Rahmen der klassischen Physik – beliebige Auslenkungen bekommen. Die zugehörige Energie ist dadurch bestimmt, wie weit die beiden Atome maximal auseinander sind – auch sie kann entsprechend beliebige Werte annehmen.
Wir betrachten jetzt dieses System (zwei verbundene schwingende Atome, bei denen die Kraft dem einfachen Gesetz Kraft proportional zur Auslenkung folgt) mit den Regeln der Quantenmechanik. Die ganze Rechnerei überlassen wir den armen Physik-Studis, die hier ihre Fähigkeiten im Lösen partieller Differentialgleichungen üben können, hier geht es nur um das, was dabei herauskommt. (Ein didaktisches Problem in der Physik ist genau diese Trennung: In Physikvorlesungen und Büchern wird immer beides parallel gemacht: das Lösen fieser Gleichungen und ähnliches rein mathematisches Zeugs und das physikalische Argumentieren und Interpretieren vermischen sich da oft zu einem wirren und verwirrenden Brei, jedenfalls ging es mir und vielen meiner KommilitonInnen seinerzeit so.)
Zunächst einmal gilt in der Quantenmechanik die (etwas seltsam anmutende) Regel, dass es einerseits Zustände mit genau definierter Energie gibt und andererseits solche, bei denen die Energie nicht “scharf” definiert ist. (Mehr über Zustände in der Quantenmechanik erfahrt ihr in dieser Serie.) Zustände, bei denen die Energie einen eindeutigen, genauen Wert hat, sind gleichzeitig auch stationär, sie hängen also nicht von der Zeit ab. (Für PedantInnen: Ja, bis auf einen Phasenfaktor…) Da wir uns hier für die Energien interessieren, betrachten wir nur Zustände, deren Energie eindeutig ist.
Dabei ist die Energie eines solchen Systems aus zwei Atomen nicht mehr beliebig, sondern quantisiert (deswegen heißt es ja auch Quantenmechanik) – sie kann also nur ganz bestimmte Werte annehmen. Ihr könnt also keine beliebigen Schwingungsenergien mehr bekommen (so wie in der klassischen Physik), sondern nur ganz bestimmte. Bezeichnet ihr die Schwingfrequenz mit dem Buchstaben ν (griechisch “nu”, nicht “vau”), dann gilt die Regel, dass ihr dem System Schwingungsenergie nur in Paketen der Größe hν (oder Vielfachen davon) zuführen könnt; h ist dabei das Plancksche Wirkungsquantum.
Wenn das System also ein bisschen schwingt, dann könnt ihr es – anders als in der klassischen Physik – nicht ein ganz winzig kleines bisschen mehr schwingen lassen, sondern eben nur die Energie um mindestens hν erhöhen. (Sehr ausführlich habe ich dieses System auch in meiner QFT-Serie besprochen.) Planck hat diese Idee der Quantisierung von Molekülschwingungen übrigens eingeführt, um damit das Lichtspektrum von erhitzten Körpern zu erklären. Für ihn war das allerdings nur ein reines ad-hoc-Modell (die Quantenmechanik gab es damals noch nicht, die fing erst mit dieser Idee an), denn zu dieser Zeit glaubte er eigentlich noch nicht, dass die Materie aus Atomen aufgebaut ist, sondern nahm an, sie sei kontinuierlich.
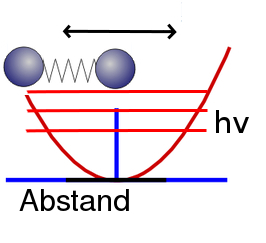
Zeichnet man ein paar der Energieniveaus in das Bild ein, dann sieht das etwa so aus (das hν kennzeichnet den Abstand zweier Niveaus):
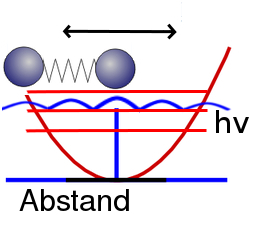
Hat unser schwingendes Molekül eine bestimmte Schwingungsenergie (wobei eben nicht jede beliebige Energie möglich ist, sondern nur ganz bestimmte Energien), dann gehört dazu eine Wahrscheinlichkeitsverteilung: Der Abstand zwischen den Molekülen ist nicht eindeutig definiert, stattdessen gibt es eine Wahrscheinlichkeit dafür, einen bestimmten Abstand zu messen. Weil zu großen Abständen der Moleküle große Energien gehören, ist die Wahrscheinlichkeit, einen großen Abstand zu messen, groß, wenn die Energie groß ist, und klein, wenn die Energie klein ist. Umgekehrt findet ihr bei kleiner Energie die beiden Moleküle eher etwa im Gleichgewichtsabstand. (Ich erkläre das hier nur sehr grob, Details könnt ihr auch in meiner Serie zur Schrödingergleichung (siehe die Artikelserien) nachlesen, allerdings nicht für ein schwingendes Molekül, die Logik ist aber immer dieselbe.) Hier habe ich das – ziemlich grob und schematisch – für eins der Energieniveaus in blau eingezeichnet:
(Dass die Wahrscheinlichkeit für die Abstände nicht einfach nach Außen hin abfällt, sondern dass es immer Maxima und Minima gibt, ist ganz normal und hat etwas mit dem Wellencharakter der Materie zu tun. Ihr braucht euch darüber hier aber keine Gedanken zu machen, denn für das Thema Nullpunktsenergie spielt das keine große Rolle.)
Je niedriger die Energie unseres schwingenden Moleküls ist, desto wahrscheinlicher ist es also, dass wir als Abstand der beiden Moleküle in etwa den Gleichgewichtsabstand finden.Wenn wir die Energie also immer weiter verkleinern, dann sollten wir die beiden Atome mit immer höherer Wahrscheinlichkeit im Gleichgewichtsabstand finden.
(Anmerkung für die ganz Genauen: Ich schreibe hier extra “in etwa”, weil bei ungeraden Quantenzahlen die Wahrscheinlichkeit des Gleichgewichtsabstandes verschwindet, die Wellenfunktion hat hier einen Knoten)
Und was ist, wenn wir die Energie so niedrig machen, wie es überhaupt nur geht? Wenn wir also dem schwingenden Molekül seine Schwingungsenergie vollkommen entziehen – soweit das eben möglich ist? Dann sollte es logischerweise Energie Null haben (wobei der Energienullpunkt durch das Minimum der Energiekurve oben definiert ist). Die beiden Atome wären dann genau im Gleichgewichtsabstand.
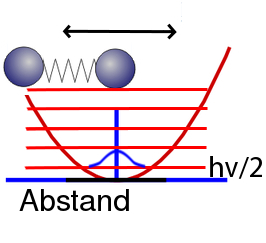
Das scheint ganz plausibel, ist aber falsch: Der Zustand mit der niedrigsten Energie hat eine höhere Energie als das Minimum unserer Kurve. Sie beträgt hν/2. Während ihr einem klassischen System alle Schwingungsenergie entziehen könnt, ist das bei einem quantenmechanischen Schwinger nicht möglich, da bleibt immer etwas Schwingungsenergie übrig. So etwa sehen die Energieniveaus aus:
In blau habe ich wieder die Wahrscheinlichkeit aufgetragen, allerdings nicht ganz maßstabsgetreu.
Man kann sich diese Wahrscheinlichkeitsverteilung auch über die berühmte Unschärfe-Relation erklären: Wenn die beiden Atome genau den Gleichgewichtsabstand haben, dann kennen wir ihren Ort perfekt genau (jedenfalls relativ zueinander) – ebenso aber ihre Geschwindigkeit, weil die beiden ja in Ruhe sind. Das ist aber nicht möglich.
Die Energie ist also in unserem quantenmechanischen Schwinger nie ganz so niedrig, wie sie es in der klassischen Physik sein könnte, sondern etwas größer. Das ist die berühmte Nullpunktsenergie, die Energie, die auch dann da ist, wenn wir unser System auf den absoluten Nullpunkt abkühlen, so dass es alle Energie abgegeben hat, die es abgeben kann.
Ist diese Nullpunktsenergie für irgendetwas relevant? Wenn ich sie dem System nicht entziehen kann, dann kann ich ja immer nur Änderungen relativ zur Nullpunktsenergie betrachten – ich kann dem System Energie (in Paketen der Größe hν) zuführen oder wieder entziehen, aber an der Nullpunktsenergie ändert sich nichts. Ich kann im Zweifel ja einfach meinen Energie-Nullpunkt ein bisschen nach oben verschieben, und dann ist wieder alles gut. Insofern sollte die Nullpunktsenergie eines Moleküls eigentlich ziemlich irrelevant sein – sie ist sicherlich interessant, aber eher was für Theorie-Fans, oder?
Wenn ihr das denkt, dann seid ihr vermutlich in guter Gesellschaft – die meisten Physikbücher, die ich kenne, erwecken zumindest den Eindruck, dass die Nullpunktsenergie in solchen schwingenden Systemen nicht besonders wichtig ist, und ich selbst habe das auch bis vor kurzem gedacht.
Um zu sehen, warum die Nullpunktsenergie doch wichtig sein kann, stellt euch vor, ihr wolltet die Eigenschaften unseres Moleküls berechnen, also insbesondere auch seine Bindungsenergie. Was man dazu tun kann, ist, das Verhalten der Elektronen des Moleküls für verschiedene feste Abstände der beiden Atomkerne zu analysieren und die zugehörige Energie zu berechnen, so wie in dem Bild ganz oben. Das ist eine sinnvolle Methode, weil die Atomkerne ja verglichen mit den Elektronen sehr schwer sind – die Dynamik der Elektronen ist für die chemische Bindung eben viel wichtiger als die der Kerne. Daran könnt ihr jetzt die Energie des Moleküls ablesen, es ist logischerweise die Energie im Minimum.
Oder auch nicht. Denn die beiden Atomkerne könnten ja auch gegeneinander schwingen – und damit gibt es eine Nullpunktsenergie. Der tatsächliche Zustand niedrigster Energie liegt also etwas höher als das Minimum, das ihr gerade berechnet habt. Und das muss man berücksichtigen, wenn man zum Beispiel die Struktur von Molekülen oder chemische Reaktionen anguckt. Für das Wasserstoffmolekül beträgt die Energieänderung durch die Nullpunktsenergie etwa 0,27 Elektronenvolt (wenn ich die Zahlen auf dieser Seite richtig verwendet habe; das Elektronenvolt ist einfach eine Energieeinheit, die in der Atomphysik praktisch ist, weil dann handliche Zahlenwerte herauskommen). Zeichnet man diese Energie in unser Bild von ganz oben ein, sieht das so aus (ehrlich gesagt, bin ich mir nicht 100% sicher, dass das Bild so stimmt – es mag sein, dass in der schwarzen Kurve die Nullpunktsenergie schon enthalten war; da ich momentan keinen Zugriff auf die Quelle habe, aus der die Kurve stammt, kann ich das nicht genau sagen):
Wenn ihr also zum Beispiel eine chemische Reaktion berechnet, bei der sich ein Wasserstoffmolekül bildet, dann dürft ihr eben nicht einfach die Energie im Minimum der Kurve verwenden, sondern müsst berücksichtigen, dass die tatsächliche Bindungsenergie etwas kleiner ist. (Das Energieniveau liegt etwas höher, die zugehörige Energie, die ich bekomme, wenn ich von einem Zustand mit Energie Null in dieses Niveau gehe, ist also kleiner.) Die Nullpunktsenergie hat also tatsächlich messbare Konsequenzen, wenn es sie nicht gäbe, würden sich die Bindungsenergien von Molekülen entsprechend ändern.
Direkt nachmessen können wir die Nullpunktsenergie natürlich nicht (wir können dem Molekül nicht seine Schwingungsmöglichkeit wegnehmen, so dass es dann das echte Minimum der Kurve erreicht), aber ohne die Nullpunktsenergie gäbe es eine Diskrepanz zwischen der berechneten und der tatsächlichen Bindungsenergie von Molekülen.
Wichtig wird das zum Beispiel in der Halbleiterphysik: Zinkoxid ist ein Halbleiter, der sich dadurch auszeichnet, dass er eine sehr große Energielücke zwischen den besetzten und den unbesetzten Zuständen der Elektronen hat. Er ist deshalb für sichtbares Licht durchsichtig und kann darum zum Beispiel verwendet werden, um Kontakte für Leuchtdioden oder Solarzellen herzustellen. Reines Zinkoxid ist ein sogenannter n-Halbleiter, also einer, bei denen Elektronen den Strom tragen (Bei p-Halbleitern sind es Fehlstellen, so genannte Löcher, die für die Leitung verantwortlich sind.) Warum Zinkoxid ein n-Halbleiter ist, ist allerdings nicht ganz klar. Eine Möglichkeit besteht darin, dass das Material bei der Herstellung Wasserstoff einlagert, der dann Elektronen abgeben kann. Um die Energien für die Einlagerung von Wasserstoff zu berechnen, muss man die Energie des Wasserstoffs im Material mit der von molekularem Wasserstoff vergleichen – und genau dabei kommt die Nullpunktsenergie ins Spiel. Nur wenn man die berücksichtigt, ergeben sich korrekte Werte für die Energien. Die Berechnungen zeigen, dass es tatsächlich plausibel ist, dass Wasserstoff für die Eigenschaften von Zinkoxid verantwortlich ist – allerdings ist das nicht eindeutig geklärt.
Die Nullpunktsenergie ist vor allem dann wichtig, wenn ihr zwei Zustände vergleicht, die sich in ihren Schwingungsmöglichkeiten unterscheiden. Ein Beispiel hierfür ist Wasser. Im (flüssigen) Wasser bilden sich ständig kleine Gruppen (“Cluster” genannt) von Molekülen, die eine Weile zusammenhalten und sich dann wieder lösen. (Weil diese Cluster eine Weile halten, hat Wasser tatsächlich ein “Gedächtnis” für seine Struktur – allerdings müsst ihr eure homöopathischen Mittelchen, die darauf beruhen, seeeehr schnell einnehmen, denn das Gedächtnis hält nur so etwa 0,0000000000001 Sekunde – vielleicht auch eine Null mehr oder weniger…)
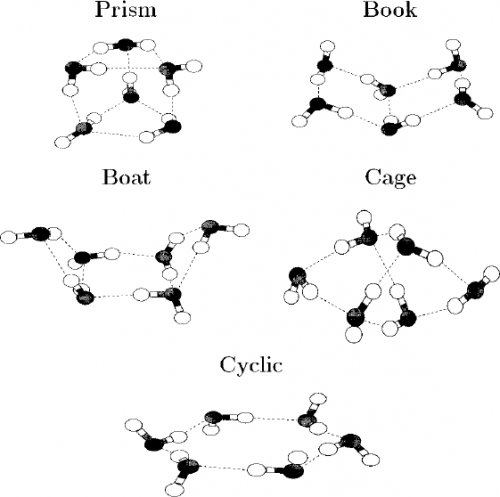
Cluster können unterschiedliche viele Wassermoleküle enthalten. Hier einmal ein paar mögliche Strukturen für Sechser-Cluster (aus dem paper von Gregory/Clary):
Die Cluster haben dabei hübsche Namen, die grob die Form wiedergeben sollen. Berechnet man die Energien der Strukturen, dann ist zunächst die “Prisma”-Struktur (prism) die mit der absolut kleinsten Energie, gefolgt von der “Käfig”-Struktur (cage). Das Ergebnis ändert sich allerdings, wenn man die Nullpunktsenergie berücksichtigt, dann wird tatsächlich die Käfig-Struktur geringfügig günstiger. Auch hier ist also die Nullpunktsenergie wichtig, um die Eigenschaften des Moleküls genau zu verstehen.
Die Nullpunktsenergie ist also nicht nur einfach ein “buchhalterisches” Problem, das sich durch die Wahl des Energie-Nullpunkts quasi von selbst erledigt, sondern sie hat – zumindest in der Quantenmechanik – klar messbare Auswirkungen.
In der Quantenfeldtheorie – also der Quantentheorie der Elementarteilchen – hat auch das Vakuum eine Nullpunktsenergie, weil man Teilchen im Vakuum als “Schwingungsanregungen” betrachten kann, ganz ähnlich (zumindest mathematisch) wie die Schwingungen unserer Moleküle. Die physikalische Bedeutung dieser Nullpunktsenergie ist allerdings deutlich unklarer – berechnet man, wie groß sie etwa sein sollte, kommen gigantische Werte heraus, die so hoch sind, dass das Universum eigentlich sofort aufgrund dieser Energie und der daraus resultierenden Schwerkraft kollabieren sollte. Da es das nicht tut, haben wir da wohl irgend etwas noch nicht verstanden. Die Beispiele aus der Quantenmechanik zeigen aber zumindest, warum man in der Physik die Nullpunktsenergie nicht einfach unter den Teppich kehren sollte – wenn sie dort relevant ist und messbare Konsequenzen hat, warum sollte das in der Quantenfeldtheorie anders sein?
Die Relevanz der Nullpunktsenergie für atomistische Berechnungen ist mir gerade in diesem Buch begegnet:
Sholl, David, and Janice A. Steckel. Density functional theory: a practical introduction. John Wiley & Sons, 2011.
Die Berechnungen zum Zinkoxid findet ihr in
Chris G. Van de Walle, Hydrogen as a Cause of Doping in Zinc Oxide, Phys Rev Lett, 85 (2000), 1012
Und die Cluster im Wasser stammen aus
Gregory&Clary, Structure of Water Clusters. The Contribution of Many-Body Forces, Monomer Relaxation, and Vibrational Zero-Point Energy, J. Phys. Chem. 1996, 100, 18014-18022







Kommentare (34)