Wenn versucht wird, die Raumkrümmung zu veranschaulichen, dann sieht man oft das Bild eines großen Gummituchs, das von kleinen Kugeln, die Sterne oder Planeten darstellen sollen, eingedellt wird. (Auch hier auf den Scienceblogs wurde das schon erklärt – Florian hat in seinem Artikel auch auf einige Grenzen hingewiesen.) Auch anderswo wird dieses Modell verwendet, auch dort mit dem Hinweis, dass das Gummituch die Krümmung des Raumes veranschaulichen soll. Leider ist das – wie so oft bei anschaulichen Modellen – ein wenig problematisch..
Hier ein Bild, wie man sich ein solches Gummituch-Modell vorstellen kann:

(Quelle: University of New Mexico)
In der üblichen Erklärung entspricht das Gummituch dem Raum und die Verzerrung des Tuchs soll die Verzerrung des Raums und damit die Raumkrümmung darstellen. Ein bisschen problematisch mag dabei erscheinen, dass wir dabei ja die Schwerkraft der Kugeln benutzen, um die Dellen zu erzeugen, und in gewisser Weise Schwerkraft mit Schwerkraft erklären:

Das ist aber nicht wirklich das Hauptproblem dieses Modells. Es ist nämlich in Wahrheit gar kein Modell der Allgemeinen Relativitätstheorie mit ihrer Raumkrümmung, sondern ein Modell der ganz gewöhnlichen Newtonschen Theorie der Schwerkraft. (Das erklärt übrigens auch sehr schön der englische Wikipedia-Artikel zum Thema “Gravity Well”, aus dem ich mich hier auch reichlich bediene…)
Fangen wir erst einmal bei der klassischen Schwerkraft an. Nach Newton ziehen sich massive Gegenstände mit einer Kraft an – beispielsweise die Erde und die Sonne, oder die Erde und ein Raumschiff. Das Raumschiff hat den Vorteil, dass es so viel leichter ist als die Erde, dass wir die Schwerkraft des Raumschiffs und deren Einfluss auf die Bewegung der Erde vernachlässigen können.
Nehmen wir an, unser Raumschiff steht auf der Erdoberfläche – wir hätten es aber gern (frei nach Loriot) in einer ruhigen, erdnahen Umlaufbahn. Dazu brauchen wir eine Kraft, mit der wir das Raumschiff anheben. Diese Kraft muss so groß sein wie die Schwerkraft (in Wahrheit eine Winzigkeit größer, damit sich das Raumschiff auch bewegt, aber diese Feinheit ignorieren wir einfach). Die Schwerebeschleunigung an der Erdoberfläche ist 9,81Meter pro Sekunde pro Sekunde (oft mit g abgekürzt), und gegen die müssen wir anarbeiten. Dank Herrn Newton wissen wir, dass Kraft gleich Masse mal Beschleunigung ist, die Kraft ist also die Masse unseres Raumschiffs mal g. Um das Raumschiff einen Meter anzuheben, muss diese Kraft über eine Strecke von einen Meter wirken. Die Energie, die wir dazu brauchen, ist gleich der Kraft mal dem Weg – insgesamt landen wir also für die Energie bei der Formel Energie = Masse mal Schwerebeschleunigung mal Weg, oder kurz E=m g h.
Wir können also die Energie unseres Raumschiffs als Funktion der Höhe aufschreiben, und dafür gilt zunächst einmal diese Formel. (Man darf dabei den Ort, bei dem die Energie gleich Null ist, frei wählen – warum das geht, diskutiere ich heute aber nicht, das habe ich vor langer Zeit schon gemacht.)
Wenn wir unser Raumschiff weiter anheben, dann gilt diese Formel allerdings irgendwann nicht mehr. Denn je weiter wir uns von der Erde entfernen, desto schwächer wird die Anziehungskraft (auch wenn sie in einer Umlaufbahn um die Erde nicht null ist). Die Schwerkraft nimmt ja – auch das hat Newton rausgeknobelt, der war schon ganz schön clever – mit dem Quadrat des Abstands ab – wenn wir unser Raumschiff doppelt so weit von der Erde entfernen, dann sinkt die Kraft auf ein Viertel. Achtung: Doppelt so weit heißt natürlich nicht, dass wir es zwei statt einen Meter anheben – die Entfernung ist immer die zum Erdmittelpunkt. Damit die Kraft auf ein Viertel sinkt, müssen wir unser Raumschiff also einen Erdradius (etwa 6371 Kilometer) anheben.
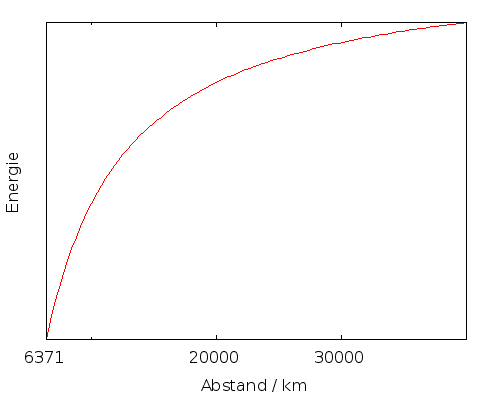
Berücksichtigt man das, wird die Formel für die Energie unseres Raumschiffs etwas komplizierter. Hier ist eine Kurve der Energie (ohne Einheiten für die Energie – der Wert der Energie hängt ja von der Masse unseres Raumschiffs ab) die zeigt, wie die Energie verläuft:
Auf der x-Achse ist dabei der Abstand vom Erdmittelpunkt aufgetragen, und die Kurve fängt bei einem Erdradius an.
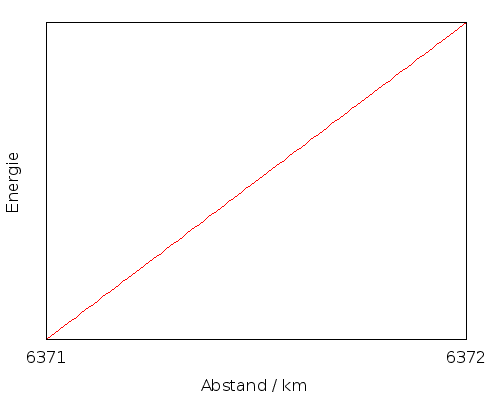
Zoomt man genau bei einem Erdradius in die Kurve hinein, sieht man, dass unsere einfache Formel, bei der die Energie einfach mit der Höhe zunimmt, für kleine Abstände von der Erdoberfläche gut passt – die Kurve ist nahezu perfekt eine Gerade:
Wir können jetzt also die Energie unseres Raumschiffes (zumindest prinzipiell) an Hand dieser Bildchen bestimmen, wenn wir seine Höhe kennen. Das Ganze vereinfacht sich noch etwas, wenn wir zwei Überlegungen anstellen:
1. Wenn wir die Masse des Raumschiffs ändern, dann ändert sich auch die Energie, und zwar genau proportional zur Masse. (Das steckt ja gerade in der Gleichung Kraft gleich Masse mal Beschleunigung: Doppelte Masse gibt doppelte Kraft und damit auch doppelte Energie.) Wir können also eigentlich die Masse des Raumschiffs herausdividieren – dann bekommen wir eine Größe, die das Schwerefeld der Erde selbst charakterisiert, das Potential. Multipliziert man das Potential mit der Masse eines Objekts, erhält man die Energie des Objekts am jeweiligen Ort.
2. Im Moment haben wir den Nullpunkt der Energie (oder des Potentials) genau bei Höhe Null gewählt. Das ist aber eine ziemlich willkürliche Wahl. Wenn wir uns fragen, wie sich die Energie eines Objekts ändert, wenn die Schwerkraft der Erde ins Spiel kommt, dann ist es am einfachsten, den Energienullpunkt so zu wählen, dass das Objekt eine Energie von Null hat, wenn es vom Schwerefeld der Erde nichts merkt. Und das ist dann der Fall, wenn es sehr sehr weit (mathematisch unendlich weit) von der Erde entfernt ist. Nähert sich das Objekt der Erde an, wird seine Energie dann immer kleiner, also negativ. Das klingt vielleicht erst mal seltsam, ist aber sehr praktisch: Nehmt an, ihr lasst das Objekt los und es fällt zur Erde. Dabei wird es natürlich – weil es auf die Erde zufällt – immer schneller und bekommt deshalb Bewegungsenergie. Diese Bewegungsenergie ist natürlich positiv, und sie ist genau gleich der negativen Energie im Schwerefeld, so dass die Summe immer noch Null ergibt.
Also: Wir haben jetzt ein Potential, das ein Maß für die Energie eines Objekts im Schwerefeld ist (wenn wir die Masse des Objekts ranmultiplizieren, bekommen wir die Energie). Das Potential ist gleich Null, wenn wir sehr weit von der Erde (oder was sonst gerade das Schwerefeld erzeugt) entfernt sind. Trägt man das Potential gegen den Abstand auf, dann bekommt man genau dieselbe Kurve wie oben für die Energie (nur jetzt mit anderen Einheiten, aber da ich die ja eh weggelassen hatte, macht das nichts).
Das Potential hängt dabei nur vom Abstand ab – es ist egal, ob ich über dem Nordpol, über Braunschweig oder über Kapstadt herumschwebe – wenn der Abstand von der Erdoberfläche derselbe ist, ist auch die Energie dieselbe. (Naja, nicht ganz, weil die Erde etwas ungleichmäßig geformt und inhomogen ist, aber das sind so Effekte, die ich als theoretischer Physiker locker unter den Teppich kehre.) Wir können also jedem Punkt im Raum einen Wert des Potentials zuordnen – aber das lässt sich schlecht grafisch darstellen. Deswegen lässt man meist eine Dimension beim Zeichnen weg und zeichnet einen zweidimensionalen Schnitt des Potentials. So sieht er aus (dabei ist angenommen, dass die Erde im inneren vollkommen homogen ist, aber das Potential im Erdinnern ist für uns erst mal egal):

(Bild von AllenMcC, Wikimedia, CC 3.0 License)
Im Englischen nennt man so etwas auch “gravity well” – im Deutschen spricht man manchmal vom “Potentialtopf”, auch wenn der hier nicht sehr topfförmig ist.
Wenn sich ein Objekt in einem solchen Potential bewegt, dann gewinnt es – wie ja eben schon erklärt – an kinetischer Energie, je tiefer es in den Topf hineinrutscht. Die Höhe des Objekts gibt direkt seine Energie an- je tiefer es ist, desto geringer ist seine Energie. (Bindungsenergien werden in der Physik generell negativ gerechnet, warum das sinnvoll ist, habe ich hier erklärt.)
Stellt euch vor, ihr würdet das Bild oben nehmen und diese Fläche in einem 3D-Drucker nachbauen und gerade hinstellen. Jetzt legt ihr ein kleines Objekt an den Rand des Trichters – es wird natürlich in den Trichter hineinrutschen, weil es ja von der Erde angezogen wird. Die Energie des Objekts ist jetzt um so kleiner, je tiefer es rutscht. Weil der Trichter auf der Erdoberfläche steht und nicht unglaublich riesig ist, ist die potentielle Energie, die unser Objekt im Schwerefeld der Erde hat, also genau proportional zur Höhe seines Ortes im Trichter.
Das klingt vielleicht etwas verwirrend, weil wir erst ein Trichtermodell der Schwerkraft bauen und dann die Schwerkraft nehmen, um die Energie unseres Objekts in diesem Modell darzustellen. (Das war ja genau das Problem des Comics oben.) Wenn euch das verwirrt, dann stellt euch stattdessen vor, ihr wärt mit dem Trichter irgendwo im Weltall, weit weg von jedem Schwerefeld. Dann ist die Energie des Objekts erst einmal völlig unabhängig davon, wo es im Trichter sitzt. Als nächstes schaltet ihr ein elektrisches Feld ein, das homogen ist und genau nach unten zeigt. Wenn euer Objekt eine elektrische Ladung trägt, dann wird es jetzt vom elektrischen Feld nach unten gezogen, und je tiefer es sitzt, desto kleiner ist seine Energie. Es ist nur wesentlich einfacher, das Ganze mit der Schwerkraft zu realisieren – jetzt ist es eben die Schwerkraft an der Erdoberfläche (wo die Energie in sehr guter Näherung genau proportional zur Höhe ist) mit der wird die Energie innerhalb des Trichters einstellen.
Die Energie unseres Objekts ist also proportional zu seiner Höhe im Trichter. Wenn wir es jetzt in den Trichter hineinrutschen lassen, dann gewinnt es natürlich an Geschwindigkeit. Das ist ganz analog zu dem, was wir uns oben im Schwerefeld überlegt hatten – lasse ich ein Teilchen los, dann nimmt die Bewegungsenergie in genau dem Maße zu, in dem die Energie im Schwerefeld abnimmt. Wenn wir ein Objekt in unserem Modelltrichter herumrutschen lassen, dann ändert sich seine kinetische und seine potentielle Energie also genau so, wie sie es auch bei einem echten Teilchen im Schwerefeld tun würden.
Allerdings stimmt das nur näherungsweise. In unserem Trichter saust das Teilchen ja nicht nur nach Innen, sondern auch nach unten. Ein Teil der kinetischen Energie gehört also zur Geschwindigkeit in der senkrechten Richtung. Diese Geschwindigkeit gibt es bei dem Teilchen, das sich im Schwerefeld bewegt, natürlich nicht. Wir betrachten ja nur einen zweidimensionalen Ausschnitt und die dritte Dimension in unserem Modell hat nichts mit der dritten Dimension im Raum zu tun, sie ist ja nur ein Maß für die Energie. Wenn wir die Bewegung unseres Teilchens angucken, dann interessiert uns nur die Geschwindigkeit innerhalb der Ebene (also die, die ihr seht, wenn ihr genau senkrecht von oben auf das Gummituch guckt.) Und da sind die Teilchen dann in diesem Modell ein bisschen langsamer als sie es sein sollten, weil ein Teil der Energie eben in die senkrechte Geschwindigkeitskomponente geht. Je flacher unser Potential ist, desto kleiner ist dieser Störeffekt, aber wir können ihn nie ganz loswerden.
Darüber hinaus nimmt man bei solchen Modellen meist Kugeln. Kugeln rollen, was praktisch ist, weil dann die Reibung klein ist (Reibung ist ein weiteres Problem mit diesem Modell.) Ein Teil der Energie, die eine Kugel gewinnt, wenn sie im Trichter nach unten rollt, wird aber in Rotationsenergie umgesetzt, weil die Kugel sich ja um ihre Achse dreht. Diese Rotationsenergie fehlt entsprechend bei der kinetischen Energie – die Kugel rollt also nicht ganz so schnell, wie sie eigentlich sollte. (Deswegen habe ich auch oben von einem “Objekt” gesprochen.)
Also: Wenn man ein Trichtermodell nimmt, dann kann man in einem solchen Modell Kugeln herumrollen lassen – die bewegen sich dann zumindest näherungsweise so, als würden sie sich in einem Schwerefeld bewegen. Da in der klassischen Physik die Gleichungen für die elektrische und die gravitative Anziehung zwischen zwei Körpern genau dieselbe Form haben, können wir unseren Trichter auch als Modell für die elektrische Anziehung zwischen zwei Körpern verwenden. Wir können auch die Abstoßung darstellen, dazu müssen wir den Trichter nur umdrehen.
Und wie kommt jetzt das Gummituch ins Spiel? Wenn man ein Gummituch elastisch dehnt, dann braucht man dafür Energie (das kommt nicht daher, dass man da Bindungen im Gummi dehnt, gegen deren Kraft man anarbeiten muss, sondern ist ein trickreicher Effekt der Entropie). Stellt euch also vor, ihr spannt ein Gummituch an den Rändern ein (so wie in dem verlinkten Bild oben) und drückt es jetzt (erst mal mit dem Finger) nach unten (oder ihr zieht es nach oben, das ist im Moment egal). Je weiter ihr es zieht, um so mehr Energie braucht ihr dafür. Die Energie hängt also davon ab, wie stark das Gummituch nach oben oder unten gedehnt wird.
Statt am Gummituch zu ziehen, könnt ihr auch kleine schwere Kugeln drauflegen – auch die üben (dank der Schwerkraft) eine Kraft nach unten aus. Diese verformen das Gummi. Um die Kugeln herum wird das Gummi natürlich auch nach unten gezogen – die Kugeln erzeugen eine schöne große Delle, wie man das ja auch im Bild oben sieht. Und jetzt kommt der Trick des Ganzen: Die Gleichung, die angibt, wie weit das Gummituch nach unten ausgelenkt wird, sieht genau so aus wie die Gleichung für das Gravitationspotential (allerdings natürlich in zwei Dimensionen). Wenn wir also Massen in einem Gummituch platzieren, dann verzerren diese das Gummituch genau entsprechend dem Bild unseres Trichters oben. Und wenn ihr zwei oder drei Massen platziert, dann klappt das immer noch – ihr könnt also auch kompliziertere Anordnungen von Massen und deren Schwerefeld simulieren.
Hier nochmal die Gedankenkette, die zum Gummituchmodell führt, in Kurzform:
1. Die Energie eines Teilchens in einem Schwerefeld wird durch das Potential gegeben.
2. Weil die Energie im Schwerefeld direkt auf der Erdoberfläche proportional zur Höhe ist, kann ich ein zweidimensionales Modell eines Potentials verwenden, so dass ein Teilchen gerade die Energie hat, die seiner Höhe in diesem Potential entspricht.
3. Ein Teilchen, das durch ein solches Trichtermodell rollt, verhält sich deshalb näherungsweise (bis auf Probleme mit Reibung, der Geschwindigkeit in der dritten Dimension und der Rotationsenergie) wie ein Teilchen in einem solchen Schwerefeldpotential es tun würde.
4. Statt mühsam ein Potentialmodell zu berechnen und dann im 3D-Drucker herzustellen, kann ich auch einfach ein Gummituch nehmen – dieses wird durch hineingelegte Massen genau so verzerrt, dass die Höhe des Gummituchs so aussieht wie der Potentialtrichter im Schwerefeld.
Das Gummituchmodell ist also ein sehr praktisches Modell, um die Bewegung von Teilchen im Schwerefeld zu simulieren. Allerdings haben wir uns hier die ganze Zeit innerhalb der klassischen Physik bewegt. Was hat denn nun das Modell mit der Raumkrümmung zu tun?
Die ebenso einfache wie traurige Antwort lautet: Nichts. Absolut überhaupt gar nichts. Obwohl dieses Modell ständig gezeigt und verwendet wird, um die Raumkrümmung zu erläutern, hat es mit der Raumkrümmung wirklich nichts zu tun. Weder ist der Raum in einem Schwerefeld so gekrümmt wie das Gummituch, noch bewegen sich Teilchen auf Grund der Raumkrümmung so, wie sie es im Gummituchmodell tun.
Warum das Modell dann trotzdem ständig verwendet wird? Weil das verzerrte Gummituch auf den ersten Blick so aussieht wie eine Darstellung des gekrümmten Raumes. Aber das näher zu erläutern, braucht wohl einen zweiten Teil – mehrteilige Posts hatte ich ja schon eine Weile nicht…






Kommentare (84)