Das Modell des Gummituchs, das sich durchbiegt, wenn man Massen drauflegt, ist ein brauchbares Modell für das Potential des Schwerefelds – allerdings in der klassischen Physik nach Newton. Das habe ich im ersten Teil dieses Textes erklärt. Wie kommt es aber, dass man das Modell so oft im Zusammenhang mit der Allgemeinen Relativitätstheorie (kurz ART) sieht? Passt es da vielleicht auch hin und veranschaulicht die Krümmung des Raumes?
Die Raumkrümmung (eigentlich ist es eine Raum-Zeit-Krümmung, aber erst einmal konzentrieren wir uns auf den Raum) habe ich ja neulich schon etwas ausführlicher erklärt. Kurz gesagt sorgt sie dafür, dass sich Abstände (zum Beispiel die Länge von Maßstäben) von Ort zu Ort ändern können. Mein Lieblingsbeispiel ist die Raumkrümmung um eine massive Kugel herum: Wenn ihr einen Kreis um die Kugel malt und dessen Umfang messt, dann sollte der ach der Gleichung U=2πr mit dem Radius zusammenhängen. Wenn ihr aber tatsächlich ins Innere der Kugel eindringt und den Weg messt, dann stellt ihr fest, dass dieser Weg länger ist, als ihr nach dieser Formel erwarten würdet. Es ist sozusagen nach Innen hin “mehr Raum” da, als man eigentlich erwarten würde (das ist eine etwas ungenaue Beschreibung, aber als Veranschaulichung finde ich sie ganz gut). Andersherum kann man auch sagen: Für eine bestimmte Entfernung in Richtung auf den Mittelpunkt zu ist nicht genug Umfang vorhanden.
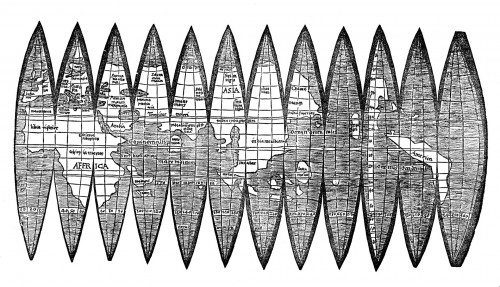
Man kann sich das ganz gut mit einer zweidimensionalen gekrümmten Fläche vorstellen. Wen ihr zum Beispiel eine Mandarine oder Orange schält, und zwar so, dass ihr die Schale möglichst in einem Stück abbekommt, dann könnt ihr die Schale nicht flach auf einem Tisch ausbreiten – wenn ihr das tut, reißt sie ein. Man sieht das auch sehr schön an dieser (sehr alten) Karte, die zur Herstellung von Globen (Globussen, Globunten, Globuli – ach ne, das ist was anderes…) diente:
(Bild von Wikimedia, Public domain)
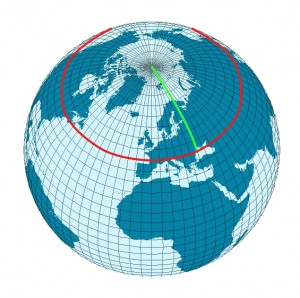
Ihr könnt euch das direkt mit Hilfe von Längen- und Breitengraden veranschaulichen: Je weiter ihr nach Norden geht, um so kürzer wird der Abstand zwischen zwei Längengraden, bis sie dann schließlich am Nordpol alle zusammenlaufen. Das entsprechende Bild von Kreisumfang und -radius habe ich ja schon des öfteren gezeigt:
(Achtung: Bei solchen Analogien läuft man immer Gefahr, durcheinanderzukommen: Es ist die Oberfläche der Erde, um die es jetzt geht, nicht die Erde als Ganzes. Das Innere der Erde ist für die Krümmung irrelevant, und der Mittelpunkt der Erde hier hat nichts mit dem Mittelpunkt zu tun, um den es im vorigen Absatz ging und von dem aus wir den Radius gemessen haben.)
Wen ihr also die Krümmung einer zweidimensionalen Fläche veranschaulichen wollt, dann könnt ihr sie dazu in drei Dimensionen zeichnen, so wie den Globus. (Na klar, der Globus ist tatsächlich ein Objekt in drei Dimensionen – aber das muss für eine gekrümmte Fläche nicht unbedingt gelten; ihr könnt sie auch komplett mit Hilfe von flachen Landkarten beschreiben.) Eine solche Darstellung nennt man auch eine “Einbettung” – die gekrümmte Fläche wird in eine höhere Dimension gepackt oder eben eingebettet.
Um den gekrümmten dreidimensionalen Raum in der ART darzustellen, könnten wir jetzt genauso versuchen, ihn in einem höherdimensionalen Raum darzustellen. (Für den allgemeinen Fall braucht man dazu in der ART aber nicht nur vier, sondern sogar fünf Dimensionen, plus eine Zeitdimension.) Ein Objekt in 4 oder mehr Dimensionen können wir uns aber nicht so leicht vorstellen. Entsprechend begnügt man sich damit, nur einen zweidimensionalen Ausschnitt einzubetten. Damit es nicht zu übermäßiger Verwirrung mit den Globus-Bildern oben kommt, nehme ich jetzt als massives Objekt nicht die Erde, sondern die Sonne:
(Bild mit gimp erzeugt, die Oberfläche der Sonne von Wikimedia, Public domain)
Wir betrachten jetzt eine Schnittebene durch die Sonne (genau durch ihren Mittelpunkt, naja, hab ich nicht ganz perfekt gezeichnet), etwa so:
Jetzt haben wir eine zweidimensionale Ebene im Raum. Diese Ebene ist aber – wegen der Raumkrümmung – eben gekrümmt. Wenn wir also den Umfang des roten Kreises messen und daraus den Sonnenradius berechnen, kommen wir auf einen anderen Wert, als wenn wir tatsächlich die Strecke bis zur Mitte der Sonne ausmessen (der Unterschied beträgt etwa 500 Meter, das ist bei einem Sonnenradius von etwa 700000 Kilometern nicht schrecklich viel, aber immerhin).
Genau wie bei der Orange von vorhin oder bei dem Schnittmuster für den Globus “fehlt” uns also etwas Raum, wenn wir versuchen würden, den Raum tatsächlich “flach” zu drücken. Wir können, um das zu veranschaulichen, den Raum um die Sonne herum (aber nur unseren Schnitt entlang der Ebene) in den dreidimensionalen Raum einbetten und sehen, was passiert. Das Ergebnis sieht so aus:
In der Mitte sitzt hier die Sonne (da wo die Fläche eher wie eine Kugel gekrümmt ist). Ihr seht auch in diesem Diagramm, dass ihr eine größere Strecke bis zum Mittelpunkt der Sonne zurücklegen müsst, als ihr eigentlich erwarten würdet, wenn ihr nur den Umfang eines Kreises betrachtet:
Ein solches Bild bezeichnet man auch als Einbettungsdiagramm. Man kann es auch direkt in ein dreidimensionales Bild hineinzeichnen, obwohl das ein bisschen verwirrend ist – zur Veranschulichung wird das aber gern gemacht, etwa so:
(Bild von Wikimedia, Public domain)
Ein solches Bild ist ein bisschen irreführend, weil die dritte Dimension hier gleich eine Doppelrolle spielt – zum einen wird sie verwendet, um zu zeigen, wie sich Strecken ändern, wenn man dichter an die Sonne herangeht, zum anderen braucht man sie aber auch für die 3D-Darstellung der Sonne und des ganzen anderen Krams im Bild. (Die dargestellte Raumkrümmung entspricht auch eher der Form eines Newton-Gravitationspotentials, aber das ist bei solchen Darstellungen auch oft so – auch bei dem Bild, das ich gleich zeige.)
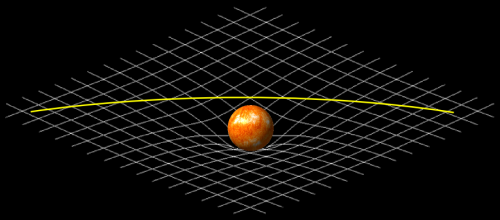
Wichtig an den Einbettungsdiagrammen ist, dass man sie – wie wir eben am Bild mit dem Kreis gesehen haben – verwenden kann, um zu sehen, wie sich Strecken ändern, wenn man einen gekrümmten Raum durchquert. Die Diagramme werden aber auch gern verwendet, um zu zeigen, wie sich Objekte in der Raumzeit bewegen. Beispielsweise wird die Lichtablenkung gern mit solchen Bildern dargestellt (siehe auch das Bild eben, wo ja auch ein Signal abgelenkt wird)):
(Bild der Raumkrümmung von Wikimedia, CC License 3.0; mit Inkscape und gimp modifiziert. Auch hier ist die Raumkrümmung quantitativ falsch.)
Solche Bilder sind allerdings problematisch. Die Bewegung von Licht oder von Teilchen wird nämlich nicht nur durch den gekrümmten Raum beeinflusst, sondern durch die Krümmung der Raumzeit – dass die Zeit in der Nähe eines Schwerefelds anders verläuft, spielt eine wichtige Rolle, wie ich neulich ja schon erklärt habe.
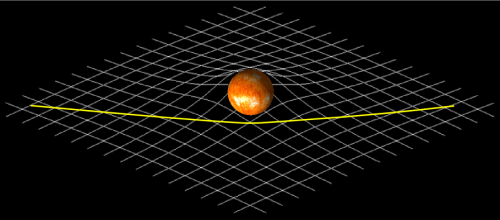
Wenn wir aber einmal den Aspekt der veränderten Zeit ignorieren, dann sehen wir bei Bildern dieser Art immer noch folgendes: Der Lichtstrahl nimmt hier den kürzesten Weg (wie gesagt, das stimmt nicht ganz wegen der Zeitkomponente) – die Raumkrümmung wirkt eben dadurch, dass in der Nähe der Masse Strecken verändert sind. Es spielt deshalb überhaupt keine Rolle, wie wir unser Bild zeichnen. Wir könnten es beispielsweise genausogut herumdrehen (ich hätte eigentlich die Sonne jetzt unter die gekrümmte Fläche malen sollen, aber das war mir zu viel Arbeit…):
Entscheidend ist einzig und allein, dass sich Längen verändern – ob die Krümmung nach oben oder unten läuft, spielt überhaupt keine Rolle.
So, und jetzt kommen wir zurück zum Gummituch. Hier noch einmal das Bild des Gravitationspotentials vom letzten Mal

(Bild von AllenMcC, Wikimedia, CC 3.0 License)
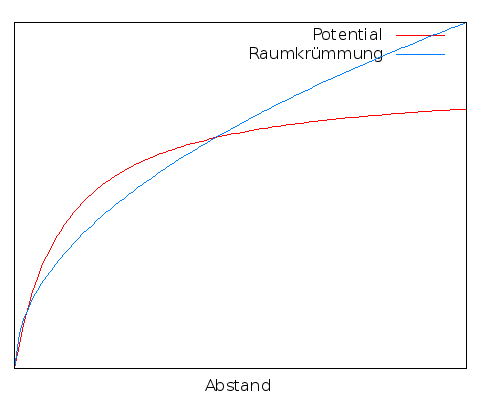
Dieses Bild zeigte die Energie (oder das Potential) eines Teilchens im Schwerefeld an. Zunächst einmal sieht man, wenn man es mit dem Bild des gekrümmten Raums oben vergleicht, dass die Form eine andere ist – auch mathematisch passen die beiden Bilder nicht zusammen.Hier ein direkter Vergleich der Form als Funktion des Abstands – einmal für das Potential (oder eben die Form des Gummituchs, in rot), einmal für die Form des Modells des gekrümmten Raums (blau):
Das allein ist schon ein gutes Argument dafür, dass das Bild des Gummituchs (das ja auf diesem Potential beruhte) nicht viel mit der Raumkrümmung zu tun hat.
Aber gut – auch wen es mathematisch nicht so gut passt, ist es vielleicht doch eine gute Veranschaulichung, oder? Nein, leider nicht. Dazu muss man sich nur überlegen, was passiert, wenn man das Gummituch beispielsweise einfrieren und dann umdrehen würde. Im Bild des gekrümmten Raumes ist das vollkommen egal, wie wir gerade gesehen haben. Eine Kugel, die über unser umgedrehtes Gummituch rollt, benimmt sich aber ganz anders als eine, die auf dem normalen Gummituch herumkullert – auf dem umgedrehten Tuch wird die Kugel ja von den Beulen im Tuch abgestoßen und nicht angezogen. Die Bewegung der Kugeln auf dem Gummituch wurde ja durch die Schwerkraft (die hier konstant war und dafür sorgte, dass sich die Energie der Kugel proportional zur Höhe des Tuchs ändert) bestimmt – im Bild der Raumkrümmung aber spielt das gar keine Rolle, denn da geht es nur darum, welche Wege die kürzesten sind. (Das passt auch zu der Aussage, dass es in der ART gar keine Schwerkraft gibt – entsprechend ergibt es auch wenig Sinn, von potentieller Energie zu reden.)
Hmm – aber wie funktioniert eigentlich die Anziehung in unserem Raumkrümmungsmodell?
Erst einmal gar nicht. Wenn ihr eine Kugel irgendwo platziert, ohne dass sie sich bewegt, und es keine Anziehung oder so etwas gibt, dann würde die Kugel einfach am Ort verharren. Dass reale Kugeln sich bewegen, liegt an der Krümmung der Raumzeit. Die sorgt dafür, dass eine ruhende Kugel, die sich in der Nähe einer Masse befindet und bei der deshalb die Raumzeit gekrümmt ist, bewegt. Wie das? Ausführlich habe ich das auch hier erklärt – kurz gesagt liegt es daran, dass eine Bewegung im freien Fall in der gekrümmten Raumzeit dem entspricht, was eine Bewegung mit konstanter Geschwindigkeit in einer ungekrümmten Raumzeit ist. Ein Objekt im freien Fall folgt sozusagen der natürlichen Bahn in der Raumzeit (so wie in der klassischen Physik nach Newton ein kräftefreies Objekt mit konstanter Geschwindigkeit weiterfliegt, das ist das berühmte erste Newtonsche Axiom).
Das ist übrigens noch ein weiteres Argument gegen das Gummituchmodell: Die Krümmung des Raums allein reicht nicht aus, um die Bewegung von Teilchen zu erklären – und tatsächlich wird sich kein Teilchen (und auch kein Lichtstrahl) auf der Bahn bewegen, die im gekrümmten Raum der kürzesten Strecke entspricht, weil die Zeitkomponente der Raumzeit dies verhindert. (Das habe ich ja neulich ganz ausführlich auseinandergedröselt.) Sonst wäre es auch nicht zu erklären, dass die ART und das Newtonsche Modell in den meisten Fällen sehr ähnliche Vorhersagen machen – die Bahnen der Planeten werden ja, abgesehen von dem sehr winzigen Effekt der Periheldrehung, von beiden Theorien gleich gut vorhergesagt.
Das Gummituch-Modell illustriert eigentlich nur eins: Dass Massen den Raum irgendwie krümmen.Die Krümmung im Gummituch-Modell sorgt aber nicht dafür, dass Kugeln in diesem Modell auf kürzesten Verbindungen zwischen zwei Raumzeitpunkten laufen (so wie sie es in der ART tun), sondern dafür, dass sich die Energie von Ort zu Ort so ändert, wie sie es in der klassischen Physik tut. Die Bewegung von Teilchen in diesem Modell stimmt zwar mit der Bewegung von Teilchen in der ART näherungsweise überein, aber eben nicht, weil das Modell ein gutes Modell der Raumkrümmung ist, sondern weil die Energielandschaft der klassischen Physik für nahezu die selben Bewegungen sorgt wie die gekrümmte Raumzeit der ART.
Als echtes Modell der Raumkrümmung versagt das Modell also gleich in mehrfacher Hinsicht: Zum einen stimmt die Form schlicht und einfach nicht – die Verzerrung des Gummituchs ist zwar eine gute Näherung an ein Gravitationspotential, aber nicht an die gekrümmte Raumzeit. Zum anderen bewegen sich Teilchen im Gummituchmodell, weil sich ihre potentielle Energie von einem Ort zum anderen ändert – ein umgedrehtes Gummituch würde für eine Gravitationsabstoßung sorgen. Im Gegensatz dazu bewegen sich Teilchen im gekrümmten Raum (oder viel mehr der Raumzeit), weil sich Streckenlängen (und Zeitabläufe) ändern, nicht weil ihre Energie von Ort zu Ort eine andere ist. (Man kann aber die Newtonsche Theorie inklusive Energien aus der ART ableiten.) Und schließlich ignoriert das Bild völlig den Aspekt des veränderten Zeitablaufs, ohne den man die Bewegung eines Teilchens gar nicht verstehen kann – kein Teilchen bewegt sich auf den Bahnen, die im Modell des gekrümmten Raums die kürzesten sind.
Eigentlich ist es also höchste Zeit, sich vom Gummituchmodell zu verabschieden.











Kommentare (67)