Heute geht es mal wieder um Dino-Spuren – die waren hier ja schon öfters Thema. Heute aber geht es mal nicht um ein paper, das ich irgendwo gelesen habe, sondern um meine eigene Arbeit – ja ich habe mal wieder an Dinos geforscht.
Die Arbeit ist das Ergebnis eine Zusammenarbeit mit Peter Falkingham (einer unserer Studis an der TU Braunschweig hat auch noch mitgemischt) und basiert auf einer Veröffentlichung von ihm, die er vor ein paar Jahren geschrieben hat. Die Grundidee ist zunächst einmal sehr simpel: Stellt euch zwei Dinos (oder, wen ihr unbedingt wollt, andere Tiere) vor, die genau gleich aussehen, von denen der eine doppelt so lang ist wie der andere. Der Längere Dino ist dann acht mal so schwer wie der kleine (doppelt so lang, doppelt so breit und doppelt so hoch). Seine Füße aber haben nur die vierfache Fläche (sie sind doppelt so lang und doppelt so breit). Der Druck unter den Füßen des großen Dinos ist also 8/4=2 mal so groß wie der unter den kleinen Dinofüßen (denn Druck ist Kraft pro Fläche, und die Kraft ist die Gewichtskraft, also proportional zur Masse). Ein Boden, der weich genug ist, damit ein kleiner Dino (mit dem geringen Druck unter den Füßen) Spuren machen kann, ist dann möglicherweise für den großen Dino zu weich, und er würde dort tief einsinken und sich vielleicht nicht auf diesen Boden trauen.
Die Ausgangsfrage, die sich Peter stellte, war genau diese: Wie muss das Verhältnis von Bodeneigenschaften und Druckkraft sein, um Spuren hinterlassen zu können, die nicht zu tief sind (sonst würde das Tier sich auf diesen Boden ja vermutlich nicht drauf trauen) und auch nicht zu flach (sonst kann man von ihnen nicht mehr viel sehen). Man hätte das natürlich experimentell untersuchen können, aber solche Experimente sind vergleichsweise zeitaufwändig. Peter beschloss also, als Hilfsmittel den Computer zu nehmen, und die Entstehung von Fußabdrücken zu simulieren.
Seine Finite-Element-Modell (Finite Elemente (kurz FE) sind die Standard-Methode, um das Verhalten von Werkstoffen bei Belastung zu berechnen und mein tägliches Brot) war recht einfach, fast schon zu einfach. Er nahm an, dass der Fuß perfekt flach ist und dass er direkt auf dem Boden aufliegt und berechnete dann die Kraft, die zum Eindrücken in den Boden notwendig war. Effekte wie Reibung oder das Aufstauen von Material an den Seiten des Fußes (weil ja Boden unter dem Fuß weggedrückt werden muss) wurden in dieser Simulation vernachlässigt. Zudem wurde angenommen, dass der Boden ideal-plastisch ist – sobald eine bestimmte Spannung im Boden überschritten ist, verformt sich der Boden plastisch (wie Knetgummi) – größere Spannungen kann er nicht aufnehmen. (ExpertInnenhinweis: Das bezieht sich hier auf die von-Mises-Spannung, wie bei einfachen Plastizitätsmodellen üblich.)
Unter diesen einfachen Annahmen bekam er heraus, dass es nur einen sehr schmalen Druckbereich gibt, bei dem ein bestimmter Boden Spuren aufnehmen kann – ist der Druck geringfügig zu hoch, sinkt der Spurenmacher tief ein, ist er geringfügig zu niedrig, dann entstehen nur winzige Eindrücke. Natürlich war peter sich darüber im Klaren, dass das Modell eine Vereinfachung war – trotzdem fand er den Effekt interessant genug, dass er ihm einen Namen gab – Goldilocks-Effekt (Nach Goldlöckchen und den drei Bären, ihr wisst schon, da wo der Brei mal zu warm und mal zu kalt ist und nur einer genau richtig. Das Wort haben ja auch schon die AstronomInnen verwendet.) So etwa sah die Grafik aus, die Peter in seiner Arbeit verwendet hat (leicht modifiziert und farbig, weil ich sie für unser Poster adaptiert habe – auf dem Poster hatte ich noch ein paar Tyrannosaurier-Füße, die unterschiedlich tiefe Abdrücke hinterlassen, aber da ich den Fuß bei Jurassic Park geklaut habe, stelle ich den nicht ins Netz):
Horizontal ist hier die Festigkeit des Bodens aufgetragen, auf der senkrechten Achse der Druck. Nur bei genau passenden Werten landet man in der goldenen Goldilocks-Zone, sonst ist der Boden entweder zu weich oder zu hart.
Als ich das paper – mehr oder weniger per Zufall – las, dachte ich “Kann nicht sein.” Zum einen, weil ich aus der Alltagserfahrung wusste, dass z.B. an einem Strand sowohl ich als auch ein Kind gleichzeitig sichtbare Spuren hinterlassen können. Zum anderen, weil es in der Materialwissenschaft ein Standardverfahren ist, Eindrücke in Werkstoffe zu machen, um deren Festigkeit zu testen, und dort muss man nicht den Druck, mit dem man arbeitet, ganz genau einstellen, damit der Indenter nicht metertiefe Krater macht. Ich war also skeptisch.
Mehr oder weniger durch einen weiteren Zufall (über einen gemeinsamen Bekannten) bekam ich dann Kontakt zu Peter und wir trafen uns in Obernkirchen bei der großartigen Dino-Fußspur-Konferenz. Peter machte mir erst einmal klar, dass meine Vorstellung von Fußabdrücken eventuell etwas zu simpel ist – beim Menschen ist es wegen der gewölbten Fußfläche so, dass bei tieferen Eindrücken immer mehr Fußfläche mit dem Boden in Berührung kommt. Bei unseren Eindrücken zur Materialprüfung ist das ganz ähnlich – dort verwenden wir Kugeln oder diamantförmige Indenter – je größer die Kraft wird, desto größer ist die Fläche, die in Berührung kommt, so dass sich die Kraft auch weiter verteilt. Die meisten Vögel (und vermutlich auch Dinos) hatten aber eher flache Füße, so dass der Effekt dort kleiner sein sollte. Trotzdem war ich nicht überzeugt – bei einer genaueren Simulation, bei der Material verdrängt werden und sich aufstauen kann würde der Effekt größtenteils verschwinden, so meine Annahme.
Und wenn man sich in der Wissenschaft uneinig ist, so wie wir hier, dann ist der beste Weg, einfach zusammenzuarbeiten und zu sehen, was man herausbekommt. Und das taten wir dann auch. Ich bastelte also ein Fußspurenmodell, bei dem der Fuß auch tatsächlich tiefer in das Substrat eindringen kann und bei dem die Verdrängung von Material und die Reibung zwischen Fuß und Boden korrekt berücksichtigt werden sollten. Das erwies sich als etwas trickreicher als ursprünglich angenommen, aber schließlich klappte es.
(Wenn ihr es genau wissen wollt: Das Problem sind die sehr großen Deformationen im Boden, die durch die Verdrängung entstehen. Die führen zu einer starken Verzerrung des ursprünglichen Rechengitters, weil man bei der FE-Methode das Gitter an das Material anheftet. Zum Glück erlaubte die damals neuste Version meines FE-Programms schließlich, ein Gitter zu verwenden, das im Raum feststeht und durch das das Material durchfließt – damit ging es dann. Allerdings war ein bisschen Trickserei nötig, bis alles vernünftig herauskam – zum Glück fand ich einen Studi, der sich für’s Thema begeistern konnte, denn das Simulieren von Fußspuren ist ja nicht meine Hauptaufgabe…)
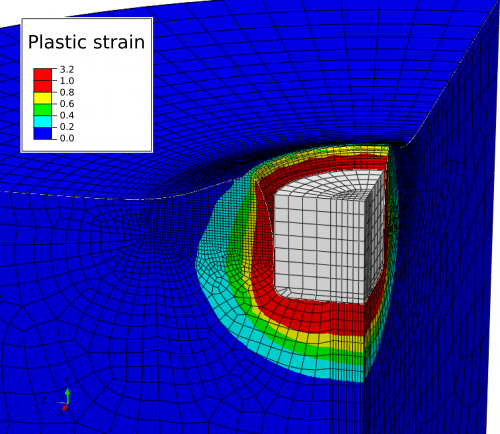
Da ich ja theoretischer Physiker bin, habe ich es mir dabei mit dem Fuß recht einfach gemacht und angenommen, dass der Fuß ein Zylinder (mit leicht abgerundeten Kanten) ist – das ist als sehr grobe Näherung an einen Sauropodenfuß vielleicht gar nicht so schlecht, und es ging ja auch und vor allem ums Prinzip. Wegen der Symmetrie habe ich nur ein viertel des Zylinders modelliert und den dann (wie gesagt, mit fleißiger Unterstützung eines Studis) in den Boden eindringen lassen, was etwa so aussah (die Farbe kennzeichnet, wie stark der Boden verformt wurde):
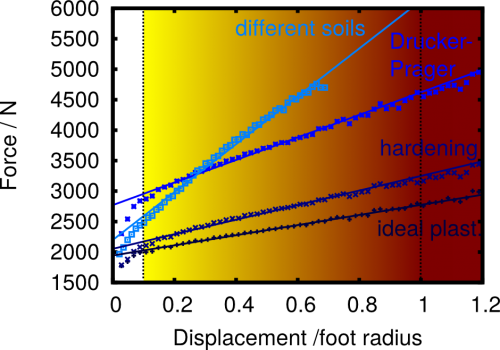
Und dann haben wir – für verschieden komplexe Bodenmodelle, auf die Details gehe ich aber nicht ein, wer die wissen will, kann ja ins paper schauen – die Kraft als Funktion der Eindringtiefe berechnet. So sah das Ergebnis aus:
Ihr seht, dass mit zunehmender Eindringtiefe (auf der horizontalen Achse) die Kraft ungefähr linear zunimmt. Es gibt also einen ganzen Bereich von Kräften, mit denen man Fußspuren erzeugen kann. Wir haben angenommen, dass der flachste Abdruck, den man noch erkennen kann, ein Zehntel des Fußradius groß ist, der tiefste Abdruck gleich dem Fußradius (noch tiefer einzusinken ist sicher unangenehm). Abhängig von den Annahmen, die man über den Boden macht, ergibt sich dabei ein mehr oder weniger großer Bereich von Kräften, mit denen man hier Abdrücke erzeugen kann. Der Goldilocks-Effekt ist also nicht so stark, wie ursprünglich angenommen, insbesondere dann nicht, wenn man komplexere Bodenmodelle annimmt, bei denen der Boden unter dem anliegenden Druck verfestigt oder bei dem unterschiedlich feste Bodenschichten übereinander liegen (“different soils” im Bild).
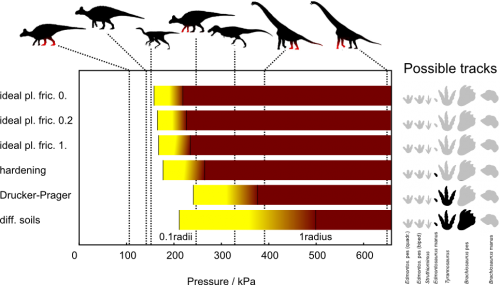
Aber ganz verschwunden ist der Effekt auch nicht. Peter hatte bereits für sein erstes paper den Druck berechnet, der bei diversen Dinos unter dem Fuß entsteht. Wenn man die Kraftkurven von oben verwendet und auf Drücke umrechnet, dann kann man sehen, welche Dinos auf welchen Böden Fußabdrücke hinterlassen können. Das hier kommt dabei heraus:
Hier seht ihr oben im Bild verschiedene Dinos – einen Edmontosaurus, einen Struthiomimus, einen T. rex und einen Brachiosaurus. Der Edmontosaurus taucht gleich drei mal auf – wenn er auf vier Beinen geht, ist der Druck unter den Hinterbeinen klein, der unter den Vorderbeinen deutlich größer; wenn er auf zwei Beinen geht, liegt er zwischen diesen beiden Extremen. Beim Brachiosaurus gibt es entsprechend einen Druckwert für die Hinter- und einen für die Vorderbeine.
Rechts im Bild seht ihr, welche Dinos jeweils auf einem Boden Spuren hinterlassen können und welche nicht (dass das grafisch einigermaßen schick ist liegt daran, dass ich das Bild für unser Poster aufgehübscht habe). Und links in der Hauptgrafik seht ihr die einzelnen Druckbereiche. (Die genauen Zahlenwerte der Böden sind dabei nur grob geschätzt – na klar findet man auch weichere oder festere Böden, es ging hier nurdarum zu sehen, wie groß der Bereich für eine bestimmte Bodensorte ist.)
Man sieht, dass die Wahrheit hier tatsächlich einmal in der Mitte liegt – der Goldilocks-Effekt ist nicht so stark, wie Peter in ursprünglich angenommen hatte, aber deutlich stärker, als ich vermutet hatte. Ja, auf ein und demselben Boden können unterschiedliche Dinos Spuren hinterlassen – aber nicht beliebig unterschiedliche. Man darf also zum Beispiel stark zweifeln, ob man an Hand von Fußspuren sagen kann, ob Dinos sich um ihre Jungen gekümmert haben – wenn man in den Spuren einer Herde nur große Fußabdrücke findet, kann das eben auch einfach daran liegen, dass die Mini-Dinos keine deutlichen Spuren mehr hinterlassen haben.
Natürlich ist damit das letzte Wort nicht gesprochen – unser Modell ist imer noch ziemlich vereinfacht. Die Fußgeometrie ist etwas simpel und wir haben nicht berücksichtigt, dass ein realer Fuß außen weiches Gewebe hat und innen harte Knochen, der Fuß bewegt sich genau senkrecht nach unten, die Bodenmodelle sind immer noch recht einfach und auch nicht mit experimentellen Daten unterfüttert. Es gibt also noch viel zu tun.
Aber ich habe immerhin meine zweite Veröffentlichung (sogar mit Open Access – wenn ihr wollt, könnt ihr also direkt reinschauen) im Bereich der Paläontologie – etwas, das ich mir nie hätte träumen lassen, als ich seinerzeit anfing, Physik zu studieren.
Peters Original-paper: Falkingham, P. L., et al. “The ‘Goldilocks’ effect: preservation bias in vertebrate track assemblages.” Journal of the Royal Society Interface 8.61 (2011): 1142-1154.
Falkingham, Peter L., Julian Hage, and Martin Bäker. “Mitigating the Goldilocks effect: the effects of different substrate models on track formation potential.” Royal Society Open Science 1.3 (2014): 140225.







Kommentare (28)