Welt ohne Spin

Der berühmte Spin von Elementarteilchen ist eine Eigenschaft, die wir uns nur schwer vorstellen können, weil es in der klassischen Physik so etwas nicht gibt. Gerade weil er so unanschaulich ist, ist es aber interessant, einmal zu sehen, welche Auswirkungen er eigentlich in unserer Welt hat. Wie würde eine Welt ohne Spin aussehen. Darüber mache ich mir heute mal ein paar Gedanken.

Wie so oft fange ich erst mal mit einer Warnung an: Ich habe diesen Artikel in ziemlich kurzer Zeit mehr oder weniger am Stück runtergeschrieben und die Ideen so aufgeschrieben, wie sie mir gerade einfielen. Es ist nicht unwahrscheinlich, dass ich dabei irgendwo etwas übersehen habe ohne einen wichtigen Aspekt ignoriere oder vielleicht auch irgendwo eine Folgerung falsch gezogen habe. Beschwert euch gern in den Kommentaren – ansonsten seid ihr natürlich eingeladen, selbst fleißig mitzuspekulieren.

Spin und Pauli-Prinzip

Wie gesagt- den Spin wirklich gut zu erklären, ist ziemlich schwierig. Ich habe es mal in diesem Artikel versucht (auch wenn der mitten in einer langen Serie steckt, könnt ihr ihn unabhängig vom Rest der Serie lesen). Kurz gesagt verhalten sich Teilchen wie Elektronen ein wenig so, als würden sie sich wie kleine Kreisel um ihre Achse drehen – oder physikalisch vornehm ausgedrückt, sie tragen einen inneren Drehimpuls. Man kann Elektronen aber nicht beim Drehen beschleunigen oder abbremsen – der Drehimpuls hat immer dieselbe Größe. Der Spin des Elektrons beträgt zum Beispiel 1/2 (in den richtigen Einheiten), der des Protons auch, während Photonen einen Spin von 1 haben.

Innerhalb der handelsüblichen Physik bestimmt der Spin, wie sich zwei Teilchen zueinander verhalten. Teilchen mit einem halbzahligen Spin (Fermionen genannt) können niemals im selben Zustand sein. Zu diesen Teilchen gehören eben Elektronen, Protonen und Neutronen (sowie die Quarks, aus denen die Protonen und Neutronen bestehen). Dieses Verbot desselben Zustands nennt man das Pauli-Prinzip. Teilchen mit ganzzahligem Spin (die heißen Bosonen) dagegen können nicht nur im selben Zustand sein, sie finden das sogar besonders toll (etwas wissenschaftlicher ausgedrückt: Die Wahrscheinlichkeit, Teilchen mit ganzzahligem Spin im selben Zustand zu finden, ist erhöht). Deswegen kann man zum Beispiel Laser bauen – in einem Laserstrahl sind alle Photonen im selben Zustand. (Naja, die Wahrheit ist noch etwas komplizierter, weil die Zahl der Photonen in einem Laserstrahl nicht exakt festliegt.) Dass die Teilchen, aus denen unsere Materie sich zusammensetzt, alle halbzahligen Spin haben, ist auch kein Zufall, wie wir dann gleich beim Spekulieren sehen werden.

Elektronen ohne Spin

Würden wir den Spin von Elektronen und Protonen einfach in der normalen Physik zu Null setzen, dann würden sie zu Bosonen werden. Damit wäre unsere Welt sofort bis zur Unkennntlichkeit verändert. Unsere Chemie beispielsweise würde ohne das Pauli-Prinzip nicht funktionieren. Um das einzusehen, müssen wir kurz einen Blick auf die Energieniveaus der Elektronen in einem Atom werfen. Die Elektronen können nur Zustände mit bestimmter Energie einnehmen (die Energie ist quantisiert, deswegen heißt der entsprechende Zweig der Physik ja auch Quantenmechanik). Es gibt einen günstigsten Zustand (den Grundzustand) und dann viele angeregte Zustände mit höherer Energie. Man kann die Zustände (beim Grundzustand angefangen) durchnummerieren und spricht auch gern von Elektronen”schalen”.

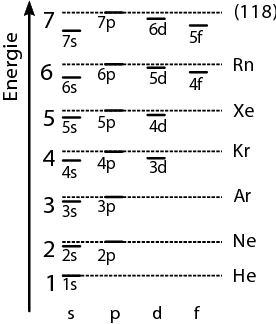
Je höherenergetisch die Schale ist, desto mehr Elektronen finden in ihr Platz. Die erste Schale (der Grundzustand) bietet Platz für zwei Elektronen, die aber unterschiedlichen Spin ahben und sich so am Pauli-Prinzip vorbeimogeln. Die zweite Schale hat 4 mögliche Zustände, und hier passen in jeden 2 Elektronen, macht also 8. Jetzt wird es etwas komplizierter, weil die dritte Schale Platz für 18 Elektronen bietet, aber in einem echten Atom, in dem die niederenergetischen Zustände auch besetzt sind, verschieben sich die Energie dieser Zustände etwas gegeneinander. Es werden deshalb nur 8 Elektronen in der dritten Schale untergebracht (in 4 unterschiedlichen Zuständen, jeweils mit zwei Möglichkeiten für den Spin.), bevor dann Elektronen auf die 4. Schale gehen. Auch in der 4. Schale sind die Energien wieder ein wenig verschoben. Ein Zustand der 4. Schale (mit Platz für zwei Elektronen) hat eine hinreichend kleine Energie, dass er erst einmal besetzt wird. Danach aber sind die noch fehlenden Zustände der 3. Schale dran, die jetzt aufgefüllt werden. Diese kleine Grafik hier (aus einem sehr empfehlenswerten Buch…) veranschaulicht die Energien. Die Zahlen links nummerieren die Schalen durch, die Buchstaben stehen für unterschiedliche Zustände. (Dabei haben s-Zustände Platz für 2 Elektronen, p-Zustände für 6, d-Zustände für 10 usw.) Die Kürzel rechts geben jeweils die Edelgase an, die energetisch besonders günstig sind.

Diese komplizierte Verschiebung der Energieniveaus führt dazu, dass es im Periodensystem Nebengruppenelemente gibt – wenn ihr die Erklärung hier nehmt und ein Periodensystem danebenhaltet, könnt ihr sehen, dass das gut zusammenpasst. (Und wenn ihr es ausführlicher wissen wollt, wisst ihr ja, welches Buch ihr euch noch schnell zu Weihnachten wünschen könnt – Ka-chingg!)

Im Wasserstoff (das einen Atomkern mit nur einem Proton hat) mit einem Elektron ist die erste Schale halbvoll, deswegen geht Wasserstoff gern chemische Bindungen ein. Helium (mit zwei Protonen (und zwei Neutronen) im Atomkern) hat zwei Elektronen auf der innersten Schale (die beiden haben entgegengesetzten Spin und sind deshalb nicht im selben Zustand) – ein drittes hätte dort keinen Platz und muss auf die nächste Schale, die aber energetisch ungünstig ist – und weil ein Helium-Atom mit drei Elektronen auch noch negativ geladen wäre (wegen der zwei Protonen im Kern), ist ein Helium-Atom mit drei Elektronen instabil. Deswegen ist Helium ja auch ein Edelgas.

Ein stabiles Element mit drei Elektronen ist das Lithium – es hat drei Protonen im Kern (mit passenden Neutronen dazu) – aber nicht alle drei zugehörigen Elektronen finden auf der innersten Schale (also im energetisch günstigsten Zustand) Platz – eins der Elektronen muss auf die nächst höhere, energetisch ungünstigere Schale ausweichen. Und so geht es im Periodensystem weiter – je mehr Elektronen ein Element hat, desto höherenergetisch sind die Zustände, die die Elektronen einnehmen müssen.

Wären Elektronen Bosonen, dann könnten sie aber immer alle auf die innerste Elektronenschale, egal wie viele es sind. Chemische Bindungen würde es trotzdem geben können, soweit ich sehe – denn auch beim Wasserstoff ist es ja energetisch günstig, wenn sich zwei Atome die Elektronen teilen. Das liegt letztlich daran, dass sich die Elektronen dann bevorzugt zwischen den Atomen aufhalten können, was energetisch günstig ist, weil sich dort die beiden elektrischen Ladungen der Protonen überlagern. (Ausführlich habe ich das hier erklärt.) Aber wenn wir drei Wasserstoffatome zusammenfügen würden, dann könnten sich die Elektronen über alle drei verteilen, ohne dass – wie in unserer Welt – das Pauliprinzip das verhindert. Und so geht es auch mit 4, 5 oder 1000 Wasserstoffatomen weiter. Wasserstoff wäre damit – wenn ich es mir korrekt überlegt habe – ein Metall. Und das würde auch für jedes andere Element gelten – es wäre immer möglich, die Elektronen einfach gleichmäßig über alle Atome zu verteilen, so dass erst mal alle Elemente metallisch wären.

Das bosonische Metall hätte allerdings deutlich andere Eigenschaften als die Metalle, die wir kennen – beispielsweise wäre seine Wärmekapazität etwa hundert Mal höher als die von normalen Metallen, weil alle Elektronen thermische Energie aufnehmen können. In einem normalen Metall ist das anders, denn die Elektronen besetzen unterschiedliche energetische Zustände, und die meisten von ihnen haben sehr niedrige Energien und können deshalb nur mit sehr großen Energiebeträgen angeregt werden, weil alle Zustände um sie herum besetzt sind (eben wegen des Pauli-Prinzips). (Ach ja, ratet mal, in welchem Buch das erklärt wird…) Auch die elektrische Leitung würde in so einem Metall deutlich anders funktionieren – denn auch hier sind es in unserer Welt nur die Elektronen mit der höchsten Energie, die daran beteiligt sind. In einem bosonischen Metall wären alle Elektronen beteiligt – ich kann allerdings im Moment nicht abschätzen, welche Konsequenz das für die Leitfähigkeit hätte, aber unverändert dürfte sie nicht bleiben. (Sie wird aber nicht einfach um einen Faktor 100 steigen – es sind zwar mehr Elektronen beteiligt, aber die haben kleinere Geschwindigkeiten, weil in unserer Welt das Pauli-Prinzip Elektronen in Zustände mit hoher Geschwindigkeit zwingt. Das bosonische Elektronen-Metall würde sich ein wenig wie das klassische Drude-Modell von Metallen verhalten.)

Allerdings könnte noch etwas anderes passieren: Wenn alle Elektronen Bosonen sind, dann können sie auch bei der elektrischen Leitung alle in denselben Zustand gehen. Zumindest bei halbwegs niedrigen Temperaturen würde damit jedes Metall zum Supraleiter (ohne solche Effekte wie Cooper-Paarbildung zu bemühen.) Leider fehlt mir gerade jede Idee, wie man abschätzen kann, bei welchen Temperaturen das passieren würde.

Bei Atomen mit sehr vielen Elektronen mag noch ein anderer Effekt hinzukommen – die elektrische Abstoßung der Elektronen. Alle Elektronen auf der innersten Schale eines Atoms zusammenzuquetschen, führt natürlich zu relativ großer elektrischer Abstoßung – es mag sein, dass es bei sehr vielen Elektronen doch günstiger wird, einige Elektronen nach Außen zu verdrängen. Auf der anderen Seite ist ein weiter Außen liegendes Elektron weiter vom Atomkern und dessen positiver Ladung entfernt und würde von den innen liegenden Elektronen abgeschirmt werden, was wiederum elektrisch ungünstig ist. Auf Anhieb kann ich nicht sagen, welcher Effekt stärker ist, aber ich vermute, dass die Kernanziehung meist überwiegen wird.

Was mich auf einen weiteren Punkt bringt: Je größer die Kernladung, desto kleiner sind die Elektronenschalen. In unserer Welt sorgt das Wechselspiel aus höherer Kernladung einerseits und höheren besetzten Elektronenschalen andererseits dafür, dass der Durchmesser von Atomen immer zumindest halbwegs in der gleichen Größenordnung liegt – ein Wasserstoffmolekül mit nur einem Elektron hat einen Bindungsabstand von etwa 0,75 Angström (ein Zehntel Nanometer oder ein Zehnmilliardstel Meter), der Bindungsabstand im Gold, das 79 Elektronen hat, die auf 6 Schalen verteilt sind, liegt bei etwa 4 Angström (das ist die Gitterkonstante eines Goldkristalls). Die sechste Schale im Wasserstoffatom liegt wesentlich weiter außen und hat einen Radius von etwa 18 Angström. Durch die höhere Kernladung rücken die Schalen immer dichter an den Atomkern heran, aber weil immer weiter außen liegende Schalen besetzt werden, wird dieser Effekt wieder kompensiert. In unserer Welt mit bosonischen Elektronen wäre das anders – entsprechend gäbe es Atome mit extrem stark unterschiedlicher Größe. Unser metallischer Wasserstoff würde also vermutlich in seinem Inneren Platz für jede Menge Atome mit höherer Ordnungszahl bieten – das gäbe sicher interessante Effekte, macht die bosonische Welt aber noch fremdartiger. (Ich weise noch einmal darauf hin, dass ich mir das alles hier nur selbst zusammengereimt habe – ich übernehme keine Garantie, dass ich nicht irgendeinen wichtigen Effekt übersehen habe.)

Aber bevor ich mir noch weiter Gedanken darüber mache, wie genau die Chemie der Atome unserer bosonischen Welt aussehen würde, sollte ich lieber mal darüber nachdenken, ob es in dieser Welt überhaupt Atome geben würde.

In einem Atomkern gibt es ja Protonen und Neutronen. Und auch die gehorchen dem Pauli-Prinzip. Hat ein Kern viele Protonen und Neutronen, dann können auch die nicht mehr alle in die energetisch günstigsten Zustände. Es gibt ein Schalen-Modell ähnlich wie für Elektronen (das Modell ist aber nicht ganz so gut, weil die Kernkraft stärker und auch noch kurzreichweitig ist). In einem Atomkern mit vielen Protonen (und Neutronen) sind deswegen einige Protonen in energetisch eher ungünstigen Zuständen. Die zugehörigen Schalen sind auch größer – und das führt dazu, dass die Protonen irgendwann über einen so großen Raum verteilt sind, dass die Kernkraft nicht mehr stark genug ist, sie alle zusammenzuhalten. (Das ist jetzt ein sehr schwammiges Bild des ganzen – zum einen, weil das hier ausreicht und es nicht notwendig ist, sich über Aufenthaltswahrscheinlichkeiten usw. detailliert Gedanken zu machen, zum anderen weil ich von Kernphysik keine Ahnung habe…) Deswegen sind Atomkerne mit vielen Protonen auch meist radioaktiv – es ist energetisch günstiger, den Kern in zwei Teile zu teilen, so dass alle Protonen günstigere Zustände einnehmen können und die elektrische Abstoßung zwischen ihnen minimiert wird.

Ohne das Pauli-Prinzip könnten aber aller Protonen (und Neutronen) sehr eng zusammenrücken, weil alle dieselben Zustände einnehmen. Eigentlich gibt es dann keinen Grund mehr, warum sich nicht auch sehr große Atomkerne bilden könnten. Spontan würden sich die Atomkerne nicht direkt miteinander verbinden, weil sie sich dazu erst einmal nahe genug kommen müssten (und das verhindert die elektrische Abstoßung). Wie genau die energetischen Verhältnisse sind, kann ich nicht abschätzen – es ist aber durchaus möglich, dass sich beim Urknall wesentlich mehr schwere Elemente gebildet hätten, als dies in unserem Universum der Fall war.

Wobei – wieso eigentlich Protonen und Neutronen? Die bestehen ja jeweils aus drei kleineren Teilchen, den Quarks. Die Quarks sind dabei nie im selben Zustand, weil sie unterschiedliche “Farbladungen” tragen (was ein blöder Name für die Ladung ist, die eben für die starke Kernkraft zuständig ist). Ohne Pauli-Prinzip sollte es aber eigentlich möglich sein, auch mehr Quarks zu einem Verbund zusammenzuschließen – ich sehe im Moment nicht, was dagegen sprechen sollte. Dann gäbe es keine Protonen und Neutronen sondern Agglomerate von Quarks mit unterschiedlicher Größe – und hier hört jetzt meine Kenntnis der starken Kernkraft (und vielleicht auch meine Fantasie) auf. Würden sich dann gigantische superdichte und schwere Ansammlungen von Quarks bilden, so ähnlich wie Neutronensterne? Ich vermute schon – dann würde die Welt vermutlich aber sehr langweilig werden, denn das Universum wäre dann im wesentlichen angefüllt mit Quarksternen und schwarzen Löchern (wenn die Quarksterne zu groß werden).

Eine Welt ganz ohne Pauli-Prinzip ist in jeder Hinsicht so weit von unserer entfernt, dass es schwer ist, sie sich vorzustellen.

Elektronen mit Pauli-Prinzip, aber ohne Spin

Aber da es eh nur ein Gedankenexperiment ist, können wir uns ja auch vorstellen, dass die Elektronen und sonstigen Fermionen in unserer spinlosen Welt trotzdem dem Pauli-Prinzip gehorchen. Es dürfen also nie zwei Elektronen im selben Zustand sein – aber jetzt können sie sich eben nicht mehr dadurch rausmogeln, dass sie unterschiedliche Spins haben. Unsere Elektronen (und Quarks, Protonen usw) gehorchen also trotz Spin 0 dem Pauli-Prinzip.

Ich sage gleich dazu, dass so eine Welt gar nicht konsistent möglich ist – fügt man die Regeln der Relativitätstheorie und der Quantenmechanik zusammen, dass folgt daraus zwingend, dass Teilchen mit Spin Null Bosonen sein müssen. (Für dieses sogenannte Spin-Statistik-Theorem gibt es keine wirklich gute anschauliche Erklärung – nicht mal die von Feynman in den Dirac memorial Lectures ist so richtig toll. Falls jemand eine gute Erklärung kennt…?) Eine Weilt, in der Elektronen dem Pauli-Prinzip gehorchen, aber Spin 0 haben, wäre also auch eine Welt, in der entweder die Quantenmechanik oder die Relativitätstheorie nicht gilt, und damit von der uns bekannten Physik so weit entfernt, dass man die Konsequenzen vermutlich nicht sinnvoll abschätzen kann. Aber egal – das hier ist ein Blog, kein wissenschaftliches Buch, und ich kann mir die Regeln hier so machen, wie es mir passt.

Also nehmen wir einfach mal an, alle Fermionen (wie Quarks, Protonen usw) würden dem Pauli-Prinzip gehorchen, hätten aber trotzdem Spin Null. Um diese Welt von der eben zu unterscheiden, nenne ich sie die Spin-0-Welt. In gewisser Weise ist das das andere Extrem – in unserer Welt passen zwei Teilchen (mit unterschiedlichem Spin) in einen Zustand, in der bosonischen Welt beliebig viele, aber in der Spin-0-Welt nur noch eins.

Zumindest Protonen und Neutronen würde es trotzdem geben können – anders als eben. Denn hier tun sich drei Quarks mit unterschiedlicher “Farbladung” zusammen, das Pauli-Prinzip ist also auch ohne Spin erfüllt.

Bei den Atomkernen wird es allerdings schon schwieriger. Helium ist in unserer Welt ein energetisch besonders günstiger Kern, weil hier beide Protonen (und beide Neutronen) jeweils die innere “Schale” des Kerns besetzen. In unserer Spin-0-Welt wäre das anders – die Bindungsenergie von zwei Protonen und zwei Neutronen wäre deutlich geringer. Und das macht schon gleich vom Start weg Probleme, denn Atome mit größeren Kernen entstehen ja schrittweise in Sternen – und dazu müssen diese Zwischenstufen (beispielsweise Helium-3) eben energetisch günstiger sein. Ob Atome jenseits des Wasserstoffs in der Spin-0-Welt überhaupt entstehen würden, ist also fraglich. Auf jeden Fall sieht es für sehr große Atome schlecht aus – verabschiedet euch besser vom Gold, denn Atomkerne mit 79 Protonen wären vermutlich so radioaktiv, wie es in unserer Welt Kerne mit weit über 100 Protonen sind.

Aber selbst wenn es Atome gäbe, dürfte auch die Chemie der Spin-0-Welt uns sehr fremd sein. Wasserstoff ist in unserer Welt ein Tausendsassa, der mit fast allem Verbindungen eingehen kann und der besondere Tricks auf Lager hat, weil ein positives Wasserstoff-Ion nur ein winziges Proton ist. In der Spin-0-Welt ist aber die innere Elektronenschale des Wasserstoff mit einem Elektron bereits voll – Wasserstoff ist also ein Edelgas.

Im Helium haben wir dann ein Elektron auf der innersten und eins auf der zweiten Schale. Damit wäre jetzt Helium ein Metall, denn es fehlen ihm noch 3 weitere Elektronen, um die zweite Schale voll zu machen. (In unserer Welt hat die zweite Schale ja Platz für 8 Elektronen, in der Spin-0-Welt also nur für 4.) Das nächste Element wäre dann Lithium – mit zwei Elektronen auf der zweiten Schale fehlen ihm nur noch zwei, um energetisch günstig angeordnet zu sein. Zwei Lithiumatome würden also (so wie bei uns der Sauerstoff) eine Doppelbindung eingehen und wären damit energetisch zufrieden. Danach kommt Bor – dem fehlt nur noch ein Elektron auf der äußeren Schale, so dass es sich eher wie Fluor verhalten würde; chemisch ziemlich aggressiv, um eine energetisch günstige Konfiguration zu bekommen. Tja, und ein Element wie Kohlenstoff, das bis zu vier Bindungen eingehen kann, suchen wir in unserer Spin-0-Welt vergeblich. Auch Halbleiter dürfte es nicht geben – Stoffe sind entweder Metalle (wenn sie ein Elektron auf der äußersten Schale haben wie Lithium) oder Gase. Zusätzlich wären all diese Atome deutlich größer als in unserer Welt, weil ein Atom, bei dem die äußersten Elektronen auf zum Beispiel der zweiten Schale sitzen, eben weniger Protonen im Kern hat, so dass die Anziehung an den Kern schwächer ist.

Weiter unten im Periodensystem gibt es dann auch entsprechend weniger Nebengruppenelemente (das sind die, bei denen energetisch ungünstige innere Elektronenschalen aufgefüllt wären). Vermutlich würden sich hier einige Bindungsverhältnisse verschieben (weil Effekte wie die Wechselwirkung zwischen dem Elektronenspin und dem magnetischen Moment des Atomkerns verschwinden) – welche Effekte das hätte sehe ich aber gerade nicht.

Ach so – Magnetismus. Den üblichen Ferromagnetismus (also Materialien wie Eisen, das magnetisierbar ist) gibt es in unserer Spin-0-Welt nicht, denn der Effekt kommt allein dadurch  zu Stande, dass im Eisen mehr Elektronen den einen Spin als den anderen haben. Andere magnetische Effekte kann es immerhin noch geben, weil Elektronen auf Bahnen um den Atomkern einen Bahndrehimpuls haben, der auch magnetische Effekte hervorruft.

Die Spin-0-Welt ist vielleicht etwas dichter an unserer Welt dran als die bosonische Welt – immerhin gibt es in ihr Atome (falls sie denn entstehen können) und eine rudimentäre Chemie. Leben wie wir es kennen, wäre aber sicherlich nicht möglich und die Spin-0-Welt wäre schon ziemlich fremdartig (und vermutlich auch ziemlich langweilig).

Auch wenn Dinge wie das Pauli-Prinzip und der Spin von Teilchen also sehr abstrakte Konzepte der theoretischen Physik sind – ohne sie gäbe es uns nicht.