Die Quantenmechanik ist ja immer für scheinbar verrückte und der Intuition widersprechende Tricks gut. Einer der neuesten (naja, so neu auch nicht, das paper ist vom letzten August, Dank übrigens an Alderamin) besteht darin, ein Objekt zu fotografieren, ohne das Licht, das auf das Objekt fällt, überhaupt zu messen.
Das klingt natürlich völlig absurd – klappt aber trotzdem. Hier erst mal die stichwortartige Kurzerklärung: Der Trick beruht darauf, dass man das Licht (oder genauer gesagt, das Photon), das auf das Objekt fällt, mit einem anderen Photon verschränkt. (Verschränkung ist der quantenmechanische Kniff, bei dem man dafür sorgt, dass Veränderungen an einem Objekt sich an einem anderen zumindest indirekt bemerkbar machen. Ausführlich erklärt im dritten Teil meiner “Quantenmechanik-Verstehen-Serie”, eine kurze Erklärung findet ihr auch in diesem Text über Vögel, die den Trick auch drauf haben.) Je nachdem, ob das erste Photon mit dem Objekt wechselwirkt oder nicht, ändert sich der gemeinsame Zustand, und das kann man dann mit Hilfe des zweiten Photons herausbekommen. Man lässt also ein Photon mit dem Objekt wechselwirken, misst aber hinterher ein anderes. Nett dabei ist, dass die beiden Photonen unterschiedliche Wellenlängen haben können – prinzipiell kann man auf diese Weise ein Objekt mit Photonen fotografieren, für die man gar keinen Detektor hat, der diese Photonen messen kann.
So, das war die Kurzfassung, sozusagen die “Wie erkläre ich es in einer Minute auf einer Party”-Version. Aber wenn ihr glaubt, dass der Artikel jetzt damit zu Ende ist, dann kennt ihr meinen Blog nicht. Um zu erklären, wie das ganze genau funktioniert, hole ich etwas aus. (Ich habe selbst auch eine Weile und etwas Nachhilfe vom physicsforum gebraucht, weil in der Nature-Fassung des Papers leider ein entscheidender Satz der Kürzung zum Opfer viel und ich erst mal in eine völlig falsche Richtung gedacht habe.) Wie üblich beschränke ich mich auf die Prinzipien – der technische Umsetzungskrams ist nix für mich.
Um das Prinzip zu verstehen, schauen wir erst mal ein inzwischen schon fast “klassisches” Experiment an, den quantenmechanischen (ab jetzt wie üblich qm abgekürzt) Bombentester:

„Elizur-Vaidman – Experimental Setup – default“. Lizenziert unter Gemeinfrei über Wikimedia Commons.
Dieses schicke Gerät funktioniert so: Links unten wird ein Photon erzeugt, das dann auf einen halbdurchlässigen Spiegel trifft. (Das bedeutet, dass das Photon mit einer Wahrscheinlichkeit von 50% durch den Spiegel nach rechts durchgeht und mit einer Wahrscheinlichkeit von 50% nach oben im Bild reflektiert wird.) Das Photon kann jetzt also entweder erst nach rechts und dann nach oben laufen oder erst nach oben und dann nach rechts. (Die Spiegel an den Ecken links oben und rechts unten sind ganz normale Spiegel, die das Photon einfach reflektieren.) Oben rechts ist dann wieder ein halbdurchlässiger Spiegel, so dass das Licht entweder durchgeht oder reflektiert wird.
Stellt man sich das Photon als ein gewöhnliches Teilchen in der klassischen Physik vor, dann gibt es vier Möglichkeiten, je nachdem, was an den beiden halbdurchlässigen Spiegeln passiert: Durchgelassen-durchgelassen, dann landet das Photon im oberen Detektor (das orangene Dings), durchgelassen-reflektiert, so dass das Photon im Detektor rechts landet, oder reflektiert-durchgelassen-Reflektor rechts oder reflektiert-reflektiert – Detektor Oben. Bei einem klassischen Teilchen würden wir also erwarten, dass wir die Hälfte der Teilchen rechts und die Hälfte oben wiederfinden.
Als nächstes betrachten wir das Licht als elektromagnetische Welle – dann wird die Welle an jedem halbdurchlässigen Spiegel in zwei Teilwellen aufgespalten, und am Ende interferieren die beiden Wellen miteinander. Dabei wird der Teil, der im Bild nach oben geht, ausgelöscht, weil die beiden Wellen auf diesem Weg unterschiedlich oft reflektiert werden und die Lichtwelle beim reflektieren ein wenig verschoben wird – das ist die destruktive Interferenz, bei der sich zwei Wellen so überlagern, dass sie sich auslöschen können. Licht landet deshalb nur im Detektor rechts. (Die genaue Abzählerei der Phasenverschiebungen können wir uns hier sparen, es geht nur ums Prinzip.)
Jetzt drehen wir das Licht immer schwächer, bis zu jedem Zeitpunkt nur noch ein einzelnes Photon von der Lichtquelle ausgesandt wird. Obwohl man sich das Photon gern als Teilchen vorstellt, bleibt der Interferenz-Effekt erhalten: Das Photon landet immer im Detektor rechts, wie oben im Bild.
Anschaulich sagt man auch gern: “Das Photon geht beide Wege gleichzeitig und interferiert dann mit sich selbst”.
Jetzt nehmen wir den selben Aufbau und bauen ein Hindernis (in diesem Bild etwas schwer zu erkennen, ein blasser Kreis oben in der Mitte) in einen der Lichtwege ein:
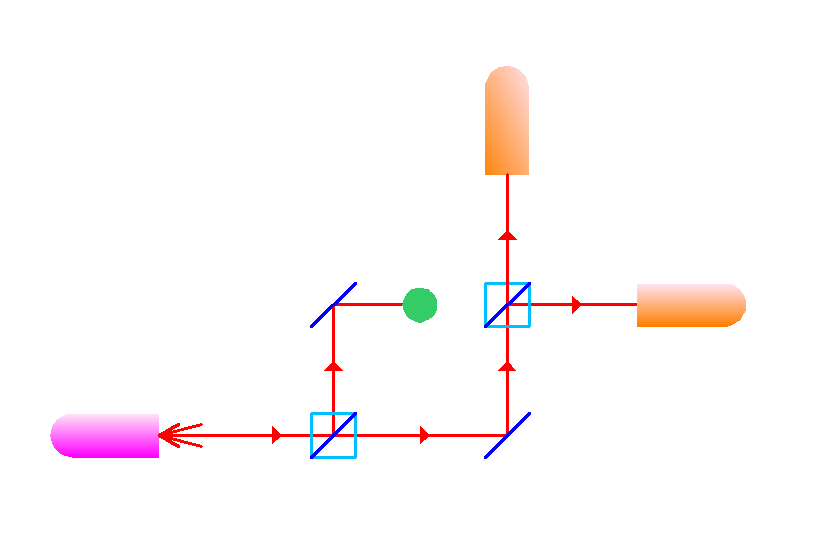
„Elitzur-Vaidman – Experimental Setup with object“ von MovGP0 – https://commons.wikimedia.org/wiki/File:Elizur-Vaidman_-_Experimental_Setup_-_with_object.png. Lizenziert unter CC0 über Wikimedia Commons.
Wenn das Photon jetzt den oberen Weg geht, dann wird es dort absorbiert. In 50% aller Fälle bekommen wir also gar kein Licht in unseren beiden Detektoren. In den anderen 50% der Fälle bekommen wir Licht – entweder rechts, wenn das Photon am halbdurchlässigen Spiegel reflektiert wurde, oder oben, wenn es nicht reflektiert wurde.
Und das ist der Clou bei diesem Aufbau: stellt euch vor, ihr wisst nicht, ob ein Objekt im Strahlengang oben ist oder nicht. Wenn ihr ein Photon im oberen Detektor findet, dann wisst ihr, dass ein Objekt da war, obwohl das Photon den Weg gar nicht gegangen ist und entsprechend auch nicht mit dem Objekt wechselwirken konnte. Um das noch augenfälliger zu machen, nimmt man gern an, dass es sich bei dem Objekt um eine Bombe handelt, die sofort explodiert, sobald ein Photon auftrifft: Im 50% aller Fälle sieht es schlecht aus für euer Labor, weil die Bombe explodiert, in 25% der Fälle landet ein Photon rechts im Detektor, und ihr wisst nicht, ob die bombe da ist oder nicht, aber in immerhin 25% der Fälle könnt ihr feststellen, dass die Bombe da ist, ohne sie zu zünden. (Mit einem komplizierteren Aufbau kann man die Erfolgsquote des Detektors auch deutlich vergrößern und sie beliebig dicht an den Wert 1 bringen, so dass es sehr unwahrscheinlich wird, dass die Bombe explodiert – ganz unmöglich ist es bei diesem Versuch aber nie.)
Statt eine Bombe zu detektieren, könnt ihr mit dem Aufbau auch ein Bild aufnehmen – nehmt an, ihr wollt einen Schattenriss eines Objektes erzeugen, dann könnt ihr das Objekt im Strahlengang hin und her bewegen und jeweils für jede Position sehen, ob ihr Photonen im oberen Detektor bekommt (dann ist das Objekt im Strahlengang) oder nicht.
Dieser Aufbau ist auch schon einer der Tricks in der neuen Quantenkamera – aber wenn das alles wäre, dann wäre es vermutlich kein Nature-Paper wert gewesen. Das ganze wurde nämlich noch im eine Stufe verkompliziert – die Photonen, die mit dem Objekt wechselwirken (oder auch nicht) werden nämlich gleich weggeworfen und gar nicht betrachtet.
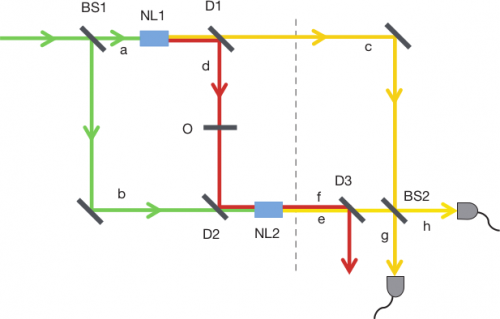
Hier ein vereinfachtes Schema des Versuchsaufbaus (nicht erschrecken, es sieht etwas komplizierter aus als der Bombentester):
Aus Lemos et al., s.u.
Das einfallende Photon kommt von links oben und trifft auf den halbdurchlässigen Spiegel (BS steht hier für “beam splitter”, nicht für Braunschweig und auch nicht für das, was ihr gerade dachtet…). Wenn ihr für einen Moment das ganze Gedöns ignoriert, dann seht ihr, dass der Strahl zwei Wege gehen kann, entweder oben herum bei NL1 und D1, hin zum Spiegel und dann nach unten, oder unten herum, über den Spiegel, vorbei an D2, NL2 und D3. Insofern ist der Aufbau ähnlich wie beim Bombentester.
Aber auch nur so ähnlich. Denn natürlich passiert da noch ein bisschen mehr. Schauen wir erst mal auf den oberen Weg: Dort trifft der grüne Strahl auf NL1. Das ist ein “nicht-linearer Kristall” – ein spezielles Material in der Optik, das eine sehr interessante Eigenschaft hat: Es macht aus einem Photon zwei. Wie das funktioniert, wäre vermutlich einen eigenen Blog-Eintrag wert (dazu müsste ich es aber selbst erst mal ganz genau verstehen…). Ich setze mal gerade meinen Ingenieurs-Hut auf und frage nicht, wie das genau geht, sondern nur, was es macht. Und das ist recht simpel: Das einfallende Photon (aus einem grünen Laser) wird in zwei Photonen konvertiert, nämlich eins im roten (im Bild gelb) und eins im infraroten (im Bild rot) Bereich. Die beiden Photonen haben zusammen genau die Energie des einfallenden Photons und sie sind miteinander quantenmechanisch verschränkt, weil sie ja gleichzeitig erzeugt wurden und man das eine nur mit dem anderen zusammen bekommt.
Diese beiden Photonen fallen jetzt auf D1 – das ist ein spezieller Spiegel, der das infrarote Photon reflektiert, aber das andere durchlässt. Das infrarote Photon fällt jetzt auf das Objekt O, das abgebildet werden soll (wir wollen also am Ende wissen, ob das Objekt O da ist oder nicht, genau wie beim Bombentester). Nehmen wir erst mal an, das Photon passiert das Objekt O ohne jede Beeinflussung. Dann läuft es weiter nach unten, trifft auf D2 (noch so ein Spezialspiegel), wo es reflektiert wird, und läuft dann durch den nicht-linearen Kristall N2, der für dieses Photon aber durchsichtig ist und mit ihm nichts anstellt. An D3 wird es dann reflektiert und darf gegen die Laborwand leuchten oder sonst wo absorbiert werden – sein weiteres Schicksal interessiert uns nicht.
Als nächstes schauen wir auf den zweiten Weg: Das Photon links oben wird also nach unten abgelenkt, nach rechts reflektiert, und trifft dann auf NL2. Dort wird dieses Photon dann ebenso in ein rotes (im Bild gelb) und ein infrarotes (im Bild rot) konvertiert. Hmm, das mit den Farben ist verwirrend, ich glaube, ich mache es ab jetzt so wie im paper auch: Das rote Photon (im Bild gelb) bezeichne ich als “Signal”, weil es hinterher detektiert werden soll, das infrarote als “idler” (weil uns das nicht interessiert, besonders faul ist es aber eigentlich nicht.).
Also: das grüne photon trifft auf NL2 und produziert dort ein Signalphoton (gelb) und ein idler-Photon (rot). Falls ihr euch jetzt wundert, warum dann hinter NL2 nicht zwei rote idler sind, nämlich eins von oben, das in NL1 erzeugt wurde, und eins von links, erzeugt in NL2: Die Intensität des Lasers und die Effizienz der nichtlinearen Kristalle sind niedrig genug, dass es sehr unwahrscheinlich ist, dass in beiden Kristallen eine Konversion stattfindet – ähnlich wie im Bomben-Detektor, wo wir ja auch immer nur ein Photon hatten, das aber irgendwie beide Wege geht. (Diese wichtige Sicherheitsinformation steht übrigens nicht im paper, wohl aber in der arXiV-Version; ist wohl dem nature-Kürzungs-Teufel zum Opfer gefallen. Hat mich wie gesagt ziemlich verwirrt.) So, das grüne Photon erzeugt also auf diesem Weg in NL2 einen idler und ein Signal.
Solange bei O nichts passiert, haben wir jetzt erst einmal eine ähnliche Anordnung wie beim ersten Bild ganz oben (dem Bombentester ohne Hindernis). Das Photon kann zwei Wege gehen, auf jedem der Wege erzeugt es ein Signalphoton, und das interferiert am Ende (bei BS2) mit sich selbst, so dass es entweder beim Detektor bei g oder bei h landet. Die Sache ist nur dadurch verkompliziert, dass wir das Photon unterwegs jeweils von grün in den Signal-Zustand konvertieren und zusätzlich noch einen idler erzeugen. Entscheidend für den Aufbau ist, dass wird dem idler hinter NL2 nicht ansehen können, durch welchen der beiden Prozesse er entstanden ist. Könnten wir das in irgendeiner Weise tun, dann könnten wir (durch einen Detektor hinter D3) herausfinden, ob das Photon nun oben oder unten herum gelaufen ist. Das würde die Interferenz zerstören.
Wenn wir jetzt ein Hindernis bei O einbauen, dann wird es komplizierter. Nehmen wir an, dass das Hindernis das idler-Photon mit Sicherheit absorbiert. Dann haben wir nur zwei Möglichkeiten: Entweder das Photon geht oben herum (bei c), dann haben wir keinen idler bei f, oder das Photon geht unten herum und wir haben einen idler bei f. Jetzt könnten wir diese beiden Zustände prinzipiell unterscheiden, indem wir den idler messen – damit gibt es keine Intereferenz mehr. Entweder trifft also ein Photon von oben auf BS2, oder von links. In beiden Fällen ist die Wahrscheinlichkeit dafür, ein Photon bei g oder h zu messen, jeweils 50%.
Falls das Objekt bei O das Photon aber immer durchlässt, können die beiden Photonen c und e miteinander interferieren, denn jetzt können wir nicht mehr durch messen des idlers herausfinden, was von beiden passiert ist. Im Experiment wird der idler nicht analysiert – aber der trifft ja z.B. auf die Laborwand und hinterlässt dort Energie; auch wenn wir ihn nicht wirklich messen, könnten wir das tun, also sind die Zustände unterscheidbar. Das ist ähnlich wie im klassischen Doppelspalt-Experiment (siehe auch hier für ein schickes Video dazu) – wenn man misst, welchen Weg das Elektron geht, dann wird die Interferenz zerstört. In diesem Fall, wenn also der idler bei O durchgelassen wird, können die beiden Photonen bei BS2 interferieren, und genau wie im Bombendetektor ohne Hindernis finden wir dann das Photon immer nur in einem Detektor und nie im anderen. (Hmm, eigentlich würde ich erwarten, dass man das Photon in dem Fall immer bei h findet, so wie beim Bombendetektor oben – im paper steht aber das Gegenteil. Vermutlich findet an irgend einer Stelle noch eine Phasenverschiebung statt; für’s Prinzip ist es aber auf jeden Fall egal.)
Wir können also fleißig Licht einstrahlen und auf unsere Detektoren schauen. Wenn wir etwa gleich viele Photonen in beiden finden, dann ist bei O ein Hindernis, sonst nicht. (Das paper analysiert den allgemeinen Fall, wo das Hindernis nur eine Wahrscheinlichkeit hat, das Photon zu absorbieren und zusätzlich noch phasenzuverschieben, aber das macht die Sache zwar komplizierter, ändert am nichts am Prinzip.) Das Tolle an dem Aufbau ist, dass wir die photonen, die bei O mit dem Objekt wechselwirken, gar nicht messen. Wenn wir also einen Detektor haben, der infrarote Photonen nicht detektieren kann, können wir trotzdem das Objekt bei O mit infrarotem Licht abbilden.
Um aus dem ganzen jetzt eine echte Kamera zu machen, muss man natürlich noch ein paar Linsen einbauen, damit man ein ganzes Objekt abbilden kann, nicht nur einen Bildpunkt. Das sind aber ja eher technische Probleme – ich setze mal schnell meinen “Theoretischer-Physiker-Hut” auf und erkläre die für uninteressant, es geht ja nur ums Prinzip.
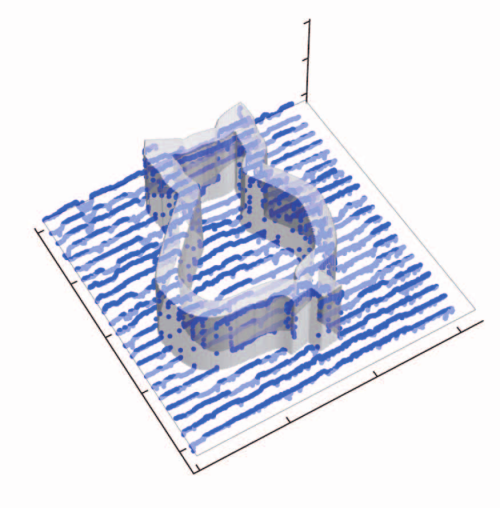
Um das ganze zu testen, wurden verschiedene Objekte in den Strahl bei O gehalten. Ich zeige hier nur ein Bild. Dabei wurde eine Silizium-Platte genommen, die für die Signal-Photonen undurchsichtig ist (sichtbares Licht wird von Silizium absorbiert), für infrarote Photonen aber durchsichtig (das liegt daran, dass Silizium ein Halbleiter ist – Photonen mit zu kleiner Energie können nicht absorbiert werden, weil es keine passenden energetischen Zustände gibt. Das erkläre ich übrigens detailliert ganz woanders.) In diese Platte wurde eine Kontur hineingeätzt:
Aus Lemos et al., s.u.
Weil die Photonen, die durch die Platte hindurchgehen, dabei ein wenig beeinflusst werden (hier kommt jetzt die oben eingeklammerte Phasenverschiebung ins Spiel, die dafür sorgt, dass die Interferenz bei BS2 zusätzlich beeinflusst wird; letztlich liegt es einfach daran, dass Licht in Sulizium langsamer läuft), kann man die eingeätzte Struktur abbilden. So sieht das dann aus:
Aus Lemos et al., s.u.
Die beiden Teilbilder zeigen jeweils, was man am einen und am anderen Detektor sieht, die Helligkeit gibt an, wie viele Photonen detektiert wurden.
Wir beleuchten also das Objekt mit Photonen, die wir nie detektieren (und für die der Detektor auch gar nicht sensitiv ist) und detektieren hinterher Photonen, die von unserem durchstrahlten Objekt vollkommen absorbiert werden würden, wenn sie denn mit ihm Kontakt gehabt hätten. Schon eine ziemlich abgefahrene Anwendung der Quantenmechanik. Wie gesagt, ist das ganze nicht nur eine nette Demonstration der QM, sondern könnte auch praktische Anwendungen haben, weil man auf diese Weise Objekte prinzipiell mit Licht in einem Wellenlängenbereich abbilden kann, für den man keine passenden Detektoren hat.
Lemos, Gabriela B., et al. “Quantum Imaging with Undetected Photons.” arXiv preprint arXiv:1401.4318 (2014).







Kommentare (70)