Wer fleißig diesen Blog liest, wird über die Titelfrage nur den Kopf schütteln – natürlich ist die Raumzeit gekrümmt, dazu gab es hier ja schon diverse Artikel einschließlich einer langen Serie (falls ihr diesen Blog nicht so fleißig lest (das solltet ihr aber!)) findet ihr die meisten Artikel auch rechts mit Hilfe der tag-Wolke). Dass die Raumzeit gekrümmt ist und dass diese Krümmung für das sorgt, was wir im Alltag “Schwerkraft” nennen, ist schließlich die zentrale Aussage der Allgemeinen Relativitätstheorie (kurz ART) – so steht es nicht nur hier im Blog, sondern auch sonst so ziemlich überall. Insofern scheint die Frage ziemlich überflüssig.
Und – wenig überraschend – ich werde die ART in diesem Artikel auch nicht widerlegen. Aber trotzdem werfe ich heute noch einmal einen Blick auf die Raumzeitkrümmung und die Frage, was genau es eigentlich bedeutet, dass die Raumzeit gekrümmt ist. (Fleißige Leserinnen* des Blogs kennen die meisten Argumente schon von hier oder hier – ich schreibe den Artikel trotzdem aus zwei Gründen: Zum einen hilft es – zumindest mir – bei der Anschauung, wenn man Dinge immer wieder leicht verändert durchdenkt, um ein Gefühl zu bekommen (und ein paar Dinge habe ich tatsächlich jetzt besser verstanden als noch vor ein paar Monaten), zum anderen soll der Artikel als Vorbereitung dazu dienen, damit ich demnächst einen Artikel schreiben kann, den ich schon seit Jahren schreiben will (aber aus Gründen der Spannung sage ich noch nicht, worum es da gehen wird, wer die typischen Blogthemen überdebkt, sollte es sich aber überlegen können).)
*Ja, es gibt auch in diesem Artikel ein “generisches” Femininum – alle, die sich darüber aufregen wollen, folgen bitte diesem Link.
Wie so oft hilft es der Anschauung auf die Sprünge, wenn wir die Welt erst mal einfacher machen und so tun, als wäre sie zweidimensional (im Moment rede ich erstmal nur über Raumdimensionen). Stellt euch also vor, ihr wärt ein niedliches kleines zweidimensionales Wesen und würdet auf einer gigantischen Ebene leben.
Ihr könnt also auf dieser Ebene herumkriechen und euch die Welt angucken. Was ihr nicht wisst, ist, dass eure Ebene eine seltsame Eigenschaft hat: Je nachdem, wo ihr euch gerade aufhalten, werdet ihr etwas größer oder kleiner. Wir können uns (wie in diesem Artikel hier, wo ich ein sehr ähnliches Bild verwendet habe) beispielsweise vorstellen, dass es auf eurer Ebene an unterschiedlichen Punkten unterschiedlich warm ist – deshalb dehnt ihr euch da, wo es warm ist, aus und schrumpft da, wo es kalt ist, zusammen. So etwa könnte das aussehen (wobei ihr in Wahrheit natürlich viel viel kleiner seid, so dass für euch an jedem Punkt die Temperatur für alle praktischen Zwecke konstant ist) – hohe Temperaturen sind gelb-orange, niedrige sind blau:
Wie gesagt, ihr wisst davon nichts. Wenn ihr von einem Ort zum anderen reist, dann ist die Veränderung so klein, dass ihr davon nichts merkt. Ihr könntet etwas merken, wenn ihr einen Maßstab hättet, der nicht mitschrumpft oder -wächst. Ihr könntet es auch merken, wenn ihr zum Beispiel ein Lichtsignal hättet, das von der Temperatur nicht beeinflusst wird (dann könntet ihr zum Beispiel messen, wie lang das Lichtsignal braucht, um von eurer Ost- zu eurer West-Seite zu laufen) – aber wir stellen uns vor, dass es bei euch einfach kein Licht gibt. (Hinweis: Wir fragen auch nicht, was genau an den Kanten des Bildes passiert – das spielt hier erst mal keine Rolle.)
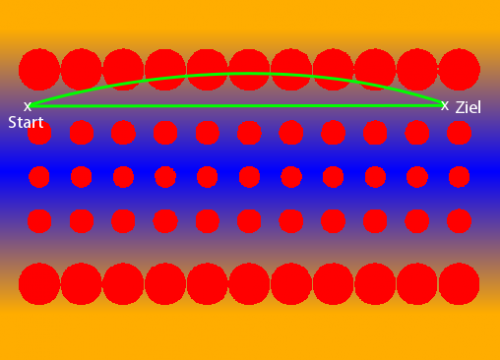
Stellt euch jetzt vor, ihr wolltet von einem Punkt eurer Welt zu einem anderen weit entfernten Punkt reisen, beispielsweise so:
Natürlich habt ihr keine Lust, weiter zu kriechen als unbedingt notwendig. Was ist also der kürzeste Weg vom Start zum Ziel? Normalerweise ist der kürzeste Weg zwischen zwei Punkten bekanntlich eine Gerade:
Ihr könnt aber tatsächlich ein Stück des Weges sparen, wenn ihr auf eurer Route ein Stück weiter nördlich lauft, dann werdet ihr dort ja größer – entsprechend müsst ihr weniger Schritte machen (falls kleine zweidimensionale Kreiswesen schreiten können). Es wäre deshalb klüger, ihr würdet etwa diesen Weg hier gehen:
Damit keine Missverständnisse aufkommen: Ihr wisst ja nichts davon, dass eure Welt so ein seltsames Temperaturfeld hat, das alles verzerrt. Für euch ist dieser Weg eine Gerade, weil es der kürzeste Weg zwischen Start und Ziel ist (auch wenn jemand, der von Außen auf eure Welt guckt, das anders sieht). Von dem seltsamen Temperaturfeld, das alle Maßstäbe verzerrt, wisst ihr nichts.
Für euch sieht eure Welt anders aus – auf ihr gibt es vielleicht Meere oder Felder oder Wälder (ich wollte gerade “Berge” schreiben, aber zweidimensionale Berge sind nicht so leicht vorstellbar (wir kommen aber noch drauf…); eure Meere müssen auch irgendwie vorm Auslaufen geschützt werden, aber über solche Details mache ich mir keine Sorgen (das ist ja das Vorrecht theoretischer Physikerinnen). Eine einigermaßen detailliert ausgearbeitete 2D-Welt findet ihr in diesem Roman beschrieben.)
Machen wir eure Welt also ein wenig hübsch und stellen wir sie uns so vor:

Bild von Stefan Kühn (Eigenes Werk), CC-BY-SA-3.0 oder CC BY-SA 2.5-2.0-1.0 via Wikimedia Commons
Hier seht ihr die unterschiedlichen Länder und Meere eurer Welt und ihr seht auch, wie sich eure Größe verändert, je nachdem, wo ihr gerade seid.
Natürlich dürfte euch das Bild oben bekannt vorkommen – es ist die übliche Mercator-Projektion der Erde, die meist für Karten verwendet wird. Diese Kartenprojektion hat den Vorteil, dass sie winkeltreu ist – das bedeutet, dass ihr auf der Karte bei Objekten (wie beispielsweise Ländern) Winkel ausmessen könnt und diese auch genau den tatsächlichen Winkeln auf der Erdoberfläche entsprechen.
Unsere Erdoberfläche ist aber bekanntlich keine heiße Platte, bei der man an verschiedenen Orten schrumpft oder wächst, sondern sie ist die Oberfläche einer Kugel. So sieht sie eigentlich aus (wobei wieder die gleichen Kreise eingezeichnet sind, die für unsere 2-dimensionalen Wesen stehen):

von Stefan Kühn (Eigenes Werk), CC-BY-SA-3.0 oder CC BY-SA 2.5-2.0-1.0 via Wikimedia Commons
Wenn ihr tatsächlich ein zweidimensionales Kreiswesen seid, dann gibt es für euch keine Möglichkeit, die Situation auf der Kugeloberfläche von der mit der Ebene mit Temperatur irgendwie zu unterscheiden. Dass wir das können liegt daran, dass wir dreidimensional sind und die Erde von Außen vermessen können – historisch war es ja genau so, dass die Beobachtung von Schiffen am Horizont, bei denen man zuerst die Masten sieht, die Krümmung der Erdoberfläche nahegelegt haben. Licht folgt eben nicht der Erdoberfläche.
Ihr könnt jetzt einwenden, dass ihr den Unterschied aber daran bemerken könnt, dass ihr bei einer Kugel einmal wie einst Magellan um die Welt herumsegeln könnt. Das ist auch richtig, aber das geht eben nur dann, wenn eure Kugel klein genug ist, dass das geht. Die Ebene mit Temperaturfeld oder die Kugeloberfläche sollen aber ja den gesamten Raum darstellen, in dem wir leben, also das ganze Universum. Da können wir nicht mal eben schnell einmal drum herumsegeln (zumal sich das Weltall ja auch noch ausdehnt). (Selbst dann könten wir prinzipiell die Weltkarte immer noch zu einem Zylinder aufrollen und dann zumindest von Ost nach West drum herumsegeln; der Nordpol ist allerdings etwas kniffliger.)
Eure zweidimensionale Welt ist im Moment ja noch ganz gleichmäßig gekrümmt (auch wenn wir das der Ebene mit dem Temperaturfeld oben nicht wirklich ansehen). Wir können aber natürlich prinzipiell auch lokale Änderungen der Temperatur zulassen. Wenn es in einem Bereich zum Beispiel kälter ist als in der Umgebung, dann schrumpft dort lokal alles zusammen, so dass der gerade Weg durch diesen Bereich länger ist als ein Weg drum herum erwarten lässt. Im Bild unserer Kugel ist das gerade ein Berg – der Weg über einen Berg ist eben länger als der gerade Weg, der mitten durch den Berg hindurchführen würde. (Jetzt haben wir also doch noch Berge eingebaut – wobei die Berge allerdings genausogut auch Täler sein können, das lässt sich auf diese Weise erst einmal nicht unterscheiden.)
Damit können wir das Bild der Raumkrümmung jetzt auf unser Universum übertragen: Das Universum als ganzes kann eine Krümmung haben, so wie die Erdoberfläche (oder die Ebene). Zusätzlich gibt es auch noch lokal Bereiche mit unterschiedlicher Krümmung. Wir können uns den Raum als gekrümmt vorstellen – wir können aber genauso gut so tun, als wäre der Raum ein ganz gewöhnlicher flacher Raum, auf dem allerdings an unterschiedlichen Punkten ein spezielles Feld (so wie unser Temperaturfeld) die Maßstäbe aller Objekte verzerrt. Dieses Bild funktioniert nur dann, wenn alle Objekte genau gleich beeinflusst werden (wenn es in der zweidimensionalen Welt ein Objekt gibt, das sich nicht mit der Temperatur ausdehnt, dann könnt ihr mit dessen Hilfe sehen, dass sich Maßstäbe von Ort zu Ort ändern.). Genau das ist aber in der ART der Fall – letztlich ist das die Aussage des berühmten Äquivalenzprinzips, das besagt, dass alle Objekte in einem Schwerefeld gleich schnell fallen.
Die Raumkrümmung in unserem Universum ist allerdings nicht statisch, wie in unserer zweidimensionalen Modellwelt, sondern sie ist dynamisch – sie kann sich mit der Zeit ändern. Auch das können wir uns aber in unserem Modell leicht vorstellen: stellt euch beispielsweise vor, ihr würdet an einer Stelle der Platte einen Eiswürfel auflegen, dann wird die Temperatur dort niedriger – es entsteht also ein “Berg” in unserer Welt.
Auch die Ausdehnung des Universums lässt sich in unser Modell übertragen – dazu müssen wir nur die Temperatur im Laufe der Zeit immer weiter absenken – dann “schrumpfen” die Objekte in unserem Universum, also vergrößern sich die Abstände zwischen ihnen (weil ja auch die Maßstäbe mitschrumpfen). Im Modell der Kugeloberfläche dagegen lassen wir die Kugel wachsen, so wie man einen Ballon aufbläst (was ja ein beliebtes Bild für das Expandieren des Universums ist.)
Man kann den Raum also so beschreiben, als sei er gekrümmt – man kann aber genauso gut stattdessen annehmen, dass es einen zu Grunde liegenden Raum gibt (den wir allerdings nicht direkt beobachten können), der von einem “Feld” erfüllt ist (wie unserem Temperaturfeld), das alle Materie in der gleichen Weise beeinflusst (insbesondere lässt es Maßstäbe schrumpfen oder wachsen). Dieses Feld können wir dann “Gravitationsfeld” nennen.
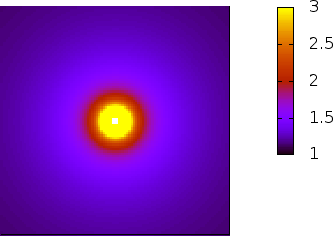
Stellt euch vor, ihr habt eine Masse, die um sich herum den Raum verzerrt. In einer zweidimensionalen Darstellung könnt ihr das genau so über die Veränderung des Maßstabs (also der Temperatur) darstellen, wie wir es oben für die Kugeloberfläche gemacht haben. So sieht das Ergebnis aus:
Die absoluten Zahlen sind dabei vollkommen willkürlich, lediglich das Verhältnis zueinander ist relevant. (Nochmal herzlichen Dank an Dieter für diesen erhellenden Kommentar.)
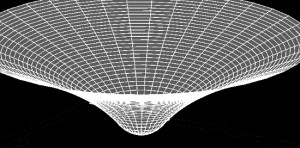
Ihr könnt euch aber auch einen gekrümmten Raum vorstellen, dort sähe das Ganze etwa so aus (wenn man den gekrümmten Raum in den dreidimensionalen Raum einbettet):
(Ausführlich habe ich dieses Bild und was es bedeutet hier erklärt). Hinweis für die Expertinnen: Die erste Darstellung verwendet isotrope Koordinaten, die zweite Schwarzschild-Koordinaten. Die Radialkoordinate ist in den beiden Bildern nicht identisch, man kann sie nicht einfach übereinander legen und direkt vergleichen. Das sieht man auch daran, dass der Weg nach Innen bei Schwarzschild-Koordinate ja immer länger wird, während in isotropen Koordinaten die Maßstäbe nach innen hin größer werden, nicht kleiner. Und noch ein Hinweis: In den Feynman Lectures sagt Feynman, dass sich die Raumkrümmung durch einen einzigen Skalenfaktor an jedem Punkt darstellen lässt. Das hat mich immer verwirrt, weil man zur Angabe der Metrik an jedem Punkt ja mehr als eine Zahl braucht, während ein Skalenfaktor nur eine Zahl ist. Das Beispiel mit den Landkarten zeigt aber, dass das täuscht, weil nicht jede Projektion für eine winkeltreue Darstellung sorgt – man muss die Abstände der Längen- und Breitengrade genau so wählen, wie Mercator das in seiner Projektion tut. Entsprechend lässt sich eine Darstellung mit einer einzigen Zahl eben nicht in jedem beliebigen Koordinatensystem realisieren, sondern nur in einem geeignet gebastelten. (Mal wieder ein Beispiel dafür, dass die Feynman Lectures zwar toll sind, dass aber vieles leider ungesagt bleibt und einen manchmal etwas hilflos zurücklässt.)
Auch wenn die beiden Bilder ganz verschieden aussehen, führen sie zu exakt denselben Ergebnissen – sie sind mathematisch zu 100% äquivalent. (Probleme könnte es allenfalls geben wenn wir an solche Dinge wie “Wurmlöcher” denken, die die Topologie unserer Welt ändern; aber da solche Objekte nicht beobachtet wurden, brauchen wir uns darüber nicht den Kopf zu zerbrechen. Selbst mit Wurmlöchern könnte man aber zumindest lokal begrenzt das Bild des simplen flachen Raums verwenden, der von einem Feld erfüllt ist.)
Ihr seht also, dass man die Raumkrümmung genau so gut über die Wirkung der Schwerkraft auf Materie beschreiben kann oder über die Krümmung des zu Grunde liegenden Raums – die beiden Bilder sind genau gleich gut.Welches Bild ihr wählt, ist letztlich Geschmackssache – wer sich vor allem mit der ART selbst beschäftigt, bevorzugt meist das Bild der Raumkrümmung, Quantenfeld- oder Stringtheoretikerinnen haben dagegen das Bild mit den Feldern lieber.
Vielleicht stellt ihr euch aber die Frage: “Und was ist mit der Zeit? Wie funktioniert das da? Ich kann mir ja noch vorstellen, dass ein Feld Objekte ortsabhängig schrumpfen oder wachsen lässt, aber wie sorgt das Feld dafür, dass Uhren schneller oder langsamer gehen?” Das ist eine knifflige Frage, für die ich leider auch keine ganz zufriedenstellende anschauliche Antwort habe, fürchte ich. Aber einiges kann ich dazu schon sagen.
Doch wieder einmal bestätigt sich der erste Hauptsatz der Bloggodynamik: Blogartikel werden immer länger, als man denkt. Deshalb vertage ich diese Frage auf einen zweiten Teil (auf den ihr aber eventuell noch ein bisschen warten müsst).









Kommentare (81)