Dass die Quantenmechanik seltsame Vorhersagen macht, die unserer (klassischen) Intuition widersprechen, ist ja nichts neues. Ein aktuelles Experiment demonstriert sehr eindrucksvoll, wie seltsam die Quantenmechanik tatsächlich ist.
Zugegeben, der eigentliche Aufbau des Experiments ist ziemlich komplex und erfordert abgefahrene moderne Quanten-Techniken wie etwa “Quantenzustandstomographie”, von denen ich auch nur ein paar Ideen verstehe. Aber zumindest das Prinzip ist eigentlich nicht so schwer zu verstehen, die Details überlassen wir dann des Expertinnen…
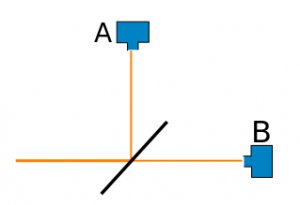
Für das Experiment verwendet man Licht, das man auf einen halbdurchlässigen Spiegel schickt. Diesen Aufbau habe ich schon vor langer Zeit mal benutzt, um die Seltsamkeiten der Quantenmechanik (QM) zu erklären:
Von links kommt ein Photon und hat am Spiegel eine 50%-Chance, nach rechts sowie eine 50%-Chance, nach oben zu fliegen. Dort sitzen Alice und Bob, zwei Physikerinnen*, die mit dem Photon herumexperimentieren können.
*Ja, wie im Moment üblich bekommt auch Bob eine grammatikalisch weibliche Form…
Jede von beiden kann natürlich nur ganze Photonen messen – wenn also Alice ein Photon misst, misst Bob keins, und umgekehrt. Das allein könnte man also auch mit den Mitteln der klassischen Physik erklären – das Photon fliegt eben entweder in die eine oder die andere Richtung. In meinem Text von damals habe ich nicht genau erklärt, wie man sicherstellen kann, dass das Photon in Wahrheit tatsächlich in einer seltsamen Überlagerung aus beiden Möglichkeiten ist und dass es sozusagen gleichzeitig bei Alice und Bob sein kann (jedenfalls solange, bis man es misst) . Genau das tut das hier vorgestellte Experiment. (Andere haben das auch schon vorher gemacht, aber dieses Experiment zeichnet sich dadurch aus, dass es die Effekte besonders klar zeigt.)
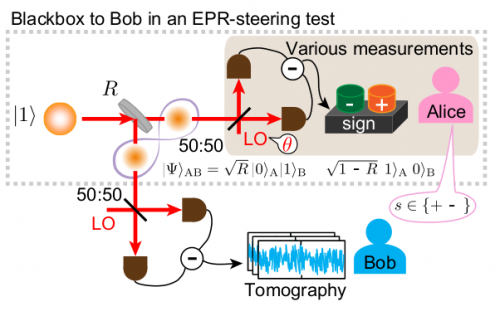
Hier ein Blick auf den Aufbau – Ihr seht, dass das Grundprinzip mit dem Spiegel dasselbe ist wie oben, aber der Rest ist “etwas” komplizierter:
Fuwa et al., s.u.
Am halbdurchlässigen Spiegel wird das Photon “geteilt” und fliegt dann zu Bob und Alice (ich denke mal, die Verbindung oder Verschränkung zwischen den beiden Möglichkeiten soll durch die graue Schleife bei “50:50” angedeutet werden.) Alice macht dann verschiedene Experimente mit dem Photon – insbesondere solche, bei denen sie die Polarisation des Photons messen kann. Bob misst ihrerseits (*s.o.) ebenfalls (mit Hilfe der “Quanten-Tomographie”) das Photon.
Das Ergebnis eines einzigen Experiments hängt in der QM ja (fast) immer vom Zufall ab. Macht man aber sehr viele Experimente, so kann man eine Statistik bekommen und kann dann etwas über den Zustand der Photonen erfahren. Bob tut genau das: Sie misst beispielsweise die Polarisation der Photonen (also die Schwingungsebene des elektrischen Feldes – ausführlich hier erklärt) und ihre Phase (genauer gesagt, die “Quadraturen” – schaut bei Wikipedia dazu, ich vertiefe das vorsichtshalber nicht, weil mir nicht zu 100% klar ist, wie genau die Messung funktioniert, der Methodenteil ist sehr knapp…).
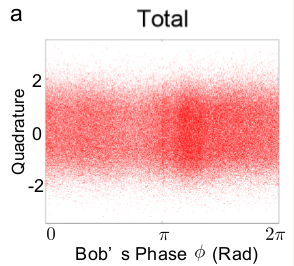
Bob hat zunächst keine Ahnung, was Alice auf ihrer Seite tut. Deswegen bekommt Bob ein statistisches Mischmasch aller möglichen Zustände, etwa so:
Fuwa et al., s.u.
Alice kann aber auf ihrer Seite Messungen machen und den Zustand des Photons auf diese Weise beeinflussen. Beispielsweise kann sie an der Phase des Photons drehen und diese beeinflussen. Diese Beeinflussung der Phase macht sich dann entsprechend auch bei Bob bemerkbar. Etwas ähnliches haben wir vor langer Zeit hier schon mal diskutiert, da war es aber ein reines Gedankenexperiment, das zwei Teilchen verwendete. Hier ist das ganze jetzt weiter verschärft, weil es ein einziges Photon ist, an dem manipuliert wird.
Nehmen wir an, dass Alice ihre Experimente macht bevor Bob irgendetwas misst. Dann ist unser Photon – nach den Regeln der Qm – also erst einmal in einem Zustand, bei dem es zum Teil in Richtung Alice und zum Teil in Richtung Bob unterwegs ist. Wenn jetzt Alice den Zustand des Photons manipuliert, dann ändert sich der Gesamtzustand des Photons, also auch der Teil, der in Richtung Bob unterwegs ist. Auf diese Weise kann Alice also den Zustand, der bei Bob ankommt, manipulieren. (Ich muss allerdings leider zugeben, dass ich an dieser Stelle die Formeln im paper nicht ganz nachvollziehen konnte – bevor Bob die Messung macht, ist der Zustand bei ihm eine Überlagerung aus einem 1-Photon-Zustand und dem Vakuum-Zustand; die Messung von Alice beeinflusst diesen Zustand. Bei der Rechnung wird dann mit Dichtematrizen hantiert – aber wie das für eine einzelne Messung funktioniert, ist mir nicht klar, vermutlich fehlt mir da irgendein Verständnistrick in Sachen Quantentomographie und “homodyne measurement”. Falls jemand das kurz erklären kann oder einen Link parat hat, hinterlasst gern einen Kommentar.)
Bob merkt davon zunächst aber nichts – denn was genau Alice getan hat, kann er nicht wissen. Er sieht ja nur das Bild von oben mit dem gleichmäigen Mischmasch.
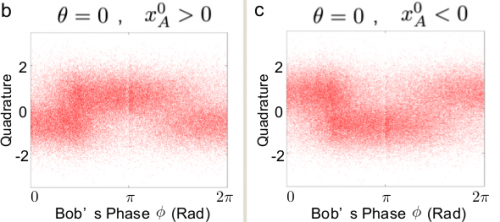
Jetzt kann Alice aber Bob sagen, wann sie den Zustand ihres “Anteils” des Photons wie beeinflusst hat, also wann sie welche Messung gemacht hat. Der Einfachheit halber beschränken wir uns auf zwei Möglichkeiten für Alices Messung, kurz mit “+” und “-” gekennzeichnet. Bob teilt jetzt seine Ergebnisse entsprechend auf, je nachdem, ob Alice ein + oder ein – gemessen hat. So sieht sein Ergebnis aus:
Die Ergebnisse von Bob und Alice sind also klar korreliert: je nachdem, was bei Alice passiert, ändern sich die Ergebnisse bei Bob. Das Photon muss also tatsächlich in irgendeiner Weise an beiden Orten zugleich sein – welche Ergebnisse die Messung bei Bob zeigt, lässt sich durch die Messung von Alice beeinflussen.
Merken kann Bob die Beeinflussung aber nur durch einen Vergleich der Ergebnisse mit Alices Messung von + oder -; ohne diesen Vergleich sieht Bob nur den Mischmasch von oben mit der gleichmäßigen Verteilung. Die Methode kann also definitiv nicht dazu verwendet werden, um Nachrichten zu schicken, weil Bob immer noch die Extra-Information über Alices Messung braucht.
Falls ihr euch übrigens die Frage stellt, wie das Experiment zur speziellen Relativitätstheorie passt (eine hinreichend schnell bewegte Beobachterin sieht ja Bobs Messung vor der von Alice) – es ist zwar im paper nicht erklärt, aber das Experiment ist in der Hinsicht letztlich symmetrisch, soweit ich sehe. Wir können genauso gut sagen, dass es Bobs Messung ist, die den Zustand des Photons festlegt und die dann die Messung von Alice beeinflusst.
Das Experiment zeigt aber noch einmal ganz klar, dass das Photon in dem Moment, wo Alice ihre Messung macht, in einem überlagerten Zustand ist. Wäre es eindeutig schon auf dem Weg zu Bob, dann könnte das, was Alice tut, ja keinen Einfluss mehr haben. Die Quantenwelt ist also wirklich ziemlich seltsam.
Fuwa, Maria, et al. “Experimental proof of nonlocal wavefunction collapse for a single particle using homodyne measurements.” Nature communications 6 (2015).






Kommentare (88)