Jetzt macht man bei A und B die Messung, unmittelbar nachdem die beiden Elektronen sich miteinander verschränkt haben, aber bevor irgendein lichtschnelles Signal hätte ausgetauscht werden können. (Da man bei A und B ja auch noch nicht wissen kann, ob die Verschränkung geklappt hat oder nicht, macht man die Messung immer – betrachtet werden aber nur die Ergebnisse, die laut der Messung bei C auch verschränkt sind.)
Hier ein Schema, das den Zeitablauf verdeutlicht:
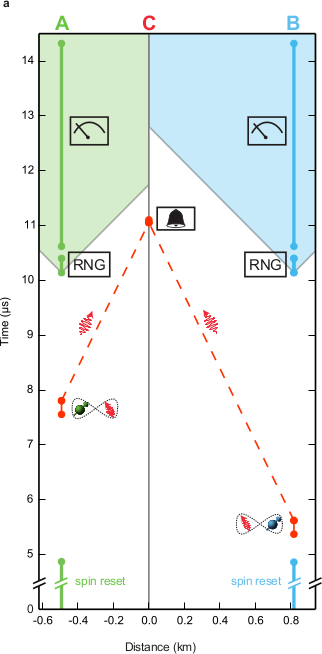
Aus Hensen et al., s.u.
Am Anfang werden bei A und B die Spins der Elektronen initialisiert. Die beiden Elektronen senden – passend zeitversetzt, damit das Signal bei C gleichzeitig ankommt, jeweils ein Photon aus. Bei C werden die beiden Photonen zusammengeführt und geschaut, ob eine erfolgreiche Verschränkung vorlag (dafür steht die Alarmglocke). Parallel dazu (und zwar so, dass kein Lichtsignal ausgetauscht werden kann) wird bei A und B der Spin gemessen. (Die schrägen Linien mit der Schattierung zeigen an, wie ein Signal mit Lichtgeschwindigkeit von A nach B käme oder umgekehrt.)
Wie ihr seht, ist alles zeitlich so gelegt, dass sich die Messungen bei A und B nicht gegenseitig beeinflussen können. Das Lokalitäts-Schlupfloch ist also geschlossen.
Und weil bei der Auswertung das Ergebnis von C (die Alarmglocke) verwendet wird und nur diejenigen Ergebnisse bei A und B in die Auswertung einbezogen werden, wo die Verschränkung erfolgreich war, ist auch das zweite Schlupfloch dicht. Nicht-detektierte oder verworfene Verschränkungen oder ähnliche Effekte können keine Rolle spielen, weil nur diejenigen Fälle angeguckt wurden, wo die Verschränkung erfolgreich war.
Allerdings führt das auch dazu, dass nur eine kleine Zahl von Messungen gemacht werden konnte. Eine erfolgreiche Verschränkung gab es nur etwa einmal pro Stunde der Experiment-Laufzeit. Insgesamt wurden 245 Messungen an verschränkten Elektronen gemacht und ausgewertet.
Das Ergebnis ist aber eindeutig: die Bellsche Ungleichung wurde verletzt. Da die Bellsche Ungleichung aber ja etwas über Wahrscheinlichkeiten aussagt, kann es natürlich immer noch sein, dass man einfach Glück (oder Pech) hatte, und dass die Verletzung der bellschen Ungleichung durch Zufall zu stande kam. Die Wahrscheinlichkeit dafür (der p-Wert) ist aber klein – sie liegt bei knapp 2% (bzw. 4%, wenn man ein etwas andere statistische Auswertung macht – ich habe den Unterschied nicht exakt verstanden, wird aber auch im verlinkten physicsforum-Artikel diskutiert, falls jemand mehr wissen will). Weitere Experimente werden den Wert sicherlich noch drücken.
Vollkommen ausgeschlossen ist es also nicht, dass die Welt sich doch nach den Regeln der klassischen Physik verhält – aber die Natur müsste schon ziemlich tricksen, damit bei den früheren Experimenten, die jeweils ein Schlupfloch schließen, die Bellsche Ungleichung sehr deutlich (und mit viel höherer statistischer Sicherheit) verletzt wurde und jetzt hier, wo man beide Schlupflöcher schließt, etwas ziemlich Unwahrscheinliches passiert.
Alles in allem scheint die Natur tatsächlich nicht-lokal oder nicht-realistisch zu sein (oder sogar beides). Und auch wenn die meisten Physikerinnen das angesichts der experimentellen Evidenz auch vorher nicht angezweifelt haben, ist es gut, jetzt ein Experiment zu haben, dass die Schlupflöcher, die es noch gab, schließt.
Hensen, B., et al. “Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres.” Nature 526.7575 (2015): 682-686. arXiv:1508.05949






Kommentare (116)