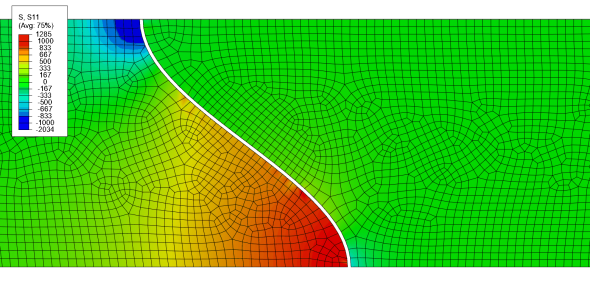
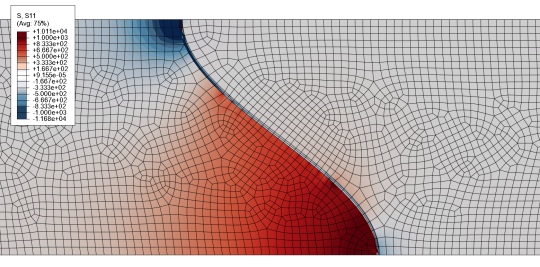
Nein, keine Sorge, das hier ist kein Aufruf dazu, den Himmel anzumalen oder die Sonne loszuwerden, damit es in Zukunft keine Regenbögen mehr gibt. Hier geht es um Regenbögen, wie man sie des öfteren in wissenschaftlichen Veröffentlichungen findet. Beispielsweise in Bildern wie dem hier oben.
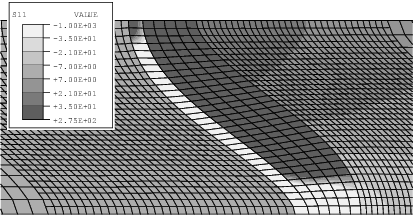
Das Bild zeigt den Spannungsverlauf in einem Schichtsystem (einer Wärmedämmschicht), aber die Details spielen hier gar keine Rolle. Mir geht es nur um das Farbschema. Das verwendete Schema ist in unserem Simulationsprogramm (ABAQUS genannt) die Standard-Einstellung, auch andere Programme verwenden ähnliche Schemata (Matlab zum Beispiel, soweit ich weiß). Die Farbverläufe sollen es leichter machen, zu erkennen, wie sich die Spannungen verhalten – hier mal ein ähnliches Bild aus der Druckversion einer Veröffentlichung, also in schlichtem Schwarz-Weiß:
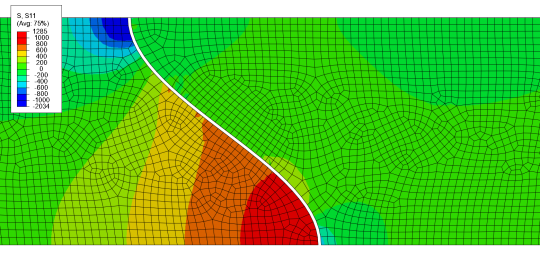
Keine Frage, dass die Farbversion deutlich schöner ist, oder? Wobei ich in der Farbversion einen kontinuierlichen Verlauf genommen habe, keinen mit scharfen Abstufungen, der sähe so aus:
Allerdings hat die Farbversion auch einen deutlichen Nachteil. Wenn ihr mal oben auf die Skala schaut, dann seht ihr, dass wir im blauen und grünen Teil einen ziemlich großen Bereich von Werten abdecken, bei denen die Farben sich nur wenig unterscheiden, während wir im gelben Bereich des Spektrums vergleichsweise schnell wechselnde Farben haben.
Das hängt damit zusammen, dass unsere Augen im rot-grünen Bereich des Spektrums besonders empfindlich auf Farbunterschiede reagieren, während wir im blauen Bereich auch deutlich unterschiedliche Lichtwellenlängen mit sehr ähnlicher Farbe wahrnehmen. (Warum das so ist und was Dinosaurier damit zu tun haben, erkläre ich hier.) Entsprechend sehen wir Unterschiede im rot-gelben Bereich deutlich stärker als im blau-grünen. (Jedenfalls, solange ihr nicht farbfehlsichtig seid, ansonsten ist das Regenbogenspektrum für euch eh nicht so toll…)
Wie drastisch dieser Effekt sein kann, zeigt zum Beispiel diese Abbildung [Borland und Taylor]:
Ihr seht zwei Datensätze, einen in der linken und einen in der rechten Spalte. Wie man am mittleren Bild mit den Graustufen gut sehen kann, ist der Verlauf links eigentlich sehr glatt – aber das Farbspektrum mit dem Regenbogen suggeriert, dass zum Beispiel in der Mitte im grünen Bereich wenig passiert, bis dann ein scharfer Übergang zu Gelb stattfindet. Umgekehrt sieht man die doch einigermaßen deutlichen Sprünge in den rechts dargestellten Daten im Regenbogenplot eigentlich nicht.
So ein Regenbogenspektrum kann also massiv in die Irre führen. (Ein anderes schönes Beispiel findet ihr hier. Der Artikel von Silva et al. gibt einen ganz guten Überblick über verschiedene Aspekte.)
Tatsächlich habe ich schon bei einer meiner letzten Veröffentlichungen ein anderes Farbschema verwendet, das zwar Unterschiede nicht alle ganz gleich gewichtet, aber trotzdem deutlich weniger irreführend ist:
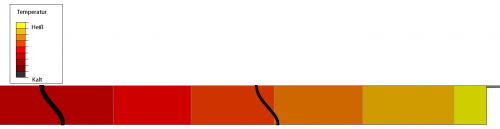
Allerdings ist auch dieses Farbspektrum für dieses Problem nicht ideal. Worüber ich nämlich – bis vor kurzem – nie nachgedacht habe, ist, dass Farbspektren je nach Art der Daten unterschiedlich sein sollten. Wenn ihr einen einfachen Werteverlauf habt (z.B. von kalt nach heiß), dann ist ein verlauf mit zwei Randfarben, die fließend ineinander übergehen gut geeignet. Hier ein Temperaturverlauf in einer Schicht:
Ein solcher Farbverlauf heißt sequentiell. (Alternativ kann man – gerade für Temperaturen – ein Farbschema nehmen , bei dem der Verlauf von Schwarz nach Weiß analog zum Schwarzkörperspektrum geht, wie in der unteren Zeile bei den Bildern aus dem paper oben – mein schwarz-rot-gelb-Spektrum oben geht ein bisschen in diese Richtung.)
Bei dem Bild darüber allerdings trage ich Spannungen auf (das S22 in der Legende steht für eine Spannungskomponente). Da ist es so, dass Stellen, wo die Spannungen um Null liegen, nicht so interessant sind wie die, wo die Spannung stark von Null abweicht – egal ob in positiver oder negativer Richtung. beide Extreme sollten hervorgehoben werden. Dafür braucht man ein anderes Farbschema – ein divergentes.
In einem divergenten Schema hat man zwei deutlich unterschiedliche Farben an den Ende und eine neutral aussehende Farbe in der Mitte. Also beispielsweise blau-weiß-rot. So sieht die Spannungsverteilung aus dem Bild oben in diesem Schema aus:
Man erkennt gleich, wo die uninteressanten Bereiche sind und wo spannungsmäßig der Bär steppt. Irreführende Farbsprünge gibt es auch keine. Zugegeben, das ganze ist nicht so bunt und auf den ersten Blick auch sehr ungewohnt – dafür ist das Schema aber genauer.
Falls ihr jetzt denkt, dass das ganze doch eine ziemlich müßige Spielerei ist – weit gefehlt. O.k., wenn ich bei unseren Spannungsverteilungen nicht gleich sehe, was Sache ist, ist das nicht so schlimm, zum Auswerten verlasse ich mich eh nicht auf die bunten Bildchen sondern lese Zahlenwerte an kritischen Punkten aus. Aber auch zum Beispiel in der Medizin verlässt man sich ja oft auf Visualisierungen. Ein schönes Beispiel liefert ein paper von Borkin et al. Da geht es um die Spannung Spannung in Arterien – wenn die zu klein ist, ist das ein Hinweis auf eine gefährliche Erkrankung. (Fragt mich nicht, wie das genau gemessen wird…) Um zu sehen, wie Menschen auf unterschiedliche Farbschemata reagieren, wurden ihnen dieselben Daten in unterschiedlichen Darstellungen gezeigt (aus Borkin et al. ):
Nahezu alle Testpersonen waren sich einig, dass die Regenbogendarstellung am schönsten ist – obwohl sie dafür plädierten, das Farbschema umzudrehen, weil die kritischen Bereiche mit niedrigen Werten rot sein sollten, nicht blau. Sehr gut auszulesen ist auch das reine Graustufenbild, das allerdings nicht gut ankam, weil Medizinerinnen mit reinen Graubilder Rohdaten verbinden, die noch nicht ausgewertet wurden. Sollte man also doch bei den Regenbögen bleiben?
Um das herauszufinden, bekamen die Versuchspersonen anschließend die Aufgabe, die kritischen Regionen selbst per Maus anzuklicken, und durften dann bewerten, wie einfach oder schwierig sie das fanden. Und dabei zeigte sich, dass ein divergierendes Farbschema (Schwarz/rot, wie oben in Teilbild F) zu signifikant weniger Fehlern führte als das Regenbogenschema. Verwendet man zweidimensionale Bilder, so wie oben, dann werden beim divergierenden Farbschema 91% der kritischen Stellen erkannt, beim Regenbogenspektrum nur 62%. Interessanterweise verwendeten die Versuchspersonen dabei weniger Zeit, wenn die Bilder das Regenbogenspektrum verwendeten. (Man kann natürlich spekulieren, ob das daran liegt, dass das Regenbogenspektrum deutlich vertrauter ist oder ob es eine falsche Sicherheit vermittelt.) Es zeigt sich also, dass die Verwendung des richtigen Farbspektrums durchaus wichtig sein kann.
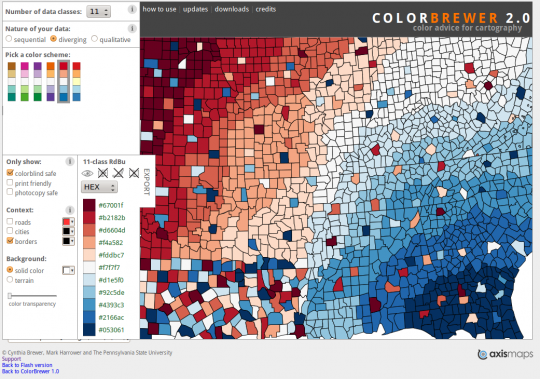
Wenn ihr selbst passende Farbspektren für eure Grafiken braucht, dann habe ich hier die perfekte Internetseite: ColorBrewer. (Erstellt von Cynthia Brewer, die auch viel zum Thema veröffentlicht hat, ein Beispiel findet ihr unten in der Literaturliste.) Dort könnt ihr Spektren nach eurem Geschmack auswählen und euch auch die Farbwerte ausgeben lassen (das habe ich auch für das blau-rot-Schema oben gemacht) – das Ganze hat sogar einen Knopf, der erlaubt, nur solche Spektren zu wählen, die auch für farbfehlsichtige Menschen noch erkennbar sind:
Screenshot von ColorBrewer.
Die Farbspektren sind so ausgeklügelt, dass sie auch zum Einfärben von Karten dienen können, wo auch mal zwei Gebiete aneinandergrenzen können, die ganz unterschiedliche Werte haben. (Was bei meinen Plots selten vorkommt.) Sie sind extra so gemacht, dass man trotzdem alles gut unterscheiden kann – im Bild z.B. links und rechts unten zu sehen. Trotz dieser harten Anforderungen gibt es aber einige Spektren zum Auswählen in verschiedenen Farbklängen. Ihr könnt euch also nach Herzenslust bedienen.
Der Regenbogen ist bei den Spektren übrigens nicht dabei. Der gehört nämlich an den Himmel, nicht in eure Veröffentlichung.









Kommentare (38)