E=mc² ist ja die Gleichung der Physik schlechthin, und auf jeden Fall die Gleichung der speziellen Relativitätstheorie. Man sollte also meinen, dass sie direkt aus den Annahmen der SRT folgt und dass sie natürlich in Einsteins Arbeit “Über die Elektrodynamik bewegter Körper” eine zentrale Rolle spielt. Dem ist aber nicht so – der Artikel, in dem die SRT eingeführt wurde, enthält die Gleichung E=mc² in keiner Form. Einstein hat sie kurz nach Veröffentlichung der SRT in einem anderen Artikel zum ersten Mal aufgestellt.
Wie der Beweis nicht geht
Zugegebenermaßen liegt die Annahme, dass E=mc² direkt ohne weiteres aus der SRT folgt, auch deswegen nahe, weil viele Bücher genau das schreiben. Häufig (beispielsweise in Schulbüchern, ich zitiere gleich ein Beispiel) wird die Gleichung E=mc² in etwa so “hergeleitet”:
Aus den Gleichungen der SRT kann man die Bewegungsenergie (kinetische Energie) einer Masse berechnen. (Wie man das prinzipiell macht, erkläre ich nachher noch kurz.) Die ist gegeben durch
Dabei ist das γ ein Faktor, der so von der Geschwindigkeit abhängt und den ich im zweiten teil des Artikels schon eingeführt habe:
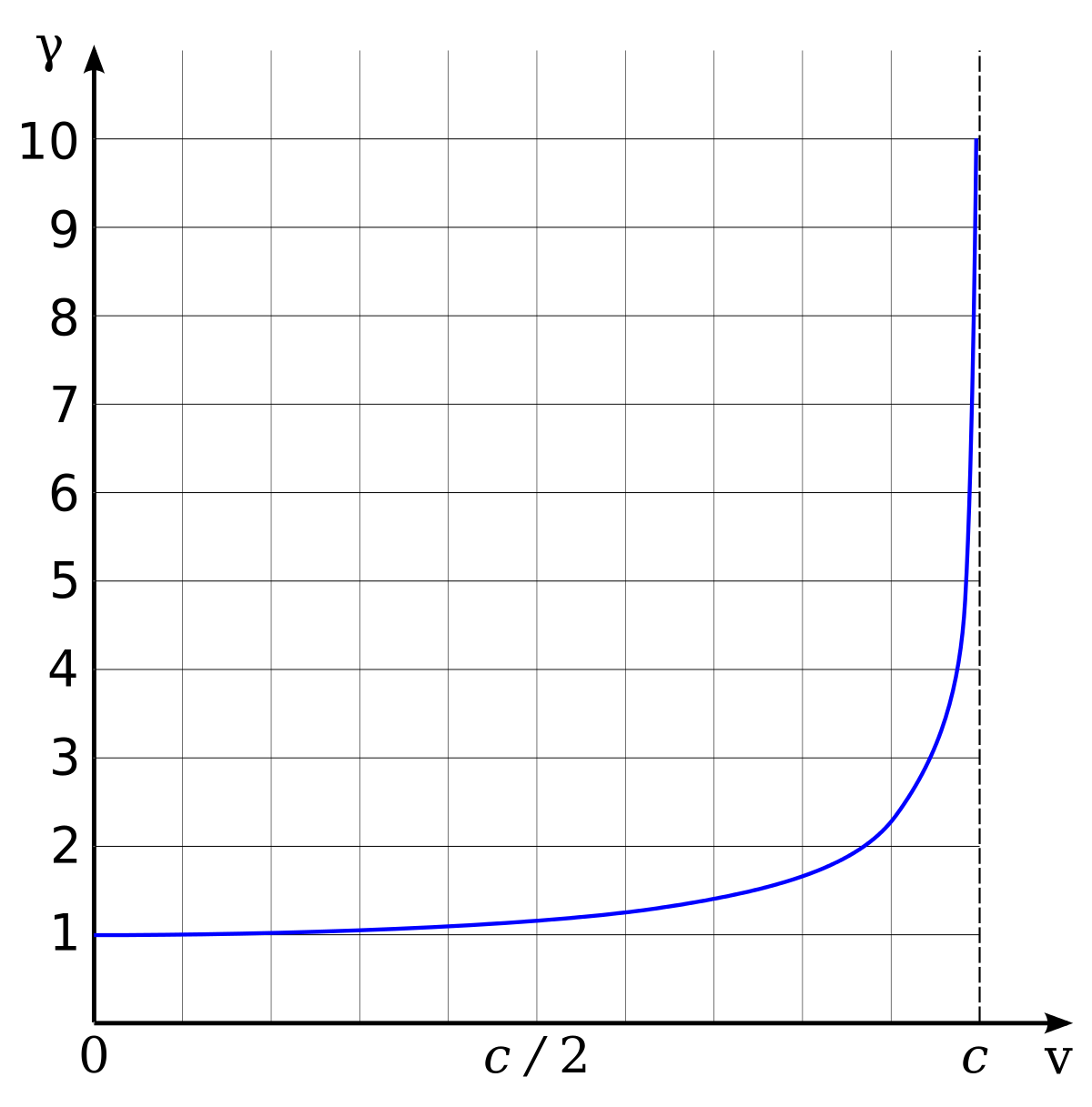
Von egg, Graph created with KmPlot, edited with Inkscape Trassiorf (talk) 21:54, 2 March 2010 (UTC) – Eigenes Werk, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=2868331
Hier und im Folgenden ist m immer die Ruhemasse, nicht die relativistische Masse, für die verwende ich immer explizit den Faktor γ. (Den Unterschied zwischen beiden habe ich auch im zweiten Teil des Artikels erklärt – ist zugegebenermaßen schon ein bisschen her, aber ich musste zwischendurch mal Urlaub machen…)
Für Geschwindigkeit Null ist der Faktor (γ-1) natürlich Null, die Bewegungsenergie verschwindet. Jetzt kann man die Klammer mit dem γ ausmultiplizieren, dann bekommt man die Gleichung (die ich jetzt explizit mit der relativistischen Masse schreibe)
.
Im Physikbuch Dorn/Bader 12/13 wird jetzt ganz “elegant” so argumentiert: (mit etwas anderen Formelzeichen, ich setze hier meine Symbole ein)
Die Terme mrel c², mc² und Ekin sind Energie. Ein ruhender Körper hat Ekin=0, er hat nur die Ruheenergie mc². Also ist Ekin= (mrel-m)c² tatsächlich die relativistische Form der kinetischen Energie. Bei Bewegung erhöht sie E=mc² auf die Gesamtenergie E=mrel c². Diese Gleichung hat als “E=mc²” Weltgeschichte gemacht. Sie zeigt: Energie und Masse sind äquivalent.
Sieht ganz gut aus, oder? Ist aber keine Herleitung, nicht mal ansatzweise. Warum nicht? Weil wir schlicht reinstecken, was am Ende rauskommen soll: Wir haben aus der SRT nur die Gleichung für die kinetische Energie hergeleitet. Diese enthält einen Term mc² (mit m als Ruhemasse), den wir von mrel c² abziehen. Dass der Term mc² für die Ruhemasse selbst irgendeine physikalische Bedeutung hat, ist dadurch in keiner Weise gezeigt – der Begriff “Ruheenergie” wird hier einfach eingeführt.
Tatäschlich ist es ja in der Physik normalerweise so, dass man den Nullpunkt der Energie frei wählen kann. (Es gibt Ausnahmen, spätestens in der ART, aber in der klassischen Physik geht es eigentlich immer.) Dass in unserer Gleichung für die kinetische Energie also ein Term vorkommt, den wir abziehen, sagt nichts darüber, dass dieser Term eine physikalische Bedeutung hat, und schon gar nichts darüber, dass diese Bedeutung die einer “Ruheenergie” ist.
Also: Klar ist mc² eine Energie – die Frage ist aber eben die, welche Bedeutung sie hat. Wir können sie natürlich auch “Ruheenergie” nennen, aber sinnvoll ist das nur dann, wenn wir zeigen können, dass man diese Energie – wie andere Energien auch – umwandeln kann. (Im ersten Teil des Artikels haben wir ja gesehen, was die Äquivalent von Energie und Ruhemasse bedeutet, beispielsweise für eine Tafel Schokolade.)
Wer sich mit der mathematischen Seite der SRT auskennt, mag vielleicht so argumentieren: In der SRT ist es ja so, dass Raum und Zeit miteinander vermischt sind. Wenn zwei Beobachterinnen sich mit unterschiedlicher Geschwindigkeit bewegen, dann sind sie sich über räumliche Abstände zwischen zwei Punkten oder zeitliche Abstände zwischen zwei Ereignissen nicht einig, sondern bekommen unterschiedliche Werte heraus. Mathematisch kann man das so lösen, dass man Raum und Zeit zu einem Gesamtobjekt zusammenfasst. Jede Größe, die in der klassischen Physik einen Punkt oder eine Richtung im Raum beschreibt (beispielsweise die Geschwindigkeit, die ja einen Wert und eine Richtung hat – beispielsweise 20km/h nach Südsüdost), bekommt jetzt eine weitere, zeitliche Komponente. Solche Größen nennt man Vierervektoren (habe ich mal hier etwas ausführlicher erklärt).
Macht man diese Rechnung für den Impuls (also, in der klassischen Physik, Masse mal Geschwindigkeit), so stellt man fest, dass die vierte Komponente einen Term für die kinetische Energie enthält. Zusätzlich hat sie aber noch einen zweiten Term, der gerade gleich mc² ist. Dieser Term ist also auch eine Energie, da er auch für ein ruhendes Teilchen da ist, ist er die Ruheenergie.
Ja, nett – aber leidet letztlich an demselben Problem: Wir haben einen Term E=mc², der die Form einer Energie hat – aber die Frage ist natürlich, was das für eine Energie ist und ob diese Energie irgendwelche physikalischen Konsequenzen hat. Und das lässt sich mit dieser “Herleitung” eben genau nicht zeigen.
So geht es also nicht. Wie dann?






Kommentare (84)