Im letzten Artikel habe ich euch ja gezeigt, wie man aus der Berechnung von Energie Rückschlüsse darauf ziehen kann, wie sich eine Legierung verhält und welche Phasen darin günstig sind. Dazu habe ich die Energie von Elektronen in einem Kristall berechnet, beispielsweise in Nickel oder der delta-Phase. Die Position der Atome war dabei allerdings vorgegeben – jedenfalls habe ich so getan, als ob das so wäre.
In Wahrheit stimmt das aber so nicht. Nehmen wir erst mal reines Nickel. Der Abstand der Atome (die “Gitterkonstante”) wird dadurch bestimmt, dass die Atome die energetisch günstigste Position einnehmen. Würde man sie enger zusammenrücken, dann würde die Abstoßung der Atomkerne und die Tatsache, dass Elektronen sich nicht so gern auf engen Raum zusammenquetschen lassen, dazu führen, dass sich die Energie erhöht, würde man sie weiter auseinanderziehen, würde die Bindung zwischen den Atomen insgesamt schwächer werden. Es gibt also einen optimalen Abstand, und der bildet sich in der Natur heraus.
In unserer Simulation gibt es entsprechend auch einen optimalen Abstand – der muss aber nicht exakt derselbe sein. Das liegt daran, dass unser Verfahren ja ein paar Näherungen enthält (insbesondere eine Näherung für die Wechselwirkung der Elektronen). Natürlich sollte die Gitterkonstante in der Simulation schon zum realen Wert passen, aber exakt identisch wird sie nicht sein. Wenn wir die minimale Energie in unserem simulierten System bestimmen wollen, sollten wir also die Gitterkonstante berechnen, bei der die Energie tatsächlich am kleinsten ist.
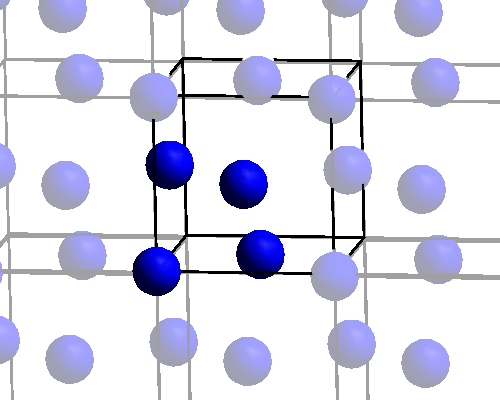
Das können wir dadurch tun, dass wir einfach mehrere Werte für die Gitterkonstante ausprobieren. Wir basteln uns eine kleine Zelle aus 4 Nickel-Atomen, die repräsentativ für den Kristall ist (wir nutzen also periodische Randbedingungen, wie im ersten Teil erklärt):
Diese Zelle hat eine bestimmte Kantenlänge – wir können die als “Gitterkonstante” nehmen, weil wir das Gitter durch Aneinanderreihen von lauter solchen Würfeln aufbauen können. (Beim Begriff “Gitterkonstante” muss man etwas aufpassen, je nach Zusammenhang nimmt man den Abstand nächster Nachbarn im Gitter oder wie ich ab jetzt die Kantenlänge einer Zelle, aus der sich das Gitter besonders bequem aufbauen lässt, hier also die Länge einer Würfelkante.)
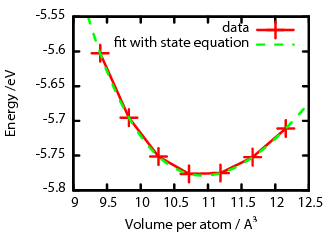
Wir machen jetzt einfach eine Handvoll Simulationen mit leicht unterschiedlicher Gitterkonstanten und berechnen jeweils die Energie. Dann plotten wir das Ganze. Heraus kommt das:
Hier habe ich nicht die Gitterkonstante auf der x-Achse aufgetragen, sondern das Volumen pro Atom, aber die beiden Größen hängen natürlich zusammen – je größer ich den Würfel mache, desto länger wird die Kante und desto mehr Volumen entfallen auf ein Atom. Die roten Datenpunkte zeigen die berechneten Werte. Man kann jetzt eine Kurve durch diese Werte legen (ich nutze dazu die Birch-Murnaghan-Gleichun) und deren Minimum gibt dann die optimale Gitterkonstante an. Für Nickel bekomme ich in der Rechnung hier eine Gitterkonstante von 0,3523 Nanometer, was sehr dicht am gemessenen Wert liegt. Man kann auf die Weise auch gleich noch herausbekommen, wie leicht sich das Material komprimieren lässt (den sogenannten Kompressionsmodul), das Ergebnis fällt bei meinen Rechnungen ein paar Prozent größer aus als der experimentell gemessene Wert, aber perfekte Übereinstimmung kann man wegen der Näherungen auch nicht erwarten..
Expertinnenhinweis: Die Software VASP, die ich verwende, erlaubt die Anpassung der Gitterkonstanten in einer einzigen Rechnung. Diese Option (Parameter ISIF) spart zwar ne Menge Rechenzeit, aber sie ist weniger genau: Die berechnete Gitterkonstante weicht von der mit der Minimums-Methode bestimmten ab und die Energie der Endkonfiguration ist signifikant höher. (Ich habe bei Zellen mit 32 Atomen Abweichungen von bis zu knapp 40meV gefunden, das ist schon ziemlich viel…). Generell empfiehlt auch das Handbuch, das Volumen der Zelle bei Rechnungen mit hoher Genauigkeit konstant zu lassen; die Zellform kann man anpassen, das ist o.k.
Wir können jetzt also die Gitterkonstante berechnen. Wenn wir ein Legierungsatom in unsere Zelle stecken (dazu nimmt man dann eine Zelle mit z.B. 32 Atomen), dann wird die Sache allerdings komplizierter: Nicht alle Atome haben dieselbe Elektronenaffinität oder denselben Atomradius. (Generell ist der Atomradius eine ziemlich unscharf definierte Angelegenheit, weil wir ja Elektronenwolken haben, die die Atomkerne umgeben und die keinen genau definierten Durchmesser haben. Packt man die Atome in einen Kristall, ändert sich die Elektronenwolke – deswegen machen wir ja diese Rechnungen – und entsprechend ändert sich auch der Atomradius.) Stopft man ein Atom in Nickel, dann wird es die Nickelatome um sich herum entweder wegdrängen oder an sich heranziehen, beispielsweise so:
Stopft man ein “großes” Atom in den Kristall, übt es eine Kraft auf die anderen Atome aus, um sie wegzuschieben, ein “kleines” Atom zieht die anderen zu sich heran. Diese Kraft lässt sich berechnen, wenn wir den Zustand der Elektronen kennen. Das geht dank des sogenannten Feynman-Hellmann-Theorems.
Wir gehen also folgendermaßen vor: Wir ersetzen ein Ni-Atom durch ein anderes (wie Mangan, Eisen oder so). Dann berechnen wir wie bisher die Energie. Daraus können wir dann den Zustand der Elektronen (die Wellenfunktion unseres “Hilfsproblems” aus Teil 1) berechnen. Damit bekommen wir mit dem Feynman-Hellmann-Theorem die Kraft, die auf jedes Atom (also auf dessen Atomkern) wirkt.
Wir verschieben dann die Atomkerne in Richtung der wirkenden Kraft ein kleines Stück und rechnen wieder von vorne los. Das tun wir solange, bis die Kraft auf die Atomkerne hinreichend klein ist, denn im Kräftegleichgewicht (also der energetisch günstigsten Position der Atome) ist die Kraft auf ein Teilchen ja Null. (Stellt euch als Beispiel eine Kugel vor, die zwischen zwei Federn eingespannt ist. Wenn die Kugel ruht, ist die Kraft der beiden Federn genau entgegengesetzt und gleich groß.) Auf diese Weise können wir also die Anordnung der Atome auch anpassen – das Ganze kostet aber natürlich entsprechend mehr Rechenzeit, weil wir die Elektronen ja nicht nur einmal, sondern mehrfach berechnen müssen, denn wenn wir die Atome verschieben, ändern sich natürlich auch die Wellenfunktionen.
Zusätzlich kann das Legierungsatom natürlich die Gitterkonstante als Ganzes beeinflussen, weil das Atom ja vielleicht besonders groß oder besonders klein ist; die Zelle wird also etwas schrumpfen oder größer werden. Wir sollten also die Prozedur von oben verwenden und die Simulation mit unterschiedlichen Gitterkonstanten machen, um das Optimmum zu finden.
Tatsächlich habe ich dieses Verfahren genau so bei den Ergebnissen angewandt, die ich im letzten Teil erklärt habe. Ich habe für jedes Legierungselement in Nickel und in der delta- und eta-Phase unterschiedliche Gitterkonstanten verwendet und ich habe für jede Gitterkonstante den Atomkernen erlaubt, sich zu bewegen. Das erklärt auch, warum das Ganze doch ne Menge Rechenzeit (ein paar zehntausend Prozessorstunden) geschluckt hat.
Mit dieser Technik kann man also die Atome in ihren Positionen so “hinruckeln”, dass sie energetisch möglichst günstig angeordnet sind. Man könnte jetzt auf die Idee kommen, dass man damit jede beliebige Kristallstruktur berechnen kann: Statt die Nickelatom in der richtigen Anordnung in meinem Simulationsvolumen zu platzieren, könnte ich sie natürlich auch einfach irgendwie reinstopfen und sehen, in welche Positionen sie sich schließlich begeben. Ganz so einfach ist das jedoch nicht – wir haben es hier mit einem komplizierten Minimierungsproblem zu tun (bei welcher Anordnung der Atome ist die Energie minimal?), und solche Probleme sind notorisch schwer zu lösen. Wenn ich die Nickelatome am Anfang in beliebige Positionen bringe, dann werden sie sich zwar etwas günstiger anordnen, aber ob diese Anordnung tatsächlich die absolut beste ist, ist nicht klar. (In Fachsprache: Wir finden ein lokales, aber nicht unbedingt ein globales Optimum.)
Wenn man die optimale Kristallstruktur nicht kennt, geht man deshalb meist anders vor: Man probiert plausible Kristallstrukturen aus und vergleicht deren Energie. Die Struktur mit der niedrigsten Energie ist dann die richtige. (Man kann auch komplexere Optimierungsalgorithmen verwenden und zum Beispiel Atome herumtauschen und ähnliches, da gibt es inzwischen eine Menge Werkzeuge, mit denen ich aber wenig Erfahrung habe.) Wenn man hinreichend viel Computerpower hat, dann kann man eine ganze Menge Kombinationen durchspielen. Ich nutze zum Beispiel gern die “open quantum molecular database”, die hat einige 100000 Einträge. Tippt ihr da bei der Suchmaske zum Beispiel Ni3Nb ein, dann bekommt ihr Daten zur Delta-Phase.
Nachdem ihr jetzt einen kleinen Überblick über die Methode bekommen habt, schauen wir zum Abschluss noch ein paar Anwendungen an.
Eine interessante Anwendung der DFT-Methode findet sich in der Astronomie: Lange Zeit hat man sich ja gefragt, wie genau der Jupiter aufgebaut ist (und ganz klar ist das anscheinend imme rnoch nicht). Der besteht ja vor allem aus Wasserstoff und Helium. Im Inneren des Jupiter steht dieses Material unter extrem hohen Druck; theoretisch ist es dabei möglich, dass der Wasserstoff sich dann wie ein Metall verhält. Genau so etwas lässt sich natürlich prima mit der DFT-Methode untersuchen: Wir setzen unseren Würfel unter extremen Druck (dazu nehmen wir eine eigentlich zu kleine Gitterkonstante) und schauen, welche der denkbaren Strukturen dann energetisch am günstigsten ist. Dazu gibt es eine Menge Veröffentlichungen, so dass ich keinen perfekten Überblick über alles habe (vornehme Umschreibung für “ich habe eigentlich keinen blassen Schimmer…”), aber soweit ich es verstehe, lässt sich auf diese Weise zeigen, dass man im Jupiter tatsächlich metallischen Wasserstoff erwarten sollte. So stellt man sich den Jupiter vor: ganz innen ist ein Kern aus Fels und Eis, drum herum ist aber eine dicke Schicht aus metallischem Wasserstoff:

By Kelvinsong – Own work, CC BY-SA 3.0, Link
Und auch das ist noch nicht alles. Wir haben bisher ja immer nur Grundzustände angeguckt. Bei höheren Temperaturen ändern sich kristallstrukturen allerdings. Die Elektronen tun bei moderaten Temperaturen bis 1000 oder 2000 Grad nicht besonders viel, die sind immer noch im wesentlichen im Grundzustand. (Die Temperatur, bei der die Elektronen signifikant beeinflusst werden, ist die Fermi-Temperatur, die liegt typischerweise bei 10000 Grad.) Die Atome selbst aber fangen an zu schwingen, wenn es warm wird. Den Einfluss solcher Gitterschwingungen kann man mit der Methode ebenfalls berechnen. Das ist ziemlich aufwändig, weil man dazu gucken muss, welche Kräfte auf die Atome wirken, wenn man sie aus ihrer Ruhelage auslenkt, und wenn man mehrere unterschiedliche Atome in seiner Zelle hat, dann gibt es dazu ne Menge Möglichkeiten, die berechnet werden müssen. (Deswegen habe ich auch gerade seeehr viel Rechenzeit im HLRN bekommen…) Wenn man diese Schwingungen berücksichtigt, dann kann man aber zum Beispiel ausrechnen, wie sich das Material thermisch ausdehnt. Das ist bei unseren Nickel-Legierungen wichtig, weil zum Beispiel ein sehr kleines delta-Teilchen, das in Nickel eingebettet ist, eine höhere Energie hat, weil die Gitterkonstanten nicht zusammenpassen. Entsprechend muss man die Gitterkonstanten vergleichen, und zwar nicht bei Temperatur Null (da können wir das Zeug schlecht schmieden), sondern bei der Temperatur, wo das Material tatsächlich bearbeitet wird.
Ganz andere und sehr vielfältige Anwendungen hat die Methode schließlich in der Chemie – dort kann man dann tatsächlich schauen, wie chemische Reaktionen stattfinden, ob eine Oberfläche als Katalysator für eine Reaktion taugt und alles, was Chemikerinnen noch so tun (wovon ich aber wenig Ahnung habe…). Auch in der Medizin ist das beispielsweise wichtig, ein Beispiel findet ihr hier.
Ihr seht also, dass man mit der DFT-Methode eine ganze Menge machen kann. Diese Serie hat euch hoffentlich zumindest einen kleinen Einblick in die Möglichkeiten gegeben.







Kommentare (4)