In der Raumzeit
Teresa Mite, eine entfernte Verwandte von Anna, lebte weit weit fort, in einem seltsamen Land, der “Region für andere und merkwürdigere Zeitgenossen, inklusive Termiten”, kurz “RAUMZEIT”. In der Raumzeit war vieles anders als in Annas Raum. Auch hier gab es zwei Richtungen, aber die beiden verhielten sich unterschiedlich. Abstände in der einen Richtung konnte Teresa (genau wie Anna) beispielsweise mit einem Maßband messen. Weil sie in dieser Richtung dieselben Maßstäbe wie Anna benutzen konnte, nannte sie diese Richtung nach Annas Heimat “Raum”. In der anderen Richtung aber brauchte Teresa ein ganz anderes Messgerät, genannt “Uhr”. Abstände in dieser Richtung hatten für Teresa erst einmal nichts damit zu tun, wie sich Abstände im Raum verhielten, sie waren etwas ganz anderes. Diese Richtung nannte Teresa (wegen des Namens ihrer Heimat, die ja “Raumzeit” hieß”, “Zeit”.
Teresa konnte also auch ein Gitter zeichnen, mit Linien, die den Abstand im Raum oder den Abstand in der Zeit angaben. Zwei Punkte, die auf derselben Zeitlinie lagen, hatten einen Abstand im Raum, den Teresa an den Gitterlinien abzählen konnte, genau wie Anna den Abstand zu ihrer Freunding Berta. Zwei Punkt, die auf derselben Raumlinie lagen, hatten einen Abstand, den Teresa auch durch Abzählen von Gitterlinien bestimmen konnte, dieser Abstand war jetzt aber natürlich ein Zeitabstand.
Weil sie räumliche und zeitliche Abstände nicht mit dem gleichen Maßstab messen konnte, konnte sie aber den Abstand zwischen zwei Punkten, die irgendwie zueinander lagen (so wie Clara von Anna aus gesehen), nicht als eine Zahl angeben, sie musste sagen “Vier Gittereinheiten im Raum, drei Gittereinheiten in der Zeit”.
Eines Tages, als Teresa wieder einmal in der Raumzeit spazieren ging, krabbelte ein kleiner, leuchtender Käfer an ihr vorbei, wie sie ihn noch nie zuvor gesehen hatte. “Hey, du, wollen wir ein Stück zusammen spazieren gehen?”, rief sie, aber der Käfer rief nur “geht nicht, ich kann nur in diese Richtung laufen!” und sauste weiter. “Seltsam,” dachte sie und ging weiter, wobei sie Ausschau nach weiteren Leuchtkäfern hielt. Als sie den nächsten Leuchtkäfer sah, verfolgte sie seinem Weg in der Raumzeit genau.
Anders als Teresa konnten Leuchtkäfer sich in der Raumzeit nicht bewegen wie sie wollten – wenn sie sich in der Raumrichtung bewegten, dann auch in Zeitrichtung. Wenn sie 5 Gitterlinien in Raumrichtung kreuzten, dann gingen sie genau eine Gitterlinie in Zeitrichtung. Egal wie lange Teresa die Leuchtkäfer beobachtete, sie fand nie einen, der sich anders bewegte. Und das brachte Teresa auf eine Idee: “Hey, wenn ich die Leuchtkäfer als Maßstab nehme, dann kann ich die Längen in Raumrichtung und die Längen in Zeitrichtung vergleichen.” Teresa zeichnete ihr Gitter neu, und zwar so, dass die Leuchtkäfer sich immer genau diagonal durch das Gitter bewegten. Ihr Gitter sah jetzt ganz ähnlich aus wie das von Anna:
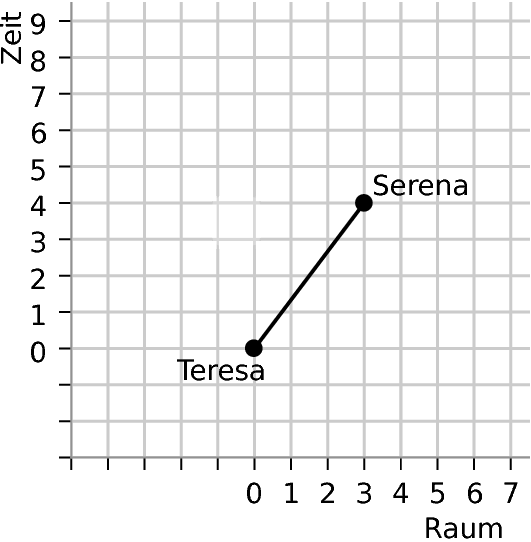
Auch Teresa hatte eine Freundin, Serena. Serena wohnte drei Einheiten (gemessen nach Tersas neuem Maßstab) in Raumrichtung und vier Einheiten in Zeitrichtung von Teresa entfernt. Serena legte ihre Zeitlinie (so ähnlich wie es auch Clara im Raum gemacht hatte) so, dass der Weg von Teresa zu ihr genau auf dieser Zeitlinie verlief. Wenn sie guckte, wie viel Zeit ihre Uhr für diesen Weg anzeigte, waren es aber nur etwas mehr als 2,6 Zeiteinheiten. Teresa und Serena rätselten lange, um das zu erklären.
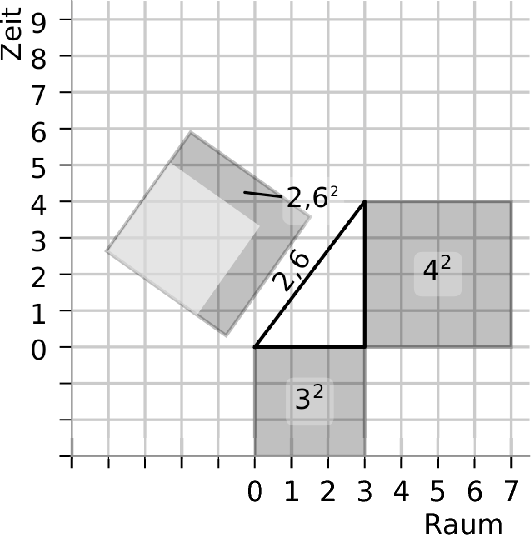
Schließlich trafen sie die weise Minkomite, die ihnen erklärte: “Es ist ganz einfach, das herauszufinden. Erst malst du ein Quadrat für die Entfernung in Teresas Raum-Richtung, dann eins für Entfernung in Teresas Zeitrichtung. Dann malst du ein Quadrat, das eine Fläche hat, die gleich der Differenz aus diesen beiden Quadraten ist, dessen Kantenlänge ist gleich der Zeit, die auf Serenas Uhr vergeht.”
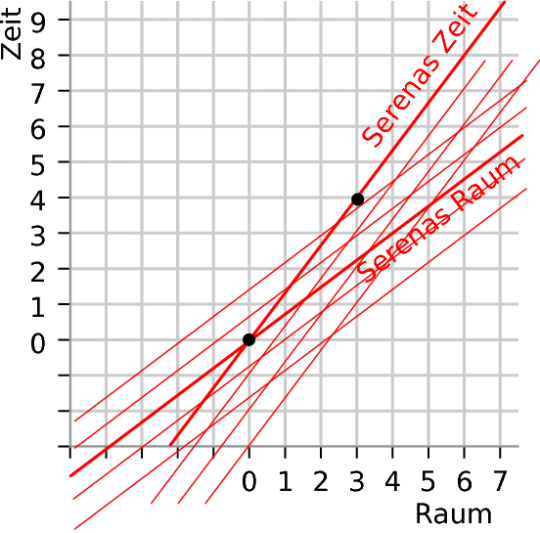
Damit Serena Entfernungen immer richtig messen konnte, musste sie natürlich auch ihre Raumachse passend drehen. Die Minkomite erklärte, dass sie dabei darauf achten musste, dass sich auch in ihrem Gitter die Leuchtkäfer immer in der gleichen Richtung bewegten: Ein Kästchen in Raumrichtung für jedes Kästchen in Zeitrichtung. Mit etwas Herumprobieren fand Serena heraus, dass sich das so bewerkstelligen ließ:
Von Teresa aus sah Serenas Gitter seltsam verzerrt aus, aber wenn Serena Dinge in ihrem Gitter maß, passte alles wunderbar zusammen.
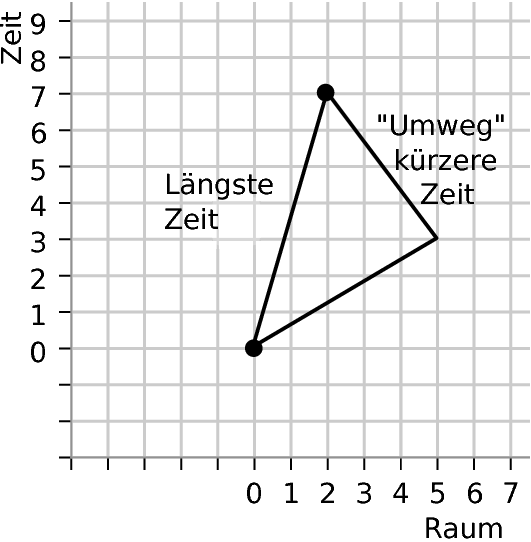
Auch Teresa und Serena liefen viel herum, aber natürlich in der Raumzeit. Sie fanden dabei etwas sehr merkwürdiges heraus: Wenn sie den direkten Weg zwischen zwei Punkten gingen, dann war der Wert auf der Uhr für den “direkten” Weg größer als auf jedem anderen Weg – vorausgesetzt, dass der andere Weg aus lauter Stücken bestand, die alle ebenfalls stärker in Raum- als in Zeitrichtung zeigten:
Der gerade Weg zwischen zwei Punkten war also nicht wie im Raum der kürzeste, sondern der mit der längsten Zeit.
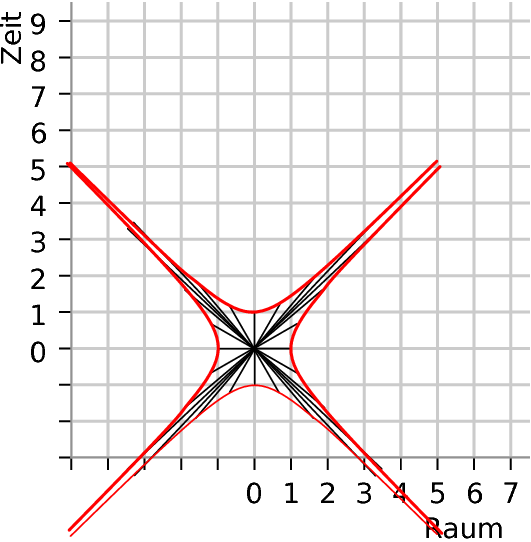
Als Teresa von Annas Entdeckung des “Kreis” hörte, wollte sie natürlich ausprobieren, ob sie etwas Ähnliches auch in der Raumzeit malen konnte. Weil Raum und Zeit sich ja unterschiedlich verhielten, gab es dafür zwei Möglichkeiten: Sie konnte entweder mehr in Raum- oder mehr in Zeitrichtung gehen – genau in der Leuchtkäferrichtung konnte sie dagegen nicht gehen, weil nach der Regel der Minkomite der Abstand in dieser Richtugn immer gleich null war. Zu ihrer Überraschung sah das Ergebnis aber nicht so hübsch aus wie bei Anna, sondern ergab eine seltsam gebogene Kurve aus vier Teilen:
PS: Was soll das?
Die Spezielle Relativitätstheorie ist ja oft verwirrend, das haben wir hier schön des öfteren gemerkt. Ein Teil der Verwirrung kommt daher, dass wir “Raum” und “Zeit” als ganz unterschiedliche Dinge auffassen, weil die Zeit uns als etwas erscheint, das zwangsläufig vergeht, der Raum dagegen ist etwas, in dem wir uns halbwegs frei bewegen können.Wenn man dagegen die Raumzeit der SRT als geometrisches Objekt auffasst, und sich erst einmal nicht um das “Vergehen “der Zeit kümmert (so wie im Blockuniversumsbild), dann kann man in meinen Augen viel klarer sehen, wie die SRT funktioniert. (Anmerkung: beim Einzeichnen von Serenas Koordinatensystem war ich nicht ganz genau, ich hoffe, das stört niemanden.) Statt das berühmte Zwillingsparadoxon mühsam aufzulösen, indem man den Weg zweier Raumschiffe in der Raumzeit verfolgt und die Stücke mit Hilfe von komplizierten Lorentz-Transformationen und allem möglichen berechnet, kann man sich das ganze ganz einfach geometrisch veranschaulichen: Ein gerader Weg zwischen zwei Punkten hat eine andere Länge als einer, der einen “Umweg” geht. Im Raum ist der Umweg natürlich länger (mathematisch nennt man das die “Dreiecksungleichung”); in der Raumzeit ist der Umweg aber kürzer als der direkte Weg (das ist das berühmte “Prinzip der maximalen Eigenzeit”). Sinn dieses Textes ist also letztlich nur, rein geometrisch zu veranschaulichen , wie sich Raum und Raumzeit unterscheiden und wo die Gemeinsamkeiten sind. Ob’s eurer Anschauung am Ende weiterhilft, weiß ich natürlich nicht, ihr könnt gern einen Kommentar hinterlassen.






Kommentare (625)