To see a World in a Grain of Sand
And a Heaven in a Wild Flower,
Hold Infinity in the palm of your hand
And Eternity in an hour.
William Blake
In der Allgemeinen Relativitätstheorie hat man es oft mit seltsamen Unendlichkeiten zu tun: In Schwarzen Löchern gibt es Singularitäten (und Ereignishorizonte), und auch unser Universum als Ganzes ist (vermutlich) räumlich und zeitlich unendlich. Damit zu hantieren ist nicht ganz einfach, weil man meist keine unendlich großen Papiere oder Computerbildschirme hat und deswegen nicht alles übersichtlich darstellen kann. Es gibt aber einen Trick, mit dem man sich einen Überblick auch über unendliche Raumzeiten verschaffen kann: Penrose-Diagramme. Die sind leider ein bisschen knifflig zu verstehen (ich gebe zu, ich habe mich damit lange sehr schwer getan), deswegen schauen wir mal ganz in Ruhe, wie das geht (so habe ich’s dann auch verstanden; leider haben diese Erklärungen hier es nicht mehr in mein Buch geschafft, das war eh schon zu dick…)
Wir denken uns erst einmal ein ganz einfaches Universum, das aus der speziellen Relativitätstheorie (SRT). Unser Universum ist statisch, da gab’s keinen Urknall oder sowas, und die Raumzeit ist auch nicht gekrümmt.Unser Universum ist unendlich groß und hat schon immer existiert und das wird es auch für alle Zeit tun.
Wir machen es uns erstmal einfach und denken uns das Universum räumlich eindimensional – es gibt also nur eine Linie, entlang der wir uns bewegen können. Jeden Punkt in unserem Universum können wir dann mit zwei Zahlen kennzeichnen, eine für den Ort (x), eine für die Zeit (t). So etwa könnte man einen Ausschnitt dieses Universums darstellen:

Von Karl Hilpolt – Eigenes Werk, CC BY-SA 4.0, Link
In unserem Universum gelten die Regeln der SRT – Licht bewegt sich immer mit Lichtgeschwindigkeit und nichts ist schneller als das Licht. (Nebenbemerkung: Dass sich nichts schneller als das Licht bewegen kann, kann man mit etwas Geschick direkt aus der Konstanz der Lichtgeschwindigkeit folgern, fragt Isaac, wie das geht…) In unserem Diagramm messen wir Zeiten in Sekunden und Entfernungen in Lichtsekunden (300000km), dann legt das Licht in einer Zeiteinheit auch eine Längeneinheit zurück, so dass Lichtsignale im Diagramm immer unter 45 Grad verlaufen. (Im Bild sind kleine Kegel eingezeichnet, die symbolisieren, dass das Licht sich in unterschiedliche Raumrichtungen ausbreiten kann, aber im Moment lassen wir unser Universum noch räumlich eindimensional.)
So ein Diagramm ist ja ganz nett, hat aber einen Nachteil: Wenn unser Universum unendlich groß ist und unendlich lange existiert hat, dann können wir nicht den ganzen Raum oder die ganze Geschichte des Universums aufzeichnen, es sei denn, wir haben ein unendlich großes Blatt Papier. Gesucht ist deshalb eine Möglichkeit, die gesamte Raumzeit des Universums auf einem endlichen Bereich abzubilden. Das geht natürlich logischerweise nur dann, wenn wir einige Bereiche sehr stark zusammenquetschen.
Dass das prinzipiell aber möglich ist, kennt ihr alle aus dem Zeichenunterricht in der Schule (Diese Analogie habe ich vom backreaction-Blog). Stellt euch unendlich lange Bahnschienen vor (auf einer flachen und unendlich großen Erde). Wenn ihr diese vom Boden aus anschaut, sieht das etwa so aus:

Von Andrzej O – Eigenes Werk, CC BY-SA 3.0, Link
Klar, je weiter die Bahnschienen weg sind, desto enger wird alles zusammengequetscht, aber im Prinzip sind die gesamten Bahnschienen zu sehen (auf der flachen Erde, wohlgemerkt, und natürlich mache ich mir als Theoretikerin keine Gedanken über so Dinge wie Lichtabsorption in der Luft oder sonstiges praktisches Zeugs).
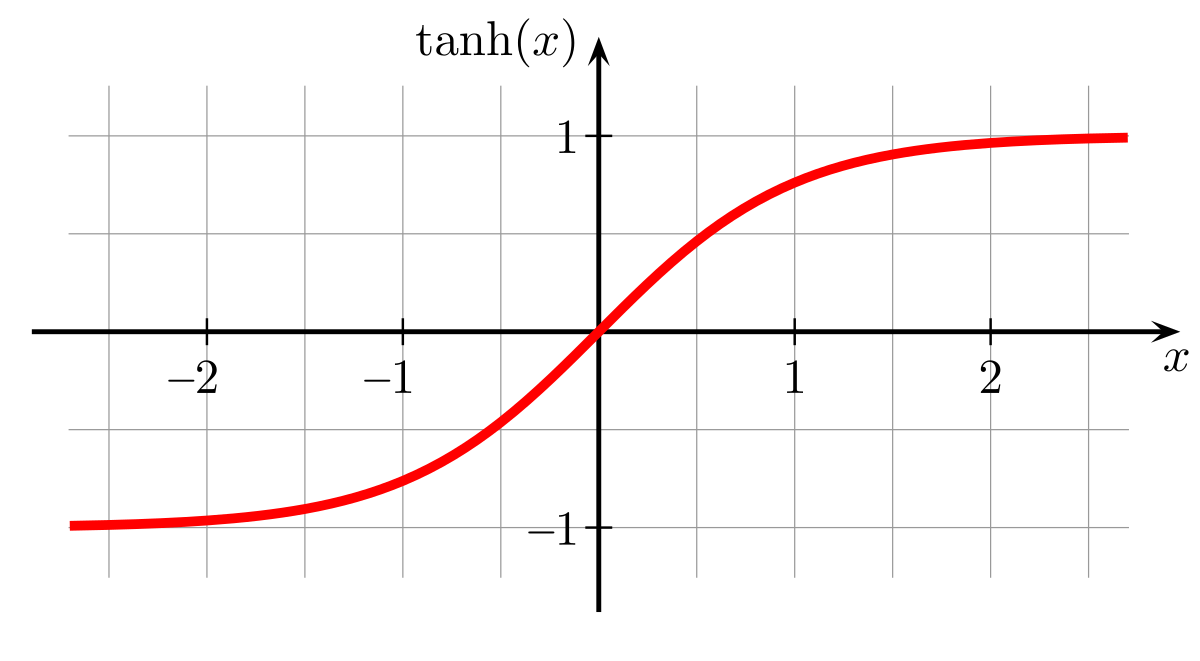
Wir können uns auch einen mathematischen Trick überlegen, wie wir zunächst mal eine Dimension (beispielsweise den Raum x) auf einen endlichen Bereich abbilden können. Dazu können wir beispielsweise diese Funktion (mathematisch ein tangens hyperbolicus) nehmen:
Von Geek3 – Eigenes Werk, CC BY-SA 3.0, Link
Auf der horizontalen Achse sehen wir die tatsächliche Raumkoordinate, auf der vertikalen sehen wir, wie wir diese Raumkoordinate auf einen Wert zwischen -1 und 1 abbilden können. Alles bei Werten größer als 2 oder 3 wird dabei natürlich extrem gestaucht, aber es haben nie zwei unterschiedliche x-Werte exakt denselben Wert unserer neuen Koordinate.
Wir können jetzt also mit diesem Verfahren unser Koordinatensystem auf einen endlichen Bereich abbilden. So würde das aussehen:

Für unsere Zeitkoordinate können wir das genauso machen, dann bekommen wir etwa so ein Bild:

Erinnert ein bisschen an Bilder, die man mit einem Fischaugen-Objektiv macht (dieser Vergleich zu Penrose-Diagrammen wird auch hier gezogen):

By Danielteolijr – Own work, CC BY-SA 4.0, Link
So, damit haben wir also erst einmal einen Trick gefunden, wie wir ein unendlich großes (wenn auch eindimensionales) und unendlich lange existierendes Universum auf einer endlichen Fläche abbilden können. Einiges wird dabei natürlich unendlich stark komprimiert, aber wie wir nachher sehen werden, schadet das nichts, wenn es darum geht, so Dinge wie Schwarze Löcher mit Diagrammen zu erfassen.
Mein schönes Gitter von oben ist aber selbst noch nicht so gut geeignet, um ein Universum darzustellen, in dem die SRT gilt. Das seht ihr leicht, wenn ihr den Weg eines Lichtstrahls einzeichnet. Ein Lichtstrahl legt ja in einer Zeiteineinheit eine Längeneinheit zurück (Eine Lichtsekunde pro Sekunde), muss also von einem Kreuzungspunkt der Gitterlinien zum nächsten laufen. Nehmen wir an, ich sende ein paar Lichtstrahlen am Ort x=0 aus. So sehen deren Verläufe dann aus:
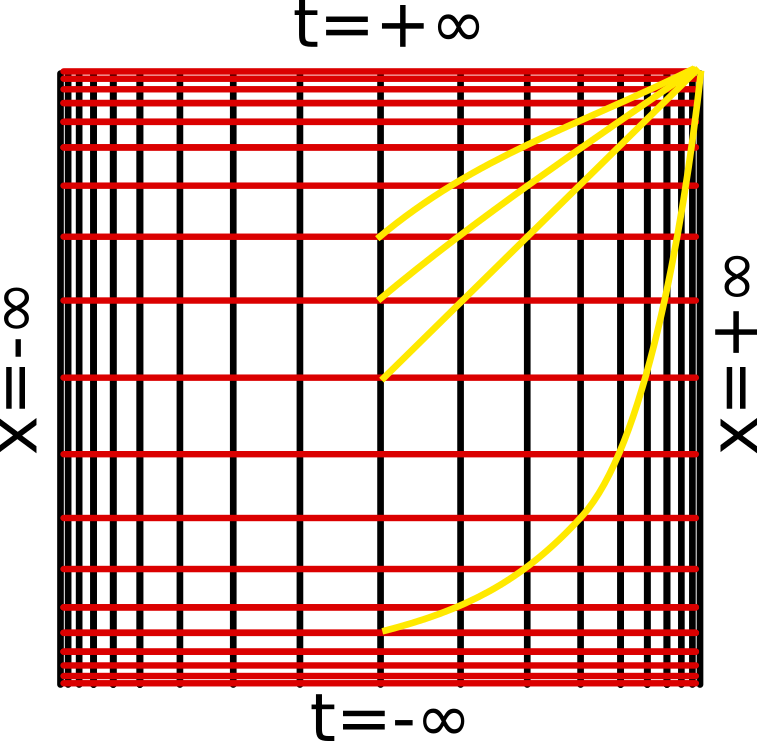
Je nachdem, wann ich die Lichtstrahlen aussende, sehen ihre Linien also unterschiedlich aus, mal sind sie nach oben, mal nach unten gebogen, mal gerade. Die schöne Eigenschaft von Raumzeit-Diagrammen in der SRT, dass Lichtstrahlen immer unter 45 Grad verlaufen, habe wir damit also verloren.
Wir können auch noch auf andere Weise sehen, dass unser Diagramm nicht wirklich hilfreich ist, wenn wir uns nämlich über unterschiedliche Arten von Unendlichkeiten Gedanken machen. Ich meine damit nicht so Dinge wie Aleph 1 und ähnliches, darüber sollen die Mathermatikerinnen nachdenken. Aber in der RT gibt es auch verschiedene Unendlichkeitsarten, die damit zusammenhängen, dass die Lichtgeschwindigkeit die Obergrenze für alle Bewegungen darstellt.
Nehmen wir mal ganz bescheiden an, wir (bei Koordinate x=0) wären der Mittelpunkt des Universums, so wie ich das bisher in den Bildern immer dargestellt habe.
Welche Bereiche des Universums können wir erreichen? Da wir nicht schneller als mit Lichtgeschwindigkeit unterwegs sein können, können wir einen Lichtstrahl in unser Diagramm einzeichnen. Dazu nehmen wir das einfache Minkowski-Diagramm von oben und zeichnen Lichtsignale ein, sowohl nach links als auch nach rechts und auch welche in die Vergangenheit (dazu kommen wir gleich):
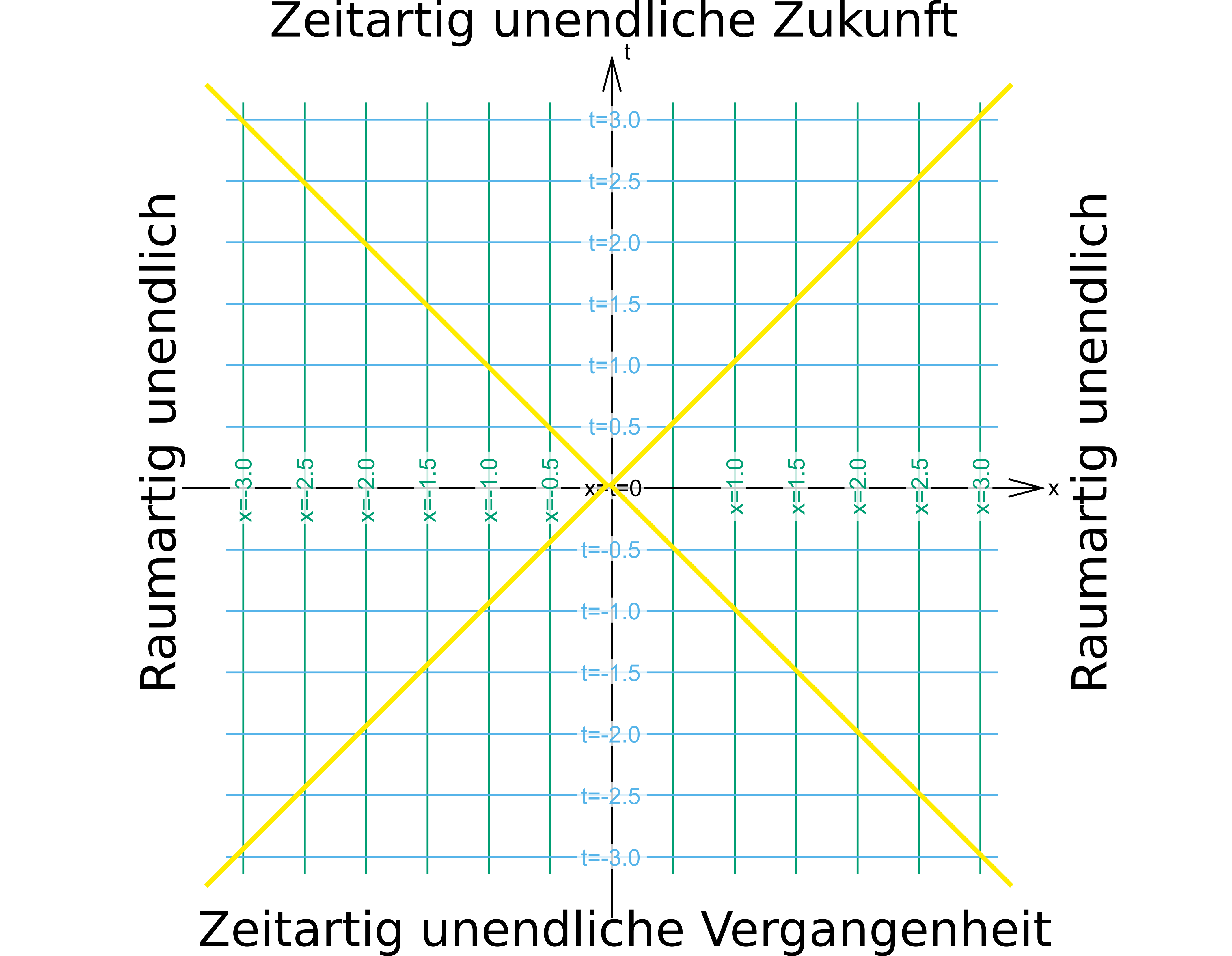
Modifiziert nach Vorlage von Karl Hilpolt – Eigenes Werk, CC BY-SA 4.0, Link
Alles, was im Diagramm oben innerhalb der beiden diagonalen Linien liegt, sind Bereiche, die wir erreichen können, wenn wir langsamer als das Licht unterwegs sind. Wenn wir unendlich weit in die Zukunft gehen, können wir schließlich jeden Raumbereich erreichen, aber wir brauchen dafür auf jeden Fall länger als ein Lichtstrahl weil wir ja nie die Lichtgeschwindigkeit erreichen. Diesen Bereich in der Zukunft nennen wir “zeitartig unendlich”. (Es gibt sogar einen SF-Roman mit dem Titel “timelike infinity”.) Für die vergangenheit gilt das Gleiche: Man könnte uns beispielweise mit einem raunfahrzeug von jedem Punkt erreichen, der zwischen den beiden unteren Licht-Linien liegt.
Es gibt aber auch Bereiche der Raumzeit, die wir nie erreichen können, nämlich alles was rechts und links liegt. Um dorthin zu kommen, müssten wir schneller als das Licht sein. Diese unendlich weit entfernten Bereiche nennen wir “raumartig unendlich”, sie sind von uns “kausal getrennt” – dorthin können wir kein Signal schicken, und von dort können wir auch keins empfangen. Theoretisch könnten wir zwischen raumartig unendlich “links” und “rechts” unterscheiden, aber in der Realität, wo wir mehr als eine Dimension haben, sind diese Bereiche natürlich miteinander verbunden.
Wir haben also im Moment die raumartige Unendlichkeit und zwei zeitartige Unendlichkeiten, eine für die vergangenheit, eine für die Zukunft. Das ist aber noch nicht alles. Wenn wir nämlich einen unserer Lichstrahlen von eben verfolgen (egal welchen), sehen wir, dass der noch eine andere Unendlichkeit erreicht. Alles, was der Lichtstrahl überstreicht, ist nicht raumartig, denn wir können ja ein Lichtsignal dorthin schicken (das tun wir ja gerade). Es ist aber auch nicht zeitartig, denn der Lichtstrahl überholt ja jedes Signal, das wir langsamer als mit Lichtgeschwindigkeit aussenden. Egal wann und wie schnell wir ein objekt mit weniger als Lichtgeschwindigkeit aussenden, es wird schließlich von unserem Lichtstrahl überholt werden. Damit gibt es also noch eine dritte Art von Unendlichkeit, “lichtartig unendlich”. Von der gibt es auch wieder zwei Varianten, eine für die Vergangenheit, eine für die Zukunft. Wir können das schematisch etwa so darstellen:
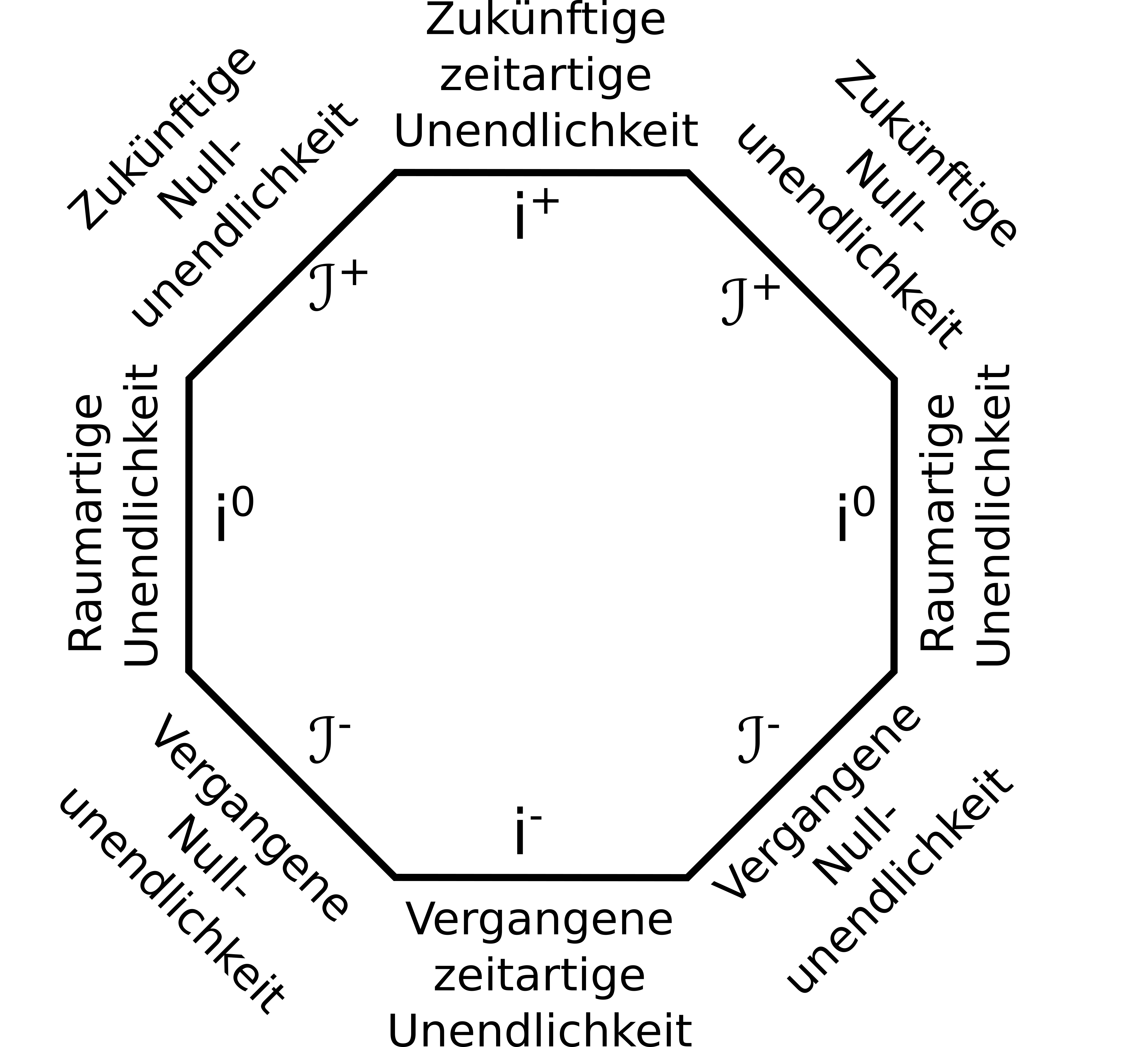
Dabei habe ich die Unendlichkeiten mit ihren gebräuchlichen Namen versehen – zeitartige und raumartige Unendlichkeit hatten wir schon, die lichtartigen nennt man aber “Nullunendlichkeiten”, weil die Raumzeitlänge entlang eines Lichtstrahls immer gleich Null ist. (Wer das verstehen will, guckt hier). Die Unendlichkeiten werden auch gern mit Symbolen gekennzeichnet, die kleinen “i” stehen für raumartig (mit Index 0), vergangen zeitartig (index -) oder zukünftig zeitartig (Index +). Die Nullunendlichkeiten, also die, die von Lichtstrahlen erreicht werden, werden mit einen geschwungenen i dargestellt, einen Skript-I oder kurz “scri”. Von denen gibt es auch zwei, eine für die vergangenheit, eine für die Zukunft.
Jetzt haben wir also ein schönes Diagramm für die Unendlichkeiten, aber ihr seht schon, dass das Diagramm auch nicht die gewünschte Eigenschaft hat, dass alle Lichtlinien unter 45 Grad verlaufen. Die Lichtstrahlen landen ja alle bei scri-plus, aber einer der im Diagramm knapp unterhalb von i+ ausgesandt wird, muss dann natürlich sehr flach verlaufen.
Damit alles passt, müssen wir das Diagramm noch etwas verändern: Wir schrumpfen alle Unendlichkeiten (außer den Nullunendlichkeiten) auf einen Punkt zusammen (“infinity in the palm of your hand…”). So sieht das Ergebnis dann aus:

Von Karl Hilpolt – Eigenes Werk, CC BY-SA 4.0, Link
Dabei sind die Schriftarten für die i’s und Scris etwas anders, aber ihr erkennt hoffentlich die Logik wieder. (Die griechischen pis ignorieren wir einfach…)
Damit haben wir ein echtes “Penrose-Diagramm” gebastelt. Wie liest man so etwas? Die blauen und grünen Linien sind Linien mit konstanten koordinaten. In der Mitte haben wir horizontal die x-Achse bei t=0, darunter, bei -0.5, sehen wir alle Ereignisse, die zu dieser Zeit gleichzeitig waren (also dieselbe zeitkoordinate haben) usw. Die von oben nach unten verlaufenden Linien sind Linien mit konstanter Ortskoordinate. Ein Objekt, das seit Anbeginn der Zeit bei x=0.5 ist und sich nicht bewegt, folgt also im Diagramm einer nach rechts gekrümmten Linie.
Folgen wir als nächstes der orangenen Linie (die unten im Diagramm leicht rausragt, das ist aber nur ein kleiner Fehler in der Zeichnung). Da fliegt irgendeine Objekt im Diagramm also mit weniger als Lichtgeschwindigkeit (die Linie läuft ja nicht unter 45 Grad) von links nach rechts. (Es sieht so aus, als würde es erst nach links fliegen, aber tatsächlich kreuzt es Linien mit konstanter Ortskoordinate immer nur von links nach rechts, danke Christian für die Korrektur. ) Was es ganz oben, bei i+ tut, ist schwer zu erkennen, weil da alles so verzerrt ist (ähnlich wie beim Fischauge). Sendet unser Objekt Lichtsignale aus, dann verlaufen die unter 45 Grad.
So weit so gut. Allerdings ist unser Universum ja nicht bloß räumlich eindimensional, sondern dreidimensional. Wie können wir das umsetzen?
Machen wir erstmal den Schritt von einer zu zwei Raumdimensionen, das kann man dann noch halbwegs zeichnen. Da können wir (auch in einem unendlichen Universum) einen Punkt als Koordinatenursprung wählen und dann jeden anderen punkt dadurch bestimmen, dass wir den Abstand zu diesem Ursprung nehmen und einen Winkel, der uns sagt, in welche Richtung wir gehen müssen (nennt man auch Polarkoordinaten):
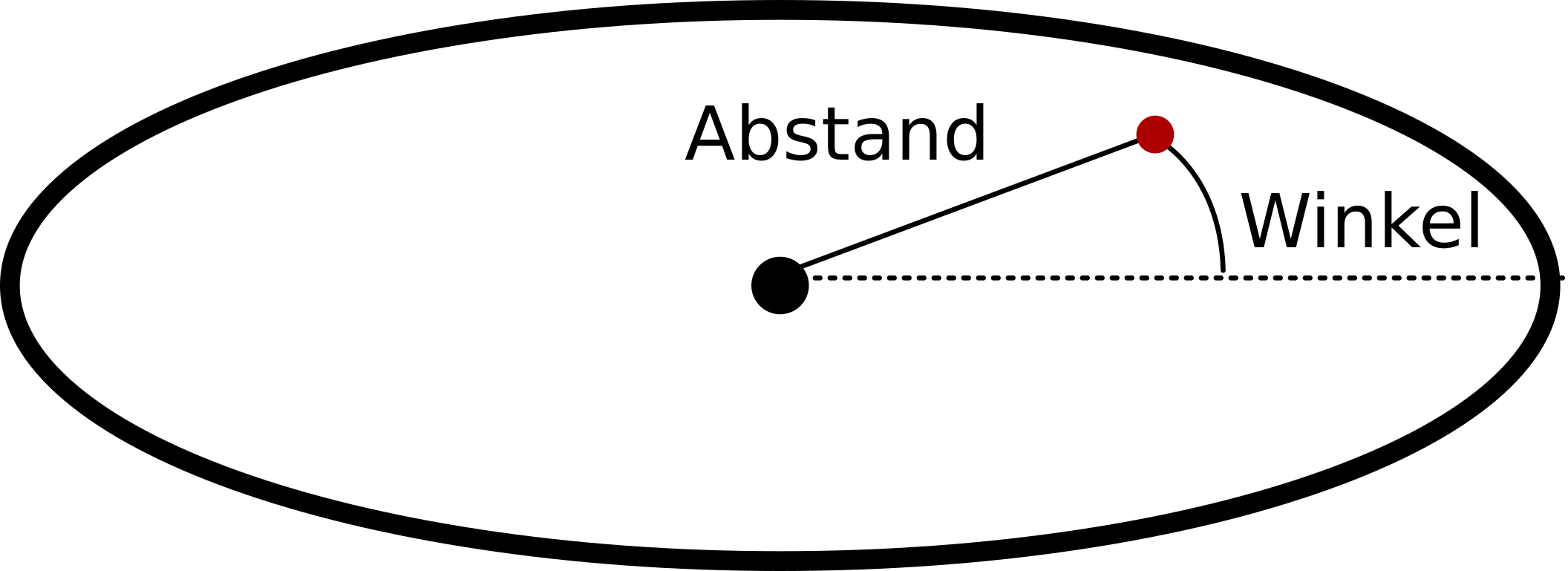
Wir können jetzt genau wie vorher den Abstand so umdefinieren, dass alles auf eine endliche Fläche passt, indem wir alles zum Rand hin immer dichter werden lassen (erinnert an Bilder von MC Escher, ich füge hier aber keins ein, da sind die Escher-Erben ziemlich unentspannt…), etwa so:
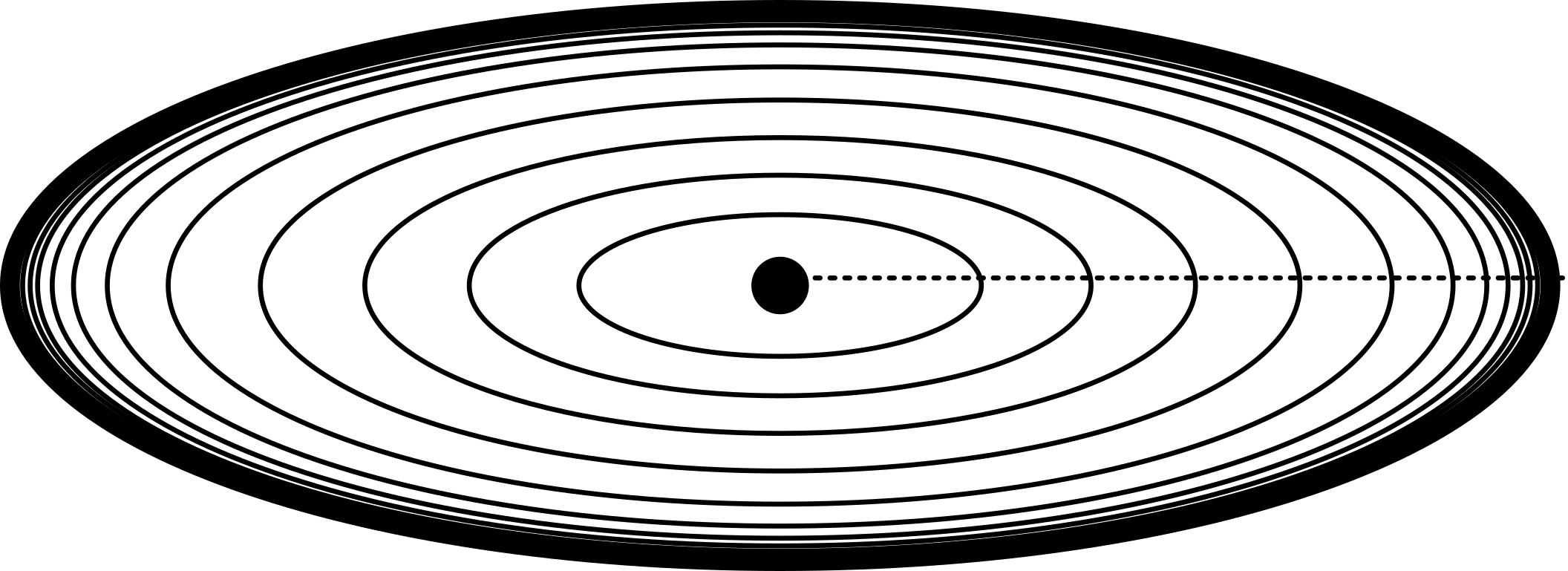
Und jetzt fügen wir wieder eine Zeitkoordinate hinzu, dann bekommen wir etwas, das aussieht wie zwei aufeinander gestapelte Kegel (zugegeben, bei der Perspektive war ich etwas unsauber):

Dabei habe ich wieder die Unendlichkeiten markiert: die untere Spitze ist negativ zeitartig unendlich, die obere positiv zeitartig unendlich, der Rand des Kreises in der Mitte ist die raumartige Unendlichkeit und die Kegelmäntel sind die beiden Nullunendlichkeiten. Irgendwie hübsch, aber auch nicht so richtig toll übersichtlich. Deshalb ignoriert man dann typischerweise den Winkel und stellt alles nur über den Abstand dar, so dass jeder Punkt in Wahrheit einem Kreis entspricht (r=0 kennzeichnet also den Mittelpunkt der Kreise oben im Bild):
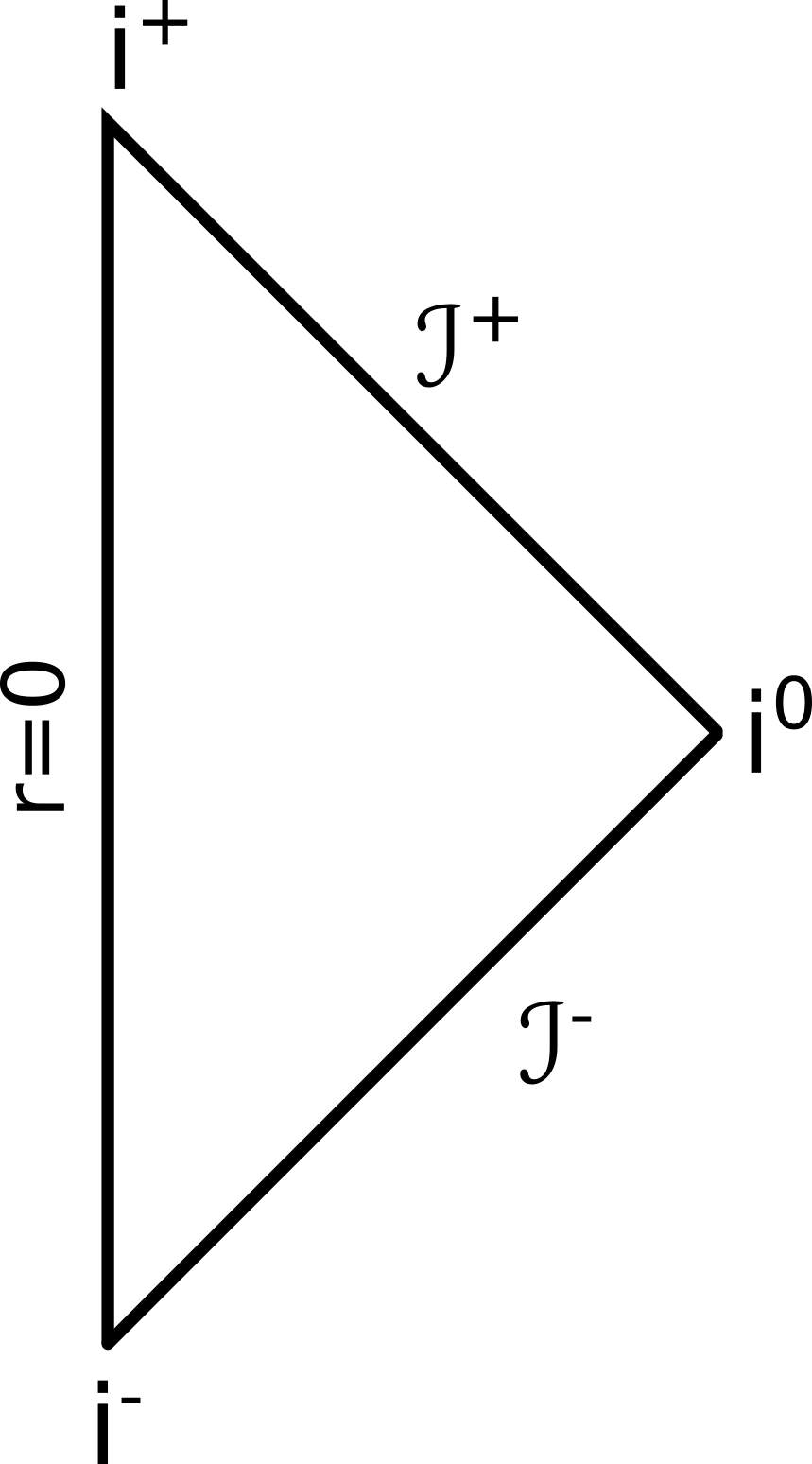
In drei Dimensionen geht das genauso – wir unterschlagen dann zwei Winkel (Längen- und Breitengrad), so dass jeder Punkt in unserem Diagramm räumlich einer Kugeloberfläche entspricht.
Wie ihr seht, ist das entstehende Diagramm sehr ähnlich zu dem, das wir oben für die eine Raumdimension gezeichnet haben; es ist sozusagen die Hälfte davon. Man muss hier ein bisschen aufpassen, wenn man sich zum Beispiel vorstellt, wie ein Lichtsignal verläuft. Nehmen wir an, ich schwebe irgendwo (nicht bei r=0) und sende ein Lichtsignal (genau entlang der Richtung zum Mittelpunkt) aus. Das erreicht dann irgendwann diesen Mittelpunkt und entfernt sich dann wieder, das würde also so aussehen:
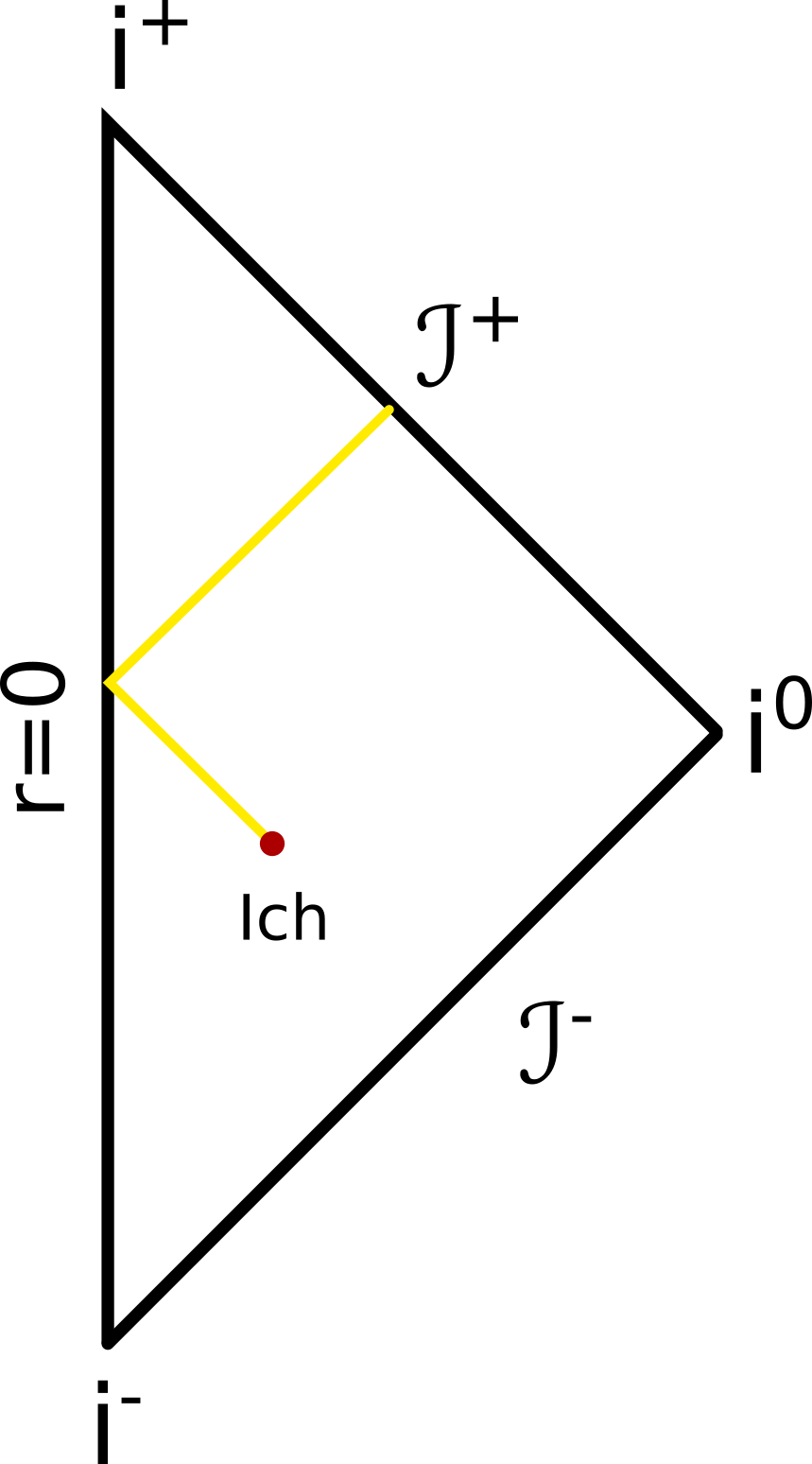
Man kann solche Diagramme also auf zwei Arten zeichnen – mit “normalen” (kartesischen) Koordinaten, die auch negativ werden können, oder mit Polarkoordinaten, die Null, aber nicht negativ sein können. Für die normale, leere Raumzeit unseres Universums ergibt sich im einen Fall ein auf die Spitze gestelltes Quadrat (das Bild oben), im anderen Fall ein Dreieck. Das heißt aber ganz ausdrücklich nicht, dass ihr immer dann, wenn ihr ein quadratisches Penrose-Diagramm seht, annehmen könnt, es wäre in kartesischen Koordinaten gezeichnet – meist ist das nämlich nicht der Fall. In der Praxis werden Penrose-Diagramme fast immer nur in Polarkoordinaten gezeichnet, so dass r immer größer oder gleich Null ist. Trotzdem können die Diagramme so (oder so ähnlich) aussehen wie das Quadrat von oben, aber das ist, wie es aussieht, eine andere Geschichte und soll ein andermal erzählt werden – im zweiten Teil (wieso werden meine Blogartikel immer so lang???), in dem wir versuchen zu verstehen, wozu solche Penrose-Diagramme eigentlich gut sind und in denen wir dann auch einen Blick auf Schwarze (und Weiße!) Löcher, Ereignishorizonte und ähnliche Dinge werfen.






Kommentare (4)