Im ersten Teil dieses Artikels habe ich euch versucht, die Logik von Penrose-Diagrammen zu verklickern. Heute gucken wir, was wir damit anfangen können.
Zur Erinnerung nochmal das Penrose-Diagram einer “leeren”, ungekrümmten Raumzeit mit ihren unterschiedlichen Unendlichkeiten:
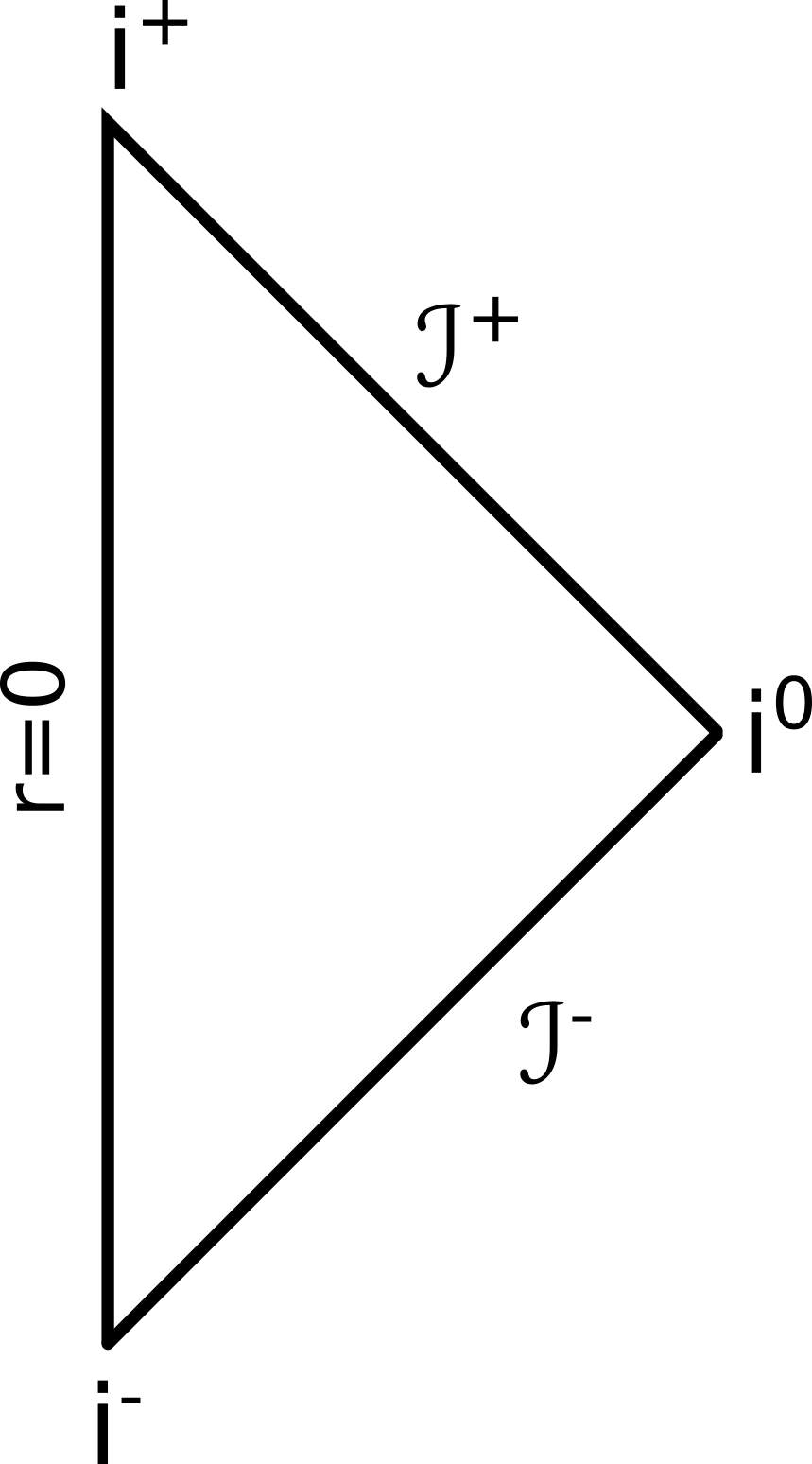
Nehmen wir jetzt an, wir haben ein Schwarzes Loch in unserer Raumzeit. Schwarze Löcher (kurz SL) haben ja einen Ereignishorizont, einen Punkt ohne Wiederkehr. (Eigentlich ist der Punkt eine Kugeloberfläche, aber in unserem Penrose-Diagramm wird ja jede Kugeloberfläche auf einen Punkt abgebildet, weil man sonst mehrdimensional zeichnen müsste – erinnert euch an den Kegel vom letzten Mal). Nehmen wir an, dieser Ereignishorizont läge bei einem Wert von r=1 (Achtung: ich habe die genaue Linie nicht gerechnet, sondern nur schematisch eingezeichnet):
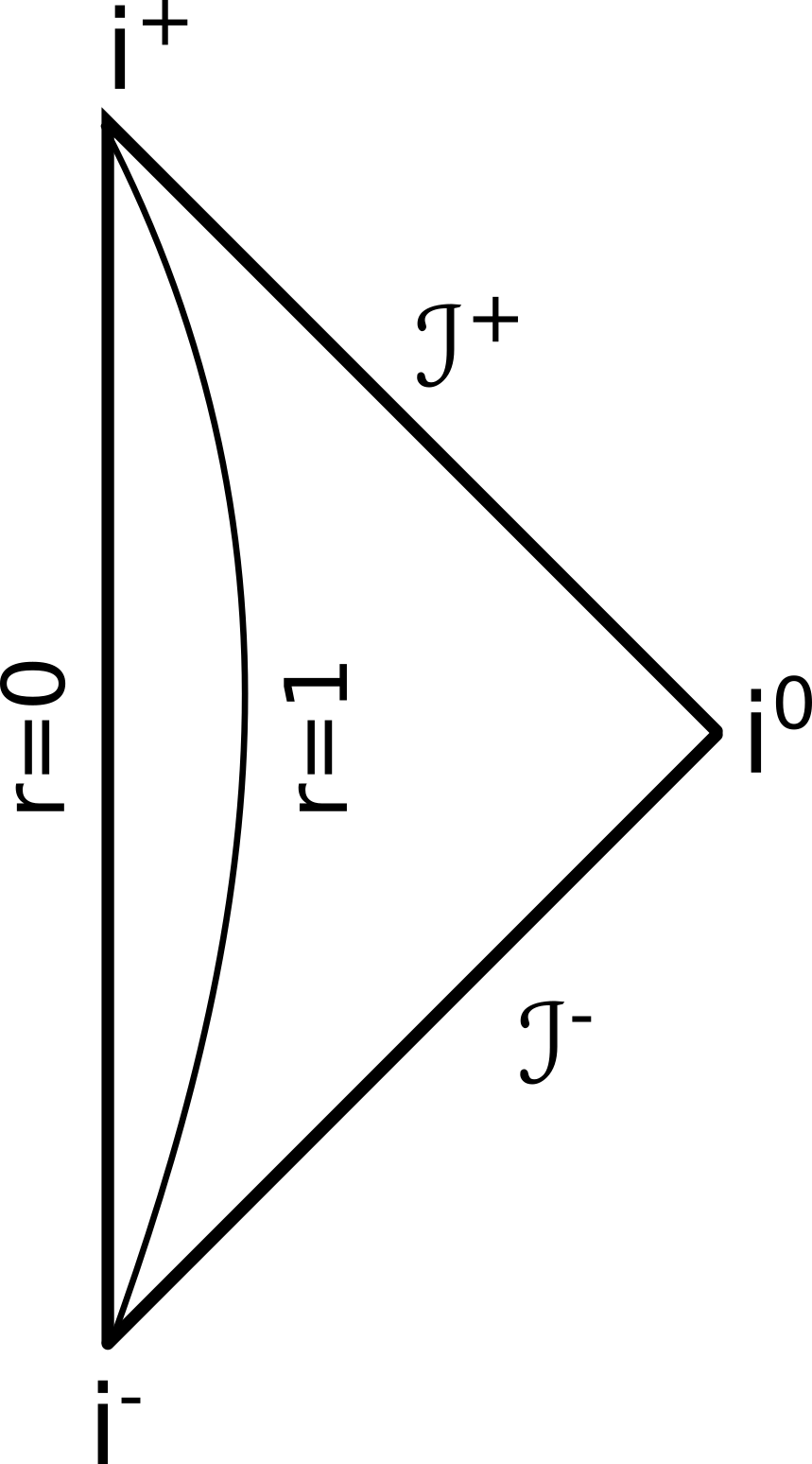
Also ist der Bereich links von r=1 das Innere des SL, die Linie ist der Ereignishorizont und rechts davon ist außen? Nein, leider funktioniert das so nicht. Ihr erinnert euch sicher, dass eine zentrale Eigenschaft unserer Diagramme sein sollte, dass Lichtstrahlen immer unter 45 Grad verlaufen. Wenn ich am Ereignishorizont bin und einen Lichtstrahl aussende, dann kann dieser den Ereignishorizont aber ja nicht verlassen – Schwarze Löcher sind bekanntlich schwarz. Ein solcher Lichtstrahl würde in diesem Diagramm also entlang der r=1-Linie verlaufen (das Licht ist quasi am Ereignishorizont eingefroren). [Nebenbei, damit sich niemand wundert: Ich kann natürlich nicht am Ereignishorizont statisch sitzen und Lichtstrahlen aussenden, aber ich könnte in ein SL hineinfallen und genau in dem Moment, wo ich am Ereignishorizont bin, meine Lampe anknipsen.]
Wenn wir am Ereignishorizont sind, können wir einen Lichtstrahl entweder nach außen schicken, dann bleibt er am Horizont eingefroren. Oder wir schicken ihn nach innen, dann stürzt er ins Innere des Schwarzen Lochs. Außerdem soll unser Lichtstrahl im Diagramm unter 45 Grad verlaufen (nach links oder rechts). Wie müssen wir einen Ereignishorizont zeichnen, wenn ein nach Außen laufender Lichtstrahl immer an diesem Horizont bleiben soll, ein nach innen laufender ins Innere stürzen soll, und kein Lichtstrahl jemals unter 45 Grad aus dem SL entkommen kann?
Richtig, der Ereignishorizont muss unter 45 Grad im Diagramm verlaufen. Versuchen wir mal, das in unser Diagramm einzuzeichnen (wobei ich den unteren Teil weglasse, darüber müssen wir uns gleich noch Gedanken machen:)

Alles Licht, das (unter 45 Grad) nach links auf den Ereignishorizont zuläuft, landet schließlich hinter dem Horizont (da gehts auch nicht immer weiter, egal, was Udo dazu sagt, dann kommt nämlich die Singularität…). Alles Licht das nach rechts (also nach außen) am Horizont ausgesandt wird, bleibt auf der roten Linie am Ereignishorizont. So weit, so gut. Verfolgen wir mal das Licht weiter, das in das Schwarze Loch reinstürzt. Was wird aus dem? Es landet wie gesagt in der Singularität. Da das Licht im Diagramm immer unter 45 Grad verläuft, müssen wir die Singularität so einzeichnen, dass alle Linien, die vom Ereignishorizont aus nach Innen laufen, schließlich dort landen. Das sieht dann so aus:

Zugegeben, die wellige Linie für die Singularität hätte ich auch anders zeichnen können, das ist letztlich Konvention. Wichtig ist nur, dass alle Linie, die vom Ereignishorizont bei r=1 ausgehen, diese Linie zwangsläufig erreichen. (Anmerkung: Die Linie so zu zeichnen, hat aber den Charme, dass sich in gewisser Weise innerhalb des Ereignishorizonts Raum und Zeit umkehren – oben ist nicht mehr die zeitartige Unendlichkeit, sondern die Singularität, Wege von r=1 nach r=0 zeigen nach oben, so wie außerhalb des SL Linien mit konstanter Ortskoordinate nach oben führen. Das ist insofern nett, als es widerspiegelt, was passiert, wenn man ein SL in Schwarzschild-Koordinaten beschreibt. Das sehen wir gleich noch genauer.)
Was ist nun mit dem unteren Teil des Diagramms? Wenn unser SL schon immer existiert haben soll, dann müssen alle Photonen, die wir in Richtung des SL schicken, den Ereignishorizont erreichen. Also müssen wir hier eine Begrenzungslinie haben, die unter 45 Grad verläuft. Damit bekommen wir als Endergebnis das hier als Penrose-Diagramm eines Universums mit einem ewig existierenden SL:

Das mag etwas verwirren – warum habe wir unten nochmal einen Ereignishorizont? Aber schauen wir alles mal in Ruhe an: Jeder Lichtstrahl von aus der vergangenen Nullendlichkeit (script-I-Minus) in Richtung SL geschickt wird, landet schließlich bei der Singularität. Das ist soweit richtig. Auch jeder Lichtstrahl, der innerhalb des Quadrats (also von einem nicht-unendlichen Raumzeitpunkt aus) aufs SL geschickt wird, landet dort. Wenn wir uns aber fragen, wann die Lichtstrahlen (von außen betrachtet) dort eintreffen, dann geschieht dies bei Zeitkoordinate Unendlich (weil ja die Zeitdilatation am Ereignishorizont unendlich groß ist). Die obere r=1-Linie ist also eine Linie, bei der die Zeit positiv unendlich ist. Die untere Linie ist dann eine Linie, bei der die Zeit negativ unendlich ist. Es wird vermutlich deutlicher, wenn man nochmal Linien mit konstanten Raum- und Zeitkoordinaten einzeichnet:
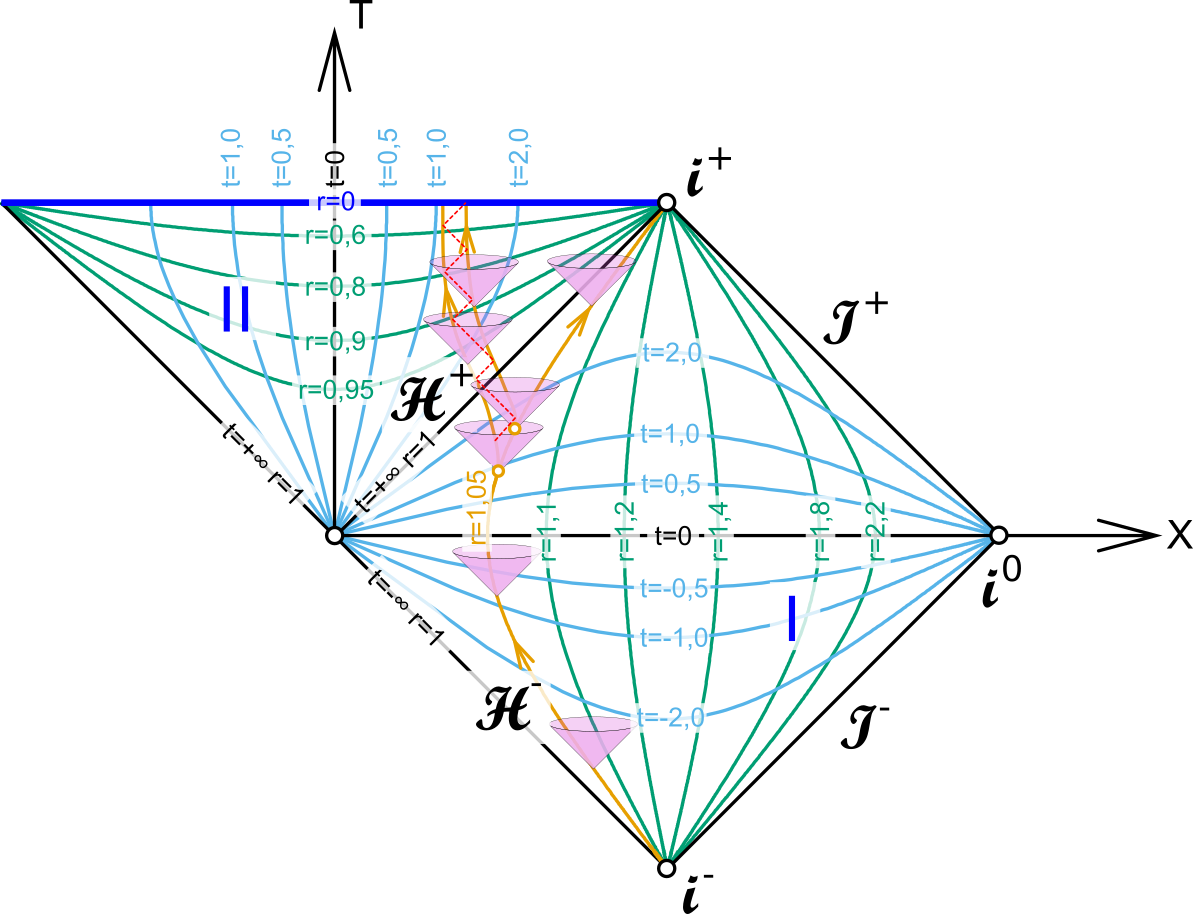
Modifiziert von einer Vorlage von Karl Hilpolt – Own work, CC BY-SA 4.0, Link
Ihr seht ganz klar, dass das Diagramm (anders als Gallien) in zwei Teile zerfällt, mit den beiden römischen Ziffern I und II gekennzeichnet. Bereich I ist das Universum außerhalb des SL. Die grünen Linien sind Linien mit konstanter Ortskoordinate, die blauen Linien die mit konstanter Zeitkoordinate (es gibt also eine Beobachterin, für die alles auf dieser linie gleichzeitig erscheint).
Links sehen wir eine orangefarbene Linie bei r=1,05. Hier befindet sich jemand dicht über dem Ereignishorizont (gekennzeichnet mit Skript-H-plus) bei konstantem Wert von r (mag aber das SL dabei umkreisen, wobei eine stabile Umlaufbahn nicht existiert, da müssen schon die ganze Zeit die Motoren laufen). Diese Person sendet bei t=1 eine Sonde aus, die ins SL stürzt und dabei (rot gestrichelte Linien) Signale mit einer zweiten, etwas später ausgesandten Sonde austauscht. Die beiden Sonden überqueren den Ereignishorizont. Von außen gesehen ist dabei die Zeitkoordinate unendlich – aber für die Sonden vergeht nur eine endliche Zeit. An den roten Signalen sieht man auch wieder, wie praktisch diese Darstellung ist, es ist sofort klar, dass man kein Signal vom Ereignishorizont nach draußen schicken kann.
Im Innern des SL sind es jetzt Linien mit konstanter Ortskoordinate, die horizontal (aber gekrümmt) sind, Linien konstanter Zeitkoordinate laufen von unten nach oben. Ich hatte ja oben schon angemerkt, dass Orts- und Zeitkoordinate im Inneren eines SL gewissermaßen die Rollen tauschen – außerhalb eines SL läuft eine Weltlinie zwangsläufig in die Zukunft, innerhalb des SL verläuft sie zwangsläufig zur Singularität.
Verwirrend an diesem Diagramm mag erscheinen, dass der Bereich I ganz ähnlich aussieht wie unser Penrose-Diagramm vom letzten Mal, bei dem wir eine Ortskoordinate hatten, die von minus bis plus unendlich lief:

Von Karl Hilpolt – Eigenes Werk, CC BY-SA 4.0, Link
Sieht ganz ähnlich aus, hier waren links unten und links oben aber die Nullunendlichkeiten und die Ortskoordinate war nicht ein Radius, der von Null bis unendlich läuft, sondern eine normale (kartesische) Koordinate zwischen minus und plus unendlich. Die Ähnlichkeit ist also nur scheinbar. (Und das zu verstehen, hat mich ne Weile gekostet, das wird nämlich nirgends erklärt, jedenfalls in keiner der Quellen, in die ich geguckt hatte.)
Bei unserem SL haben wir also auch ein auf der Spitze stehendes Quadrat, aber die Interpretation ist eine andere. In beiden Diagrammen ist rechts eine raumartige Unendlichkeit, aber die Spitze links ist im einen Diagramm ebenfalls bei raumartig unendlich, im SL-Diagramm ist sie an einem Punkt bei r=1. (Mehr dazu später.) Die linke obere Seite des Diagramms ist im einen Fall die zukünftige Nullunendlichkeit, im anderen Fall der Ereignishorizont. Also bei solchen Diagrammen immer genau hinschauen, damit ihr nicht in die Irre geführt werdet -achtet auf die i’s und scri’s. (Sorry für’s falsche Apostroph, aber sonst sieht’s komisch aus.)
Schauen wir nochmal auf das SL-Diagramm. Die linke obere Seite ist der Ereignishorizont mit Koordinate r=1. Aber was ist die linke untere Seite? Hier ist auch r=1. Ist das auch ein Ereignishorizont?
In gewisser Weise ja – aber irgendwie auch nicht. Ihr seht anhand (easteregg: In meinem Buch in Kapitel 21 schreibe ich “an Hand” an einer Stelle getrennt, das hat einen sehr guten Grund, auch wenn es orthografisch nicht korrekt ist…) des Diagramms, dass es nicht möglich ist, Signale in diesen Ereignishorizont hinein zu schicken. Alle Signale aus Bereich 1 laufen ja maximal unter 45 Grad – die erreichen diese Linie also nie. Aber wenn ihr auf dieser Linie sitzen würdet, dann könntet ihr – wenn das Diagramm alles korrekt beschreibt – ohne Probleme ein Lichtsignal nach außen schicken; das läuft dann im Diagramm nach rechts oben und endet bei der Zukünftigen Nullunendlichkeit scri-plus. (Ich hoffe, solche abgefahrenen Begriffe schrecken euch jetzt nicht mehr…)
Die Linie links unten ist damit sozusagen die Umkehrung eines Schwarzen Lochs: nichts kann rein, aber alles, was da am Rand sitzt, kommt raus (außer einem Lichtsignal, das im Diagramm nach links oben ausgesandt wird, das friert genauso ein wie am Ereignishorizont des SL). Wir haben also kein Schwarzes Loch, sondern das Gegenteil: Ein Weißes Loch!
Wir können auch das Innere des Weißen Lochs einzeichnen, ganz symmetrisch. (Und damit alles noch symmetrischer wird, füge ich – bzw. Karl Hilpolt, an dieser Stelle mal ein herzliches Dankeschön für die schönen Bilder bei Wikimedia – links noch einen Bereich III ein, den erkläre ich gleich):
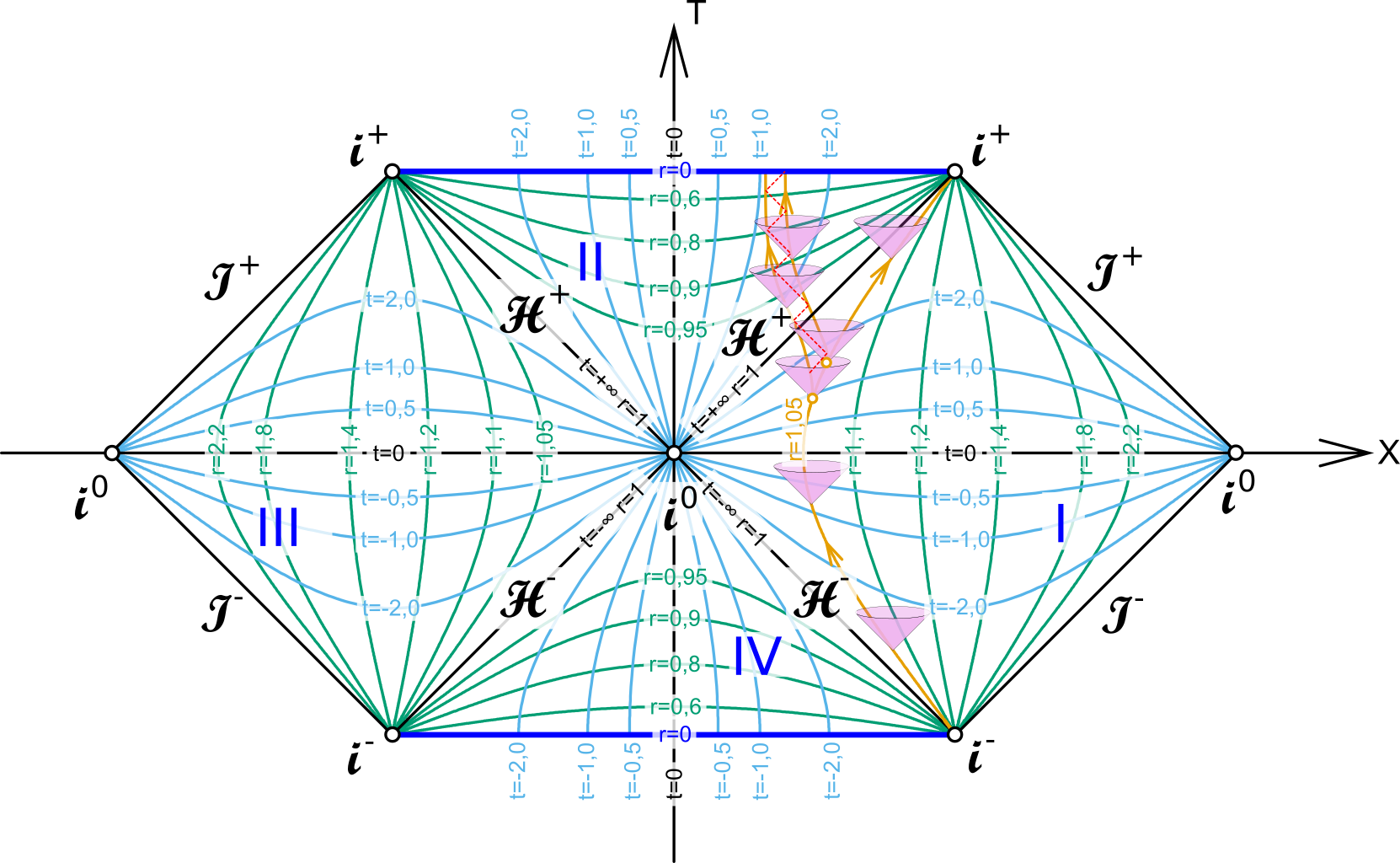
Von Karl Hilpolt – Eigenes Werk, CC BY-SA 4.0, Link
Wir haben jetzt ganz unten den Bereich IV, das Innere des “Weißen Lochs”. Unten ist die Singularität bei r=0; alles was aus diesem Bereich nach rechts fliegt und den Ereignishorizont rechts überquert, landet in Bereich I, also in unserem Universum. Alles was nach links fliegt, erreicht schließlich auch einen Ereignishorizont und landet im Bereich III. Bereich III ist, wie ihr sehen könnt, vollkommen symmetrisch zu Bereich I, mit diesem aber nicht verbunden (die beiden berühren sich genau in der Diagramm-Mitte). Bereich III ist also ein anderes Universum, nicht unseres.
Haben wir damit gezeigt, dass es ein Multiversum gibt – oder sonst wie andere Universen? Gemach, das haben wir nicht wirklich. Zunächst mal ist der Bereich III von unserem Universum vollkommen getrennt. Die beiden berühren sich in der Diagramm-Mitte, aber es ist unmöglich, von Bereich I nach III zu kommen, dazu müsstet ihr im Diagramm entlang einer Linie fliegen, die flacher als unter 45 Grad verläuft, und damit wärt ihr überlichtschnell. Überlichtgeschwindigkeit ist aber ja in der ART nicht möglich (jedenfalls nicht lokal, global kann man da schon ein paar Tricks aus Einsteins Hut zaubern…), also kommen wir auch nicht durch diese Verbindung zwischen den beiden Universum, es handelt sich um ein nicht passierbares Wurmloch. (Wenn ihr euch für passierbare Wurmlöcher interessiert, könnte ich da ein gutes Buch empfehlen…)
Hinzu kommt noch etwas anderes: bei dieser ganzen Konstruktion haben wir angenommen, dass unser SL schon immer existiert hat. In unserem Universum bilden sich Schwarze Löcher aber und sind nicht schon seit Ewigkeiten vorhanden. Was dann passiert, konstruieren wir beim nächsten Mal.
Vorher halten wir aber nochmal fest, dass wir damit das Penrose-Diagramm eines (seit Ewigkeiten existierenden, also statischen) SL konstruiert haben. Man erkennt den Ereignishorizont, sieht aus dem Diagramm eine Motivation für die Idee Weißer Löcher und bekommt einen ersten Eindruck, wie ein Wurmloch zwei Universen verbinden kann. Nicht schlecht für so ein Diagramm, oder?
Tja, es ist schon wieder passiert: Dieser Artikel wuchs und wuchs, während ich ihn schrieb, und den Kollaps eines SL (und sein Ende per Hawking-Strahlung) verschiebe ich auf einen dritten Teil…






Kommentare (43)