“Woher weiß man eigentlich, dass die kürzlich beobachteten Gravitationswellen von zwei kollidierenden schwarzen Löchern stammen? Diese Frage wurde mir in den letzten Tagen oft gestellt und die Antwort darauf führt in ein ziemlich interessantes Gebiet der Physik: Die numerische Relativitätstheorie. Es ist eine längere Geschichte, aber auch eine die zu erfahren sich lohnt.
Zwei schwarze Löcher verschmelzen. Aber woher weiß man das? (Bild: NASA/Ames Research Center/C. Henze”)
Theorie vs. Experiment
Es gibt ja zwei grundlegende Archetypen von Wissenschaftlern (zumindest laut den gängigen Klischees). Da sind einmal die genialen Theoretiker, die mit Papier und Bleistift in komplizierten Formeln revolutionäre Theorien über das Universum niederschreiben. Albert Einstein fällt sicherlich in diese Kategorie, aber auch moderne Physiker wie Stephen Hawking gehören zu diesen “Theorie-Genies”. Dann gibt es aber auch noch die genialen Bastler, die die seltsamsten Maschinen bauen und mit ihren Erfindungen die Welt verändern. Diese Art von Wissenschaftler findet man vor allem in den einschlägigen Kinofilmen; zum Beispiel Doc Brown aus “Zurück in die Zukunft”.

Das Genie schlechthin (Bild: Public Domain)
Die Realität sieht natürlich auch anders aus, aber im Wesentlichen ist die Trennung in die beiden Kategorien “Theoretiker” und “Experimentatoren” durchaus vorhanden. Beim kürzlich erfolgten ersten direkten Nachweise von Gravitationswellen konnte man die Rolle beider Disziplinen wunderbar beobachten. Da war natürlich der große Theoretiker Albert Einstein selbst, von dem die Vorhersage des Phänomens stammt. Aber auch viele, viele Theoretiker die ihm nachfolgten und seine Relativitätstheorie immer genauer verstanden um so immer besser zu verstehen, wie Gravitationswellen funktionieren. Aber ohne die ebenso vielen Techniker, Ingenieure und experimentellen Physiker wäre der Nachweis niemals gelungen. Eine Großforschungsanlage wie LIGO die an der Grenze des Mach- und Messbaren arbeitet, benötigt nicht nur hervorragende Theoretiker sondern eben auch erstklassige Leute, die in der Lage sind all das zu bauen. Ein Laserinterferometer mit einer Armlänge von 4 Kilometern; Technik die im Vakuum funktioniert; Spiegel die völlig erschütterungsfrei aufgehängt werden können, und so weiter.
Der Nachweis der Gravitationswellen war ein Triumph von Theorie und Experiment. In diesem Fall hat aber auch noch eine dritte Disziplin eine maßgebliche Rolle gespielt, die sich nicht so einfach dem theoretischen oder experimentellen Lager zuordnen lässt: Die Numerik.
Numerische Physik oder numerische Astronomie steht gewissermaßen zwischen den beiden Lagern. Sie basiert auf der Theorie, untersucht sie aber mit anderen Methoden. Wie in der Theorie wird in der Numerik die Mathematik zur Untersuchung eingesetzt, aber die Art und Weise wie man sie benutzt ähnelt eher der Vorgangsweise der experimentellen Physik. Es fällt mir (erstaunlich) schwer, die Disziplin der Numerik in einem Satz zu definieren. Ich probiere am besten, es am Beispiel meiner eigenen Arbeit als Wissenschaftler zu erklären. Mein Spezialgebiet ist die numerische Astronomie oder noch spezieller: die (numerische) Himmelsmechanik. Dabei geht es um die Untersuchung der Bewegung von Himmelskörpern wie Planeten, Asteroiden oder Sternen. Eine rein experimentell/beobachterischer Ansatz dieses Phänomens würde sich auf die Messung von zum Beispiel Planetenpositionen mit einem Teleskop beschränken. Eine rein theoretische Betrachtung würde sich mit den dieser Bewegung zugrunde liegenden mathematischen Gleichungen, zum Beispiel dem Newtonschen Gravitationsgesetz, beschäftigen.
Näherungsweise exakt
Die Numerik liegt irgendwo dazwischen. Und gerade die Astronomie ist ein gutes Beispiel um ihren Wert zu demonstrieren. Will man die Bewegung eines Planeten per Beobachtung untersuchen, kann das dauern. Himmelskörper wie Uranus oder Neptun brauchen Jahrhunderte für einem Umlauf um die Sonne; Sterne brauchen Jahrmillionen für einen Umlauf um das Zentrum der Milchstraße; Galaxien brauchen Jahrmilliarden um sich in ihren Galaxienhaufen zu bewegen, und so weiter. Alle Informationen nur durch reine Beobachtung zu erlangen ist unmöglich. Der theoretische Ansatz ist nicht viel besser. Wir kennen zwar die entsprechenden mathematischen Gleichungen, die die Bewegung von Planeten, Sternen und Galaxien beschreiben. Aber wir wissen auch, dass es unmöglich ist, diese Gleichungen exakt zu lösen. Was bleibt, ist die Numerik. Also Methoden, um die Gleichungen zumindest näherungsweise zu lösen.
“Gleichungen näherungsweise lösen” klingt einfach und vielleicht so, als müsste man sich dazu einfach nur nicht so viel Mühe geben. Ein bisschen schlampig sein; die Sachen schnell mal abschätzen; sich irgendetwas ausdenken oder so… Aber das hat mich echter Numerik überhaupt nichts zu tun! Wer das nicht glaubt, braucht sich nur mal kurz in eine Numerik-Vorlesung an der Universität setzen (oder ein einschlägiges Lehrbuch betrachten). Mathematische Methoden zu finden, mit der sich Gleichungen auf eine vernünftige Art näherungsweise lösen lassen sind nicht leicht zu finden. Es geht dabei ja nicht nur darum, einen möglichst geringen Fehler zu machen und dabei noch über die zu erwartende Größe des Fehlers Bescheid zu wissen. Das ganze soll dann auch noch anwendbar sein; die beste Methode nutzt nichts, wenn ihre Anwendung noch komplizierter ist als die normale Lösungsmethode. Es geht ja darum, etwas zu finden, was in der Praxis funktioniert!
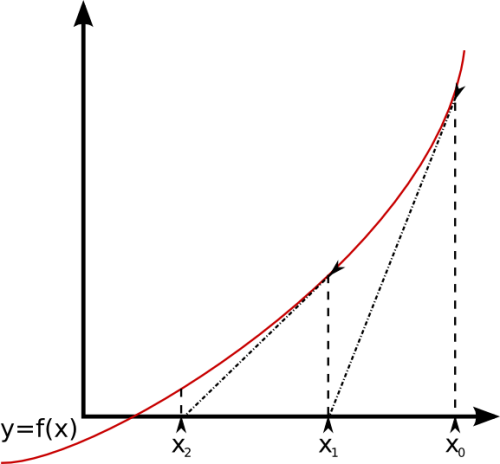
Die numerische Mathematik existiert schon seit Jahrhunderten; schon Isaac Newton hat Verfahren entwickelt, die heute immer noch zum Standardinventar gehören. Die meisten numerischen Methoden basieren auf Iterationsverfahren. Man ersetzt die eigentlich zu lösende Gleichung durch eine andere, die einfacher zu lösen ist. Die Lösung der vereinfachten Gleichung wird als Ausgangspunkt für eine neue Gleichung verwendet, die wieder gelöst wird, und so weiter. Je länger man diese Iteration treibt, desto kleiner wird der Unterschied zwischen der Näherungslösung und der “echten” Lösung. Früher war es mühsam, all das händisch zu rechnen und die nummerischen Verfahren waren notgedrungen nie so genau wie es eine exakte Lösung geworden wäre. Als es aber dann Computer gab, änderte sich die Situation!
Wenn man heute Bewegung von Himmelskörpern untersucht, nutzt man fast immer numerische Methoden. Es ist kein Problem mehr, die entsprechenden Gleichungen in einen Computer zu stecken und dort numerisch zu lösen. Man kann der Bewegung von Planeten, Sternen und Galaxien für Jahrmilliarden folgen, wenn man Lust und entsprechend viel Computerpower hat. Das hat dazu geführt, dass die rein theoretische Untersuchung der Bewegungsgleichungen in der Himmelsmechanik mittlerweile in den Hintergrund gedrängt wurde. Es ist heute viel einfacher, mal eben schnell den Rechner anzuwerfen, wenn man eine Frage zur Bewegung von Himmelskörpern hat, als sich mit den Gleichungen selbst herumzuschlagen (die ja sowieso nicht lösbar sondern nur mit der extrem kniffligen Störungsrechnung und anderen fiesen mathematischen Methoden halbwegs in den Griff zu kriegen sind). Natürlich ist es in der Realität nicht ganz so simpel, ein vernünftiges Programm zu schreiben, dass in der Lage ist, die Bewegung von Himmelskörpern zu berechnen. Da steckt viel Arbeit drin und meistens ist so ein Programm auch nur für den jeweiligen Spezialfall nutzbar; genau so wie ein Versuchsaufbau in der Physik im Allgemeinen nur für eine spezielle Fragestellung brauchbar ist. Genauso hat auch der rein theoretische Ansatz immer noch seinen Wert – aber das jetzt genau auszuführen würde jetzt zu weit führen.
Einsteins fiese Gleichungen
Denn eigentlich geht es ja um die numerische Relativität! Und die Allgemeine Relativitätstheorie hat das gleiche Problem wie die Himmelsmechanik; nur noch ein bisschen mehr. Die Einsteinschen Feldgleichungen sind extrem kompliziert. Diese Gleichungen beschreiben, wie Massen die Raumzeit krümmen und wie sich Objekte aufgrund dieser Krümmung durch den Raum bewegen. Man kann sie zwar mathematisch exakt lösen, aber nur unter sehr speziellen Bedingungen die dann ebenso spezielle Fälle beschreiben. Eigentlich will man aber die echte Raumzeit verstehen und das ist mit einem rein theoretischen Ansatz nicht möglich. Man muss numerische Lösungen finden und das hat sich in der Relativitätstheorie als richtig schwierig erwiesen.
Will man zum Beispiel wissen, was mit zwei schwarzen Löchern passiert, die einander immer näher und kommen und irgendwann verschmelzen, steckt die Antwort auf diese Frage in den Feldgleichungen. Sie direkt zu lösen ist aber zu schwer. Und sie numerisch zu lösen in diesem Fall ebenso. Die Numerik wird immer dann problematisch, wenn es um Singularitäten geht. Ein schwarzes Loch ist eine Singularität, aber damit sind allgemein Fälle gemeint, in denen irgendeine Größe Null oder Unendlich wird. Kollidiert zum Beispiel ein Asteroid mit einem Planeten, ist der Abstand zwischen beiden zum Zeitpunkt der Kollision gleich Null. Die Gravitationskraft zwischen ihnen berechnet sich laut Newton aus dem Kehrwert des Abstands und durch Null dividiert es sich eben sehr schlecht. In der Himmelsmechanik hat man Wege gefunden, damit umzugehen und es ist auch nicht so kritisch, wenn man nicht bis exakt zum Kollisionszeitpunkt rechnen kann. Ein Asteroid, der 5 Meter vor der Erdoberfläche steht wird nicht auf einmal umkehren und wieder wegfliegen…
Aber bei zwei schwarzen Löchern sind es gerade diese letzten Momente, die kritisch sind und wo die Dinge passieren, die wir verstehen wollen. Und bis man hier die passenden numerischen Methoden entwickelt hat, hat es überraschend lange gedauert. Erste Versuche, die Relativitätstheorie numerisch zu fassen, gab es schon in den 1960er Jahren. Damals war aber noch nicht mal wirklich klar, was schwarze Löcher überhaupt sind und Computer gab es in der heutigen Form ebenfalls noch nicht. Erst in den 1980er Jahren gab es Fortschritte – aber damals konnte man nur sehr spezielle Fälle untersuchen, in denen die Konfiguration der Begegnung schwarzer Löcher enorm symmetrisch war und nicht unbedingt dem entsprach, was in der Natur erwartet wird. In den nächsten Jahren entwickelte man dann verschiedene neue Ansätze, von denen man sich Erfolg versprach. Zum Beispiel die “Excision”: Dabei wird der störende Teil, also die Singularität quasi aus der Simulation “herausgeschnitten”. Da alles was hinter dem Ereignishorizont stattfindet sowieso keinen Einfluss auf den Rest haben kann, kann man es eigentlich auch ignorieren. Auch das klingt einfacher als es ist und es hat gedauert, bis man das so hinbekam, um vernünftige Lösungen zu erhalten. Ein anderer Ansatz, “Punctures” genannt, ersetzt die ursprünglichen Gleichungen durch einen rein mathematisch leicht zu lösenden Teil, der die Singularität enthält und einen Teil, der numerisch gelöst wird. Das hat aber nur funktioniert, wenn sich die Singularität nicht bewegt – was sie in der Realität bei der Kollision zweier schwarzer aber tut.
Es hat bis ins Jahr 2005 gedauert, bevor der südafrikanische Physiker Frans Pretorius eine Methode entwickelt hatte, mit der sich die komplette Kollision und Verschmelzung zweier schwarzer Löcher numerisch am Computer darstellen ließ (“Evolution of Binary Black Hole Spacetimes”). Er nutzte dafür eine Weiterentwicklung der Excision-Methode; nur wenige Monate später gelang es unabhängig zwei anderen internationalen Forschungsgruppen, auch die Punctures so anzuwenden, dass sie brauchbare Ergebnisse lieferten (Accurate Evolutions of Orbiting Black-Hole Binaries Without Excision”, “Gravitational wave extraction from an inspiraling configuration of merging black holes”).
Numerische Vorhersagen!
Jetzt war es möglich, genaue Vorhersagen der Gravitationswellen zu machen, die bei so einem Ereignis frei werden. Ohne diese Entwicklung wäre die kürzlich erfolgte Entdeckung am LIGO-Observatorium nicht möglich gewesen. Beziehungsweise: Sie wäre viel schwieriger gewesen. Denn es war ja Zufall, dass man gerade die Verschmelzung zweier schwarzer Löcher als erstes beobachtet hat. Es hätte auch irgendein anderes Ereignis sein können; zum Beispiel die Gravitationswellen einer Supernovaexplosion. Diese Wellen sind aber lang nicht so eindeutig vorhersagbar. Eine Supernova ist ein komplexes Ereignis, dessen exakter Verlauf immer noch nicht verstanden ist und es gibt auch keine exakten mathematischen Gleichungen die ihn beschreiben. Schwarze Löcher sind aber – rein mathematisch gesehen – recht simple Objekte. Sie haben eine Masse, einen Drehimpuls und eine elektrische Ladung und das war es auch schon wieder. Mehr Eigenschaften haben sie nicht und als man es dann geschafft hatte, die Feldgleichungen für diesen Fall numerisch zu lösen, konnte man sehr klare und eindeutige Vorhersagen machen.
Als man bei LIGO dann Signale registrierte, die genau diesen klaren und eindeutigen Vorhersagen entsprochen haben, war die Interpretation nicht schwer. Das, was LIGO beobachtet hatte, waren zwei schwarze Löcher, die miteinander kollidierten und dann verschmolzen. Und man konnte das deswegen so genau sagen, weil knapp 10 Jahre zuvor Numeriker herausgefunden hatten, wie man die Einsteinschen Feldgleichungen für solche Fälle am Computer lösen kann.
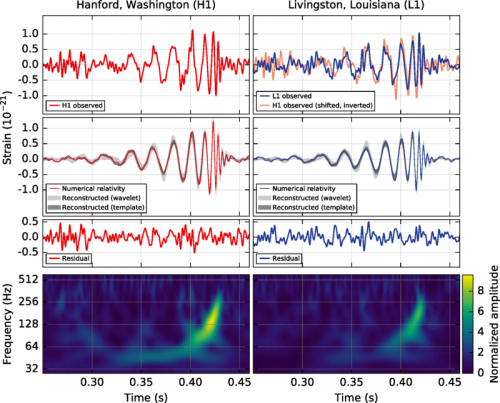
Genau so wie vorhergesagt: Die Beobachtung von Gravitationswellen bei LIGO (Bild: Abbott et al, 2016, CC-BY 3.0)
Wer mehr (und im mathematischen Detail) über die Geschichte der numerischen Relativitätstheorie Bescheid wissen, dem kann ich den Artikel “The numerical relativity breakthrough for binary black holes” von Ulrich Sperhake empfehlen.
Und wenn man diese ganze Entwicklung berücksichtigt, dann versteht man auch, wieso Albert Einstein vor knapp 100 Jahren so fest davon überzeugt war, dass niemand je Gravitationswellen nachweisen würde können. Supercomputer und die entsprechende numerische Methoden gab es damals noch nicht und selbst Visionäre wie Einstein hätten sie wohl nur schwer voraus sehen können. Von all den anderen technischen nötigen Fortschritten wie beispielsweise dem Laser mal ganz abgesehen…
Der Nachweis der Gravitationswellen war eine Gemeinschaftsleistung von Theorie und Experiment. Und der Numerik! Die steht zwar oft im Schatten der älteren wissenschaftlichen Disziplinen – gerade in diesem Fall lohnt es sich aber, sich genauer mit ihr zu beschäftigen.


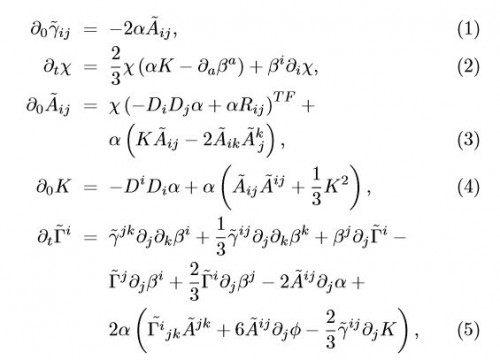











Kommentare (76)